基坑放坡开挖对下方既有地铁隧道影响计算及风险预测*

卜康正，郑先昌，沈 翔，刘继强，张万照

(1. 广州大学 土木工程学院，广东 广州 510006； 2. 中铁南方投资集团有限公司，广东 深圳 518052)

0 引言

随着城市快速发展，地下工程建设项目数量以及规模日益增大，在已建地铁隧道上方的基坑工程也越来越多。基坑开挖会引起下方既有地铁隧道隆起变形，隆起变形过大则会破坏隧道结构，甚至致使隧道管片破裂，管片接缝处出现漏水、漏泥现象[1-2]。为了确保已建地铁隧道的结构安全，深圳市《城市轨道交通安全保护区施工管理办法(暂行)》中，对邻近既有地铁隧道施工对其影响的量化指标行为做以下规定[3]：1)既有隧道结构绝对沉降量及水平位移量≤20 mm(包括各种加载和卸载的最终位移量)；2)既有隧道的相对变形曲率≤1/2 500(在既有地铁区间隧道上方实施大面积的加卸载工程中，该指标是极其关键的一个指导性技术指标)；3)由于建筑物垂直荷载(包括基础地下室)及降水、注浆等施工因素而引起的既有隧道附加荷载≤20 kPa。因此，研究基坑开挖对下方既有地铁隧道影响这一问题具有重要意义。

目前，学者主要通过数值模拟[4-6]和理论计算[7-9]2种方法研究基坑开挖对下方既有地铁隧道影响。其中，理论计算研究结果与实测值吻合良好，且相比于数值模拟研究，不需进行复杂的三维数值建模，因此更加简便。鉴于此，越来越多学者利用理论计算方法分析基坑开挖对下方既有地铁隧道影响[7-9]，即基于Mindlin应力解，推导得到矩形基坑开挖引起下方既有地铁隧道的附加荷载，并通过两阶段分析方法计算得到隧道位移和相对变形曲率。但在实际工程中，对于浅基坑因放坡开挖的经济适用性而常被采用，可目前尚未有学者针对放坡开挖基坑对下方既有地铁隧道影响提出有效的理论计算方法。

此外，由于土层参数的不确定性，隧道结构的安全风险尚需运用科学的方法预测。针对这一问题，徐耀德等[10]利用层次分析、模糊综合评价等方法，建立基坑工程与隧道各项因素下的风险判别矩阵，预测隧道结构的安全风险；陈大川等[11]通过熵权法完善风险判别矩阵各项因素的权重确定过程，使风险预测方法更加合理。但前人研究大多只能分析得到隧道最有可能发生某一等级的风险，未能计算得到隧道结构处于各级风险的概率，不利于工程人员根据隧道结构处于各级风险的大小制定完备的风险预防方案。因此，现有研究尚有不足，还需做进一步研究。

本文基于Mindlin应力解[12]，推导得到放坡开挖基坑引起下方既有地铁隧道的竖向和横向附加荷载，通过两阶段分析方法[7]，计算得到地铁隧道的竖向和横向位移，并基于正态分布概率模型对土层物理力学参数随机取值，利用蒙特卡罗方法对地铁隧道结构处于各级风险的概率进行计算，以期为基坑下方既有地铁隧道结构的安全评估提供参考。

1 基坑开挖引起隧道的竖向附加应力公式

设基坑坑顶的纵向边长为a，横向边长为b，深度为h，隧道埋深为z0，基坑与隧道位置关系如图1所示。

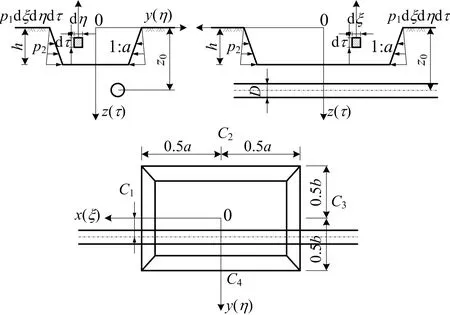
图1 基坑与隧道位置关系Fig.1 Position relationship of foundation pit and tunnel

由文献[13]可知，基坑开挖卸荷时，坑内土体存在残余应力，则坑内每一点土体竖向卸荷为p1=γ(1-λ)，利用Mindlin应力解，通过积分得到坑内全部土体竖向卸荷引起下方既有隧道轴线上的点(x,y0,z0)竖向附加应力为：

(1)

基坑开挖卸荷时，在基坑侧壁Cn(n=1,2,3,4)面产生水平三角形荷载p2=K0γτ，则p2引起隧道轴线上的点(x,y0,z0)竖向附加应力为：

(2)

式中：z3=z0-τ；z4=z0+τ；βn=(η,ξ,η,ξ)；Xn=(x-0.5a+ατ,y0+0.5b-ατ,x+0.5a+ατ,y0-0.5b-ατ)；

K0为坑壁外土的侧向土压力系数。

所以在坑内土体竖向卸荷和坑壁水平荷载的作用下，既有隧道轴线上任意一点(x,y0,z0)的竖向附加应力为：

(3)

利用高斯积分法求解σz中的定积分项，乘以隧道直径D，得到隧道轴线上各点的总竖向附加荷载集合Qz。通过两阶段分析方法[7]，并运用matlab编程计算得到隧道轴线上各点的竖向位移和相对变形曲率集合Uz。

2 基坑开挖引起隧道的横向附加应力公式

坑内全部土体竖向卸荷引起隧道轴线上点(x,y0,z0)的横向附加应力为：

(4)

式中：y01=y0-η。

基坑侧壁C1、C3面水平三角形荷载引起隧道上点(x,y0,z0)的横向附加应力为：

(5)

式中：X1,3=±x-0.5a+ατ。

基坑侧壁C2，C4面水平三角形荷载引起隧道上点(x,y0,z0)的横向附加应力为：

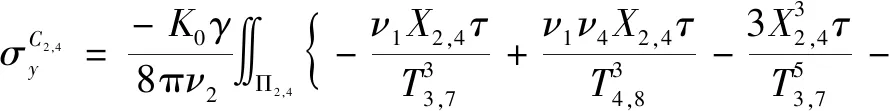
(6)

式中：X2,4=y0±(0.5b-ατ)；ν4=5-4ν；ν5=3-2ν。

所以在坑内土体竖向卸荷和坑壁水平荷载的作用下，地铁隧道轴线上任意一点(x,y0,z0)产生的横向附加应力为：

(7)

通过第1节的方法，得到隧道轴线上各点的总横向附加荷载集合Qy、以及横向位移和相对变形曲率集合Uy。

3 算例对比验证

算例一：上海市某基坑工程[7,11]，坑顶纵向边长a为240 m，横向边长b为230 m，开挖平均深度h约为7 m，基坑放坡坡度α为0。地铁1号线隧道位于基坑斜下方，上、下行线均平行于基坑纵向侧边，埋深均为14.9 m。隧道直径D均为6.2 m。其中，下行线隧道轴线在基坑侧边以外6.5 m处，上行线隧道轴线在基坑侧边以外20.5 m处，纵向抗弯刚度EI为1.26×108kN·m2。各土层物理力学参数取值可参考文献[7,14]。两阶段分析方法求解所需要的隧道所在土层竖向基床系数kz可根据Vesic公式[15]计算，即：

(8)

式中：Es为土的压缩模量。

两阶段分析方法求解所需要的隧道所在土层横向基床系数ky可根据式(9)[16]求得：

ky=φ·Es

(9)

式中：φ为横向基床系数的比例系数，可根据文献[17]中得到。

本算例竖向基床系数kz的计算结果为4.18×103kN/m2，横向基床系数ky的计算结果为6.0×103kN/m2。

将本文理论计算结果与实测值、文献[7]方法的理论计算结果进行对比，结果如图2所示，竖向位移以隧道隆起为正，横向位移以隧道向基坑内侧移动为正，下同。由于文献[7]未提出横向位移的计算方法，且文献[14]未给出上行线横向位移实测数据，因此本文只将下行线横向位移计算结果与实测数据作对比。

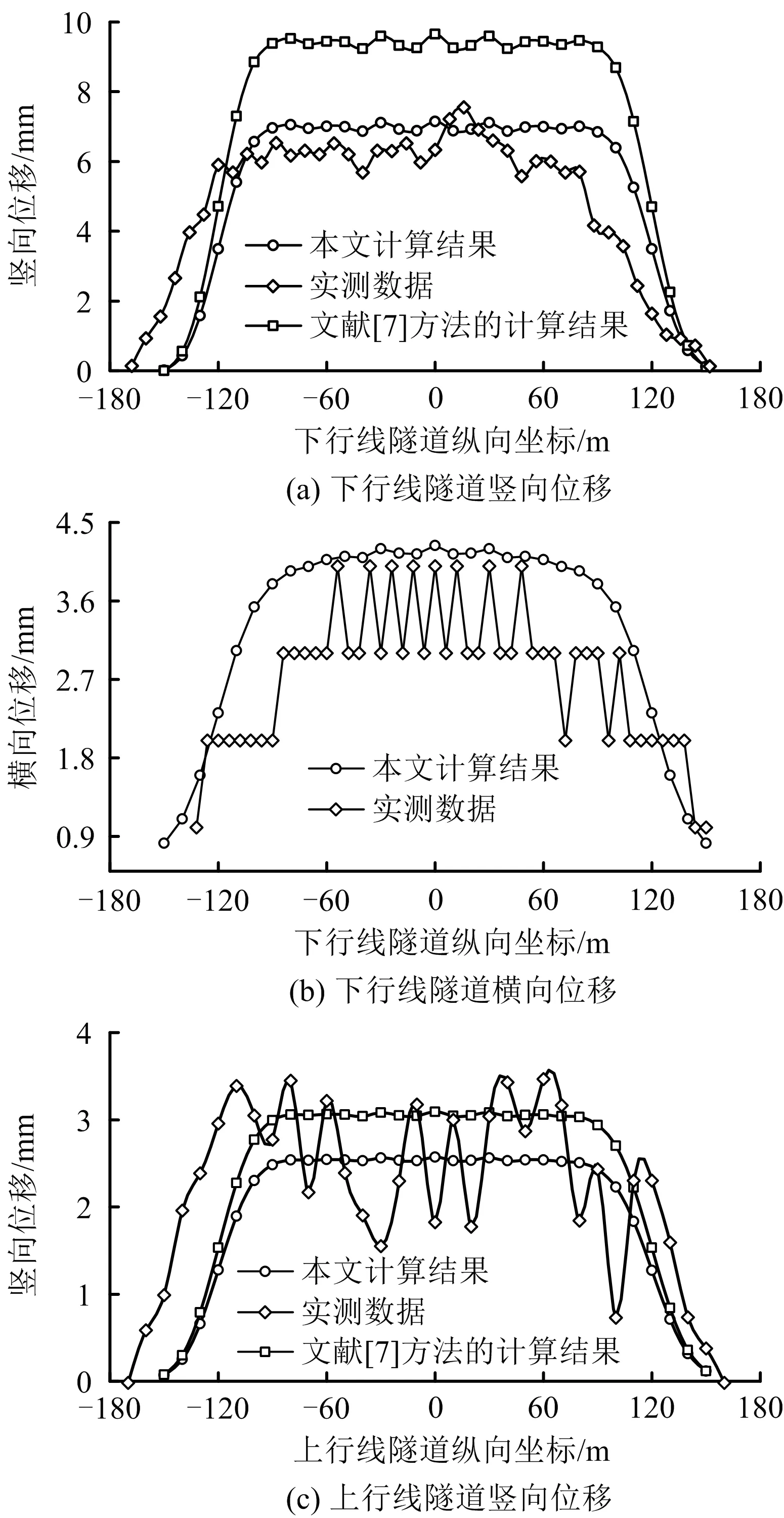
图2 计算结果对比Fig.2 Comparison of calculation results

由图2(a)可知，相比于文献[7]对下行线隧道竖向位移的理论计算结果，本文的理论计算结果与实测数据更为吻合，原因是本文计算坑内土体竖向卸荷引起隧道的附加荷载时，考虑到坑内土体是被多次分小块开挖完的，竖向卸荷的作用位置应在坑内土体原位置。而文献[7]却假设坑内全部土体被一次性开挖完，未作任何等效的情况下直接将竖向卸荷的作用位置移动至坑底，这与实际情况不符。因此，本文对下行线隧道竖向位移的理论计算方法更加符合实际工程；由图2(b)可知，本文的下行线隧道横向位移理论计算结果略大于实测数据，计算结果偏于安全，总体上可用于隧道的安全评估；由图2(c)可知，上行线隧道竖向位移实测数据波动较大，且本文和文献[7]的理论计算结果曲线虽与实测数据曲线总体趋势相同，但数值吻合度不高，原因是上行线隧道位于上海市共和新路与共和新路高架桥正下方，极易受到地面行车荷载和小范围道路改造工程的影响，而且邻近基坑开挖引起上行线隧道竖向位移数值较小，造成上行线隧道竖向位移数值在邻近基坑开挖、地面行车荷载和小范围道路改造工程3者共同影响下出现较大波动的情况。同时表明本文理论计算方法仍存在一定的局限性，不可用于道路正下方的隧道。

4 风险预测

在实际工程中，各土层物理力学参数并非如算例一[7]中的定量，而是在一定数值范围内的随机变量，因此，有必要根据土层物理力学参数的不确定性预测隧道结构处于各级风险的概率：根据隧道结构安全物理表现因子的量化指标的预警值、报警值、控制值对风险进行分级，计算各级风险发生的概率。

4.1 风险分级

根据《城市轨道交通地下工程建设风险管理规范》[18]第4.3节，隧道结构安全的风险可分为4个等级，本文选取隧道竖向和横向附加荷载、位移以及相对变形曲率共2类、6个隧道结构安全物理表现因子的量化指标的预警值(0.6倍控制值)、报警值(0.8倍控制值)、控制值作为分界点，具体取值如表1所示。由于本文研究的隧道附加荷载为沿隧道纵向的线荷载，因此还需乘以隧道直径D(下面算例二中D=6 m)，才能得到隧道附加荷载的各个分界值。

4.2 各级风险发生的概率计算

各土层物理力学参数包括基坑内土层的重度γ、泊松比ν1、静止土压力系数K0和隧道所在土层泊松比ν2、压缩模量Es，可在一定数值范围内的随机取值，且各取值出现的概率呈正态分布[21]。鉴于此，本文通过各土层物理力学参数对6个因子的敏感性分析，选取其中较为敏感的l个参数并对其取值进行随机抽样，利用蒙特卡罗方法[22]得到各级风险发生的概率。蒙特卡罗方法计算概率的步骤：

1)由于每个土层物理力学参数都服从正态分布概率模型，因此采用matlab编程，每次在l个较为敏感的土层物理力学参数取值范围内随机产生l个数值，组成1组数据。进行m次随机抽取试验则有m组数据。

2)将每组数据代入各计算公式，取每组计算结果中隧道竖向和横向最大附加荷载、最大位移以及最大相对变形曲率共6个因子的最大值。

3)根据表1中6个因子量化指标的风险等级划分标准，对各组所取6个因子最大值的计算结果进行统计归类，得到6个因子各级风险的发生概率。

4.3 算例分析

算例二：深圳市某待开挖基坑工程，坑顶纵向边长a为111.6 m，横向边长b为66.2 m，开挖深度h为10 m，基坑放坡坡度α为1.5。地铁11号线下行线隧道位于基坑下方，隧道轴线在距离基坑中轴线8.5 m处，且平行于基坑中轴线。隧道埋深为15.75 m，直径D为6 m，纵向抗弯刚度EI为3.55×107kN·m2。

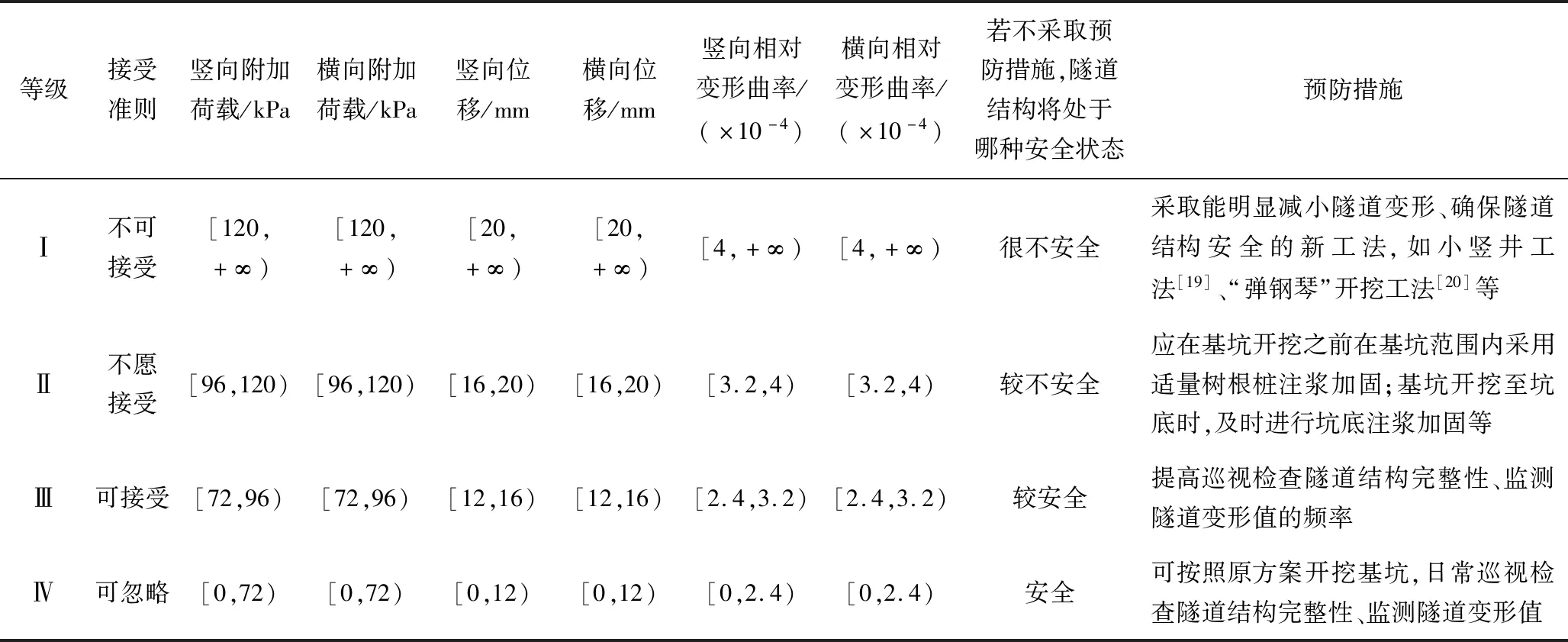
表1 不同因子的风险等级划分Table 1 Risk rank classification of different factors

各土层物理力学参数取值范围为：

1)基坑内土层

γ～N(19.1,0.812)(单位：kN/m3)；

ν1～N(0.33,0.0182)；

K0～N(0.45,0.0652)。

2)隧道所在土层

ν2～N(0.30,0.0072)；

Es～N(10.5,1.482)(单位：MPa)。

4.3.1 各土层物理力学参数对6个因子的敏感性分析

每次取其中一个土层物理力学参数变量的μ-2δ、μ-δ、μ、μ+δ、μ+2δ共5个数值进行敏感性分析，其他土层物理力学参数取值均为μ。则各土层物理力学参数对6个因子的敏感性分析结果如图3所示，μ为平均值，δ为标准差。

由图3可知：1)附加荷载对γ数值的改变最敏感；2)位移和相对变形曲率对Es数值的改变最敏感；3)附加荷载、位移和相对变形曲率对ν2数值改变的敏感性很低，因此为了减少各级风险发生概率计算结果趋于稳定时所需随机抽取试验次数，本文只选取敏感性相对较高参数γ、ν1、K0、Es的取值进行随机抽取试验，ν2取值恒为平均值，即0.30。

图3 各土层物理力学参数对6个因子的敏感性分析Fig.3 Sensitivity analysis of various physics and mechanics parameters of soil layers to six factors

4.3.2 不同因子各级风险发生的概率计算结果分析

如图4所示，当m=300时，不同因子各级风险发生的概率计算结果趋于稳定。因此，可以取此时的计算结果进行分析。

对不同因子各级风险发生的概率计算结果进行统计，统计结果如表2所示。

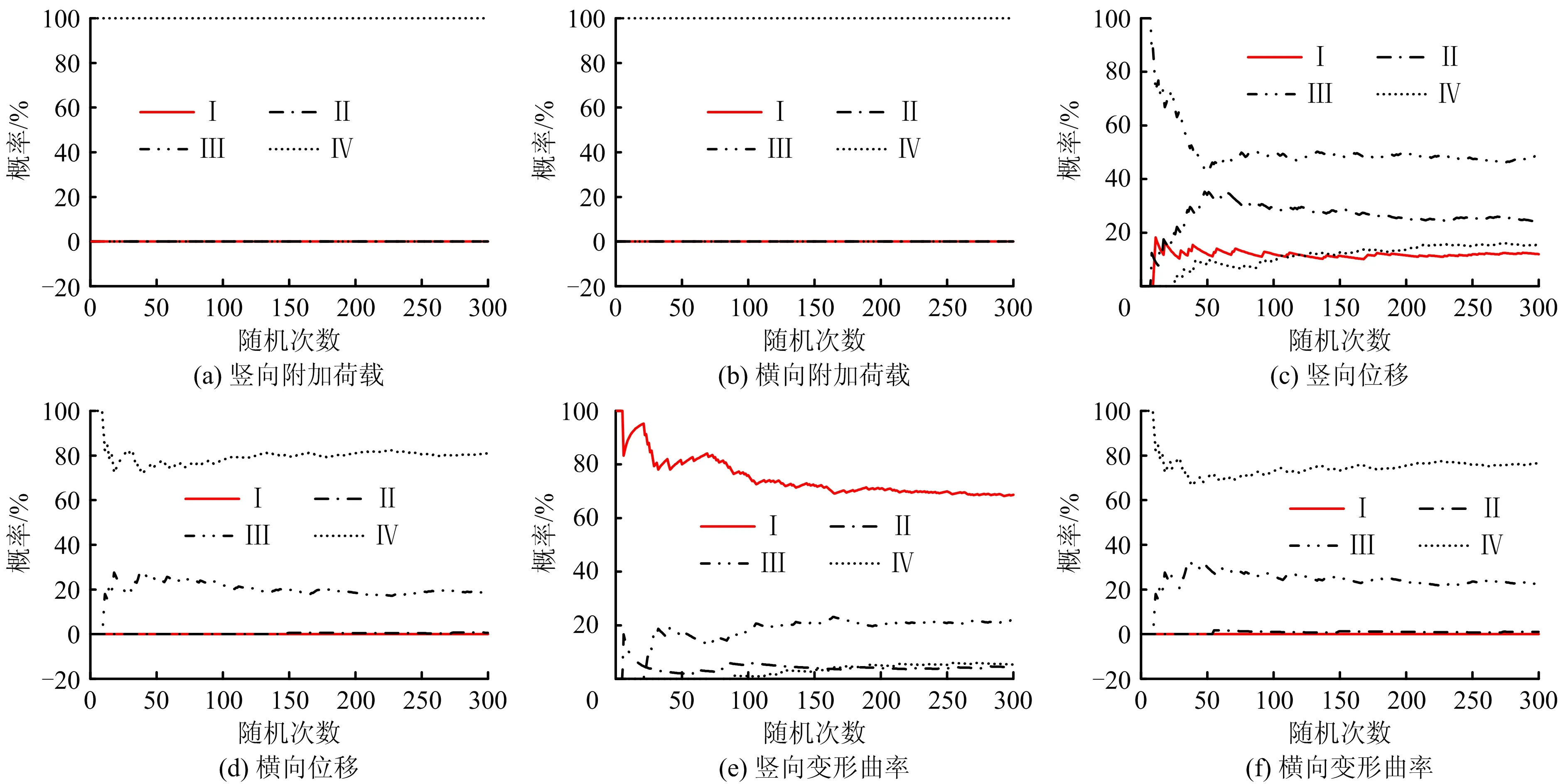
图4 不同因子各级风险发生的概率计算结果Fig.4 Calculation results of risk occurrence probability at different levels of different factors

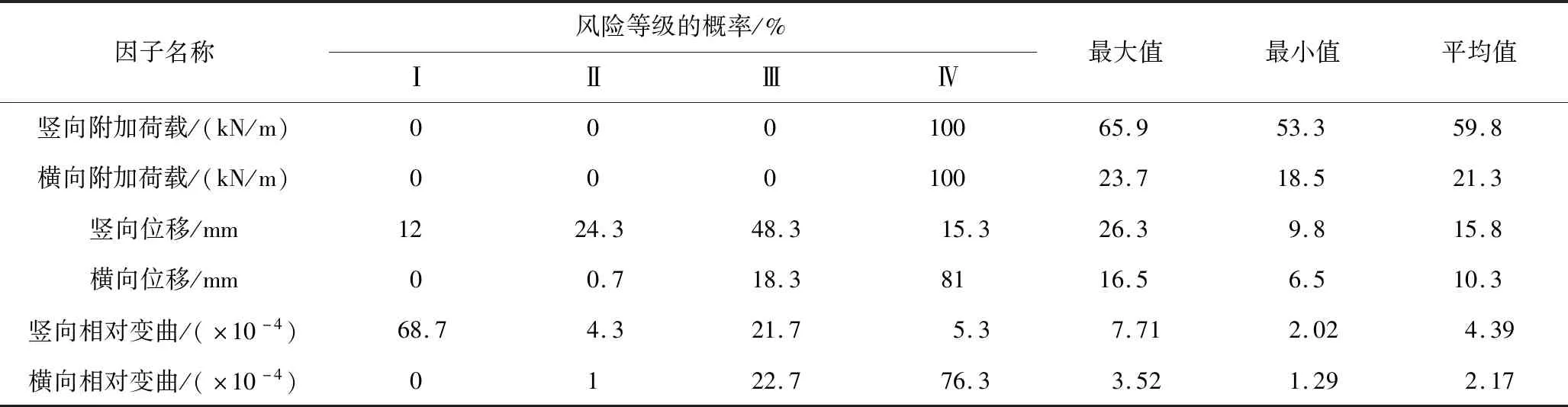
因子名称风险等级的概率/%ⅠⅡⅢⅣ最大值最小值平均值竖向附加荷载/(kN/m)00010065.953.359.8横向附加荷载/(kN/m)00010023.718.521.3竖向位移/mm1224.348.315.326.39.815.8横向位移/mm00.718.38116.56.510.3竖向相对变曲/(×10-4)68.74.321.75.37.712.024.39横向相对变曲/(×10-4)0122.776.33.521.292.17

由表2可知，基坑放坡开挖卸荷后，1)隧道竖向和横向附加荷载最大值分别为65.9，23.7 kPa，最小值分别为53.3，18.5 kPa，超过控制值的概率均为0，表明不采取预防措施的情况下，隧道管片不会因竖向或横向附加荷载过大而发生纵向或轴向开裂的情况；2)隧道竖向位移最大值为26.3 mm，最小值为9.8 mm，超过控制值的概率为12%，因此，必须采取适当的措施减小隧道竖向位移，避免隧道因竖向位移过大导致管片竖向错开，从而发生漏水、漏泥现象；3)隧道横向位移最大值分别为16.5 mm，最小值为6.5 mm，最大值并未超过控制值，说明隧道管片不会发生轴向错开现象；4)隧道竖向相对变形曲率最大值为7.71×10-4，最小值为2.02×10-4，超过控制值的概率高达68.7%。因此，必须采用能极大地减小隧道竖向相对变形曲率的开挖工法[19-20]，否则可能导致隧道管片纵向连接螺栓产生过度弯曲变形而失效，严重影响隧道结构的整体性和稳定性；5)隧道横向相对变形曲率最大值为3.52×10-4，最小值为1.29×10-4，最大值小于控制值。但竖向相对变形曲率超过控制值的概率较高，因此隧道管片轴向连接螺栓很可能不能发挥正常的连接作用。

4.3.3 竖向和横向2类因子综合影响下各级风险发生的总概率计算结果分析

图5 竖向和横向各因子的比值计算结果Fig.5 Ratio calculation results of different vertical and lateral factors

由图5可知，在100次随机试验中，竖向和横向2类因素中比值最大的因子总是相对变形曲率，表明在竖直和水平方向上对隧道结构安全造成最不利影响的因素始终是竖向和横向相对变形曲率，竖向和横向相对变形曲率各级风险发生的概率可分别作为竖向和横向两类因子各级风险发生的总概率。

由于竖向和横向2类因子计算公式互不关联、相互独立，则可由相互独立事件的总概率计算公式求出各级风险发生的总概率，即：

(10)

(11)

(12)

(13)

式中：P1，P2，P3，P4分别为Ⅰ，Ⅱ，Ⅲ，Ⅳ级风险发生的总概率；ri,j为第i个因子的j级风险发生的概率。各级风险发生的总概率计算结果如表3所示。

表3 各级风险发生的总概率计算结果Table 3 Calculation results of total probability for risk occurrence at different levels

由表3可知，隧道结构将处于不安全状态的总概率达到73.27%，处于很不安全状态的总概率甚至高达68.7%。因此，必须采取等级Ⅰ与Ⅱ中相应的预防措施，降低并管控各单因子的风险，至少将总风险降至等级Ⅲ(可接受)，然后实行等级Ⅲ中相应的预防措施，确保隧道结构安全。

5 结论

1)本文计算方法不仅适用于矩形开挖基坑(基坑放坡坡度为0)，而且可用于放坡开挖基坑，由于实际工程中往往会采用放坡开挖基坑，因此与原来仅限于矩形开挖基坑的计算方法相比，本文计算方法适用范围更广、实用性更强；计算坑内土体竖向卸荷引起隧道的附加荷载时，原计算方法假设坑内全部土体被一次性开挖完而直接将竖向卸荷的作用位置移动至坑底，但实际上坑内土体是被多次分小块开挖完，竖向卸荷的作用位置应在坑内土体原位置，本文计算方法以此为依据对原计算方法做了改进，因此与实际工程更为符合。

2)通过5个土层物理力学参数对各因子的敏感性分析，得到各因子较为敏感的4个参数γ、ν1、K0、Es。基于这4个参数取值的不确定性，利用蒙特卡罗方法预测算例二中隧道不同因子各级风险发生的概率。由风险预测结果可知基坑放坡开挖卸荷后，隧道竖向和横向附加荷载超过报警值的概率均为0，且隧道横向位移、横向相对变形曲率超过报警值的概率较低，仅为0.7%和1%，隧道结构因这4个因子处于不安全状态的可能性很低；隧道竖向位移和竖向相对变形曲率超过报警值的概率分别为36.3%和73%，并分别有12%和68.7%的概率超过控制值。因此，必须采取相应的措施减小隧道竖向位移和竖向相对变形曲率，避免隧道结构处于不安全状态；隧道竖向相对变形曲率是隧道结构处于不安全状态的最主要因子。

3)由竖向和横向2类因子综合影响分析可知，竖向和横向相对变形曲率分别为竖向和横向2类因子中表征隧道结构安全最具代表性的因子。隧道结构将处于不安全状态的总概率达到73.27%，其中，将处于不可接受风险(很不安全状态)的总概率高达68.7%。因此，必须采取相应的预防措施，降低并管控各单因子的风险，至少将总风险降至可接受水平。