风电机组偏航系统静态偏差分析与研究

徐金晖，郭鹏，宋鹏，柳玉

(1.华北电力大学 控制与计算机工程学院，北京 102206；2. 华北电力科学研究院有限责任公司，北京 100045)

0 引言

风力发电具有可再生及无污染的优势，过去的几十年里在全世界范围内得到了快速发展。随着风电机组装机容量的不断增大，对机组的控制系统与状态监测系统提出了更高的要求[1-2]。

偏航系统是风电机组的重要组成部分，它是使风电机组快速高效地完成对风操作，减少风电机组功率损失的执行机构[3]。由于风电机组运行工况复杂，偏航系统受偏航控制策略及系统误差的影响，常存在偏航误差，机组叶轮始终无法与来流风垂直。这样不仅会造成风电机组风能捕获效率降低，还会引起叶片气动弹性波动，增加机组的非对称载荷，影响机组的使用寿命[4-7]。

偏航误差主要包括控制策略引起的偏差以及偏航系统静态偏差。关于前者，相关学者提出了基于风向预测、分风速段、寻优算法、偏航系数等方法[8-12]，通过优化偏航控制策略来减小偏航误差。关于消除偏航系统静态偏差，文献[13]提出使用机载式激光雷达测风仪对风电机组偏航系统进行纠错，可有效减少偏航误差；文献[14]提出考虑风速变化的分段优化方法，并使用激光雷达测风仪数据，建立真实来流风向和机舱风向标测量风向的传递函数来补偿偏航静差，但激光测风仪成本较高，仅少量新型大容量风电机组有配备，上述方法并不适用于所有风电机组。文献[15]根据动量-叶素理论来计算风轮处轴向和切向速度诱导因子，并根据三角函数关系修正因叶轮尾流导致的风向标测量误差。文献[16]提出了一种基于功率曲线的偏航静差分析方法，将风速及偏航误差区间化处理，通过对比每个区间的功率特性来分析偏航静差所在区间，验证结果表明该方法能够有效地分析偏航静差。对于不配备激光雷达测风仪的风电机组，上述研究可有效地提高风电机组的发电效率。

本文针对目前风电场缺少激光雷达测风仪的现状，提出了改进区间化偏航系统静态偏差分析和计算方法。采用叶尖速比水平分布风速段的运行数据，减少控制因素对分析偏航静差的影响。量化分析各偏航误差范围内的功率特性，并提出偏航静差估计值的计算方法，以提高分析偏航静差的准确性。

1 实际运行中偏航静差来源

偏航误差为真实风向与机舱轴线之间的夹角，现场通常将风向标的零度基准与机舱轴线对准，因此，当风向标测量精准无误时，风向标测量的物理量就是偏航误差。由于风电机组运行环境恶劣，长期未检定的风向标往往存在测量误差。此时风向标测得的偏航误差与真实的偏航误差存在较大的差别，将此测量误差定义为偏航系统静态偏差。图1为偏航系统静态偏差示意图(图中：α为风向标测量的偏航误差；φ为真实的偏航误差；θ为偏航静差)。

图1 偏航系统静态偏差示意

Fig.1 Static deviation of yaw system

实际运行中，偏航静差的来源主要分为2种：(1)由于机组风向标的零度不再对准机舱轴线，导致风向标测得的偏航误差角度偏离真实值；(2)风电机组运行时，叶轮旋转会带动叶轮附近上下游的空气旋转，形成叶轮尾流，导致风向标测得的偏航误差与实际偏航误差存在一定的偏差，且这种偏差与叶轮转速相关，叶轮转速越大偏差越大。

2 偏航系统静态偏差分析方法

2.1 基于数据预处理的改进区间化偏航系统静态偏差分析方法

由于成本较高，绝大多数风电机组都没有配备激光雷达测风仪。对于这部分机组，根据运行数据来分析机组偏航系统静态偏差是简便有效的方法。

风电机组功率的表达式为

(1)

式中：P为风电机组的输出功率，kW；ρ为空气密度，kg/m3；Cp(λ，β)为风能利用系数；λ为叶尖速比；β为桨距角；A为风轮扫掠面积，m2；v为风速，m/s；φ为偏航误差。

由式(1)可知，风电机组的功率与偏航误差的余弦的3次方成正比。偏航误差的绝对值越大，风电机组的发电功率越小，功率损失越大。当偏航误差达到10°时，功率损失为4.48%，当偏航误差达到15°时，功率损失为9.87%。若风电机组的偏航系统存在静态偏差，偏航系统将始终不能正确完成对风操作。始终存在偏航误差，这就意味着风电机组会因偏航系统静态偏差的存在而造成更多的功率损失。当偏航误差为0°时，真实风向与机舱轴线的夹角为0°，此时风能利用率最大，机组功率性能最优。若偏航系统存在静态偏差，则此时风向标测得的偏航误差角度应偏离0°。若风电机组功率性能最优时风向标测得的角度为x，则角度x即为风电机组偏航静差。根据上述思路，按以下步骤对偏航静差进行分析。

2.1.1 数据预处理

选择用于分析偏航静差的变量为风向标测量的偏航误差α、风电机组输出功率P、叶片桨距角β和风速v。

首先，去除功率为0的停机数据以及风电机组工作在非正常状态下的数据。由于风电机组在额定风速以上会进行变桨恒功率控制，因此本文仅对额定风速以下的运行数据进行研究。当风速低于额定风速时，叶片桨距角应处在0°位置，所以叶片桨距角不为0°的数据也被去除。

其次，由于风电机组的功率特性不仅受偏航系统的影响，还受控制系统的影响，所以在挑选数据时需尽量减少控制因素对功率性能的影响。叶尖速比λ是机组叶片转速和风速的比值，是风电机组控制系统的重要参数。当叶尖速比变化较大时，对风电机组输出功率有较大影响。

(2)

式中：R为叶轮半径；ω为叶轮转速。

图2为某2 MW风电机组叶尖速比随风速变化的趋势图。从图2可以看出，当风速在6.0～8.0 m/s的区间时，叶尖速比呈水平分布。在该区间，风电机组处在最大风能追踪控制模式，机组的叶尖速比变化较小。因此，选取风电机组叶尖速比水平分布的风速区间内的运行数据进行分析，能够较好地排除风电机组控制系统参数波动对输出功率的影响。

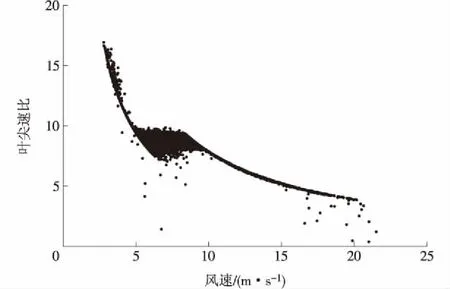
图2 叶尖速比随风速变化曲线

Fig.2 Curve of tip speed ratio changing with wind speed

2.1.2 偏航系统静态偏差分析方法

将风向标测量的偏航误差α和风速v进行区间化处理。将经过预处理的数据集按照风速分成5个区间，每个区间的范围如式(3)所示。

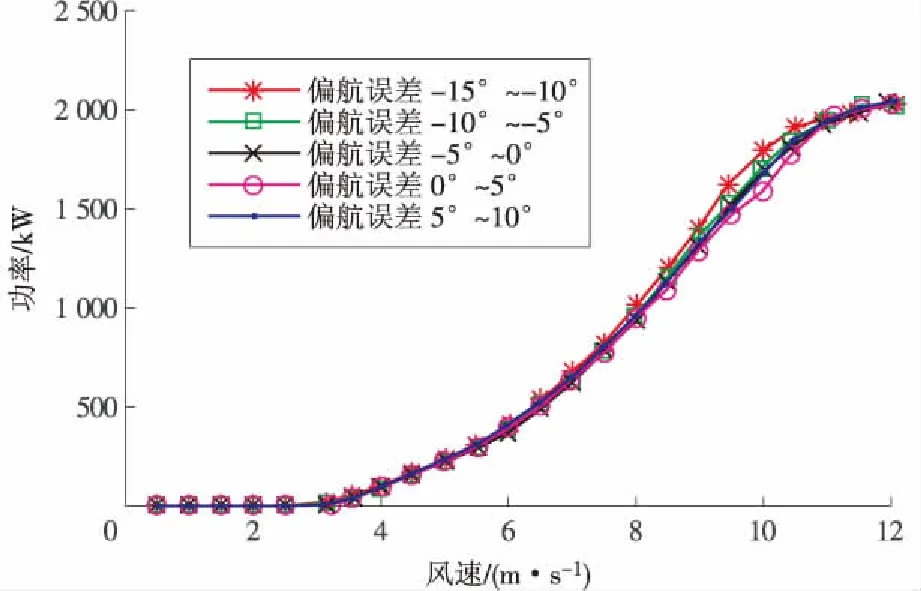
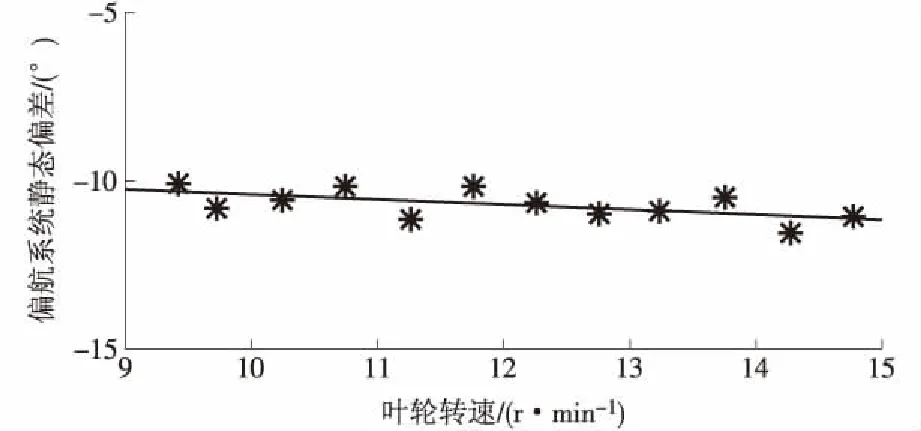
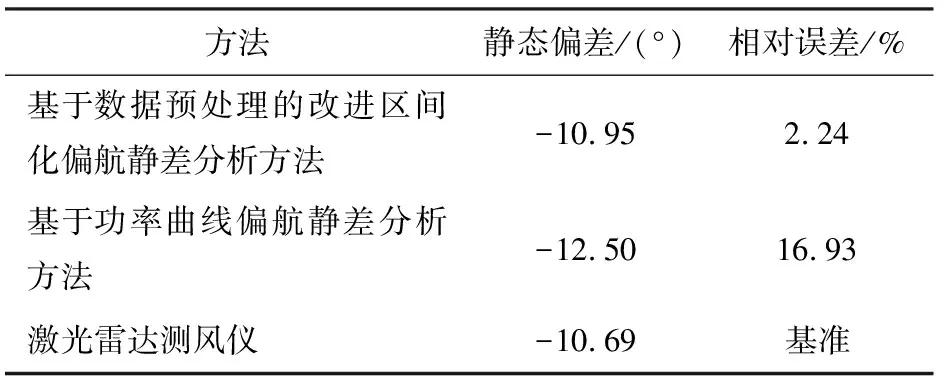
BIN(i)={Pv(i),αv(i)|v(i)

(3)

式中：v(i)为第i个区间的风速下限；v(i+1)为第i个区间的风速上限；每个区间的步长为0.4 m/s。

这样，每个区间内的数据都拥有相近的风速。由于所选运行数据的叶尖速比处在水平分布的范围内，在此风速范围内的每个区间，控制系统对机组功率的影响很小，可以近似认为功率P只受偏航误差角度α的影响。

为了更加精确地分析每个风速区间内功率与偏航误差的关系，进一步将每个风速区间按照偏航误差从-16°～16°划分为16个子区间，如式(4)所示。

式中：α(j)为第j个子区间的偏航误差下限；α(j+1)为第j个子区间的偏航误差上限；每个区间的步长为2°。

划分好区间后，计算每个偏航误差子区间内功率的平均值，作为衡量各子区间对应的功率性能指标。将每个风速区间内对应范围相同的偏航误差子区间的功率性能指标求和，求得的最大指标和对应的偏航误差子区间的范围即为偏航静差值的估计区间，计算公式如下

(5)

Pij=mean(P(v(i),α(j))) ，

(6)

式中：n为风速区间的数量；Pij为每个偏航误差子区间内功率的平均值。

以偏航误差为横坐标，以功率为纵坐标，计算各子区间对应的Pij并将其绘制出来，如图3所示。

图3 不同风速段内功率随偏航误差变化曲线

Fig.3 Curve of power changing with deviation of yawsystem in different wind speed intervals

计算出最大功率指标和对应的偏航误差范围后，选取该范围内所有数据的偏航误差的均值作为偏航系统静态偏差的估计值θe，如式(7)所示。

(7)

αij=mean(α(v(i),α(j))) ，

(8)

式中：αij为每个子区间内偏航误差的平均值。

改进区间化偏航静差分析方法流程如图4所示。

2.2 基于功率曲线的偏航系统静态偏差分析方法

将文献[16]中的基于功率曲线绘制的偏航系统静态偏差方法与本文方法进行比对分析。该方法的步骤为：对数据按照偏航误差进行区间化处理，将偏航误差从-15 °～10 °分为5个区间，每个区间步长为5 °；然后将每个偏航误差区间按风速0 ～13 m/s分为26个子区间，每个子区间步长为0.5 m/s；分别计算每个子区间内的平均功率。

以风速为横坐标，以功率为纵坐标，画出每个偏航误差区间对应的功率曲线，如图5所示。

3 案例分析

3.1 激光雷达测风仪数据分析偏航系统静态偏差

本文数据来自河北省张家口市坝上高原地区的风电场，该风电场场地开阔平坦，海拔为1 280～1 600 m。该风电机组为2.0 MW、水平轴、变桨、变速、双馈型机组，叶轮直径为93 m，轮毂高度为80 m。机舱式激光雷达测风仪安装在风电机组机舱上方，利用多普勒频移原理，可测量风速、风向等多种风资源风况参数，其测量范围为10～300 m(竖向与横向)，测量精度高。以激光雷达数据分析得到的偏航静差为基准，来验证2.1章节中基于数据预处理的改进区间化偏航静差分析方法的精确性。

图5中位于最上方的功率曲线所对应的偏航误差区间即为偏航静差值的估计区间，取该区间的中位数作为偏航静差值的估计值。

图4 基于数据预处理的改进区间化偏航静差分析方法流程

Fig.4 Flow of improved interval yaw static analysismethod based on data preprocessing

图5 不同偏航误差区间内功率随风速变化曲线

Fig.5 Curve of power changing with wind speed indifferent yaw error intervals

本文采用的激光雷达数据为真实风向及机舱轴线之间的夹角，即真实的偏航误差φ，它与风电机组风向标测量的偏航误差α之间的差值θ即为偏航系统的静态偏差。

将静态偏差θ按照叶轮转速分区，每个叶轮转速区间的步长为0.5 r/min，计算每个叶轮转速区间内的θ及叶轮转速ω的平均值。以θ的均值为纵坐标，ω的均值为横坐标，在坐标系中画出θ及ω的散点并将这些散点拟合，得到一条拟合直线y=ax+b(y为偏航系统静态偏差；x为风电机组叶轮转速)，如图6所示。通过该直线可分析风向标偏航静差的组成：直线的斜率反映了偏航系统静态偏差随叶轮转速的变化，而直线的截距为风电机组风向标的校准误差。

图6 偏航系统静态偏差与叶轮转速的关系

Fig.6 Relationship between static deviation ofyaw system and impeller speed

本文采用该风电场#12风电机组2015年10月19日到11月2日的运行数据及安装在机舱上方的激光雷达测风仪的数据对偏航系统静态偏差进行分析。针对该试验机组激光雷达测风仪数据，分析静态偏差与叶轮转速之间的关系，得到拟合直线的公式为

y=-0.15x-8.89 。

(9)

可以看出，该风电机组的偏航静差受叶轮转速的影响较小。分析运行数据可发现，叶轮转速大部分处于[9.5 ，14.5] r/min的区间内，根据式(9)计算得到偏航静差的范围为[-10.31°,-11.07°]，取该区间中点值-10.69°。

3.2 用运行数据分析偏航系统静态偏差

用2.1章节中基于数据预处理的改进区间化偏航静差分析方法计算图3中不同偏航误差范围对应的功率指标，见表1。

表1 图3中不同偏航误差范围内对应的功率指标Tab.1 Corresponding power indicators with different yaw error intervals in figure 3

表1中最大功率指标对应的偏航误差区间为[-12°，-10°)，根据式(7)计算偏航系统静态偏差的估计值θe为-10.95°。

用2.2章节中基于功率曲线的偏航静差分析方法分析得到位于最上方的功率曲线对应的偏航误差区间为[-15°,-10°)，取区间中点-12.50°作为该方法偏航静差的估计值。

将上述结果与激光雷达测风仪数据分析所得结果进行比较，见表2。

表2 不同方法所得结果及误差Tab.2 Results and errors obtained by different methods

从表2可以看出，基于数据预处理的改进区间化偏航静差分析方法选择了叶尖速比水平分布风速段内的运行数据，由于减小了控制系统对功率的影响而凸现了偏航误差对功率输出的影响，与激光雷达测风仪测得的偏航静态误差结果更加接近。该案例表明，本文提出的方法能够根据风电机组运行数据准确地分析和计算偏航系统静态偏差。

采用激光雷达测风仪数据可分析得到偏航静差随叶轮转速变化的函数关系，当风电机组拆除激光雷达测风仪后，可根据叶轮转速的变化对偏航系统静态偏差进行补偿，进一步提高偏航系统静态偏差计算的准确性。

4 结束语

目前，由于激光测风仪的成本较高，无法安装到每台风电机组，而采用激光测风仪对风电机组风向标进行定期检定时，工作量大且无法实时发现偏航系统静态偏差的变化。本文提出了改进区间化偏航系统静态偏差分析和计算方法，采用风电机组控制系统参数(叶尖速比)水平分布风速段的运行数据，以减小控制系统对输出功率的影响。采用风速分区和偏航误差分区的方法来量化确定最大功率指标对应的偏航误差范围，并以该范围内偏航误差的均值作为偏航系统静态偏差的估算值。通过与基于功率曲线的偏航系统静态偏差分析方法以及激光测风仪数据进行比对分析，本文方法具有更高的准确性。该方法根据风电机组运行数据即可对偏航系统静态偏差进行准确的分析和计算，并可指导风电场运维人员及时进行修正和处理，对提高风电场的运维水平和经济效益具有重要的意义。