塔式太阳能电站三轴定日镜装置研究

徐 骥，杜 蕙，周 洪，方彦军

塔式太阳能电站三轴定日镜装置研究

徐 骥，杜 蕙，周 洪，方彦军

（武汉大学电气与自动化学院，湖北 武汉 4 30072）

针对现有塔式太阳能定日镜装置在极端天气下稳定性差的问题，本文提出采用三轴支撑方式的定日镜装置，通过有限元分析方法确定了3个支撑轴最优位置，根据地理位置和时间推算太阳的高度角和方位角，结合反射定律得到控制定日镜平面的最佳空间角度。在优化布置支撑轴的基础上，对支撑轴的高度控制量进行推导计算，并设计了相应的定日镜控制系统。最后，以某塔式太阳能电站实际数据为例进行试验验证，结果表明本文提出的定日镜控制系统正确可行。

塔式太阳能电站；光热发电；定日镜；运动控制；有限元分析；反射定律；太阳相对位置

随着温室气体排放带来的全球气候变化，以及新兴经济体的工业化进程加速发展，全球资源供给和环境承载压力日益突出，在能源需求总量增长的同时，世界能源结构正在发生变化[1]。太阳能因其资源充足、分布广泛、技术可靠等优点，成为一种理想的清洁能源[2]，太阳能有光热转换和光电转换2种利用形式，塔式太阳能发电是较理想的光热发电方式之一[3]。

现有的塔式太阳能发电系统中采用的定日镜多为双轴结构，主要由反射镜、基座、镜架、传动装置和定日镜角度控制系统组成[4]。通过互相正交的2个轴来控制定日镜的角度变化，以此来实现跟踪太阳方位，并将太阳光线投射至吸收塔顶部的目的。双轴控制能较好地完成定日跟踪，且控制算法实现简单。但其不足在于只能通过镜片中部的横向支撑轴来控制镜片的运动和偏转，支点在镜片中心，如遇天气状况恶劣或者风力较大时，容易发生振动甚至倾覆事故[5]。

与双轴方式相比，对定日镜装置采用合理布置的三轴支撑方式，从力学角度来说减小了单根支撑轴所需要承受的应力，能够提高定日镜装置面对极端天气时的稳定性。文献[6]提出了一种三轴支撑的定日镜装置，但对三轴定日镜具体的定日跟踪控制方法未详细描述。

对此，本文提出一种针对三轴支撑定日镜的控制策略，将定日镜镜面旋转角度的变化转换为对 3个支撑轴高度的控制，提高了定日镜的稳定性能，从而间接提高了塔式太阳能光热电站的发电效率。

1 三轴定日镜结构

塔式太阳能光热电站通过控制追踪太阳轨迹的定日镜场，将辐射能汇聚到中心吸热塔的接收器上，加热管道中的传热介质，从而产生高温蒸汽驱动汽轮机转动，进而将太阳能转变为电能[6]。图1为塔式太阳能光热电站的系统结构。

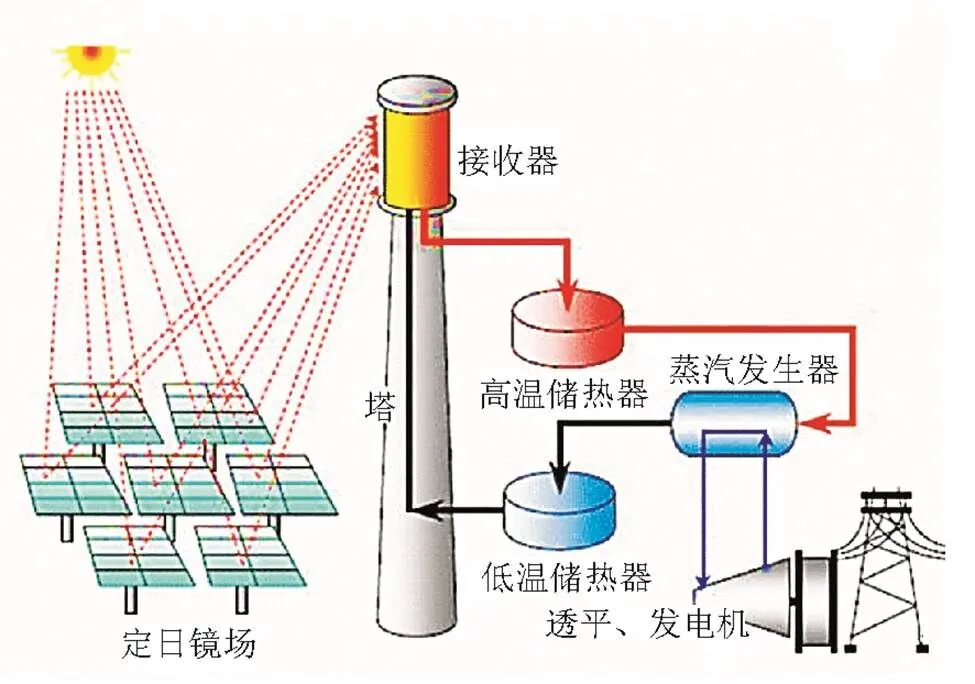
图1 塔式太阳能光热电站系统结构

1.1 三轴定日镜模型

图2为三轴支撑式定日镜模型[6]。定日镜背面与3个支撑轴分别啮合。步进电机通过啮合齿轮带动滚珠丝杆转动，从而调节支撑杆高度，3根支撑轴可独立工作。反射镜与3根支撑轴均通过万向节连接，每个连接点均满足3个方向的旋转自由度。

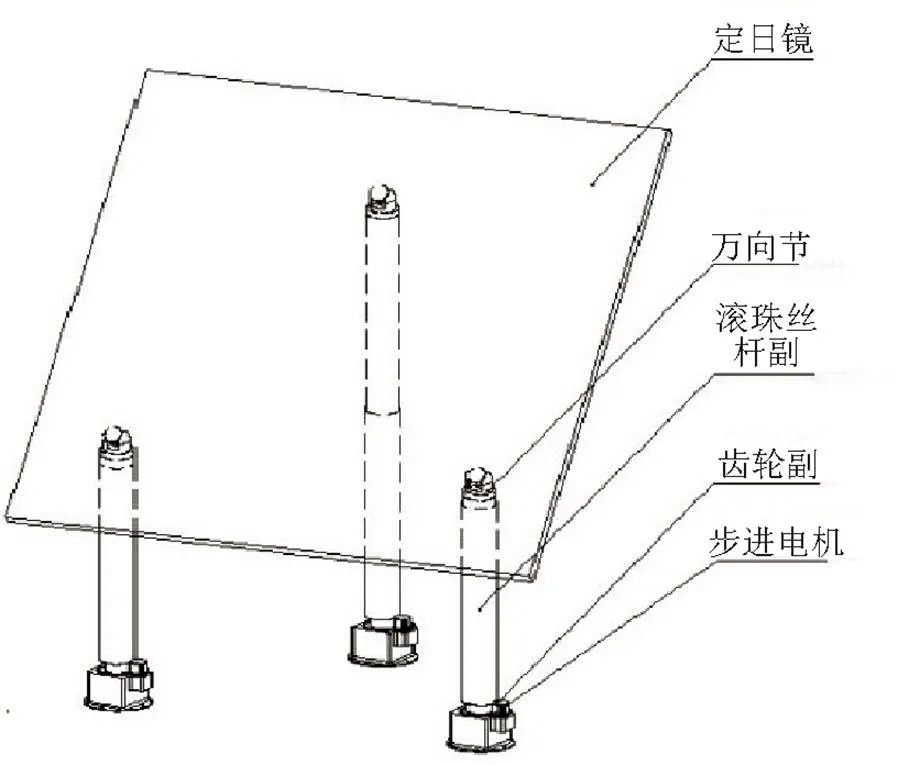
图2 三轴支撑式定日镜模型

1.2 三轴布置方式

对于三轴定日镜而言，3根支撑轴位置的布置十分关键。寻找三轴受力最均匀，所受合力较小的位置能够延长支撑轴的使用寿命，减少长时间工作造成的累积误差，使控制效果更加稳定。

有限元分析（finite element analysis，FEA）利用数学近似方法对真实物理系统（几何和载荷工况）进行模拟。利用FEA可以进行3种支撑方式的支撑轴受力情况的定性对比，从而得到不同方式支撑轴的受力情况，进而综合各因素选择对支撑轴损耗较小的方式。3种典型的矩形镜面支撑轴布置方式如图3所示，其中箭头线段表示的距离相等， 3种方式的定日镜尺寸、材质参数完全相同。

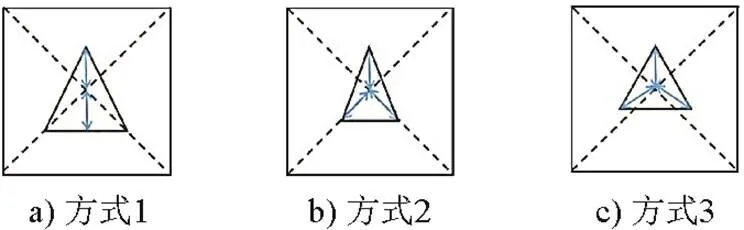
图3 3种典型的矩形镜面支撑轴布置方式

为了找到定日镜控制的最适合支撑方式，利用FEA软件进行3种支撑方式的支撑轴受力情况的定性对比。由分析结果可知：按照方式2布置的3根支撑轴，镜面板受到的应力基本集中在支撑轴附近，而镜面其他部位承受的应力较小，因此对镜面的损耗较小。故应选择方式2建立支撑轴。

2 太阳相对位置

由于地球和太阳以年为周期相对运动。因此可以根据月、日、时间、经纬度等信息计算给定时刻、给定地点的太阳位置。对地球上给定经纬度的地点，一般使用高度角和方位角计算太阳位置，而这2个参数可以根据太阳赤纬角和时角计算。太阳赤纬角是太阳直射光线即太阳与地球中心的连线和地球赤道平面之间的夹角，以年为周期变化。赤纬角计算公式[7]为

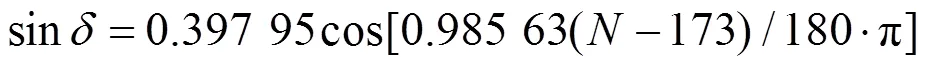
式中，为自1月1日起到计算日的天数。

太阳时角指观测点所在的天球子午圈到太阳所在时圈之间的角距离，一般用表示，

式中，R为真太阳时，即计算时的当地时间。假定观测地点维度为，则太阳的高度角s的正弦可表示为

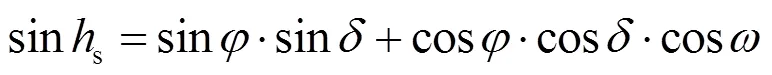
太阳方位角s的余弦可表示为

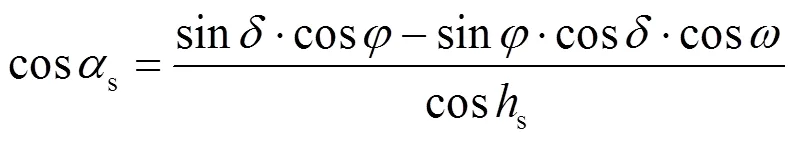
从而得到某时刻的太阳时角和赤纬角，再结合纬度信息，得到太阳位置的具体信息。

3 控制器给定值的确定

太阳能光热发电站镜场控制的目标是给定时间、地理位置等参数的条件下，使场中所有定日镜能够捕捉入射光并且将出射光线汇聚到集热塔的接收器上[8]。根据地理、时间信息确定单一定日镜的控制器给定值是控制问题的关键。

3.1 镜面角度

由反射定律可知，反射线、入射线和法线处于同一平面内，且出射光线和入射光线和法线的夹角相同。根据这一定理，需要定日镜将太阳直射光线全部反射到集热塔顶部，只需要知道定日镜的法线方程，即可确定定日镜的角度。法线方程可根据入射光线和出射光线之间的关系得到[9]。定日镜空间坐标系如图4所示。

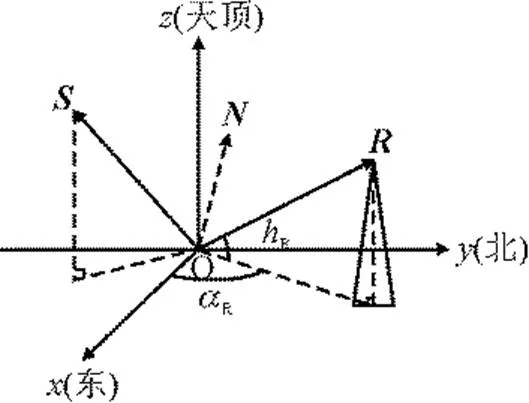
图4 定日镜空间坐标系

如图4所示，以定日镜的几何中心位置为原点，以该地正东方向为轴、正北方向为轴、天顶方向为轴建立空间坐标系，单位向量为太阳入射光向量的反向量，为从定日镜中心点到吸热塔顶部的出射光向量，为定日镜的法向量。

根据图4，3点的空间坐标可分别表示为(sss)、(nnn)、(rrr)。根据太阳和地球之间的位置关系，结合空间几何知识，推导出任意时刻太阳位置的计算公式，进而可以确定一定时间地点一天中不同时刻太阳的高度角和方位角。从而可用太阳高度角s和方位角s表示为

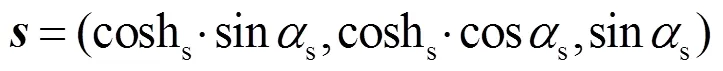
式中，s为集热塔相对定日镜的高度角，s为集热塔的位置角。

出射光方向根据集热塔相对镜面中心的位置确定。同样使用高度角和方位角，则可表示为

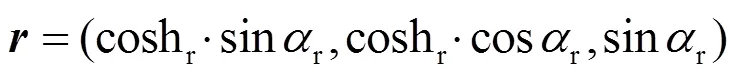
在太阳能电站镜场建成后，对每一面定日镜而言可视为固定参数。根据反射定理，入射光线的反向量和出射光线向量能够合成法向量，即

将式(5)和式(6)代入式(7)，即可得到单位法向量的表达式，根据法向量即可确定镜面角度。

3.2 三轴高度

根据1.2节三轴布置方式确定3个支撑轴，并从轴方向投影，3个支撑点在坐标系中的位置如图5所示。

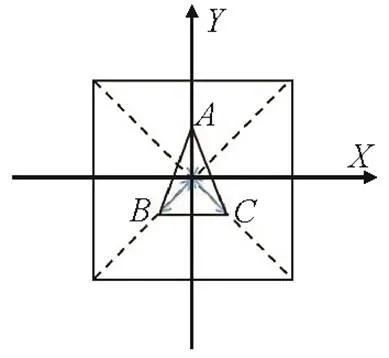
图5 定日镜z轴投影的坐标系

根据图5分析3点的几何关系，点的坐标为0，2点以轴对称。3个支撑点的坐标可分别表示为(0,a,a)、(b,b,b)和(–b,b,c)。根据法向量求取平面方程

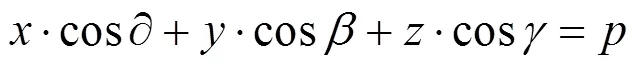
式中：cos、cos、cos为平面法向量，分别为与、、轴夹角的余弦；为坐标系中原点到平面的距离。由于法向量原点正好位于镜面上，因此=0。

将式(7)代入式(8)中，即可得到确切的定日镜平面方程。由于3点在定日镜背部位置固定，将3点的轴坐标代入式(8)可得到相应的轴坐标。由此可计算3点的轴坐标的表达式：

根据3点的轴坐标，可以知道3个支撑轴的相对高度，代入实际情况中可计算出三轴的具体高度，完成不同时刻对定日镜的角度控制。

4 定日镜控制系统

定日镜的控制采用程序控制为主、传感器控制为辅的方式。综合了程序控制稳定性好、计算量小和传感器控制精确性高的优势，能更好地完成对定日镜的控制[10]。定日镜控制系统结构如图6所示。

图6 定日镜控制系统结构

以年为尺度，太阳对于同一地点的运动变化规律几乎不变，因此根据第3节所述方法可以编程计算固定地点定日镜的角度。当输入日期、时间、经纬度等信息，可自动计算定日镜3个支撑轴的高度，根据高度数据对定日镜进行控制。同时，光线传感器对太阳的入射光线进行实时监测，收集偏差，信号转换后送入控制器处理，以此驱动定日镜角度的微调。当遇到多云或阴雨天时，切断传感器模块，只进行程序控制。根据气象数据，在日出30 min前，设置控制系统进入预备状态；在日落30 min后，设置控制系统停止工作，定日镜放平。传感器控制中，只有当偏差累积到一定数值，才反馈给可编程逻辑控制器（programmable logic controller，PLC）进行校正，使电机运转不过于频繁。总体程序控制流程如图7所示。

5 试验验证

选取某塔式太阳能发电站的实际数据进行 试验验证。该塔式太阳能发电站的经纬度为 E 97.803 267°，N 37.352 317°。选择2018年的夏至日6月21日为参考日期，根据第3节方法计算从太阳初升到日落每30 min的太阳高度角和方位角，结果见表1。

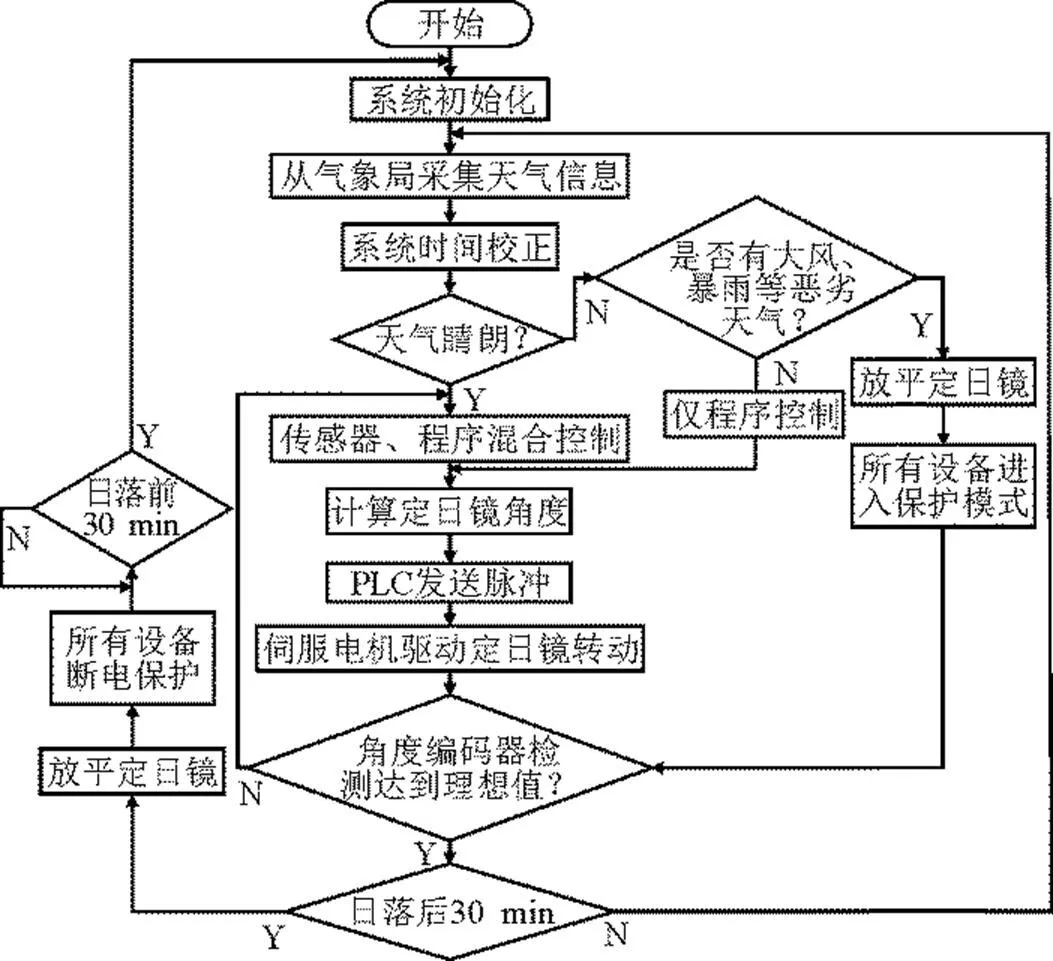
图7 总体程序控制流程

表1 某光热电站2018年夏至日太阳相对位置参数

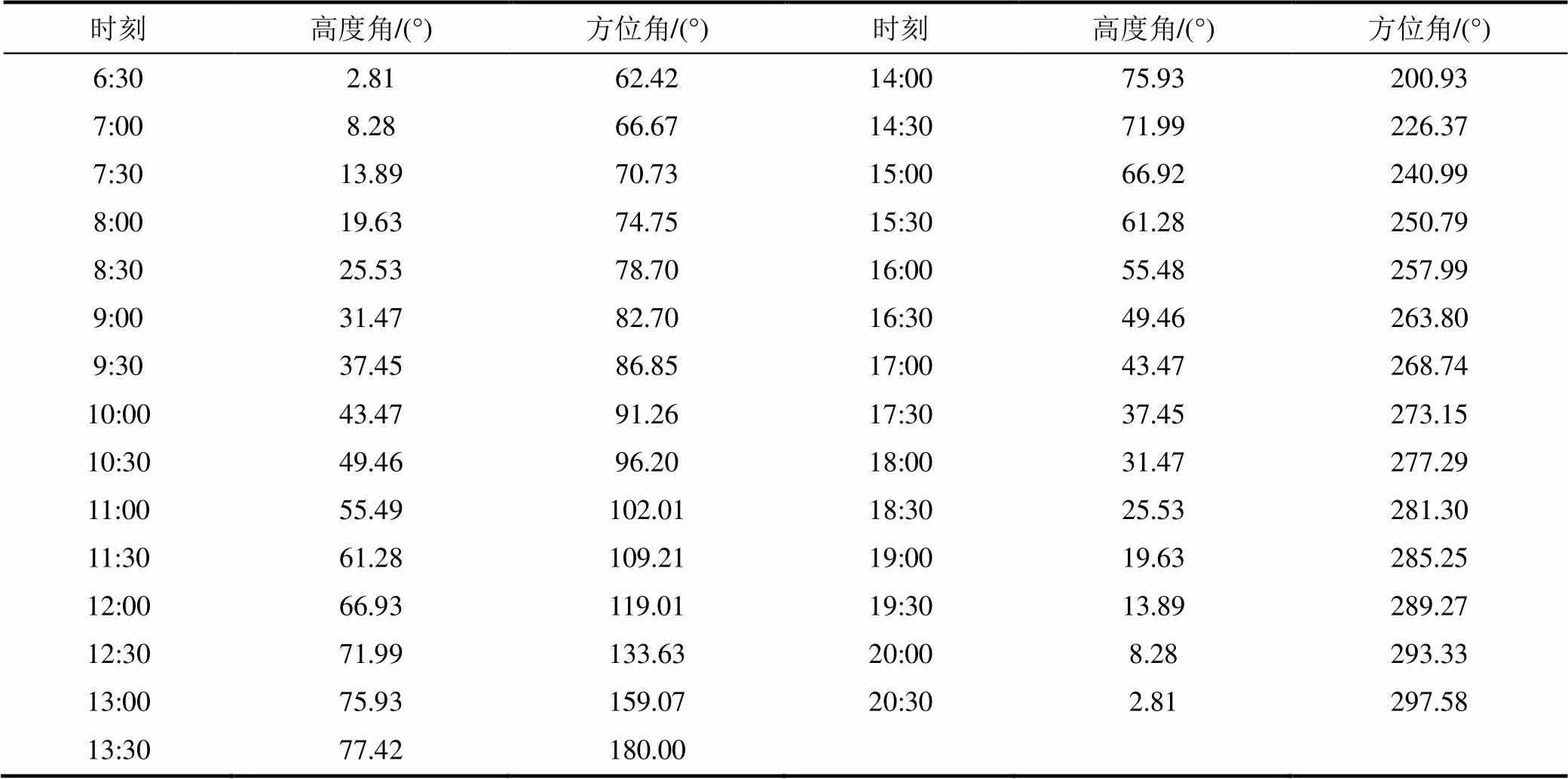
Tab.1 The relative sun position parameters of a photothermal power station on summer solstice, 2018

镜场中心集热塔高100 m，选取坐落于集热塔正南方向20 m处边长4 m正方形定日镜为研究对象。通过受力分析，选取平均受力最均匀的支撑轴布置方式，得到的最优布置为其支撑轴距离原点的俯视距离均为1 m。以定日镜原点为中心建立3.1节中图4所示单位长度为1 m的空间直角坐标系。则集热塔空间坐标为(0, 20, 100)，3个支撑轴坐标分别为(0, 1,a)、(–0.707, –0.707,b)、(0.707, –0.707,c)。根据第3节中计算方法可以得到3个支撑轴高度控制量的给定值（表2）。

表2 定日镜三轴夏至日内高度变化值

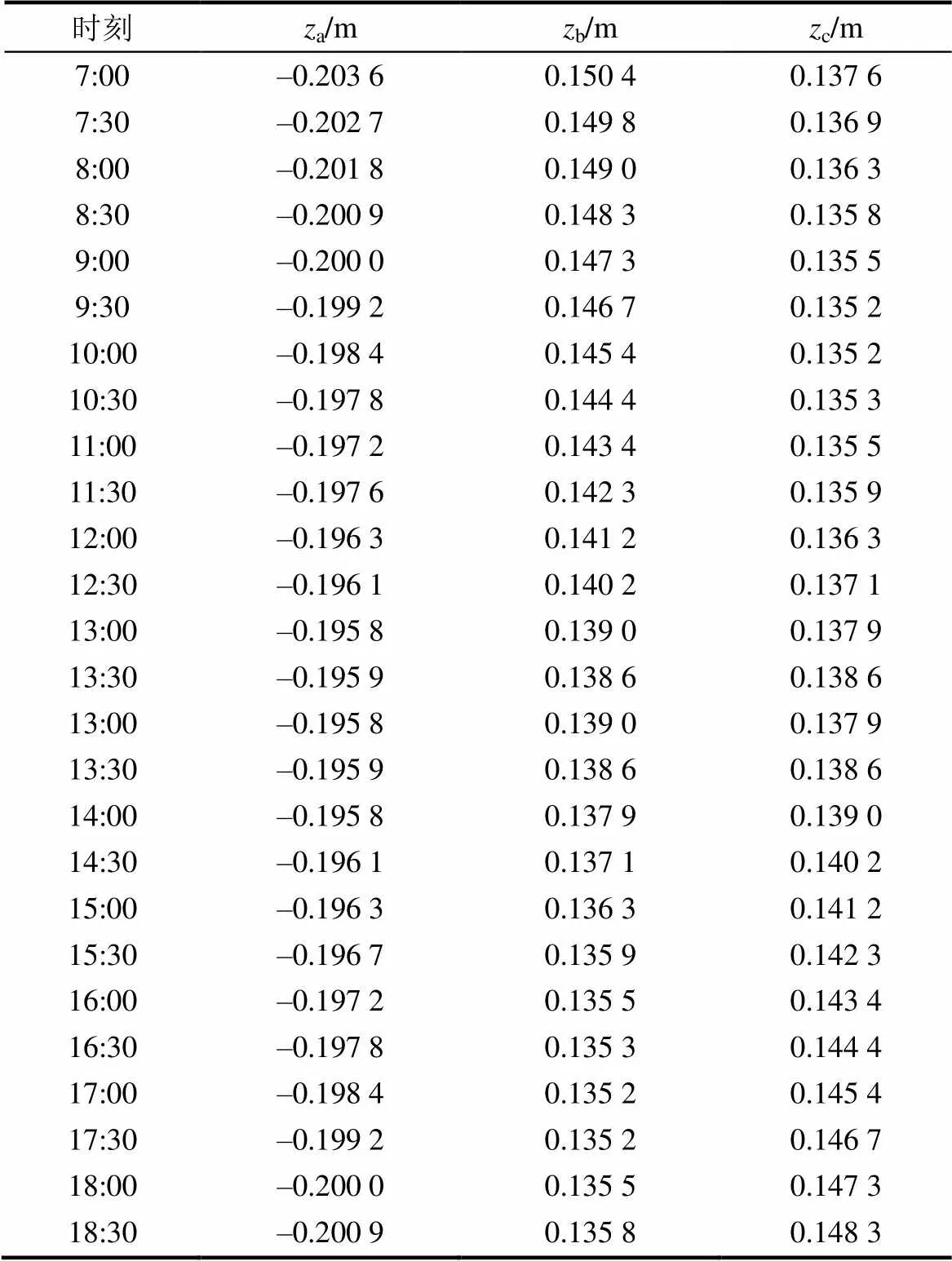
Tab.2 The change values of the three heliostat axes’ height on summer solstice, 2018

综合表1和表2数据可知，13:30时太阳处于日中，方位角为180°，此时太阳应处于坐标系的正南方（即轴负方向），由于集热塔位于正北方，故此时、2轴的高度应该相同。表2显示，此时b=c=0.138 6，符合推论。太阳方位角在10:00时接近90°，在17:00接近270°，由于对称性，这2个时间的高度应该相反。由表2可见，这2个时间段内(b,c)分别为(0.145 4, 0.135 2)和(0.135 2, 0.145 4)，符合推论。因此，本文所述的定日镜三维控制方法可行。

6 结 论

基于现有的双轴定日镜稳定性较差、易受极端天气影响的问题，本文提出一种三轴定日镜结构的控制方法，对支撑轴布置方式进行了优化，并在优化布置方式的基础上，分析了相应控制器给定值的计算方法，并且设计了相匹配的控制系统。以某塔式太阳能电站的实际数据为例，依照本文方法计算出一天内各个时刻定日镜3个支撑轴的相对高度。检验对比后发现所得结果符合实际情况，推导的三支撑轴高度计算方法成立，且准确性较高，证明了本文方法的可行性和正确性。

［1］ 周强, 汪宁渤, 何世恩, 等. 高弃风弃光背景下中国新能源发展总结及前景探究[J]. 电力系统保护与控制, 2017, 45(10): 146-154.ZHOU Qiang, WANG Ningbo, HE Shien, et al. Summary and prospect of China’s new energy development under the background of high abandoned new energy power[J]. Power System Protection and Control, 2017, 45(10): 146-154.

［2］ 蔡世杰. 太阳能利用技术研究现状及发展前景[J]. 中国高新科技, 2018, 33(21): 50-52. CAI Shijie. Research status and development prospect of solar energy utilization technology[J]. China High-Tech, 2018, 33(21): 50-52.

［3］ 李学来, 贺博. 太阳能光热电站发展展望[J]. 能源与环境, 2017(6): 75-77.LI Xuelai, HE Bo. Development prospect of solar thermal power station[J]. Energy and Environment, 2017(6): 75-77.

［4］ 郭铁铮. 塔式太阳能热发电站中的定日镜跟踪装置研制[J]. 中国电机工程学报, 2008, 28(35): 114-119. GUO Tiezheng. Development of heliostat tracking device in solar tower power plant[J]. Proceedings of the CSEE, 2008, 28(35): 114-119.

［5］ SUN H, BO G, QIANG Y. A review of wind loads on heliostats and trough collectors[J]. Renewable & Sustainable Energy Reviews, 2014, 32(5): 206-221.

［6］ 杨琛, 薛铮, 方彦军, 等. 塔式太阳能镜场三轴支撑定日镜控制装置[J]. 热力发电, 2018, 47(12): 35-40. YANG Chen, XUE Zheng, FANG Yanjun, et al. Three-axis support heliostat control device in tower solar energy mirror field[J]. Thermal Power Generation, 2018, 47(12): 35-40.

［7］ 曹传钊, 郑建涛, 刘明义, 等. 塔式太阳能热发电技术的发展[J]. 可再生能源, 2013, 31(12): 21-25. CAO Chuanzhao, ZHENG Jiantao, LIU Mingyi, et al. Development of tower solar thermal power generation technology[J]. Renewable Energy, 2013, 31(12): 21-25.

［8］ IGEL E A, HUGHES R L. Optical analysis of solar facility heliostats[J]. Solar Energy, 1979, 22(3): 283-295.

［9］ 祝雪妹, 宓霄凌, 黄文君, 等. 塔式太阳能电站中定日镜集群的追日控制[J]. 控制工程, 2017(6): 1131-1135. ZHU Xuemei, MI Xiaoling, HUANG Wenjun, et al. Sun-tracking control of heliostat clusters in solar tower power plant[J]. Control Engineering of China, 2017(6): 1131-1135.

［10］ 郝晓弘, 郭铁锷, 汪宁渤, 等.开-闭环结合控制方式的定日镜跟踪控制策略[J]. 自动化仪表, 2018, 39(9): 5-9. HAO Xiaohong, GUO Tiee, WANG Ningbo, et al. Tracking and controlling strategy of heliostat based on open-closed-loop control mode[J]. Process Automation Instrumentation, 2018, 39(9): 5-9.

Study on three-axis heliostats for solar-thermal power stations

XU Ji, DU Hui, ZHOU Hong, FANG Yanjun

(School of Electrical Engineering and Automation, Wuhan University, Wuhan 430072, China)

The existing heliostats have the disadvantage of poor stability in extreme weathers. To solve this problem, a three-axis supporting heliostats is proposed. The optimal positions of the three supporting poles are ascertained by using the finite element method. The height angle and azimuth angle of the sun are deduced according to the geographical position and time, and combining with the law of reflection, the optimum spatial angle for controlling the plane of the heliostats is obtained. Based on optimizing the arrangement of the position of the support shafts, the given value of the height control of the support shafts is deduced, and the corresponding control system is designed. Finally, by taking the actual data of a tower type solar-thermal power station as the example, the verification experiment is carried out, and the results show that the heliostats control system presented in this paper is correct and feasible.

tower solar power station, solar-thermal power generation, heliostats, motion control, finite element analysis, reflection law, relative position of the sun

TM615; TK513

A

10.19666/j.rlfd.201901035

徐骥, 杜蕙, 周洪, 等. 塔式太阳能电站三轴定日镜装置研究[J]. 热力发电, 2019, 48(7): 92-96. XU Ji, DU Hui, ZHOU Hong, et al. Study on three-axis heliostats for solar-thermal power stations[J]. Thermal Power Generation, 2019, 48(7): 92-96.

2019-01-13

国家自然科学基金项目(51807143)；中国博士后科学基金特别资助(2018T110797)；中国博士后科学基金面上项目(2017M612499)

Supported by：National Natural Science Foundation of China (51807143); China Postdoctoral Science Foundation Funded Project (2018T110797); General Project of China Postdoctoral Science Foundation (2017M612499)

徐骥(1987—)，男，博士研究生，主要研究方向为光伏发电技术，xuji1986@outlook.com。

周洪(1962—)，男，博士，教授，博士生导师，主要研究方向为智能电网与网络控制技术、发电与电网信息控制，hzhouwuhee@whu.edu.cn。

（责任编辑 杜亚勤）