基于太阳能颗粒集热的超临界CO2流化床换热器模拟研究

陈 博，倪明江，应振镇，岑可法，肖 刚

基于太阳能颗粒集热的超临界CO2流化床换热器模拟研究

陈 博，倪明江，应振镇，岑可法，肖 刚

（浙江大学能源工程学院，浙江 杭州 310027）

基于太阳能颗粒集热的超临界CO2布雷顿循环系统效率高，发展潜力巨大。本文应用更加精确的颗粒侧传热模型，构建了超临界CO2流化床换热器模型，以100 kW换热功率的换热器工况参数为基础，对传热管外径尺寸、管束数量、颗粒粒径和流化气体温度进行优化。结果表明：在满足CO2流动压损为0.01 MPa的条件下，优化后换热器的管束参数为管外径10 mm，壁厚2.9 mm，管束数量97根；选择小粒径颗粒时，临界流化速度较低、流量较小，可以有效降低气体热损失，提高换热器热效率和降低风机能耗，优化管束参数条件下，当颗粒粒径从100 μm增至500 μm时，气体热损失从70.32 W增至1 176.00 W，热效率从99.93%降至98.84%，风机能耗从21.60 W增至405.97 W；流化气体入口温度从570 ℃提高到630 ℃，换热器热效率从98.52%提升至99.64%。

太阳能光热发电；超临界CO2；流化床；换热器；热效率；压力损失；风机能耗

高参数动力循环是降低太阳能光热发电成本的重要途径。目前，太阳能光热电站主要采用导热油、熔融盐和水作为集热工质，其热力学性能直接影响动力循环参数，从而限制电站循环效率[1]。SiO2、Al2O3、SiC等颗粒物作为集热介质，能够稳定工作在1 000 ℃的高温条件下[2]，且成本低廉，开发潜力巨大。随着太阳能集热器设计水平的提升，使得高参数动力循环技术成为可能，超临界二氧化碳（sCO2）布雷顿循环透平入口温度超过700 ℃，压力超过20 MPa，且结构紧凑、体积小、耗水量低，效率高，极具发展潜力。为了进一步提升sCO2布雷顿循环透平入口参数，提出了基于太阳能颗粒集热的sCO2布雷顿循环系统，采用高温颗粒间接加热sCO2，但所需合金管材昂贵且还需额外消耗电能。因此，颗粒-sCO2换热器的设计应该满足材料消耗少、低能耗以及换热性能优良的要求。

目前，基于颗粒集热的太阳能光热发电系统的颗粒换热器主要类型有移动床和流化床。国内外学者对这2种换热器进行了研究[3-10]。Baumann等人[3]提出一种应用于以固体颗粒为储热介质的移动床水平埋管换热器，实验测得颗粒侧传热系数仅为100~250 W/(m2·K)。Clifford等人[4]建立了一种平板移动床sCO2传热模型，并且实验测量平板颗粒重力流的壁面换热系数约为200 W/(m2·K)。

虽然移动床换热器具备结构紧凑、操作简单等优势，但颗粒侧传热系数较低，显著增加了换热材料投入成本，而流化床换热器具备优良的换热性能，适合作为sCO2换热器。Weast和Shannon等 人[5]提出多级流化床适合作为储热系统的换热器。Schwaiger等人[6-8]提出了一种流化床换热器设计，并分别建立了200 MW蒸汽发生器和121 MW sCO2换热器的设计方案。Ma等人[9]建立了100 kW超临界流化床换热器模型，分析了管子尺寸和换热系数对管材消耗成本的影响。Gomez-Garcia等人[10]建立了基于太阳能颗粒集热的蒸汽朗肯循环系统，并优化了预热段、蒸发段、过热段和再热段中多级流化床换热器的配置参数。这些研究中：一方面颗粒侧的传热模型较为简单，无法精确反映颗粒侧传热系数；另一方面缺乏对各项损失的评估参数设计。为此，本研究应用更加精确的颗粒侧传热模型，构建一个细致的sCO2流化床换热器模型，以100 kW换热等级换热器为例评估运行和结构参数对换热器管材尺寸、风机能耗、流动压损和热效率等因素的影响，以期望为大型sCO2流化床换热器的设计和运行提供参考。

1 系统描述

图1为典型的基于太阳能颗粒集热的sCO2布雷顿循环系统。该系统由镜场、颗粒集热储热系统、sCO2流化床换热器、sCO2布雷顿循环系统组成。颗粒通过太阳能颗粒集热器吸收汇聚的太阳辐射升温，高温颗粒输运至热罐，然后高温颗粒经过sCO2换热器将热量传递给CO2，颗粒经过换热后输送至冷罐，继续循环至颗粒集热器吸收太阳 能辐射。吸收颗粒热量的sCO2经过高压透平做功，然后经过再热器再次进入低压透平做功，最后经过回热器和冷却器后进入流化床换热器，开始新的循环。

图1 基于太阳能颗粒集热的sCO2布雷顿循环光热发电系统

2 流化床换热器模型

2.1 物理模型

图2为逆流形式流化床换热器模型。高温颗粒从一侧进入床体，sCO2工质从另外一侧流入错列排布管束，流化气体通过床体底部的布风板进入流化区域，颗粒将热量通过管壁传递给管内sCO2工质后，低温颗粒从出口侧离开，高温sCO2工质从换热器另一侧离开至透平做功，流化气体从顶部离开。入口流化气体在空气回热器内经换热器出口的高温流化气体加热升温。流化床换热器管束呈错列等边三角形布置。计算模型将换热器沿CO2流动方向进行离散化。

图2 逆流形式sCO2流化床换热器模型

2.2 模型初始参数

模型采用CARBO Accucas颗粒[11]。模型假设：换热器颗粒入口温度为775 ℃，出口温度为570 ℃；CO2入口温度为550 ℃，CO2出口温度约为700 ℃，入口压力为20 MPa；统一空气入口压力为131.3 kPa，出口压力为101.3 kPa。各物性计算通过调用REFPROP9.0软件来实现。表1列出了模型初始参数。

表1 模型初始参数

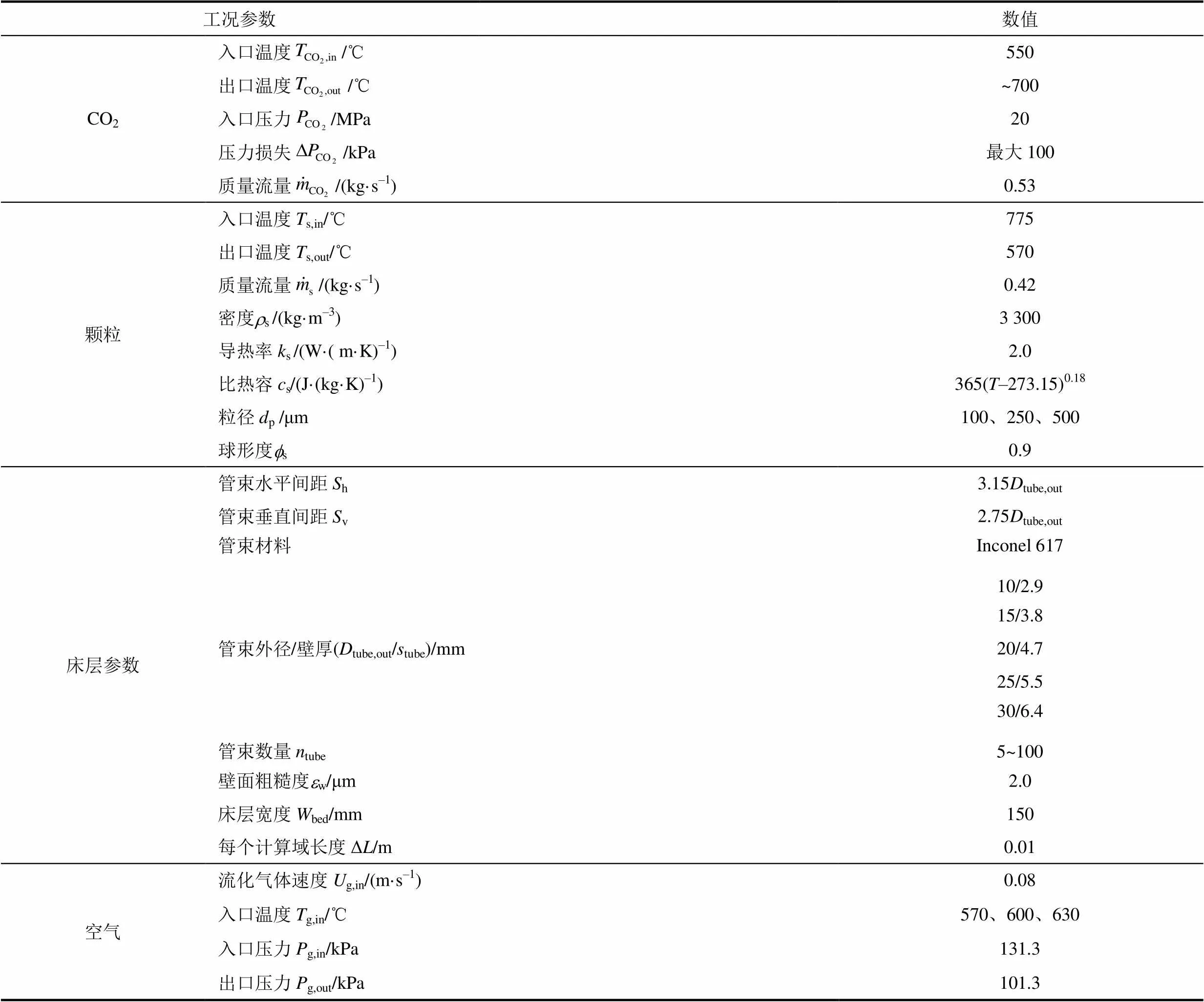
Tab.1 The initial parameters for modelling

注：表示颗粒温度，K。

给定基础工况参数后，传热模型中可优化的参数为传热管束尺寸（外径、壁厚）、管束数量、颗粒粒径、流化气体入口温度。在优化计算中，满足CO2流动损失的前提下，以管材消耗质量最小作为管径和管束数量选择的优化目标，颗粒粒径和流化气体入口温度以最大换热器热效率为优化目标。

2.3 数学模型

2.3.1颗粒侧传热系数

流化床对埋管壁面传热系数采用Kim学者的鼓泡床埋管传热模型[12]，其模型描述如下。

鼓泡流化床设计最主要的参数是临界流化速度，可以由式(1)求解：

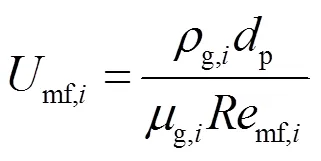
式中：下标表示第段离散计算域；mf,i表示临界雷诺数，根据Boissière[13]的研究，其值由Thonglimp[14]表达式确定，

式中g,i表示阿基米德数，

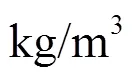
根据Kim等人[12]的实验研究结果，顶部管束的努塞尔数top,i为

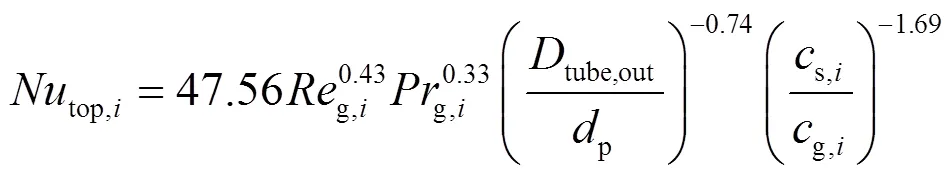
式中：g,i为流化气体雷诺数；g,i为流化气体普朗特数；s,i为颗粒定压比热容，J/(kg·K)；g,i为空气定压比热容，J/(kg·K)。

则顶部管束的对流传热系数由颗粒粒径p和流化气体热导率g,i决定，

底部管束的对流传热系数[15-16]为

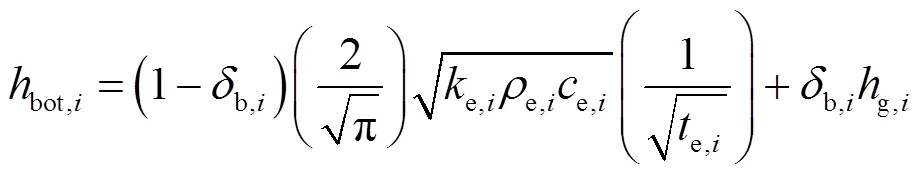
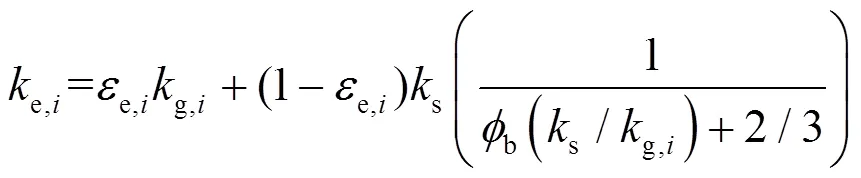
式中：b,i为乳化相中气相体积分数，e,i为乳化相平均接触时间的平方值[17]，*表示气体流通面积与床层面积的比值，1为管束在布风板截面的垂直投影面积，2为布风板截面面积，e,i为乳化相密度，e,i表示乳化相的空隙率[18]，e,i为乳化相导热率[19]，b为颗粒间接触点附近的气膜等效厚度[19]。

因为流化气体是空气，乳化相中颗粒的质量远远大于气体的质量，所以乳化相比热容e,i可以近似等于颗粒比热容s,i。

气泡相传热系数g,i[14]由式(13)得到，

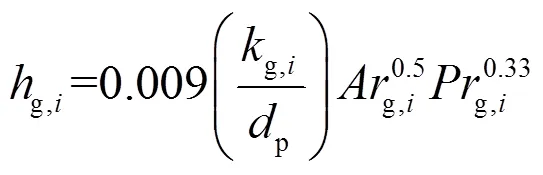
水平埋管颗粒侧平均传热系数e,i由式(14)计算，

2.3.2 sCO2侧传热系数

管内流动为单相流，sCO2侧传热系数由努塞尔数决定，可依据Gnielinski[20]湍流传热经验公式计算得到，

2.3.3 传热模型计算

根据对数平均温差法，第段中颗粒与sCO2气体换热量为：

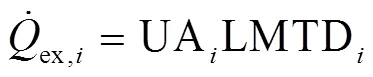
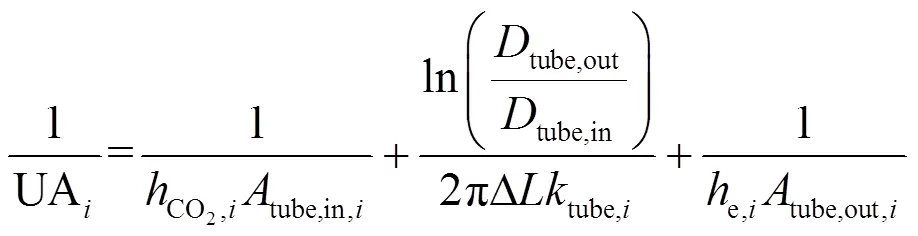
式中，LMTD为第段的对数平均温差，UA为总传热热阻。

根据能量守恒定律有：

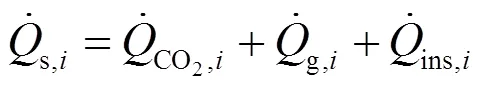
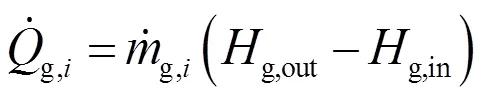
假定第段计算域中流化气体的出口温度g,out,i等于颗粒的出口温度s,out,i，流化气体以恒定温度g,in进入床层计算域。那么，通过式(21)和式(22)可以得到第段计算域中颗粒的入口温度s,in,i，

换热器热效率th为

2.3.4 CO2压力损失

第段计算域的CO2出口压力为

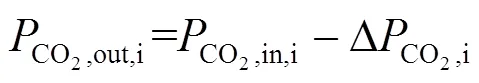
2.3.5 气体压力损失及风机能耗

气体压力损失Δair主要由布风板压损Δdist、床层压降Δs和风道压损Δtube三部分组成。

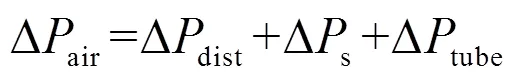
单一颗粒流化床床层压损主要由床层高度和临界流化速度下的床层空隙率决定[21]：

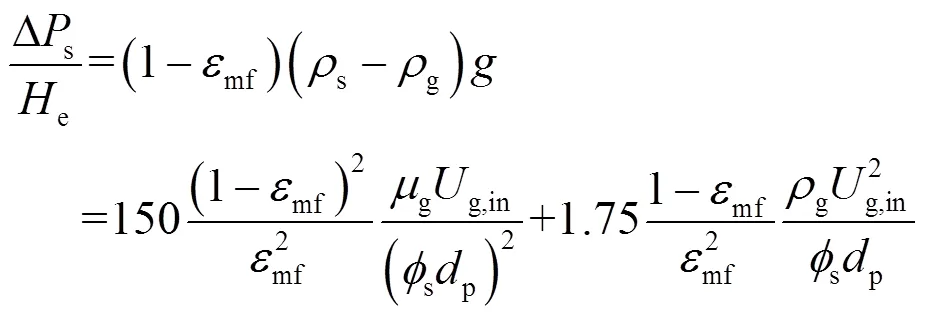
式中：Δs为床层压降，Pa；e为床层高度，m；s为颗粒密度，kg/m3；g为气体密度，kg/m3；g,in为流化气体速度，m/s；g为气体动力黏度，Pa·s；p为颗粒粒径，m；mf为临界流化速度下的床层空隙率；s为颗粒球形度；为重力加速度，9.81 m/s2。

为了整个床层截面布风均匀，布风板压降Δdist一般取床层压降的1/3。本模型中忽略风道压 损Δtube。

流化床风机能耗是重要的运行参数，主要由气体压损和气体流量决定。为了评估风机能耗，假定流化气体是理想气体，取风机效率comp=0.75，风机能耗为

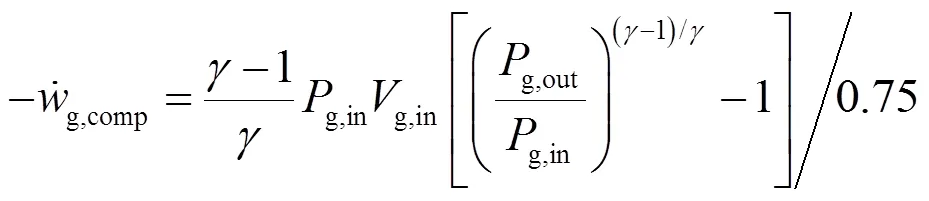
式中：g,in为气体入口压力g,in=Δg+g,out，Pa；g,out为床层出口压力，Pa；g,in为气体入口体积流量，m3/s；为理想气体指数，取1.4。

3 模型计算与分析

假设在每个计算域的进出口截面上，颗粒、CO2和空气的流量、温度分布均匀。利用MATLAB2014a软件进行迭代计算，整个计算域的收敛条件为颗粒入口温度到达换热系统颗粒入口温度s,in，第段计算域的收敛条件为满足上述传热模型。第段计算域的迭代计算过程如图3所示。

图3 第i段迭代计算过程

3.1 管径、管束数量的影响

计算管长是衡量管材消耗和换热器占地面积的重要参数，选取颗粒粒径为250mm，流化气体入口温度为630 ℃，流化气体速度为0.08 m/s，传热管外径、管束数量与计算管长之间的关系如图4所示。由图4可见，随着管束数量从5根增至100根，传热计算管长逐渐减小，管材消耗质量逐渐增加。

图4 不同管径下计算管长和管束数量的关系

管径和管束数量的选择除了考虑管材消耗质量以外，还需要考虑允许的管内流动压力损失。表2列出了在满足最大允许CO2压力损失0.01 MPa的前提下不同管径对应参数。由表2可以看出，管外径取10 mm，管束数量为97根时，管束布置可以满足床层压力损失30 kPa的设计要求，计算管长为2.65 m，CO2压力损失为9.874 kPa，CO2出口温度为702 ℃，风机能耗为113.62 W，热效率为99.64%。因此，选取管束外径为10 mm，管束数量97根作为分析的管束参数。

3.2 颗粒粒径的影响

在管外径为10 mm，管束数量为97根，流化气体入口温度为630 ℃，流化风速为颗粒出口温度条件下2倍的临界流化风速条件下，计算不同颗粒粒径的气体热损失和换热器效率，结果如图5所示。由图5可见，当颗粒粒径分别为100、250、500mm，流化气体热量损失分别为70.32、365.24、1 176.00 W，风机能耗分别为21.60、113.62、405.97 W，换热器热效率分别为99.93%、99.64%、98.84%。可见，随着颗粒粒径的增大，临界流化速度增加，流化气体流量增加，气体热损失越大，换热器热效率越低。这是由于颗粒粒径增加导致的临界流化风速提升会显著增加风机能耗，使得整个电站厂用电效率降低。因此，选择小粒径颗粒对换热器效率提升和电厂性能提升具有重要意义。

表2 在满足最大允许CO2压力损失0.01 MPa前提下不同管径对应参数

Tab.2 The relevant parameters corresponding to different tube diameters on the premise of satisfying the CO2’s maximum allowable pressure loss of 0.01 MPa

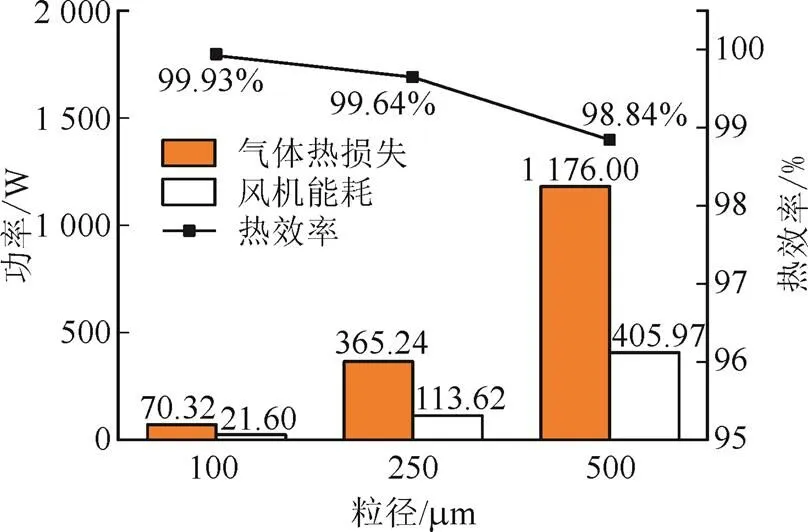
图5 不同颗粒粒径的气体热损失和换热器效率

3.3 流化气体入口温度的影响

在管外径为10 mm，管束数量为97根，颗粒粒径为250mm，流化风速为0.08 m/s条件下，计算不同流化气体入口温度的气体热损失和换热器热效率，结果如图6所示。由图6可见，当流化气体入口温度分别为570、600、630 ℃时，气体热损失分别为1 498.74、922.23、365.24 W，换热器热效率分别为98.52%、99.09%、99.64%。可见，提升流化气体入口温度，能够降低气体热损失，提升换热器效率。因此，在电站系统中，配置空气回热器回收流化气体热量是十分必要的，同时应该尽量降低空气回热器热端差，以提升换热器效率。

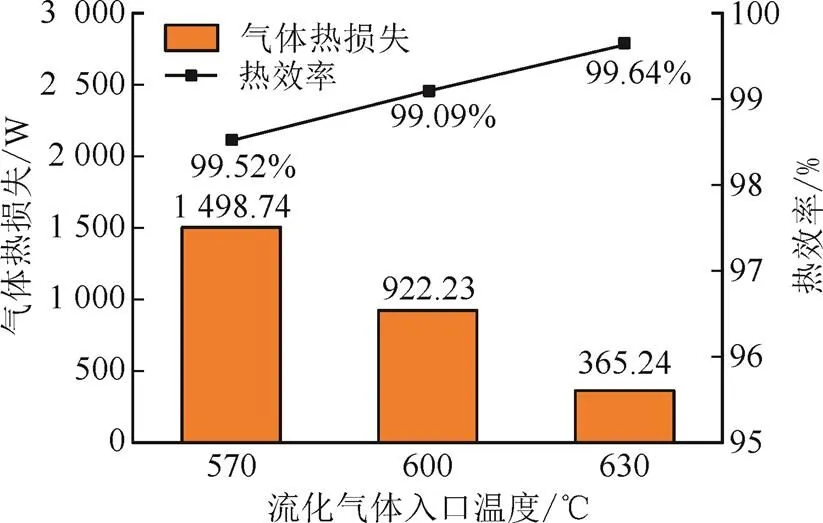
图6 不同流化气体入口温度的气体热损失和换热器效率

4 结 论

1）本文构建了基于太阳能颗粒集热的超临界二氧化碳布雷顿循环系统的流化床换热器模型。以换热等级为100 kW的流化床换热器为原型，在基准工况下，对传热管外径、管束数量、颗粒粒径和流化气体入口温度等参数进行优化

2）综合考虑换热器管材消耗和CO2压力损失两个因素，换热器设计方案定为管子外径为10 mm，壁厚为2.9 mm，管束数量为97根。此时的CO2压力损失为9.874 kPa，计算管长为2.65 m，管材消耗质量为139.0 kg，CO2出口温度为702.0 ℃，风机能耗为113.62 W，热效率为99.64%。

3）换热器选择颗粒粒径越小，临界流化速度越低，从而导致流化气体流量越小，气体热损失越小，换热器热效率越高，并且可以显著降低风机能耗，提升厂用电效率。提高换热器流化气体入口温度，有利于提升换热器热效率，流化气体入口温度从570 ℃提升到630 ℃，可使换热器热效率从98.52%提升至99.64%。因此，需要尽量降低空气回热器热端差，以提高流化气体入口温度。

［1］ LIU M, TAY N H S, BELL S, et al. Review on concentrating solar power plants and new developments in high temperature thermal energy storage technologies[J]. Renewable & Sustainable Energy Reviews, 2016, 53: 1411-1432.

［2］ HO CLIFFORD K. A review of high-temperature particle receivers for concentrating solar power[J]. Applied Thermal Engineering, 2016, 109: 958-969.

［3］ BAUMANN T, ZUNFT S. Development and performance assessment of a moving bed heat exchanger for solar central receiver power plants[J]. Energy Procedia, 2015, 69: 748-757.

［4］ ALBRECHT K J, HO C K. Heat transfer models of moving packed-bed particle-to-SCO2heat exchangers[C]. ASME 2017 11th International Conference on Energy Sustainabilit: V001T05A006. DOI: 10.1115/ES2017-3377.

［5］ WEAST T, SHANNON L. Thermal energy storage systems using fluidized bed heat exchangers[R]. Report NASA-CR-159868, DOE/NASA/0096-1, 1980.

［6］ STEINER P. Experimental investigations and application analysis of a particle-based high temperature thermal energy storage[D].Wien: TU Wien, 2017: 50.

［7］ SCHWAIGER K, HAIDER M, HAEMMERLE M, et al. Fluidized bed steam generators for direct particle absorption CSP-plants[J]. Energy Procedia, 2015, 69: 1421-1430.

［8］ STEINER P, SCHWAIGER K, WALTER H, et al. Fluidized bed particle heat exchanger for supercritical carbon dioxide power cycles[C]//ASME 2016. ASME International Mechanical Engineering Congress and Exposition, Volume 14: Emerging Technologies; Materials: Genetics to Structures, Safety Engineering and Risk Analysis: V014T07A014. DOI: 10.1115/IMECE 2016-67104.

［9］ MA Z, MARTINEK J. Fluidized-bed heat transfer modeling for the development of particle/supercritical-CO2heat exchanger[C]//ASME 2017. ASME 2017 11th International Conference on Energy Sustainability: V001T05A002. DOI: 10.1115/ES2017-3098.

［10］ GOMEZ-GARCIA F, GAUTHIER D, FLAMANT G. Design and performance of a multistage fluidized bed heat exchanger for particle-receiver solar power plants with storage[J]. Applied Energy, 2017, 190: 510-523.

［11］ HO C K. Characterization of particle flow in a freefalling solar particle receiver[C]//ASME 2015. ASME 2015 9th International Conference on Energy Sustainability, ES 2015, collocated with the ASME 2015 Power Conference, the ASME 2015 13th International Conference on Fuel Cell Science, Engineering and Technology, and the ASME 2015 Nuclear Forum. 2015.

［12］ KIM S W, AHN J Y, KIM S D, et al. Heat transfer and bubble characteristics in a fluidized bed with immersed horizontal tube bundle[J]. International Journal of Heat and Mass Transfer, 2003, 46(3): 399-409.

［13］ BOISSIERE B, ANSART R, GAUTHIER D, et al. Experimental hydrodynamic study of gas-particle dense suspension upward flow for application as new heat transfer and storage fluid[J]. The Canadian Journal of Chemical Engineering, 2015, 93(2): 317-330.

［14］ THONGLIMP V, HIQUILY N, LAGUERIE C. Vitesse minimale de fluidisation et expansion des couches fluidisées par un gaz[J]. Powder Technology, 1984, 38(3): 233-253.

［15］ MICKLEY H S, FAIRBANKS D F. Mechanism of heat transfer to fluidized beds[J]. Aiche Journal, 1955, 1(3): 374-384.

［16］ OZKAYNAK T F, CHEN J C . Emulsion phase residence time and its use in heat transfer models in fluidized beds[J]. Aiche Journal, 1980, 26(4): 544-550.

［17］ BASKAKOV A P, BERG B V, VITT O K, et al. Heat transfer to objects immersed in fluidized beds[J]. Powder Technology, 1973, 8(5): 273-282.

［18］ SAXENA S C. Heat transfer between immersed surfaces and gas-fluidized beds[J]. Advances in Heat Transfer, 1989, 19: 97-190.

［19］ KUNII D, LEVENSPIE O. Fluidization engineering[M]. USA: Butterworth-Heinemann, 1991: 313-336.

［20］ GNIELINSKI V. On heat transfer in tubes[J]. International Journal of Heat & Mass Transfer, 2013, 63(3): 134-140.

［21］ ERGUN S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48: 89-94

Numerical study on heat exchanger of supercritical CO2Brayton cycle fluidized bed boiler based on solar particle-receiver

CHEN Bo, NI Mingjiang, YING Zhenzhen, CEN Kefa, XIAO Gang

(College of Energy Engineering, Zhejiang University, Hangzhou 310027, China)

With high thermal efficiency, the supercritical CO2Brayton cycle system based on solar particle-receiver has great development potential. By applying a more accurate particle-side heat transfer model, the supercritical CO2fluidized bed heat exchanger model is established. On the basis of the operating parameters of the heat exchanger with 100 kW heat transfer power, the external diameter, tube bundle number, particle size and fluidized gas temperature of the heat transfer pipes are optimized. The results show that, under the condition that the flow pressure loss of CO2is 0.01 MPa, the optimized tube bundle parameters of the heat exchanger are as follows: the outer diameter of the tube is 10 mm, the thickness of the tube is 2.9 mm, the number of the tubes is 97. When the small particle size particles are selected, the critical fluidization velocity is low, the flow rate is small, so the heat loss of the gas can be effectively reduced, the heat efficiency of the heat exchanger can be improved, and the energy consumption of the fan can be decreased. With the optimized tube bundle parameters, when the particle size increases from 100 μm to 500 μm, the heat loss increases from 70.32 W to 1 176.00 W, the thermal efficiency declines from 99.93% to 98.84%, the fan power consumption increases from 21.60 W to 405.97 W, the inlet temperature of the fluidized gas rises from 570 ℃ to 630 ℃, and the thermal efficiency of the heat exchanger increases from 98.52% to 99.64%.

solar thermal power generation, supercritical carbon dioxide, fluidized bed, heat exchanger, thermal efficiency, pressure loss, fan power consumption

TK11+2

A

10.19666/j.rlfd.201901002

陈博, 倪明江, 应振镇, 等. 基于太阳能颗粒集热的超临界CO2流化床换热器模拟研究[J]. 热力发电, 2019, 48(7): 70-76. CHEN Bo, NI Mingjiang, YING Zhenzhen, et al. Numerical study on heat exchanger of supercritical CO2Brayton cycle fluidized bed boiler based on solar particle-receiver[J]. Thermal Power Generation, 2019, 48(7): 70-76.

2019-01-16

陈博(1994—)，男，硕士研究生，主要研究方向为太阳能光热发电技术，chenbo_2016@zju.edu.cn。

（责任编辑 杨嘉蕾）