结合邻域信息的TV正则化稀疏角度重建算法

齐泽瑶，王远军

(上海理工大学医疗器械与食品学院，上海200093)

E-mail:yjusst@126.com

1 引言

计算机断层成像(Computed Tomography，CT)是医学影像诊断领域中广泛应用的一种现代成像技术.然而在医疗诊断过程中过度的辐射剂量可能会影响人体的生理机能、增加致癌机率，尤其是对儿童影响更为严重［1］.因此，在临床检查中辐射剂量的控制非常重要.在临床检查过程中剂量的高低控制主要通过X射线的强度和扫描投影的角度数量来调节.当X射线的强度减小时，采集的投影数据会不可避免地引入不稳定噪声，将会导致图像质量下降.而减少投影角度的数量属于不完全投影数据重建问题，是数学理论中的一个病态逆问题［2］.而压缩感知(Compressed Sensing，CS)理论的发展为不完全投影重建提供了新思路:如果图像是稀疏的，或可以找到合适的变换域使其稀疏，则可以通过挖掘其稀疏图像的L1范数准确地重建图像［3］.

在欠采样稀疏投影数据的条件下重建图像时，由于投影信息的不足，采用解析算法，如滤波反投影(filtered back-projection，FBP)算法时会产生混叠伪影，这将极大地影响重建图像的质量;采用传统的迭代重建算法，如代数重建算法(algebraic reconstruction technique，ART)和联合代数重建算法(simultaneous algebraic reconstruction technique，SART)虽然不会受到混叠伪影的干扰可以重建出较清晰的图像，但也会产生一些不符合临床需要的伪影从而无法获得理想的结果;而依据CS理论通过在目标函数中加入惩罚项或正则项时可以进一步改善重建图像的质量，其中以全变分(total variation，TV)作为CS稀疏变换的重建算法取得了很好的重建效果并得到了广泛的研究［4-8］.

2006年，Sidky等［9］将TV模型应用到了图像重建领域，提出了TVM-POCS(total variation minimization-projection onto convex sets)算法，表明了以TV为先验信息作为正则化可以在稀疏投影数据中重建出高质量的图像，但由于图像的分段常数假设，在重建结果图像的边缘和细节区域有时会过于平滑.为了解决这个问题，一些研究学者考虑到各向同性边缘属性的局限性，更充分的利用部分相关先验信息，以权重的形式引入到TV项来利用各向异性边缘属性提高重建算法的性能，并提出相关的算法通过在图像的边缘和平滑区域引入自适应权重保护了图像的边缘和细节信息［10-14］.

Tian等［10］提出 EPTV(TV-based edge preserving)模型，通过局部梯度强度构建自适应的指数权重函数并引入到TV的每一项中，保护了更多的低对比度结构和边缘信息.然而，仅考虑了各向同性边缘属性;Liu等［11］提出AwTV(adaptiveweighted TV)模型，通过局部梯度强度构建自适应的指数权重函数引入到TV模型中的各个梯度的子方向上，考虑了各向异性边缘属性以图像局部信息自适应调整梯度强度，更好的保存了边缘细节信息.然而，也仅仅考虑了图像的局部信息;Zhang等［12］提出了 NLTV(Non-local TV)模型，通过利用图像的非局部自相似性特质构建自适应的权重函数引入到TV模型中，更好的保存了边缘细节.综合考虑局部范围和远程范围的相关性，范围的大小与重建时间成正比，当局部范围较大时耗时较长;Rong等［13］在AwTV模型的基础上提出了EGAwTV(anisotropic edge-guided adaptive-weighted TV)模型，通过检测边缘信息和局部图像强度梯度来构建权重函数，引入更多的先验信息进一步保存了图像的边缘和细节信息.然而，仅仅考虑了图像的一阶信息;Zheng等［14］提出了TACTV(total absolute curvature TV)模型，将曲率的绝对值引入到TV模型中，利用图像的二阶信息能够更好地描述特征复杂的图像等等.

受到上面提及思想的启发，本文在传统的TV重建算法的基础上引入一个权重来自适应的调节横向梯度和纵向梯度在TV中的占有比.其中的权重大小取决于每个像素邻域区域内的均值和均方差.通过像素邻域信息的均值和均方差构建而成的自适应权重利用各向异性边缘属性来改进传统TV重建算法的性能.

2 本文算法

2.1 TV重建算法

CT图像重建的数学模型通常采用线性方程组来描述，模型的离散形式表示为:

其中，p为投影向量，f为待重建图像向量，系统矩阵A关联了图像向量f和投影向量p，其元素通常被设置为射线路径与路径上相关像素的相交长度［15］.CT图像重建的问题可以表达为根据系统矩阵A和投影向量p来确定未知图像向量f.2004年，Candes等提出的CS理论证明了稀疏信号可以从远小于奈奎斯特采样要求的采样数据中被重建.因此，在迭代重建算法求解时，可以应用包括图像稀疏性的一些先验信息［16］.CS理论在CT重建中的应用可以将重建问题表示为带约束的优化问题:

对于医学图像来说大部分是非稀疏的，而图像中某些结构的边缘处经常发生急剧的强度变化，可以通过离散梯度变换进行稀疏表示［3］.因此，稀疏投影数据重建经常采用TV(图像梯度的L1范数)作为目标函数进行图像的优化［9］: 表示图像在(s，t)处的像素值，s和t分别表示横向和纵向坐标.

2.2 本文算法

为了进一步改善TV重建算法的性能，本文通过联合图像像素邻域信息的均值和均方差利用各向异性边缘属性提出了一种结合邻域信息的TV正则化稀疏角度重建算法.自适应权重函数构建原则如下［17］:遍历原图像，以每个像素点为中心，计算其邻域内像素的均值和均方差，然后计算出权值系数 ws，t:

其中，

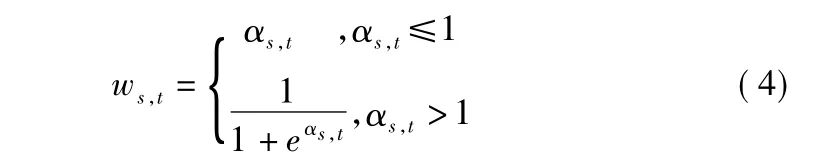
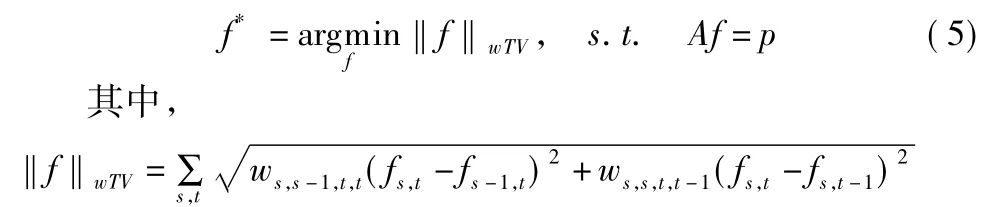
自适应权重 ws，s－1，t，t和 ws，s，t，t－1分别以横纵方向上的梯度图像为基础，采用公式(4)构建而成.

TV重建算法将图像作为一个整体考虑，有效的利用了图像的稀疏性和边缘方向先验信息，能够在稀疏投影采样的条件下重建出质量较高的图像，然而由于各向同性边缘属性的局限性不能充分的调整局部信息，重建图像往往会出现边缘过于平滑的现象.而本文提出的重建算法采用权重函数自适应的调节横向梯度和纵向梯度在TV中的占有比利用各向异性边缘属性打破了局限性.

图像中每个像素在相同邻域大小的区域内分布都是不同的，这里我们给定一个系数w来表示它们之间的不同.而均值和均方差可以较好的体现各个像素邻域区域内像素的分布以及变化程度.均值表示邻域区域内像素整体的分布水平，均方差表示大部分像素值和其均值的偏离程度反映了邻域区域内像素波动大小的程度.当邻域区域内像素值大小越接近时说明此区域越趋于平滑，均方差越小，反之均方差越大.这两者共同反映了图像像素邻域区域的系数w的大小，从而在不同像素邻域区域内进行不同尺度的正则化实现了局部信息的调整.

2.3 本文算法实现及步骤

受到传统TV重建算法实现的启发，本文算法实现也采用最速下降法求解此优化问题.当图像质量远远达不到理想的效果时，图像像素邻域区域的均值和均方差会受到很大的影响.本文算法的实现过程分为两部分:在执行梯度下降算法选择下降方向优化图像时，首先使用传统的TV作为下降方向，当迭代一定的次数后再选择带权重的TV作为下降方向.本文算法实现的主要步骤如下:

1)初始化重建参数:

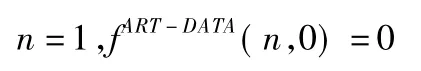
其中，n≤N是算法当前迭代的次数，N是总的迭代次数.

2)利用ART算法重建过渡图像:

其中，λ 是松弛因子，m=1，…，Ndata，Ndata是所有投影角度总的射线条数.

3)对重建图像进行非负性约束:

4)选择像素邻域区域大小，计算权重:

5)利用梯度下降算法优化图像，其中l=1，2，…，M:

5-3)更新重建图像f:

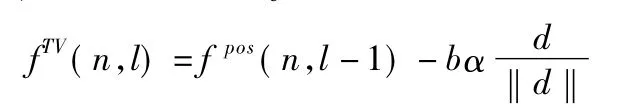
其中，M为梯度下降算法的迭代次数，k是算法迭代TV的总次数，ξ是为了防止分母为零而设置的一个很小的正数，这里设置为ξ=10－8.

6)循环2)-5)，直到满足收敛标准或得到最大迭代次数为止，本文中我们设置达到迭代次数N为停止迭代标准.

3 数值仿真

为了研究本文算法在欠采样稀疏投影采样的条件下重建的可行性，我们在此章节对仿真数据Shepp-Logan体模［18］和真实的核桃投影数据［19］进行重建实验.所有实验测试使用的电脑配置为 Intel(R)Core(TM)i7-7700 CPU，主频为3.60GHz，运行内存为 8GB，操作系统为 Windows 8，测试平台为MATLAB 2016b.

3.1 Shepp-Logan体模仿真实验

本章节实验以Shepp-Logan模型模拟生成基于圆形轨道的扇形束投影数据，仿真模型的大小设为256*256.在模拟环境中，使用等角虚拟探测器，扇角设为π/4，射线源与旋转中心的距离设为512mm，探测器通道数设置为256个.在2π范围内对体模进行均匀采样，分别获取24、36、48个投影数据.重建过程中的重建参数设置为:总的迭代次数N=200，ART迭代算法的松弛因子λ=0.25，像素邻域区域的大小p*q=3*3，TV 的迭代次数为 k=50，α =0.2，M=20.图 1 为TV算法和本文算法重建得到的结果图像.

图1 TV算法(第1行)和本文算法(第2行)从24(第1列)、36(第2列)、48(第3列)个无噪声投影数据重建的结果图像;第3行和第4行分别是TV算法和本文算法结果图像的感兴趣区局部放大显示Fig.1 Reconstructed results of the TV algorithm(1st line)and our algorithm(2nd line)from 24(1st column)，36(2nd column)and 48(3rd column)noise-free projection data.The 3rd line and 4th line are respectively the corresponding zoomed in part display of ROI of the result image of the TV algorithm and our algorithm

从图1中的第1行和第2行我们可以看出两种迭代算法在不同的投影数据下重建图像都基本无伪影，但在投影数据较少时的重建图像在边缘的细节区域显示较模糊，而投影数据较多时的重建图像在边缘的细节区域显示较清晰，在视觉效果上与原始的Shepp-Logan体模基本无差异.为了能够更好的比较两种算法，部分感兴趣区域已经被白色虚线框标出并且放大显示在图1的第3行和第4行中，从中可以清晰的发现，本文算法无论是在投影数据较少时还是在投影数据较多时，重建的结果图像边缘都比TV算法重建的结果图像清晰.因此，本文算法可以重建出质量高于TV算法的图像.为了进一步验证本文算法的优越性能，利用均方根误差(root mean square error，RMSE)表明算法的重建精度.RMSE定义如下:

其中，fj和gj分别表示原图像向量和重建图像向量，RMSE通常用来评估重建图像的精确度，它的取值范围为0-1，其值越接近0表明重建精度越高.

图2给出了两种重建算法分别在24、36和48个无噪声投影数据下重建结果关于RMSE随迭代次数增加的变化曲线图.本文算法前k=50次迭代选择TV下降方向进行迭代，因此前面RMSE下降趋势相同.但在图2中可以清晰看出，本文算法比TV重建算法在相同的迭代次数时重建结果误差较小.综合前面的分析，可以得出本文算法具有比TV重建算法更加卓越的重建性能.

图2 TV算法和本文算法在24(第1列)、36(第2列)、48(第3列)个无噪声投影数据下重建结果关于RMSE随迭代次数增加的变化曲线Fig.2 Under the condition of 24(1st column)，36(2nd columns)and 48(3rd columns)noise-free projection data，the RMSE curves of the reconstructed image of TV algorithm and our algorithm changes with the increase of iterations

3.2 算法抗噪声性能的验证

为了验证算法的抗噪声性能，在获得的Shepp-Logan模型投影数据中加入一个随机噪声，然后分别降采样为24、36和48个含有噪声的投影数据，采用TV重建算法和本文算法进行重建实验.重建过程中的重建参数设置与2.1节一致.两种重建算法的结果图像和部分感兴趣区域局部放大部分显示在图3中.

图3 TV算法(第1行)和本文算法(第2行)从24(第1列)、36(第2列)、48(第3列)个含噪声投影数据重建的结果图像;第3行和第4行分别是TV算法和本文算法结果图像的感兴趣区局部放大显示Fig.3 Reconstructed results of the TV algorithm(1st line)and our algorithm(2nd line)from 24(1st column)，36(2nd column)and 48(3rd column)noise projection data.The 3rd line and 4th line are respectively the corresponding zoomed in part display of ROI of the result image of the TV algorithm and our algorithm

从图3中我们可以看出重建图像基本没有伪影，在相同迭代次数下重建图像的边缘区域随着投影数据的增加而逐渐的清晰.对比图1和图3可以从感兴趣区域看出，在边缘处不如无噪声投影数据重建结果清晰.从图3中也可以清晰的看出相同数量的投影数据重建结果中，本文算法重建的结果图像比TV重建算法重建的结果图像边缘处较清晰.图4给出了两种重建算法分别在24、36、48个含噪声投影数据的条件下重建的结果关于RMSE随迭代次数增加的变化曲线.可以看出本文算法比TV重建算法更快的收敛，且重建结果误差较小.这与在无噪声的投影数据重建实验结果一致.因此，我们可以得出本文算法比TV算法具有更好的重建性能和更快的收敛速度.

图4 TV算法和本文算法在24(第1列)、36(第2列)和48(第3列)个含噪声投影数据下重建结果关于RMSE随迭代次数增加的变化曲线Fig.4 Under the condition of 24(1st column)，36(2nd columns)and 48(3rd columns)noise projection data，the RMSE curves of the reconstructed image of TV algorithm and our algorithm changes with the increase of iteration

3.3 真实的投影数据重建

为了更进一步验证算法性能，本文对获得的真实CT投影数据进行稀疏角度重建实验.被检测的物体为一个核桃模型，投影数据是用德国菲尼克斯(Phoenix|X-Ray)X射线检测系统与服务有限公司提供专有的μCT成像系统扫描获得.其中，射线源到平板探测器的距离为300mm，射线源到扫描物体的距离为110mm，平板探测器的宽度为114.8mm.在管电压为80kV，管电流为200μA时的状态下以圆轨迹锥束扫描进行投影数据的获取.然后降采样分别获得30、60、120个角度的投影数据.

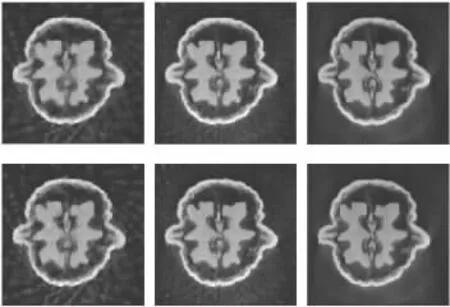
图5 TV算法(第1行)和本文算法(第2行)从30(第1列)、60(第2列)、120(第3列)个投影数据重建的结果图像Fig.5 Reconstructed results of the TV algorithm(1st line)and our algorithm(2nd line)from 30(1st column)，60(2nd column)and 120(3rd column)projection data

本文对z轴上的中心切片进行重建，TV算法和本文算法重建参数设置与仿真实验一致，重建结果和部分感兴趣区局部放大如图5和图6所示.从图5中可以看出重建的结果图像随着投影数据的增加，虽然边缘有模糊的现象但在相同迭代次数下图像质量越来越好.结合图6显示的部分感兴趣区的局部放大图可知在视觉效果上本文算法的重建结果较优.

图6 TV算法(第1行)和本文算法(第2行)从30(第1列)、60(第2列)和120(第3列)个投影数据重建结果图像感兴趣区Fig.6 Region of interest of reconstructed results of the TV algorithm(1st line)and our algorithm(2nd line)from 30(1st column)，60(2nd column)and 120(3rd column)projection data

4 结论

本文在稀疏角度投影数据的条件下，针对传统的TV算法的局限性提出了一种结合邻域信息的TV正则化稀疏角度重建算法.与TV重建算法相比，本文算法通过像素邻域区域的均值和均方差引入了一个权重，考虑了图像的各向异性边缘属性，使图像的局部信息可以进行自适应的调整，并运用最速下降法进行求解，更好的提高了重建图像的质量.并且以Shepp-Logan仿真模型和核桃的真实投影数据进行了重建实验，实验结果也表明了本文算法的优越性能，可以在抑制伪影的同时更好地保留边缘结构信息，重建更精确的图像，验证了本文提出的算法的有效性.

本文只对仿真实验和核桃中心层面的图像进行了重建，实验数据有限，有待进一步深入研究.另外，本文重建算法采用梯度下降法求解，耗时长，可以进一步改进现有技术，如基于GPU的加速技术和新的求解算法.此外，我们将尝试探索有限角度投影重建问题，以减少辐射剂量.