基于协方差稳健模糊线性回归的系统负荷预测数学模型

孙珍

摘  要： 针对统计学中基于线性回归分析的系统负荷准确预测问题，提出一种基于协方差改进稳健模糊回归的预测数学模型。通过引入协方差参数估计，对传统基于均值参数的稳健估计方程进行改进，以便降低对数据中异常点的敏感性，并对多元正态变量的渐近性质进行分析。结合模糊线性回归，将预测结果划分在一个合理的模糊区间，从而进一步排除异常点。实例测试结果表明，相比传统的模糊线性回归模型，提出的稳健模糊回归模型能够有效降低异常数据的影响，降低预测误差。

关键词： 预测数学模型; 线性回归分析; 负荷预测; 稳健估计; 渐近性质分析; 模糊回归

中图分类号： TN911.1?34; TP393                     文献标识码： A                  文章编号： 1004?373X（2019）15?0094?03

System load forecasting mathematical model based on

covariance robust fuzzy linear regression

SUN Zhen

（Ankang University， Ankang 725000， China）

Abstract： In allusion to accuracy problem of system load prediction based on linear regression analysis in statistics， a predictive mathematical model based on covariance improved robust fuzzy regression is proposed. The robust estimation equation based on mean parameter is improved by introducing covariance parameter estimation， so as to reduce the sensitivity to the abnormal points in the data. The asymptotic property of the multivariate normal variables is analyzed. The prediction results are divided into a reasonable fuzzy interval in combination with fuzzy linear regression， so as to further eliminate the abnormal points. The example test results show that in comparison with the traditional fuzzy linear regression model， the proposed robust fuzzy regression model can effectively reduce the influence of abnormal data and effectively reduce the prediction error.

Keywords： forecasting mathematical model; linear regression analysis; load forecasting; robust estimation; asymptotic property analysis; fuzzy regression

0  引  言

随着我国经济持续快速发展，各行各业对能源的需求也日益增长，导致对电网和配电管理系统的现代化要求逐渐提高。电网运行的稳定控制和实时调度决策关系到整个系统的安全性和经济效益，而预测是决策和控制的前提和基础，因此系统负荷预测是电网和配电管理系统的重要组成部分。准确的系统负荷预测已经得到了广泛的关注，并成为现阶段电力行业研究的热点方向[1?2]。

系统负荷数学预测模型需要对历史数据进行趋势归纳，并对各种相关因素之间的内在联系进行分析，以便实现对未来变化情况的准确估计。传统的预测方法主要分为两种类型[3]：基于统计方法的系统化负荷预测和基于人工智能的系统负荷预测。前者中最为经典的是回归分析预测方法，通过探索自变量与因变量之间的逻辑联系，得出回归数学方程，具体又分为线性回归和非线性回归[4]。文献[5]提出基于多元和逐步线性回归的玉米生物量预测模型，并进行了交叉结果验证。文献[6]对传统的月售电量预测线性回归模型进行改进，提高了随机变动下的预测精度。文献[7]采用多个非线性回归模型对房地产价格进行估计并给出金融分析。

上述研究提出线性回归均对预测数值的历史数据和相关影响因素进行了统计分析，但实际情况中存在大量的异常测量数据。而现有的线性回归预测模型均对异常数据点十分敏感，过多的异常数据点将大幅降低预测的精确度和可靠性。然而，模糊线性回归具有较强的稳定性。此外，一般的稳健估计，大多数只对均值参数进行计算，没有考虑到协方差参数的影响，从而忽略了异常点的负面效应。因此，本文对传统稳健估计方法进行改进，增加协方差参数的估计。并将改进后的稳健估计与模糊线性回归相结合得到稳健模糊回归预测模型，从而降低异常点对系统负荷的预测结果影响，得到良好的准确度。

1  回归分析预测方法原理

1.1  线性回归分析法介绍

目前，回归分析预测方法主要分为线性回归和非线性回归，本文研究的主要内容为线性回归分析方法。基于线性回归分析的预测原理为[8]：

式中：[y（t）]表示时刻[t]的预测值;[xip]表示预测相关的各种因素，即随机自变量;[bp]表示回归方程的回归系数;[θ（t）]表示随机干扰，一般服从正态分布。

1.2  模糊线性回归模型

在线性回归分析的基础上，文献[9]通过模糊集的概念提出短期模糊线性回归的预测模型：

传统基于线性回归分析的预测方法实现较为简单，参数少[9?10]。而基于模糊线性回归分析的预测方法提高了稳定性，但是仍对数据中的异常点较为敏感，导致鲁棒性不高，影响实际应用场景的适用性。

2  稳健模糊回归预测数学模型

在上述基于模糊线性回归分析的预测方法基础上，本文引入了稳健估计理论，以便提高预测的鲁棒性。

2.1  稳健估计

假设数据集的数量为[m]，第[i]个参数有[ni]次观察数值，共有[n]次观测记录，则第[i]个参数在时刻[t]观察到的结果为：

2.2  包含协方差参数的稳健估计改进

本文采用改进的稳健估计方程分别估计参数[δ0]和协方差参数[γ0]，如式（5）和式（6）所示：

2.3  渐近性质分析

接下来采用多元正态变量对[f0]和[γ0]的渐近性质进行分析。

2.4  預测算法步骤

采用改进的稳健估计结合模糊线性回归分析实现负荷预测，具体步骤如下：

步骤1：估计参数[δ0]和协方差参数[γ0]初始化。

步骤2：在第[j]次迭代中设定[γ=γj-1]且[δ=δj]，并分别按照式（5）和式（6）求解得到[δj]和[γj]。

步骤3：[j=j+1]，重复步骤2直到迭代至收敛，从而得到[δ]和[γ]。

步骤4：检测是否存在异常值并进行分类。

步骤5：按照如下公式构建稳健模糊回归模型：

式中[μYx]表示模糊数[Y]的隶属度函数。

步骤6：通过最小二乘方法对式（12）进行求解。

步骤7：输出稳健的模糊区间。

3  仿真结果与分析

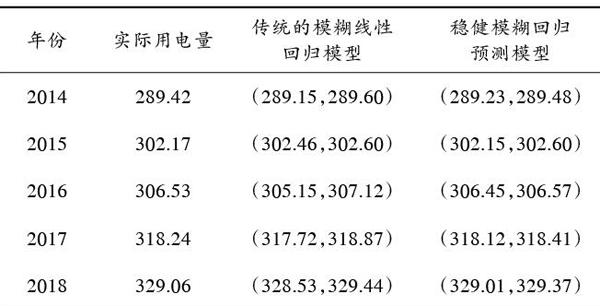
将本文提出的稳健模糊回归预测数学模型、传统的模糊线性回归模型[14]，分别对某省会城市2014—2018年的电力负荷历史数据进行区间预测。两种预测模型的系统负荷估计区间结果如表1所示。

表1  系统负荷估计区间对比

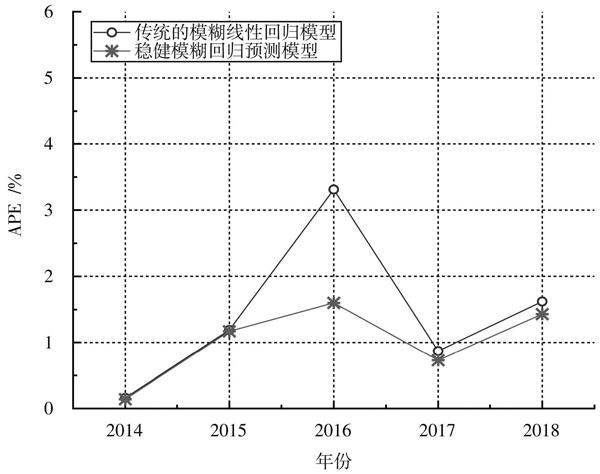
2014—2018年，两种预测模型的绝对百分比误差结果如图1所示。从表1和图1可以看出，稳健模糊回归预测模型的系统负荷预测数值与该时刻的真实数值更接近，预测误差更小。特别是2016年，这是因为该年原始系统负荷数据中的异常点相对较多，导致传统的模糊线性回归模型受到较大的干扰。但是，稳健模糊回归预测模型由于采用包含协方差参数的稳健估计，将异常点几乎全部排除在估计区间之外，从而能够以较高的准确度和鲁棒性完成预测。

图1  误差结果对比

4  结  语

本文提出一种对传统稳健估计方法进行改进的方法，增加了协方差参数估计。并将改进后的稳健估计与模糊线性回归相结合得到稳健模糊回归预测模型，从而降低异常点对系统负荷的预测结果影响，有效降低了预测误差，增加鲁棒性。但是本文提出模型在处理纵向型数据时稳健性不够理想，因此在以后的研究中将针对B?样条方法的稳健估计进行重点分析。

参考文献

[1] XI G U， LIAO Z. Short?term load forecasting based on phase space reconstruction and Gaussian process regression [J]. Power system protection & control， 2017， 45（5）： 73?79.

[2] LI C， LI S， LIU Y. A least squares support vector machine model optimized by moth?flame optimization algorithm for annual power load forecasting [J]. Applied intelligence， 2016， 45（4）： 1?13.

[3] RUI H， WEN S， ZENG Z， et al. A short?term power load forecasting model based on the generalized regression neural network with decreasing step fruit fly optimization algorithm [J]. Neurocomputing， 2016， 221： 24?31.

[4] BERNARD ?tienne， GABRIEL Pierre. Asymptotic behavior of the growth?fragmentation equation with bounded fragmentation rate [J]. Journal of functional analysis， 2017， 272（8）： 3455?3485.

[5] 仇瑞承，苗艳龙，张漫，等.基于线性回归的玉米生物量预测模型及验证[J].农业工程学报，2018，34（10）：131?137.

QIU Ruicheng， MIAO Yanlong， ZHANG Man， et al. Prediction model and verification of corn biomass based on linear regression [J]. Transactions of the Chinese society of agricultural engineering， 2018， 34（10）： 131?137.

[6] 薛斌，程超，欧世其，等.考虑舒适温度区间和突变量的月售电量预测线性回归模型[J].电力系统保护与控制，2017，45（1）：15?20.

XUE Bin， CHENG Chao， OU Shiqi， et al. Linear regression model for monthly electricity sales forecast considering comfort temperature range and sudden change [J]. Power system protection and control， 2017， 45（1）： 15?20.

[7] 冯敬海，朱骏桥.房价非线性回归模型及期权定价[J].大连理工大学学报，2017，57（5）：545?550.

FENG Jinghai， ZHU Junqiao. Nonlinear regression model of house prices and option pricing [J]. Journal of Dalian University of Technology， 2017， 57（5）： 545?550.

[8] PANDA S K， MOHANTY S N， JAGADEV A K. Long term electrical load forecasting： an empirical study across techniques and domains [J]. Indian journal of science and technology， 2017， 10（26）： 1?16.

[9] SONG K B， BAEK Y S， HONG D H， et al. Short?term load forecasting for the holidays using fuzzy linear regression method [J]. IEEE transactions on power systems， 2005， 20（1）： 96?101.

[10] LIU Weijiu. Asymptotic behavior of solutions of time?delayed Burgers′ equation [J]. Discrete and continuous dynamical systems—series B （DCDS?B）， 2017， 2（1）： 47?56.

[11] HANI Z， THOMANN L. Asymptotic behavior of the nonlinear schr?dinger equation with harmonic trapping [J]. Communications on pure & applied mathematics， 2016， 69（9）： 191?199.

[12] PAO C V. Asymptotic behavior of solutions for finite?diffe?rence equations of reaction?diffusion [J]. Journal of mathematical analysis & applications， 2017， 144（1）： 206?225.

[13] POTOMKIN Mykhailo. Asymptotic behavior of thermoviscoelastic Berger plate [J]. Communications on pure & applied analysis， 2017， 9（1）： 161?192.

[14] HUANG P， GAO G W， QIAN C S， et al. Fuzzy linear regression discriminant projection for face recognition   [J]. IEEE access， 2017， 5： 4340?4349.