五对角紧致差分格式优化及二维声波传播波动方程数值模拟

2019-08-12穆鹏飞蔡文杰桂志先

石油物探 2019年4期

汪勇,穆鹏飞,蔡文杰,王鹏,桂志先

(1.油气资源与勘探技术教育部重点实验室(长江大学),湖北武汉430100;2.长江大学地球物理与石油资源学院,湖北武汉430100;3.中海石油(中国)有限公司天津分公司,天津300450)

地震波场有限差分数值模拟[1-9]是研究复杂地区地震资料采集、处理和解释的有效辅助手段,也是逆时偏移和全波形反演的基础。紧致有限差分格式是其中一种具有较高计算效率的方法,与常规中心差分格式相比,它能够使用更少的计算节点达到相同的计算精度,减少了计算量和所需的存储空间。此外,紧致差分格式是一种隐式差分格式,使用该格式计算空间导数时,不仅用到了待求网格点周围的函数值,还用到了相邻节点的导数值,具有更低的数值频散误差,因而能够使用更粗的网格计算,提高数值模拟的计算效率。因此紧致差分格式被广泛应用于声波、弹性波和复杂介质等的地震波场数值模拟[10-17]。

在地震波场有限差分数值模拟中,需要高精度的空间离散差分算子。差分算子的精度取决于差分系数和差分阶数,差分阶数越高,差分算子越精确,差分精度就越高,数值频散越小,但其计算量也随之增大。优化差分系数可使差分算子最大程度地逼近空间偏导算子。KIM等[18]利用频散关系保持(dispersion-relation-preserving,DRP)的基本思想优化了一阶导数的紧致差分格式;LIU等[19]基于频散关系提出了优化的时空域有限差分系数,可在不增加计算成本的情况下显著提高模拟精度;ZHANG等[20-21]使用最大范数的目标函数及模拟退火算法求解目标函数,对一阶和二阶常规中心差分的差分系数进行了优化;LIU[22-23]使用最小平方法优化了二阶导数中心差分和一阶导数交错差分系数;YU等[24]基于DRP思想,优化得到了5阶精度的组合型紧致差分系数;REN等[25]利用优化后的时空域差分格式进行了声波和弹性波方程的数值模拟;YANG等[26]利用极小极大算法(minimax approximation)优化了交错网格差分系数,在保证中低波数范围内差分格式分辨率的同时,提高了大波数情况下的模拟精度。

本文首先将二阶导数的五对角紧致差分格式扩展到2N阶差分精度,然后基于频散关系保持的思想,根据最小平方法建立了波数误差的目标函数,利用拉格朗日乘数法对目标函数进行求解,得到了优化后的4～10阶精度差分系数。与KIM等[18]方法相比,除了优化目标是二阶导数以外,主要区别在于使用的方程和网格节点数不同,KIM等[18]方法在优化2～8阶精度差分系数时均使用了7个节点,而本文根据差分精度的不同,使用不同的节点数,提高了计算效率。最后,分析和对比了优化前后差分格式的模拟精度、数值频散和声波方程的稳定性条件,并应用优化后的紧致差分格式和基于辅助微分方程的完全匹配层边界条件对二阶声波方程进行了数值模拟,验证了方法的精度。

1 二维声波方程的高阶差分近似

根据弹性力学分析,二维情况下二阶声波方程(假设体力为零)可以表示为:

(1)

式中:u(x,z)为声波位移场;v(x,z)为声波速度场;x,z和t分别为空间和时间坐标。

1.1 时间2M阶近似

利用截断的泰勒公式表示n+1和n-1时刻的位移场可以得到:

式中:i,j和n分别为空间和时间网格坐标;Δt为时间步长。两式相加,略去高次项,得到位移场时间2M阶精度的差分格式:

(4)

当M=1时,根据声波方程((1)式),将(4)式中位移对时间的导数转化为位移对空间的导数,即可得时间二阶精度的差分格式:

(5)

当M=2时,同理可得时间四阶精度的差分格式:

(6)

公式(5)和公式(6)为位移场的三层显式差分格式,利用它们就可以进行地震波场时间层的推进计算。公式中含有位移u对x和z的二阶和四阶导数,这些导数将利用紧致差分格式进行求取。

1.2 空间2N阶紧致差分近似

1992年,LELE[27]对埃尔米特(Hermite)公式进行了扩展,构造了求解函数f(x)二阶导数的紧致差分格式为:

(7)

对公式(7)进行扩展,可以构造二阶导数的2N阶精度紧致差分格式。由于公式(7)左边有5项,系数矩阵为五对角矩阵,所以称为五对角紧致有限差分格式(pentadiagonal compact finite difference,简称CFD5),表示为:

(8)

从公式(8)可以看出,CFD5格式只需要利用2N-3个节点即可达到2N阶差分精度。利用泰勒级数展开和待定系数法以及下列方程组((9)式)可以求得CFD5格式2N(N≥3)阶差分精度的差分系数,表1列出了6～12阶精度CFD5格式差分系数。

(9)

利用公式(8)所表示的CFD5格式,可以求取公式(5)和公式(6)中的位移对空间的二阶偏导数∂2u/∂x2和∂2u/∂z2,差分格式写成矩阵形式为:

(10)

其中,

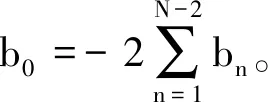
根据公式(10)即可求得空间二阶导数∂2U/∂x2和∂2U/∂z2的2N(N≥3)阶空间差分精度近似值,表示为:

(11)

此外,公式(6)中的四阶偏导数和混合偏导数,可以利用公式(11)对二阶偏导数再次求导进行求取。

表1 五对角紧致差分格式二阶导数的差分系数

2 二阶导数紧致格式的差分系数优化及分析

地震波场数值模拟中,为了得到清晰的波场记录,需要高精度的空间离散差分算子。精度越高的差分算子数值频散越小,但算子长度越大,计算量也越大。优化差分系数可使差分算子最大程度地逼近空间偏导算子,本节基于频散关系保持的基本思想,对二阶导数的紧致差分系数进行优化,提高紧致差分格式的分辨率。

2.1 优化差分系数

首先对CFD5格式(公式(8))进行数值频散分析,令:

(12)

将公式(12)代入公式(8)中可以得到(2N阶精度):

(13)

利用欧拉公式,并将B=-(k′)2A代入(13)式可得:

(14)

令ω=kh,ω′=k′h,则ω′可以表示为:

(15)

ω和ω′分别是真波数和数值波数与空间步长的乘积,在理想情况下,如果不存在数值频散,则ω′=ω。它们的差别越大,则说明该方法的数值频散越严重,反之则说明该方法能更好地压制数值频散。

下面以3点6阶格式为例来说明差分系数的优化方法。由公式(8)可以得到:

(16)

公式(16)中的差分系数a1,a2和b1为了满足2阶和4阶精度泰勒公式截断误差的要求,必须满足方程组:

(17)

按照TAM等[28]提出的DRP思路,在某个选定的波数范围内,确定公式(17)中的3个未知差分系数a1,a2和b1,使得数值波数k′尽可能地接近真波数k。为了消除数值波数表达式中的根号,简化计算,定义误差函数为:

(18)

其中,W(ω)为一个加权函数,目标是使误差函数解析可积,它是ω2-ω′2的分母部分。θ是积分上限,取值范围是θ∈(0,π),取值大小与差分精度有关,一般低阶取小值,高阶取大值。它的取值不同,计算出来的差分系数也不同,这里θ=5π/8。

选定a1为变量,由方程(17)可得b1=(36a1+24)/23,a2=(1-10a1)/46。确定E的最小值为条件极值问题,采用拉格朗日乘数法进行求解,即根据∂E/∂a1=0,可以得到:

(19)

由公式(17)、公式(18)和(19)可以确定3个优化后的差分系数,a1=0.127658,a2=-0.006013,b1=1.243290。将上述差分系数代入公式(8),则得到优化后的4阶精度五对角紧致差分格式(pentadiagonal optimized compact finite difference,以下简称OCFD5)。采用同样的方法,对公式(8)表示的CFD5格式进行差分系数优化,优化后的4～10阶差分系数见表2。为了方便,将二阶导数的2N阶精度优化前后的紧致差分格式统一表示为:

(20)

CFD5:L=N-2,N≥3,a1,a2和bl见表1。OCFD5:L=N-1,N≥2,a1,a2和bl见表2。

若要达到2N阶空间差分精度,优化前的CFD5方法需要利用2N-3个节点,优化后的OCFD5方法需要使用2N-1个节点。

表2 二阶导数的五对角优化紧致差分格式的差分系数

由于不同的积分上限可以得到不同的差分系数,这里补充说明积分上限选取的原则。通过选取θ=3π/8～7π/8,可以得到不同的差分系数,表3为4阶精度差分格式优化时,不同积分上限时得到差分系数。由不同的差分系数可以得到各自的波数比曲线,如图1所示,其中波数比定义为数值波数与真波数之比,表示为R=k′/k=k′h/kh=ω′/ω。

由4阶精度格式优化结果可以看出(图1a),当θ=5π/8,波数比曲线接近1的范围最大。θ取值较小时,有效的波数范围较小,达不到优化的目的;θ取值过大时,曲线向上偏离1,也会造成数值频散。定量来看,若给定频散误差标准E=|R-1|≤0.2%,当积分上限θ=3π/8,4π/8,5π/8,6π/8,7π/8时,波数比R满足误差标准的最大ω分别为1.55,1.69,1.92,1.12和0.96。也就是说,当θ=5π/8时的满足误差标准的波数范围最宽,能在最大的范围内压制数值频散。图1b到图1d是6,8,10阶OCFD5格式在不同积分上限时得到的波数比曲线,与4阶精度时确定积分上限和对应优化系数的原则类似,确定6阶和8阶时的积分上限θ=6π/8,10阶时的积分上限θ=7π/8。由于篇幅所限,6～10阶不同积分上限时的差分系数不具体列出。

2.2 频散分析

CFD5格式和OCFD5格式的数值波数与真波数之比R可以表示为:

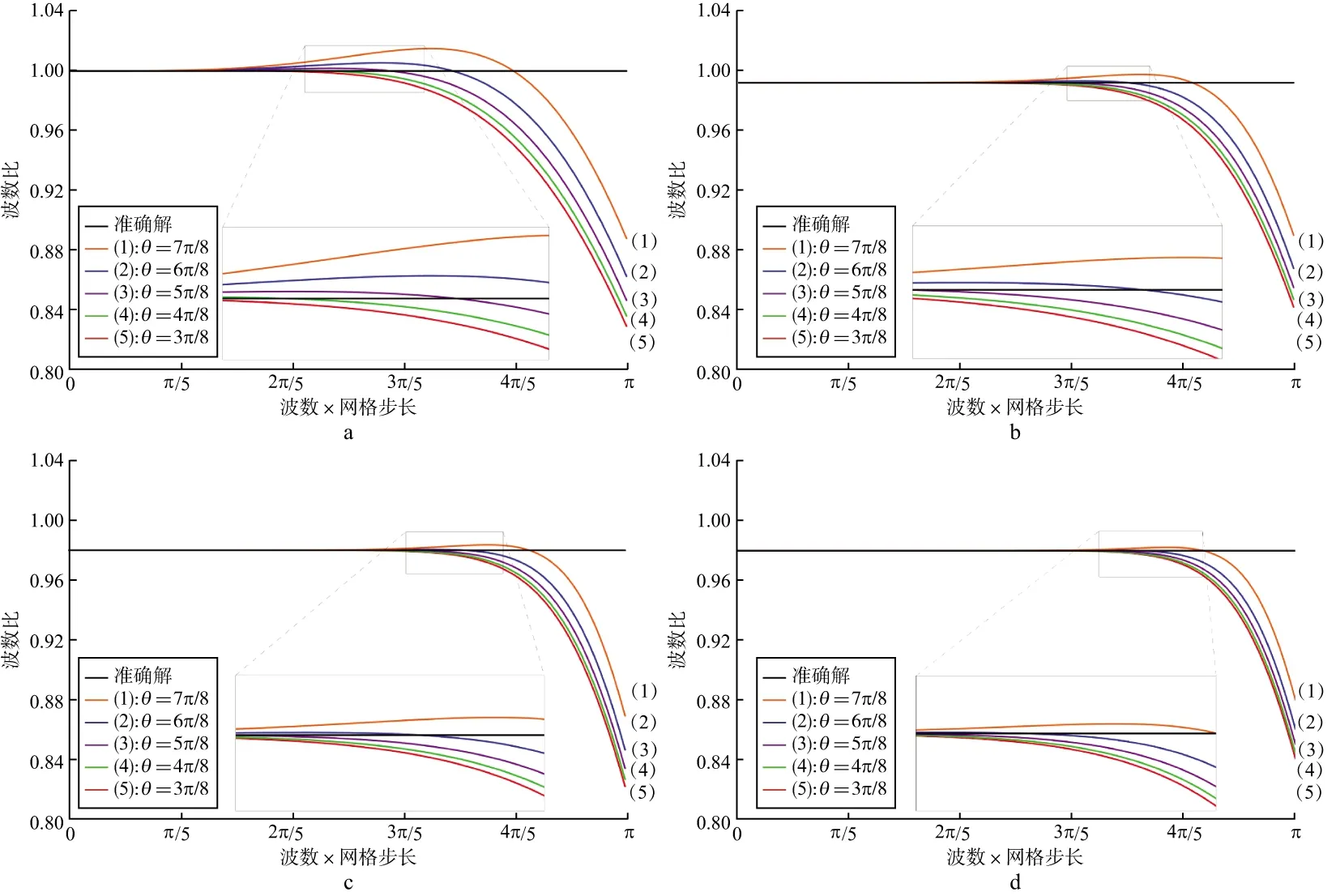
图1 不同积分上限θ优化后格式的波数比曲线a 4阶精度; b 6阶精度; c 8阶精度; d 10阶精度

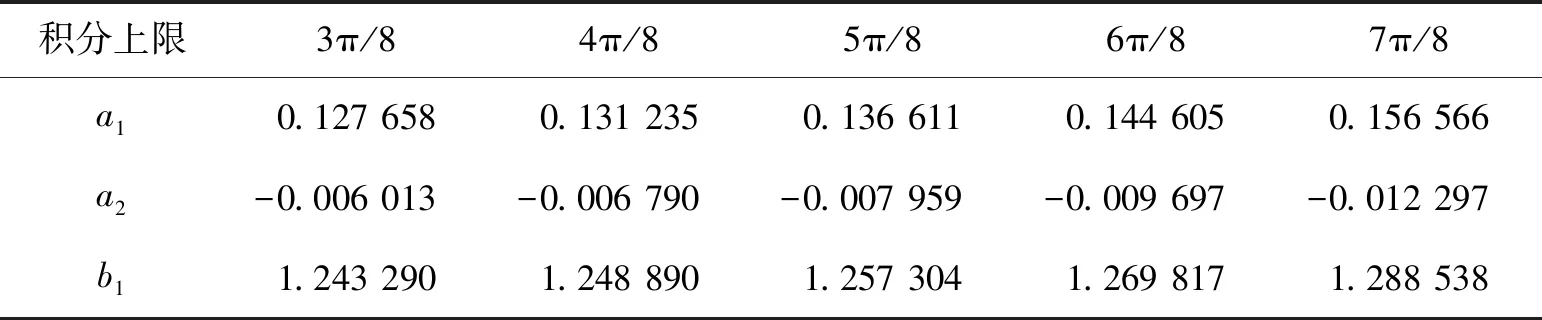
积分上限3π/84π/85π/86π/87π/8a10.1276580.1312350.1366110.1446050.156566a2-0.006013-0.006790-0.007959-0.009697-0.012297b11.2432901.2488901.2573041.2698171.288538

(21)

在理想情况下,即不存在数值频散时,R恒等于1。R偏离1越大,说明该方法的数值频散越严重,反之则说明该方法能更好地压制数值频散。使用表1和表2中不同精度的差分系数,可以计算得到CFD5和OCFD5格式的波数比曲线,如图2所示。

由图2波数比曲线可以看出:①在相同的差分精度情况下,优化后的格式比优化前的波数比曲线更接近1,所以每个波长内需要的最少采样点数更少,这说明优化过程起到了提高压制数值频散的作用,数值计算时能使用更大的空间网格,从而减少了计算内存,提高了计算效率;②优化后的2N阶精度格式,波数比曲线比2N+2阶精度优化前的频散误差更小,例如图2a中的4阶OCFD5要好于6阶的CFD5。由图2b到图2d也可以得出相同结论。

2.3 差分精度分析

进行数值模拟时,在时间差分精度相同的条件下,不论是利用优化前的CFD5格式,还是利用优化后的OCFD5格式,它们在时间层递推方式上是相同的,不同之处仅在于空间偏导数近似值求取时的差分格式不同。为了比较它们的近似精度,需要对其截断误差进行对比,结果见表4。从表4中可以看出,在两种方法达到同样空间近似精度的条件下,优化后的格式具有更小的截断误差,例如6阶精度时的CFD5截断误差约为OCFD5的3.69倍。

利用一维平面简谐波初值问题的解析解来比较优化前后格式的数值模拟精度。一维平面谐波初值问题可以表示为:

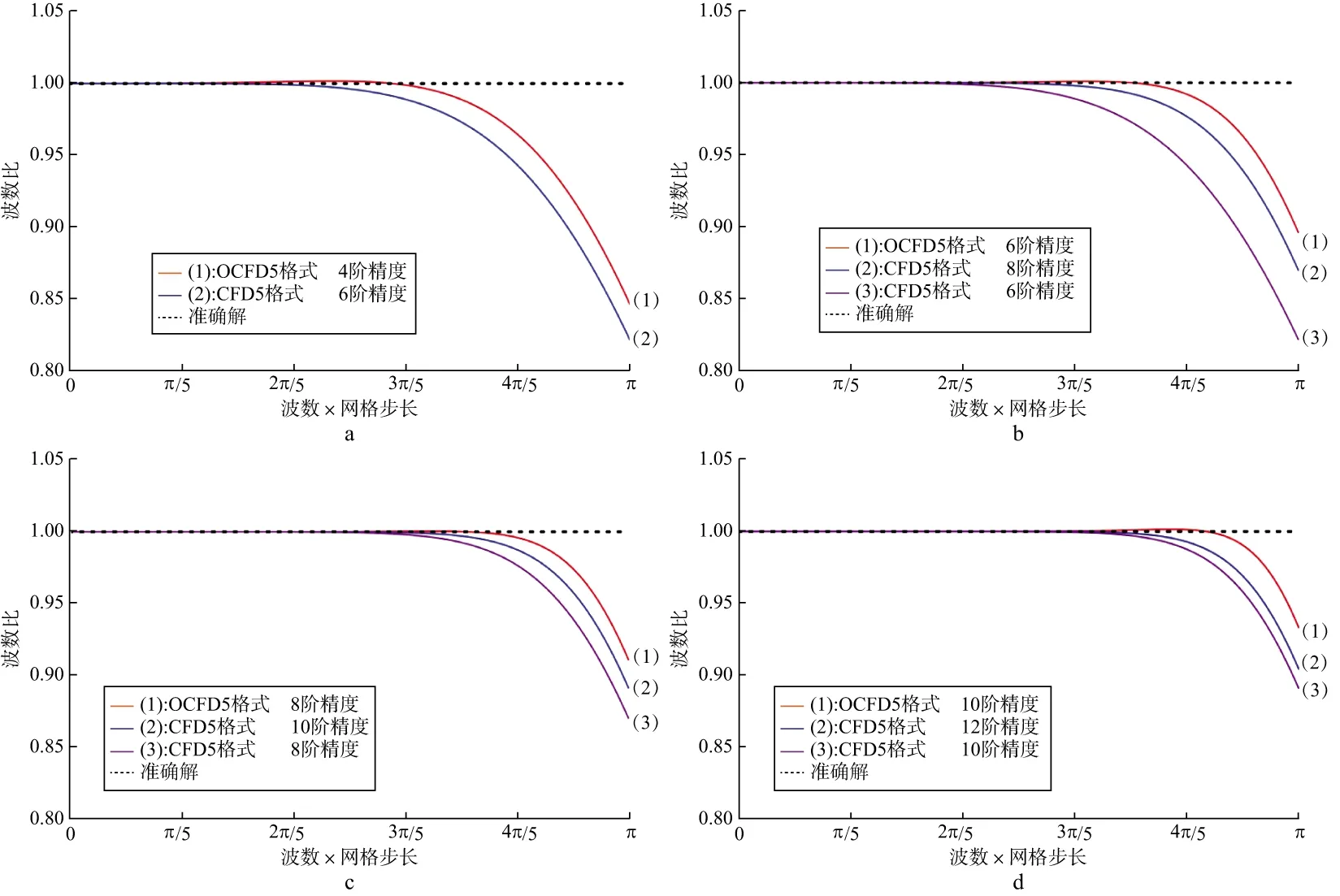
图2 不同差分精度时CFD5和OCFD5格式的波数比曲线a 4阶和6阶精度比较; b 6阶和8阶精度比较; c 8阶和10阶精度比较; d 10阶和12阶精度比较

表4 优化前后格式的二阶导数截断误差主项系数比较

(22)

式中:v是平面波的波速;f0是平面简谐波的频率。

其初值问题的解析解为:

(23)

设置一维介质模型长度8km,平面波速v=2000m/s,f0=10Hz,数值模拟时的时间步长2ms,空间网格大小20m。数值模拟时,两种差分格式均为时间4阶、空间6阶精度。通过数值模拟,可得图3 所示的1s时刻的位移u的波场快照,图中蓝色实线是用公式(23)计算得到的精确解析解。从图3可以看出,两种差分格式模拟精度均很高,图3a中的3条曲线基本重合,无明显误差。但从局部放大的图3b 和图3c来看,优化后的OCFD5格式的数值模拟结果与精确的解析解更接近,说明优化格式的模拟精度得到了提高。

为了避免边界反射的影响,定量计算得到1s时刻3000～5000m区间的CFD5和OCFD5数值解与解析解之间的相对误差分别为0.1005%和0.0167%。这是由于它们在计算空间导数近似值时存在不同截断误差大小造成的,这与表4的理论分析结果一致。相对误差定义为:

(24)

图3 一维声波方程数值模拟快照a 3000～5000m范围的波场快照; b 图3a中A部分放大显示; c 图3a中B部分放大显示

2.4 稳定性条件

稳定性条件是有限差分数值模拟中一个非常重要的问题,是影响差分方法计算效率的重要因素。我们采用Fourier方法对公式(5)表示的二维声波方程的时间2阶、空间2N精度差分格式进行稳定性分析。

定义:

(25)

式中:kx和kz为x和z方向的视波数;i,j和n分别为空间和时间网格坐标;ξ和ζ1为振幅。代入公式(20)中可得:

(26)

令θ1=kxh,-π/2≤θ1≤π/2,并利用欧拉公式,将(26)式化简可得:

(27)

解方程可得:

(28)

同理,对于z方向,定义:

(29)

代入公式(20)同样可以得到:

(30)

公式(5)是一个三层显式差分格式,为了分析其增长矩阵,将其改写为:

(31)

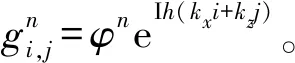
(32)

若使差分格式(32)满足稳定性条件,则增长矩阵G最大特征值的模不大于1,由此可得稳定性条件为:

(33)

由公式(28)和公式(30)可以得到:

(34)

所以二维声波方程的时间2阶、空间2N阶精度差分格式的稳定性条件可写为:

(35)

式中:Δt为时间步长;h为空间网格大小;v为地震波速度;a1,a2和bl为表1和表2中的紧致差分格式差分系数。

定义α=vΔt/h,稳定性条件写作α≤C(C称为Courant数),声波方程时间2阶精度的CFD5和OCFD5格式的稳定性条件如表5所示。从表5来看,C随时间差分精度的增加而增加,随空间差分精度的增加而减小。在同样的差分精度条件下,优化后格式的稳定性条件比优化前要略微严格,也就是说在相同空间步长时,允许的时间步长要略小。声波方程时间4阶精度的稳定性条件很难给出具体表达式,表5 给出的不同情况下的稳定性条件是根据试验获得的。

2.5 边界条件

在数值模拟时,由于模型的设置和计算模型大小的限制,必然会存在人工边界。如果不对人工边界进行处理,边界反射会干扰正常的地震波场,所以人工边界的处理直接影响到数值模拟的精度和效率。1994年,BERENGER[29]提出的完全匹配层(perfectly matched layer,简称PML)能对边界反射起到很好的吸收作用。在此基础上,DROSSAERT等[30-31]提出的复频移完全匹配层(complex frequency shifted perfectly matched layer,简称CFS-PML)能对近掠入射的低频波起到更好的衰减作用,而卷积PML[32](convolutional PML)和辅助微分方程PML[33](auxiliary differential equation PML,简称ADE-PML)的优点是可以使用非分裂的波动方程。针对二阶声波方程,本文采用辅助微分方程结合复频移完全匹配层[34](ADE-CFS-PML)进行边界处理,略去推导过程,直接给出x方向控制方程为:

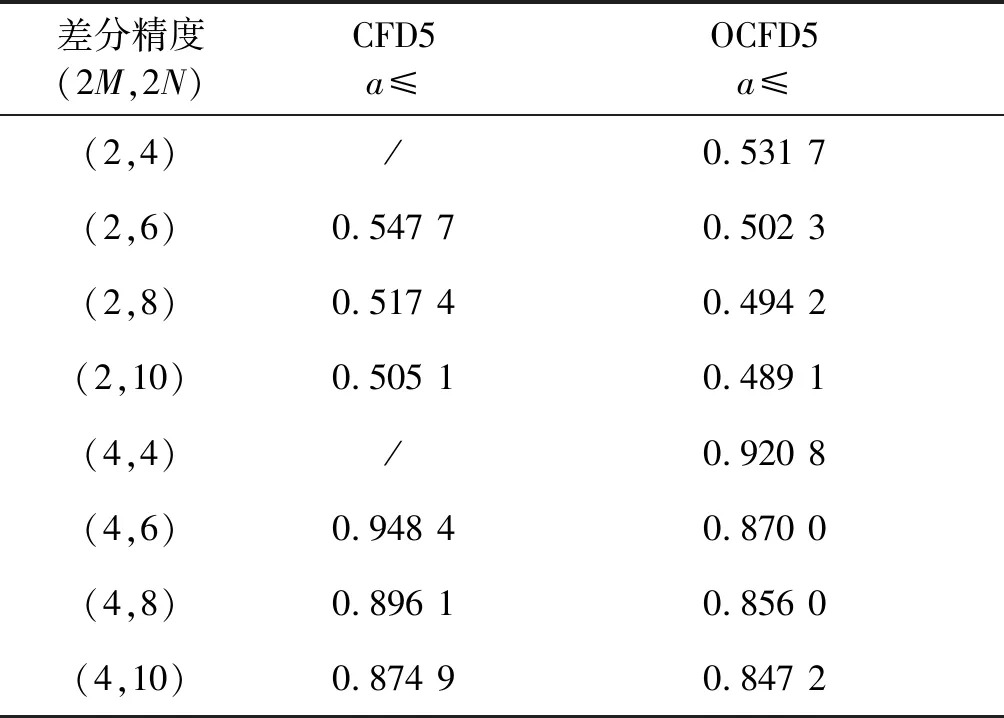
表5 二维声波方程优化前后紧致差分格式的稳定性条件

(36)

式中:u1,u2和u3是引入的中间变量,可由(36)式中第一个方程到第三个方程依次计算u3,u2和u1;参数α′和d′分别是α(x)和d(x)对x的一阶导数。α(x)和d(x)表示为:

(37)

式中:d(x)是x方向的衰减系数,起到衰减x方向波的作用;αmax=πf0,f0是震源信号主频;δ是PML边界厚度;x是节点至PML最内层边界的距离。此外,d0=[3vmaxln(1/F)]/(2δ)[35],vmax是地震波传播的最大速度,F是理论反射系数,表示为lgF=[1-lgN]/lg2-3,N是PML边界层数,本文N=20。

公式(36)只表示了x方向的控制方程,同样方法可以得到z方向的控制方程,文中不再赘述。

3 模型试算

3.1 均匀介质模型

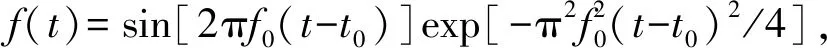
由图4可以看出:①当使用相对较粗网格计算时,图4a所示的6阶CFD5格式的波场快照频散严重,与2.2节的理论分析结果一致;②增加网格点数和差分阶数后,图4b所示的8阶CFD5格式的波场快照的频散得到了压制,但频散还是较为明显;③图4c 所示的6阶OCFD5格式的波场快照数值频散明显减弱,模拟结果不仅优于优化前同阶精度的图4a,也好于差分精度更高的图4b;④图4d所示的8阶OCFD5格式的波场快照清晰,波形光滑,无明显数值频散。优化前后波场快照的比较结果,说明了本文基于DRP思路进行优化的结果达到了压制数值频散的目的。

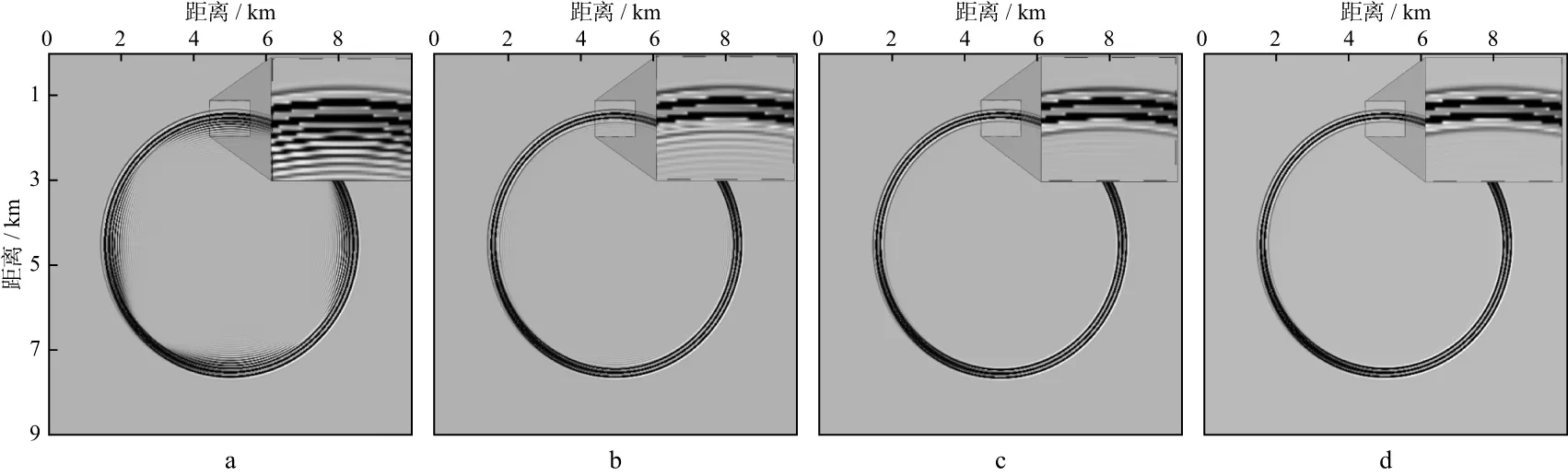
图4 不同差分格式计算的1000ms时刻波场快照a CFD5 (4,6); b CFD5 (4,8); c OCFD5(4,6); d OCFD5(4,8)

基于该模型进行计算效率分析,结果如表6所示。表6中所取空间网格大小满足波场快照无数值频散要求,同时为了简化分析和避免时间步长过大产生的数值频散,时间步长均为3ms。4种格式的数值模拟没有本质的差别,计算中需要的变量(数组)个数一样,只是差分系数和算子长度不同,它们均在相同的运行环境和程序下进行数值模拟。从表6中可以看出,优化后的格式由于能使用更粗的网格计算,所以单个变量的网格数降低,既减少了内存的占用,也减少了计算时间,从而提高了数值模拟的计算效率。

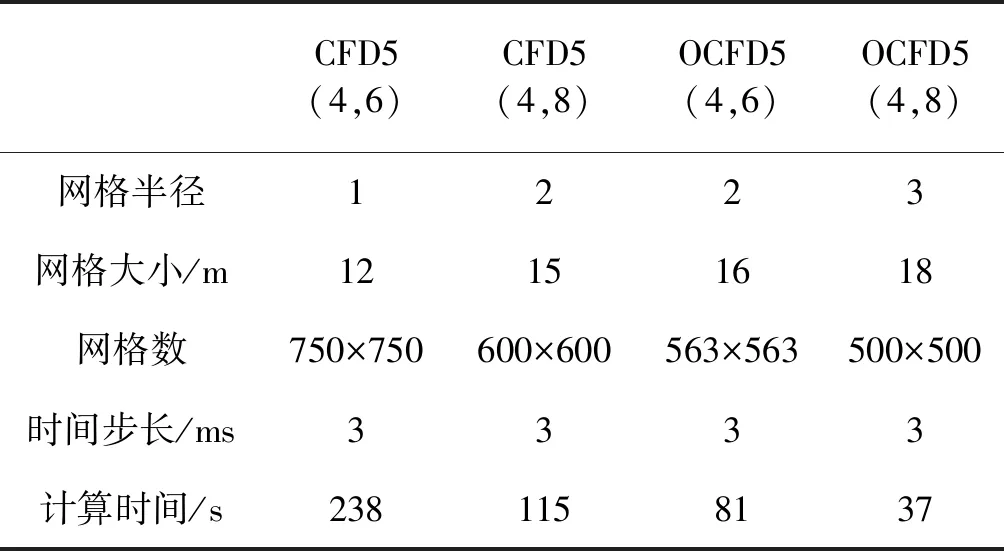
表6 不同方法计算效率比较

3.2 Marmousi模型

为了验证优化后的紧致差分格式对复杂介质的适用性,用经典的二维Marmousi纵波速度模型进行数值模拟。模型如图5所示,速度v的范围是1729～5500m/s。模型大小为501×501个网格点,空间网格12m,时间步长1ms,震源位于(x=3000m,z=0)位置,激发震源采用30Hz的Ricker子波,采样时间4s,利用ADE-CFS-PML边界条件对人工边界反射进行吸收处理。

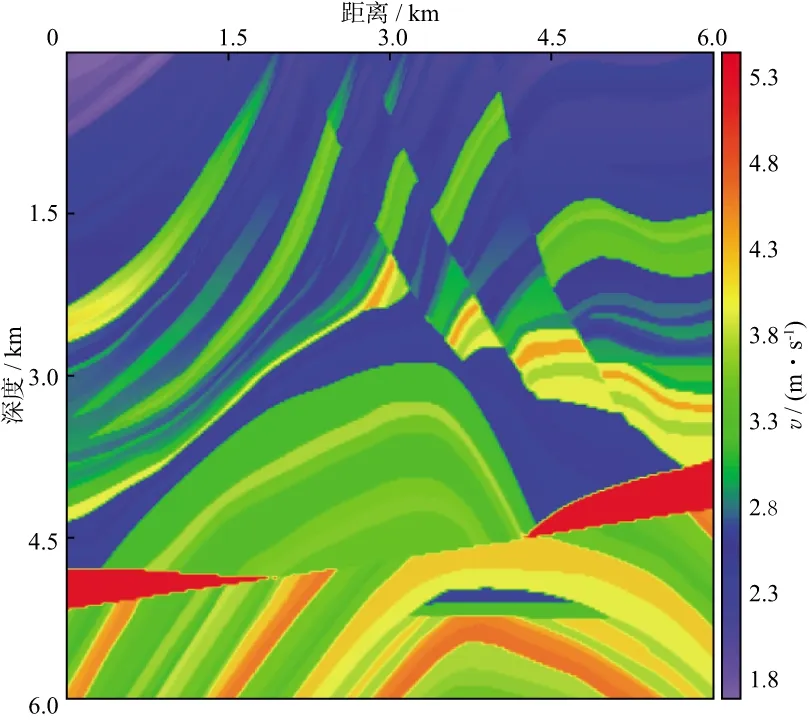
图5 Marmousi纵波速度模型

图6给出了采用OCFD5(2,6)格式对Marmousi模型进行声波方程数值模拟得到的不同时刻的波场快照。从图6可以看出,Marmousi模型中地震波场复杂且清晰,能够反映地震波的传播特征。同时,边界反射吸收效果较好,无明显边界反射,说明本文差分方法在ADE-CFS-PML边界条件下,对边界反射起到了很好的衰减作用。

图7是分别使用优化前后格式得到的地震记录,精度均为时间2阶、空间6阶。为了显示清晰,对地震记录进行了瞬时自动增益控制(AGC)处理,时窗2s。

从图7中方框所示范围内的地震波场来看,优化前CFD5格式的数值模拟结果出现了较严重的数值频散,干扰了正常的地震波场,不利于波场特征分析及其它处理;而优化后OCFD5格式的数值模拟结果,模拟精度高,无明显数值频散。同时,直达波、反射波及绕射波等波型清晰可见,且边界吸收效果较好,无明显边界反射,验证了本文算法对复杂模型的适用性。