自适应加权混合L1/L2范数匹配相减多次波压制方法

陈习峰,薛永安,黄新武

(1.中国石油化工股份有限公司江苏油田分公司物探研究院,江苏南京210046;2.中国地质大学工程技术学院,北京100083)

多次波是海洋和陆地地震勘探中面临的突出问题,它严重降低了地震资料的品质,影响了地下地质体成像的真实性和可靠性,干扰了后续的地震资料解释,因此解决多次波的压制问题对油气勘探意义重大。

为了较好地压制多次波,地球物理工作者研究了大量方法技术。WEGLEIN[1]将多次波压制的方法分为两类:一类是基于有效波和多次波之间动力学和运动学差异的方法,简称滤波方法;另一类是基于波动方程的预测相减法,简称波动方程预测减去法,即利用波动方程模拟实际波场或反演地震数据预测多次波,再将多次波从原始地震数据中减去的方法。陈祖传[2]将多次波的压制技术分为3类:第1类是利用一次波与多次波正常时差的差异,如共中心点叠加法、滤波法、变换样点调序法等;第2类是多次波模型减去法,如波场外推法、表层多次波衰减法等;第3类是利用多次波的重复性和统计性去除多次波,此类方法利用多次波周期重复出现的统计特性,根据预测算子来消除多次波,如预测反褶积法。

目前较先进的压制多次波方法是基于波动方程的预测相减法,根据地震数据预测多次波模型记录,再采用自适应匹配相减方法减去多次波,达到多次波压制的目的[3-4]。最典型的预测相减方法为与自由表面相关的多次波压制算法,该方法适用于复杂地下结构,并且无需地下结构的先验信息,压制多次波时采用了常规的最小二乘自适应匹配相减方法[5-9]。WANG[10]提出了扩展多道匹配方法,李鹏等[11-12]提出了均衡拟多道匹配相减方法,这两种方法均对常规的匹配相减方法进行了较大改进,衰减自由表面多次波效果良好。上述预测相减法主要基于L2范数。理论上,一次波与多次波正交时,基于L2范数自适应匹配相减方法(简称L2范数方法)可有效地消除多次波。但一般情况下,一次波与多次波不正交,此时采用自适应匹配相减方法压制多次波效果差,而且有可能损害有效波。为此,孙维蔷等[13]提出了一种相似系数谱约束的多次波自适应匹配相减方法,并取得一定效果。

2004年,GUITTON等[14]提出了基于L1范数的多次波自适应匹配相减方法(简称L1范数方法),该方法在数据中存在较大异常值时也能给出稳定解,且无须满足有效波与多次波正交这一假设条件,因而可以利用L1范数代替L2范数建立多次波自适应匹配相减滤波器。但是基于L1范数的目标函数的一阶导数不是处处连续,因此不能采用高效的莱文森递推算法求解,需采用非线性反演方法来确定最优的匹配滤波器,这给目标函数求解带来了困难。尽管采用迭代加权最小二乘(iterative reweighted least squares,IRLS)算法可近似求解基于L1范数的非线性问题,但求解过程较L2范数方法复杂得多,计算量显著增加。

形成多次波的地质条件复杂多样,实际地震资料不仅包括自由表面相关多次波,还包括层间多次波,波场的复杂特性使其通常不完全满足L2范数或者L1范数的假设条件,有效波与多次波的能量对比随时间和空间变化差别大,如果单独应用一种方法压制多次波,可能会导致较强的多次波能量剩余或计算效率较低,甚至可能压制部分有效信号。本文提出了一种自适应加权混合L1/L2范数多次波匹配相减方法,可以利用L1范数和L2范数方法的优点,并避开L1范数和L2范数方法的缺点。将该方法应用于多层水平层状模型及SEG/EAGE Pluto模型的多次波压制,验证了方法的有效性。

1 方法原理

L2范数方法是目前应用最广泛的一种方法,该方法基于剩余能量最小准则,假定地震有效波具有最小能量。基于L2范数求取匹配滤波算子为f时的目标函数Q2(f)为:

(1)

式中:M是预测多次波模型;d为原始含多次波地震数据。

当有效波与多次波不正交,或在最小二乘意义下有效波不具有最小能量时,L2范数方法应用效果不佳,会剩余较多的多次波能量,甚至损害一次波。

采用L1范数方法对数据中的异常值或者大振幅异常处理结果稳健[15],如果原始数据的有效波能量强,可将数据中的有效波能量看作异常值,利用L1范数方法进行处理。基于这种假设,GUITTON等[14]提出了基于L1范数求取匹配滤波算子f的方法,其目标函数Q1(f)为:

(2)

方程(2)是奇异的,因此在目标函数最小化时必须采用特殊技术来最小化或者近似代替L1范数[16-17]。IRLS算法可近似代替L1范数[18-19]。此时,重新定义目标函数为:

(3)

式中:算子W为加权矩阵,是剩余误差的函数。

(4)

i=1,2,…,N

式中:ε为先验值参数,ε=max|d|/100;ri为第i个采样点去除多次波后的残差。基于特定的W,最小化Q1(f):

(5)

式中:N为数据样点数。利用能量最小化原则,对于任意的ri,可以得到:

(6)

可以看出,当ri较小时,求解的是L2范数解,而当ri较大时,求解的是L1范数解。目标函数的最小二乘解的方程组如下:

(7)

目标函数(3)的最优化过程是非线性的。IRLS算法作为一种非线性优化技术,采用分步线性的方法来求解非线性问题。当地震有效波与多次波的能量比随空间和时间变化时,仅采用基于L2范数或者L1范数的多次波自适应匹配相减方法可能会造成一次波损害,运算速度降低或者多次波压制效果不佳。为此,熊繁升等[20]引入了一种混合范数方法,它利用加权系数将两种范数的目标函数组合,定义如下:

(8)

式中:λ为自适应加权系数;‖·‖1表示L1范数;‖·‖2表示L2范数。

采用迭代加权最小二乘算法将(8)式的目标函数Q(f)重新定义为:

(9)

采用最小二乘算法,得到的混合目标函数为:

(10)

将得到的加权矩阵W,加权系数λ,原始地震数据d,以及预测多次波模型M代入(10)式,求得最优匹配算子f。

实际地震数据中有效波与多次波能量比随空间和时间变化,为了保持地震有效波不受损害,必须自适应地确定加权系数λ。为此,我们研究出一种完全由数据驱动,并且根据实际地震有效波与多次波能量之比随空间和时间变化的情况自适应地确定加权系数λ的方法。

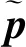
(11)

自适应匹配后的多次波定义如下:

(12)

在自适应匹配处理的时间-空间窗口内,定义地震有效波与多次波能量比为PMR:

(13)

根据公式(13),可自适应地定义加权系数λ:

(14)

自适应加权系数λ具有如下特点:

1) 能量比PMR为0～∞,根据方程(14),加权系数λ为0～1。

2) 根据方程(13),当PMR≫1时,地震有效波能量远大于多次波能量,极限情况是PMR为∞,即时窗内不存在多次波。此时不满足基于最小能量准则的假设条件,不适用L2范数方法求解,宜采用L1范数方法求解。在此情况下,根据方程(14)定义的加权系数λ趋近于0,代入方程(9),此时的目标函数正好趋近于L1范数方法的目标函数。

3) 根据方程(13),当PMR≪1时,地震有效波能量远小于多次波能量,极限情况是PMR=0,即时窗内无有效波。此时完全满足基于最小能量准则的假设条件,适用L2范数方法求解。在此情况下,根据方程(14)定义的加权系数λ趋近于1,代入方程(9),目标函数趋近于L2范数的目标函数(1)。

2 模型测试

2.1 二维模型测试

设计的5层水平层状模型见图1a;图1b和图1c分别为采用有限差分法模拟的不含自由表面多次波和含自由表面多次波的叠前炮集数据。选取两个时窗(0～1.2s)和(1.2～2.0s)分析PMR随炮检距的变化情况,结果如图1d和图1e所示。分析发现,PMR随时间和空间的变化大,浅层部分以有效波为主,适宜采用L1范数方法求解;中、深层部分有效波与多次波能量相当,甚至相对更弱,适合采用混合范数优化方法或L2范数方法求解。

图2a是原始的含自由表面多次波的炮集记录;图2b 是采用L2范数方法压制多次波后的单炮记录,很明显由于原始数据不满足其假设条件,应用效果较差;图2c是采用L1范数方法压制多次波的结果,应用效果较好,但浅部大偏移距处多次波压制效果不佳,从图1d 可知,浅部大偏移处的数据更符合L2范数的假设条件。图2d是采用本文提出的自适应加权混合L1/L2范数匹配相减方法压制多次波后的单炮记录,可以看出,该方法得到的结果明显优于L2范数方法得到的结果,计算效率比图2c中的L1范数方法提高了1.2倍。

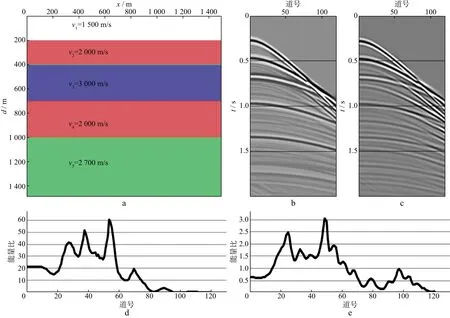
图1 二维水平层状模型数据分析结果a 速度模型; b 不含自由表面多次波的单炮记录; c 含自由表面多次波的单炮记录; d 时窗0～1.2s内PMR随炮检距变化曲线; e 时窗1.2～2.0s内PMR随炮检距变化曲线

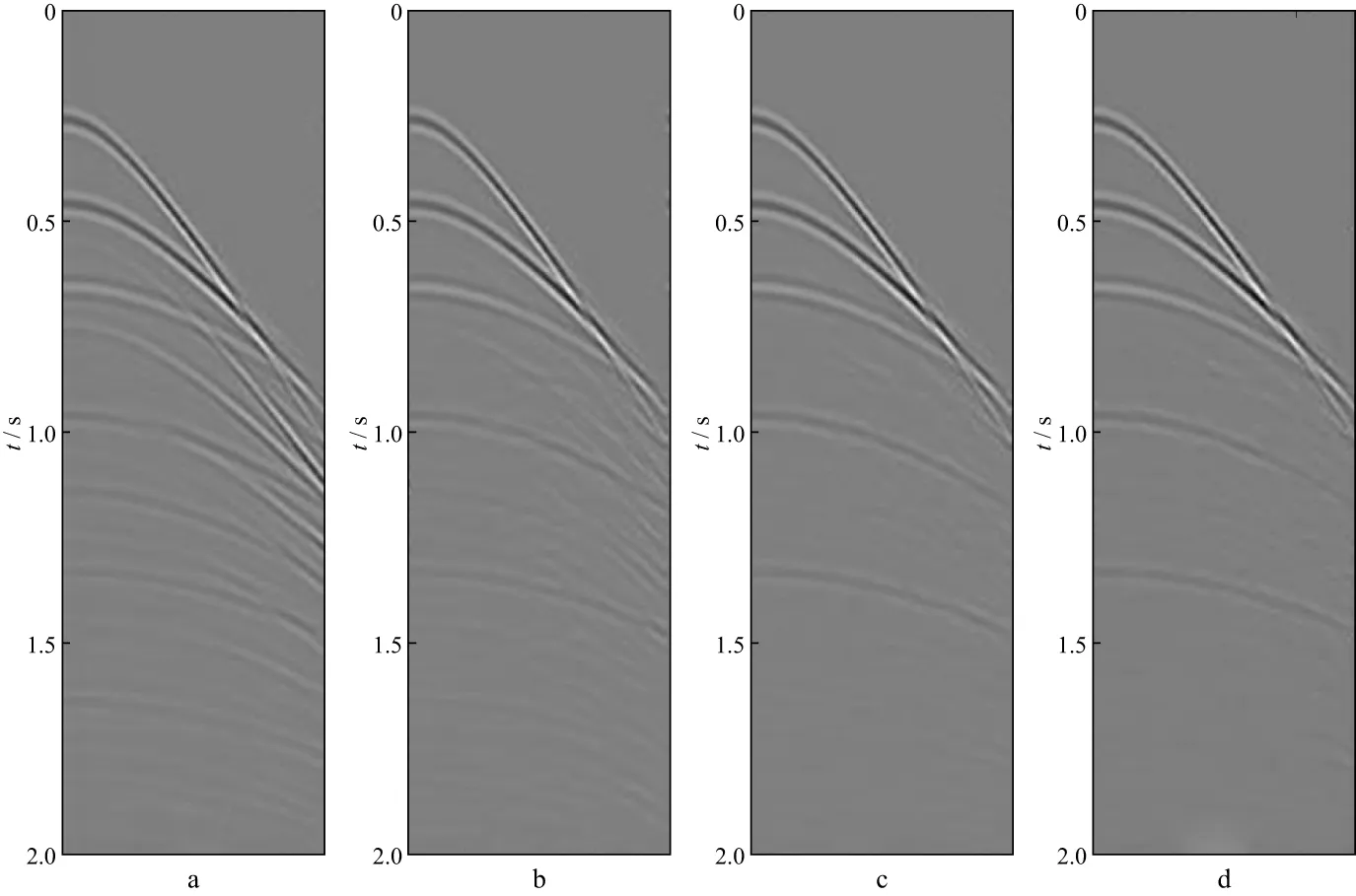
图2 原始单炮记录和采用不同方法压制多次波后的单炮记录a 原始单炮记录(含多次波); b L2范数方法; c L1范数方法; d 本文方法

2.2 三维模型测试

图3为5层水平层状介质三维深度域速度模型,层速度与图1的参数相同,但无基底速度,采用声波方程的三维有限差分法人工合成地震记录,对模型边界分别采用吸收和反射边界条件处理。

采用主频为20Hz的零相位Ricker地震子波,数据采集为三维固定排列放炮观测系统,每炮包括51条接收线,接收线距20m,每条接收线包括51个接收点,接收点距20m,每炮包括2601个接收点,排列内最小偏移距为0,时间长度为1500ms,时间采样间隔为4ms,炮点和检波点间距均为20m,炮线距20m。炮点与检波点完全重合,一共包括51条激发炮线,每条炮线包括51个炮点,共模拟了2601炮记录,激发时接收排列固定不变。

图4a为模拟的原始单炮记录(含多次波),图4b为采用三维波动方程方法预测的y方向的多次波贡献道集(MCG),图4c为MCG道集叠加后采用三维波动方程方法预测的单道多次波的结果,红色竖线代表选取炮集上的某一道,红色横线是为了便于对比相同时刻的地震波场对比。

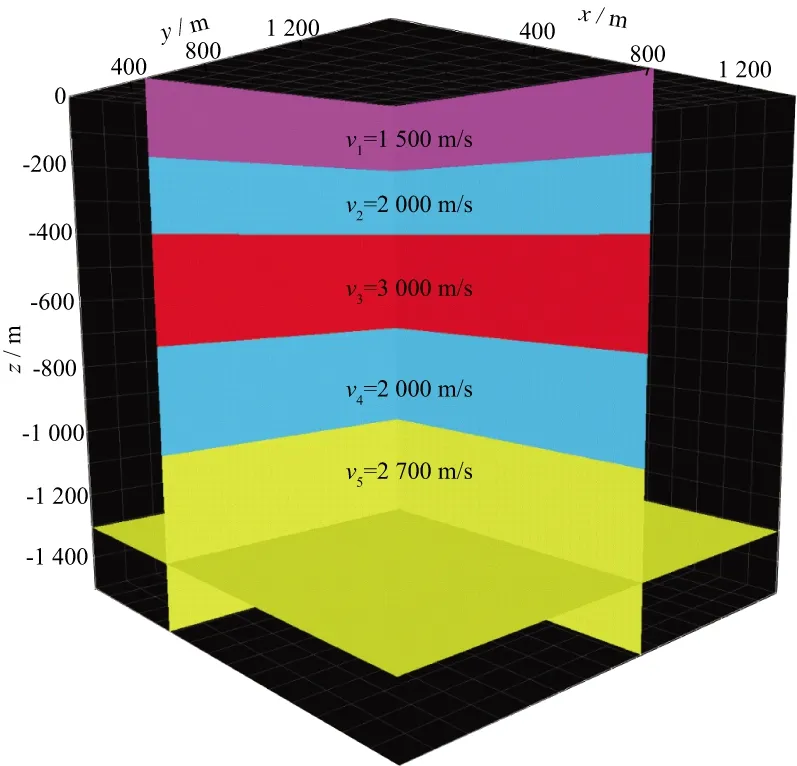
图3 5层水平层状介质三维深度域速度模型

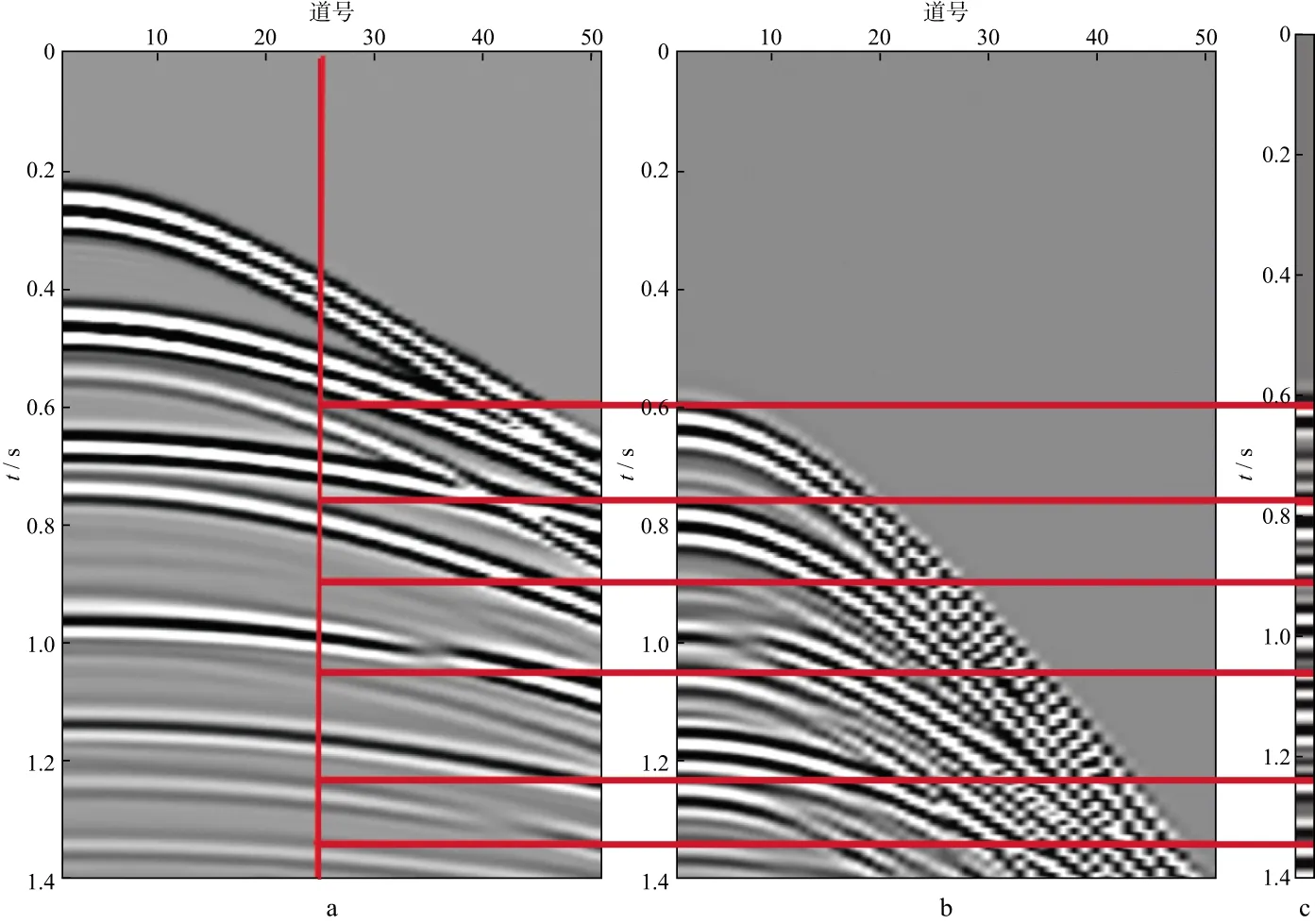
图4 预测多次波的单道示例a x=0,y=0位置处的单炮记录; b 预测的MCG道集; c MCG道集叠加后预测的单道多次波

图5展示了图3模型所示的双层旅行时,267ms时出现第1反射界面的同相轴,467ms时出现第2反射界面的同相轴,667ms时出现第3反射界面的同相轴,967ms时出现第4反射界面的同相轴。

图6a为模拟的原始单炮记录(含多次波),结合图5的双层旅行时,确定了各反射界面的反射波和多次波;图6b为采用波动方程方法预测的多次波,图6c为采用本文方法压制多次波后的单炮记录。可以看出,本文方法对层间多次波的压制效果好,尤其是近偏移距处压制效果较好,但远偏移距处的压制效果仍有待改进。

图7为原始数据剖面与压制多次波后得到的零偏移距剖面。与含多次波的原始数据剖面相比,采用本文方法压制多次波后得到的零偏移距剖面中包括层间多次波在内的绝大部分多次波能量已得到了有效压制。

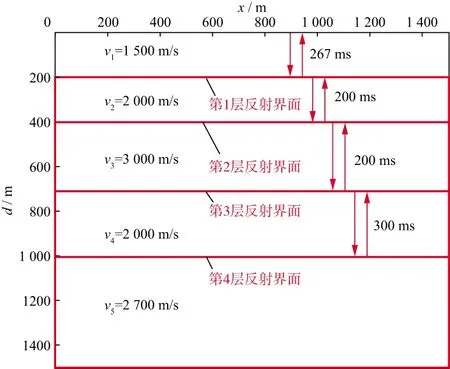
图5 水平层状介质模型各层的双层旅行时

图8分别为采用本文方法、L1范数和L2范数方法压制多次波后得到的叠加剖面,其中图8a为原始数据剖面,图8b为采用L2范数方法压制多次波后得到的叠加剖面,图8c为采用L1范数方法压制多次波后得到的叠加剖面,图8d为采用本文方法压制多次波后得到的叠加剖面。可以看出,L2范数方法对多次波压制效果差,L1范数方法虽然压制多次波效果好,但一定程度上损害了有效信号,采用本文方法不但较好地压制了多次波,还较好地保护了有效信号。

2.3 Pluto模型测试

图9为SEG/EAGE提供的Pluto速度模型。该模型的浅层为海水层,速度为1500m/s,盐丘的速度为4500m/s,因此正演模拟数据中,存在强烈的海水面与海底间反射的多次波。

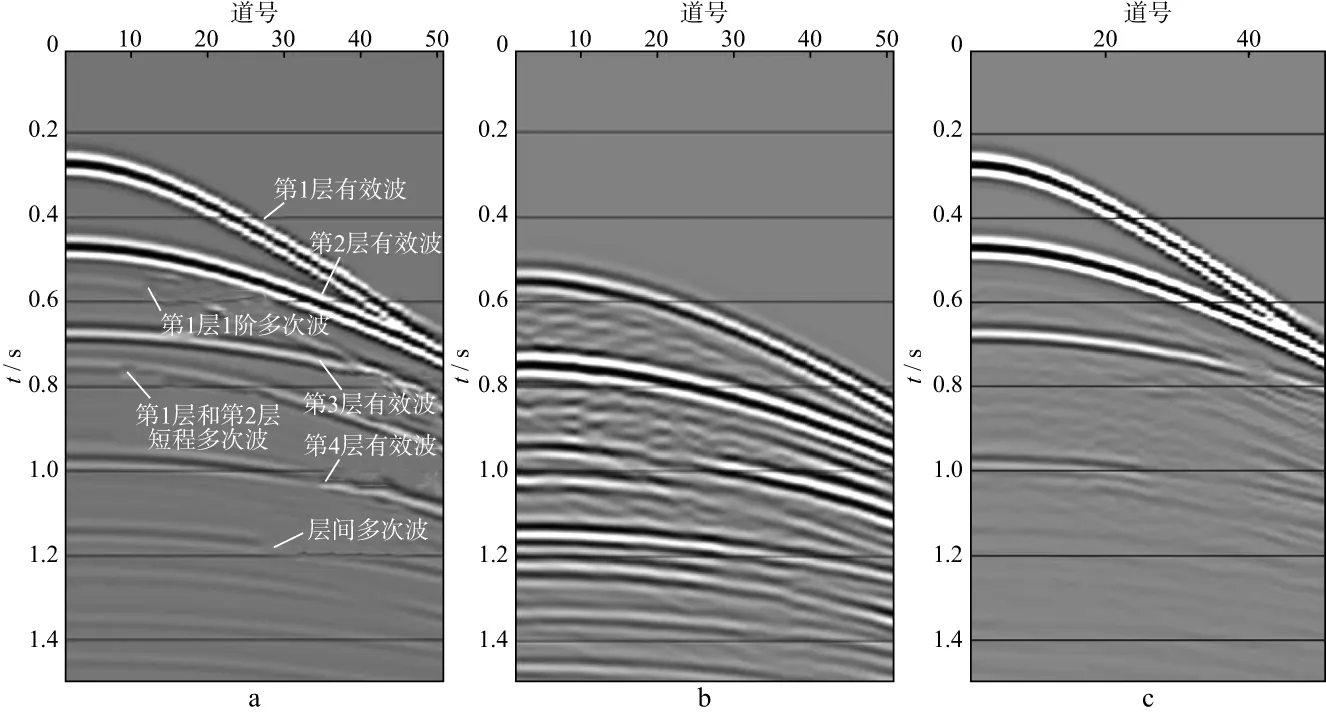
图6 单炮记录a 模拟的原始单炮记录(含多次波); b 采用波动方程方法预测的多次波; c 采用本文方法压制多次波后的单炮记录

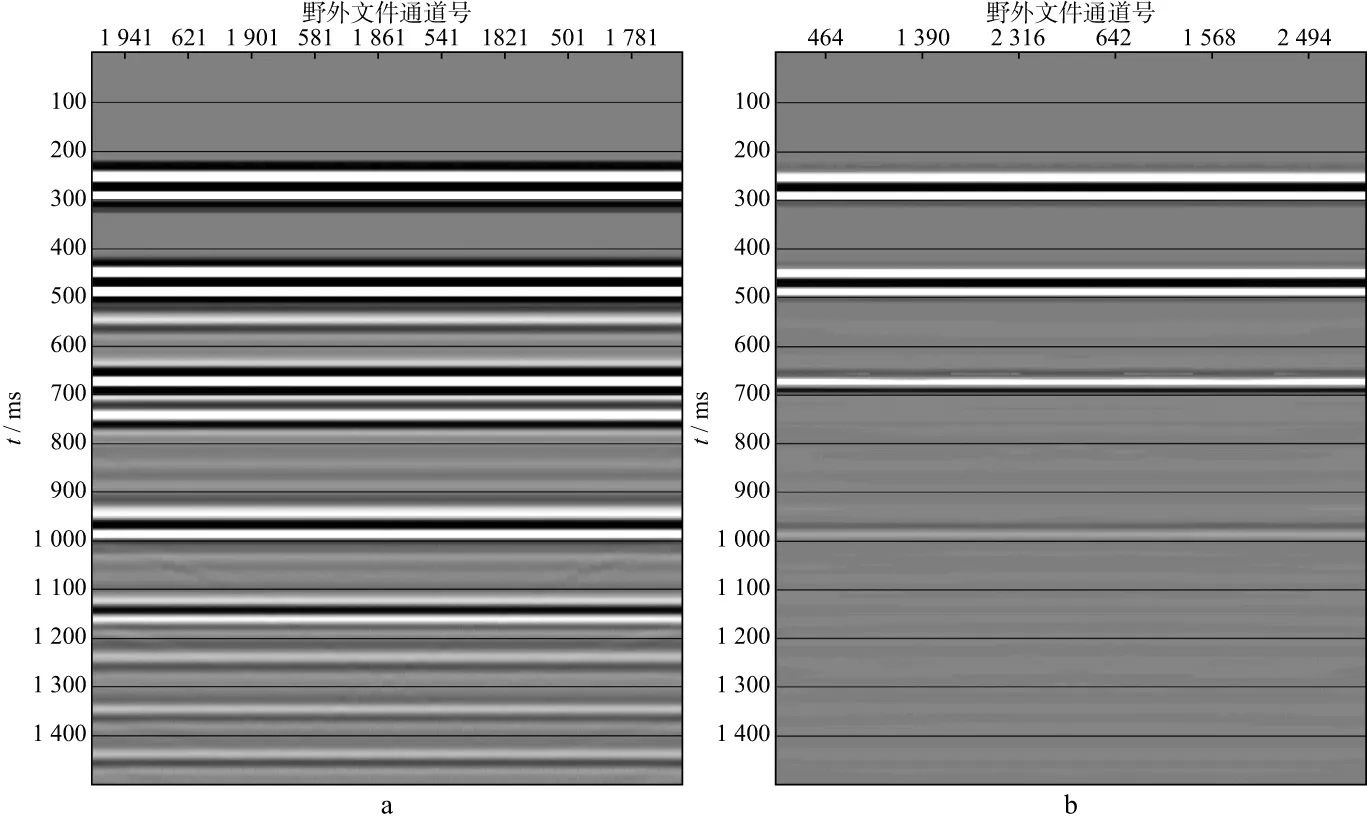
图7 原始数据剖面(a)与采用本文方法压制多次波后得到的零偏移距剖面(b)

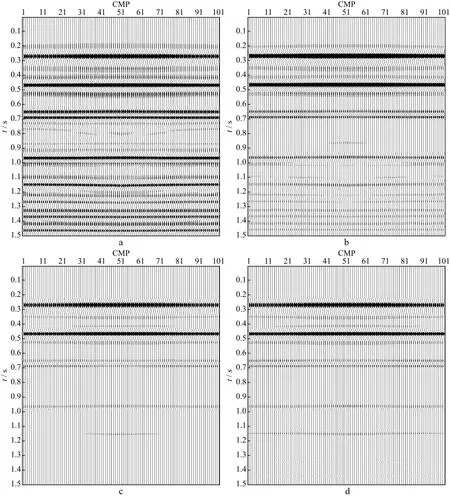
图8 原始数据剖面和不同方法压制多次波后的叠加剖面a 原始数据剖面; b L2范数方法; c L1范数方法; d 本文方法

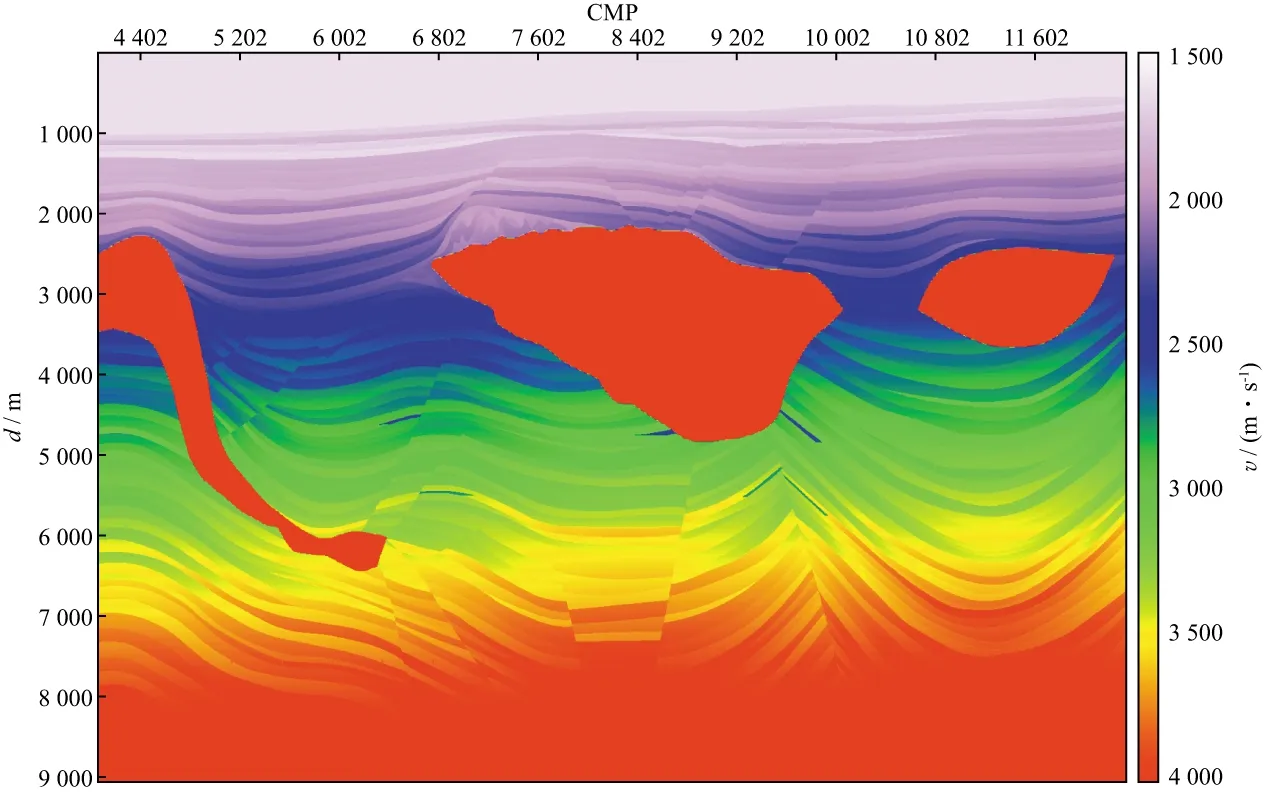
图9 SEG/EAGE Pluto速度模型

图10a为原始单炮记录,图10b为采用L2范数方法压制多次波后得到的单炮记录,图10c为采用L1范数方法压制多次波后得到的单炮记录,图10d为采用本文方法压制多次波后得到的单炮记录。对比可知,L2范数方法存在较多的多次波残留,L1范数方法噪声残留较少,而本文方法压制噪声的效果最好。从图11 的叠加剖面上也可看出,本文方法压制多次波的效果要优于L1范数和L2范数方法,海底多次波残留较少。

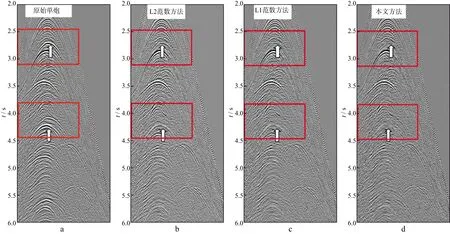
图10 原始单炮记录和不同方法压制多次波之后的单炮记录a 原始单炮记录; b L2范数方法; c L1范数方法; d 本文方法

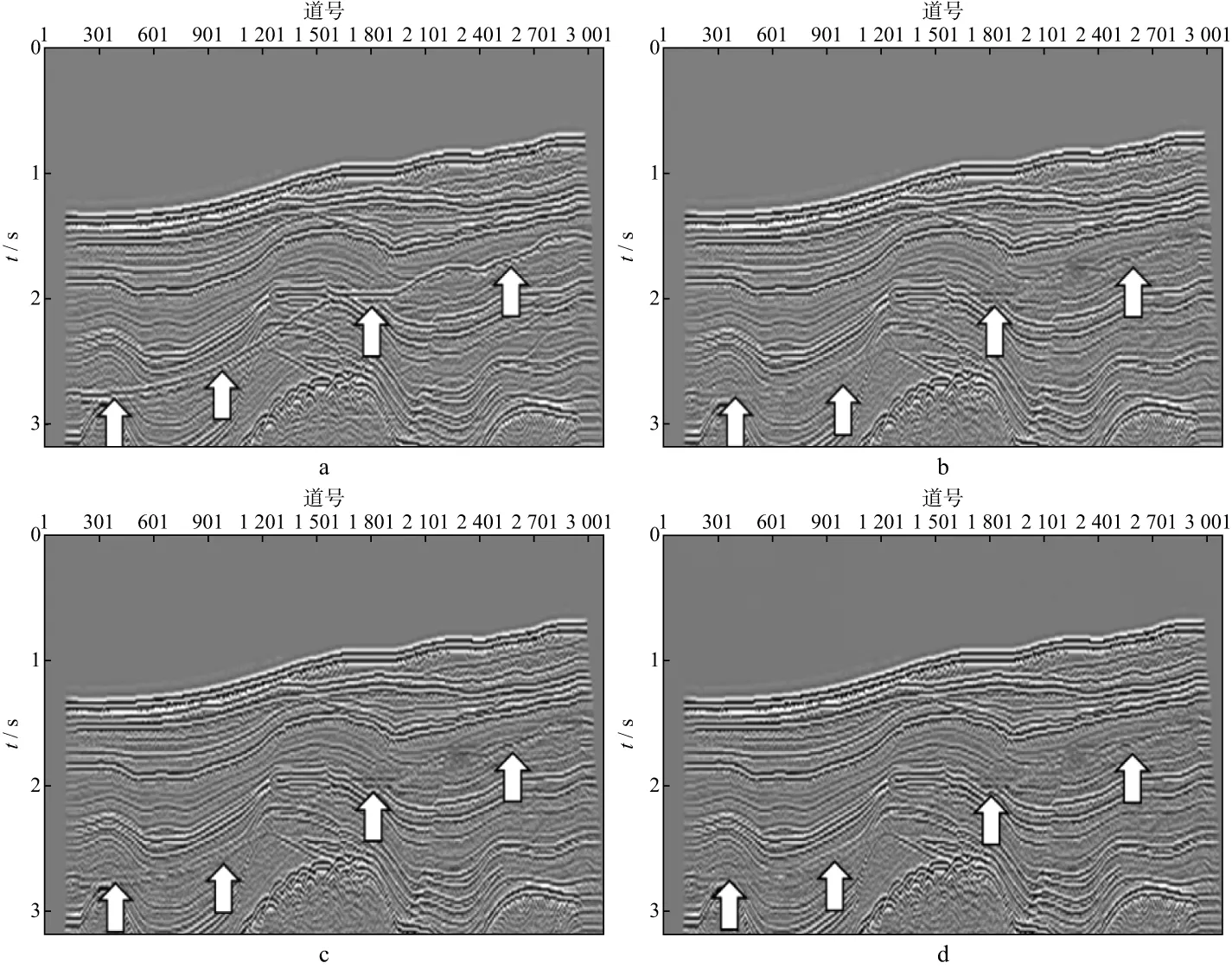
图11 不同方法压制多次波后的叠加剖面a 原始数据; b L2范数方法; c L1范数方法; d 本文方法

3 结束语

本文采用的自适应加权混合L1/L2范数匹配相减压制多次波方法兼顾了L1范数方法适合有效信号能量强、多次波能量弱的优点以及L2范数方法适合有效信号能量弱、多次波能量强的优点,并克服了L1范数和L2范数方法的缺点。模型测试结果表明,该方法可以有效地分离地震数据中的有效波与多次波,实现多次波的压制,具有独特的优势及良好的推广应用价值。