采摘机器人恒速抓取环境模拟及其控制器设计

钱志杰, 姬 伟, 陈光宇, 赵德安

(江苏大学电气信息工程学院, 江苏 镇江 212013)

苹果是我国优势农产品,年产量颇高．运用机器人采摘技术既能提高苹果的采摘效率, 也能缓解农业劳动力缺失的问题．然而, 现有的采摘机器人在抓取过程中极易造成果实损伤, 直接和间接损失率高达51%[1]; 因此, 研究机器人无损抓取技术以及提高末端执行器的柔顺性和稳定性具有重要的实用价值．王学林等[2]提出适合末端执行器双指抓取果实的接触力跟踪阻抗控制算法, 该算法将抓取果实的力和位置控制的关系等效为阻尼-刚度-惯量模型, 能更快、更稳地控制接触力度; Xu[3]提出一种在高速夹持情况下对力和位置柔顺调节的鲁棒阻抗控制方法. 但上述方法均未考虑未知的抓持环境, 限制了机器人柔顺控制算法在复杂环境中的应用．Li等[4]采用基于价值函数方法的阻抗学习技术, 通过反复调整外环阻抗控制器的参数, 在未知的动态环境中获得理想的阻抗模型; Duan等[5]提出一种新的自适应变阻抗力跟踪控制方法,能够跟踪动态期望力并补偿环境不确定性,显著减小了未知环境对控制器的影响: 但以上方法采用了基于环境反馈量的方式, 没有针对环境进行建模．为实现末端执行器的柔顺控制,针对阻抗控制性能受未知环境参数影响的问题[6], 本文提出模拟接触环境的方法, 以期解决上述问题,为改进采摘机器人的设计提供依据．

1 抓取环境模型及等效刚度

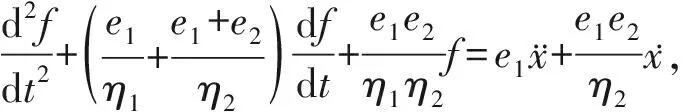
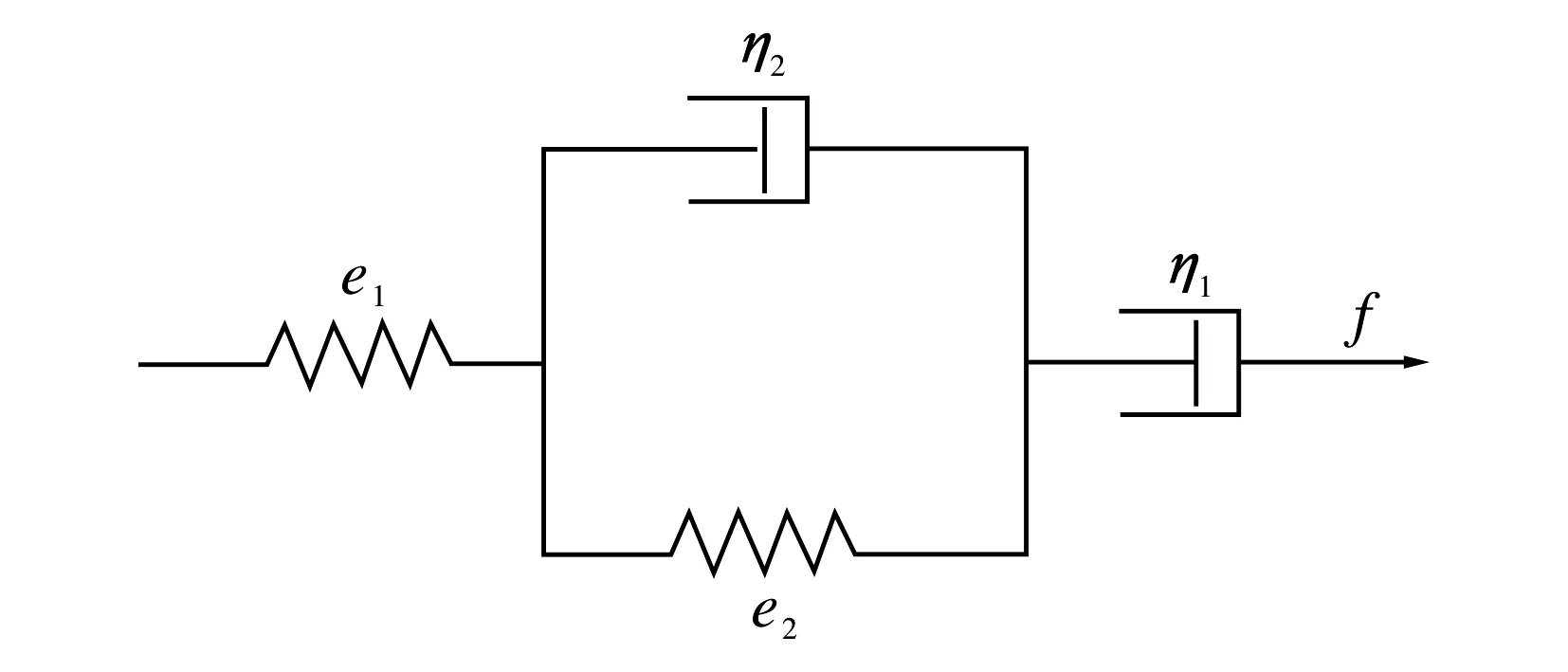
图1 四元件Burgers模型Fig.1 Four-element Burgers model

根据文献[8]的匀速夹持果实复合碰撞模型, 夹持过程包括以下3个阶段:

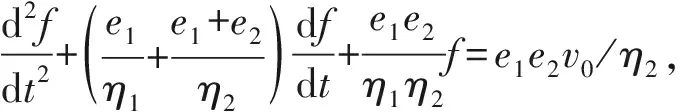
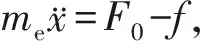
f=F0-C1eλ1t+eαt(C1cos (βt)+C2sin (βt)),

(1)

式中常数C1=-0.001 9,C2=21.78．

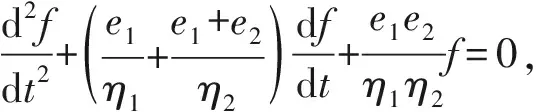
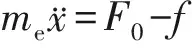
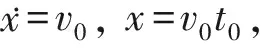
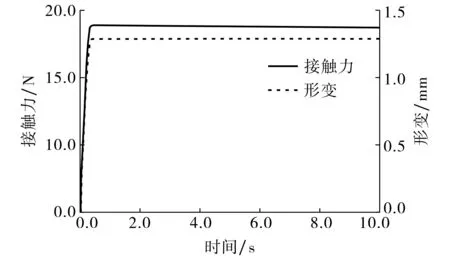
图2 匀速夹持下的接触力及果实形变曲线Fig.2 Contact force and fruit deformationcurves at uniform speed

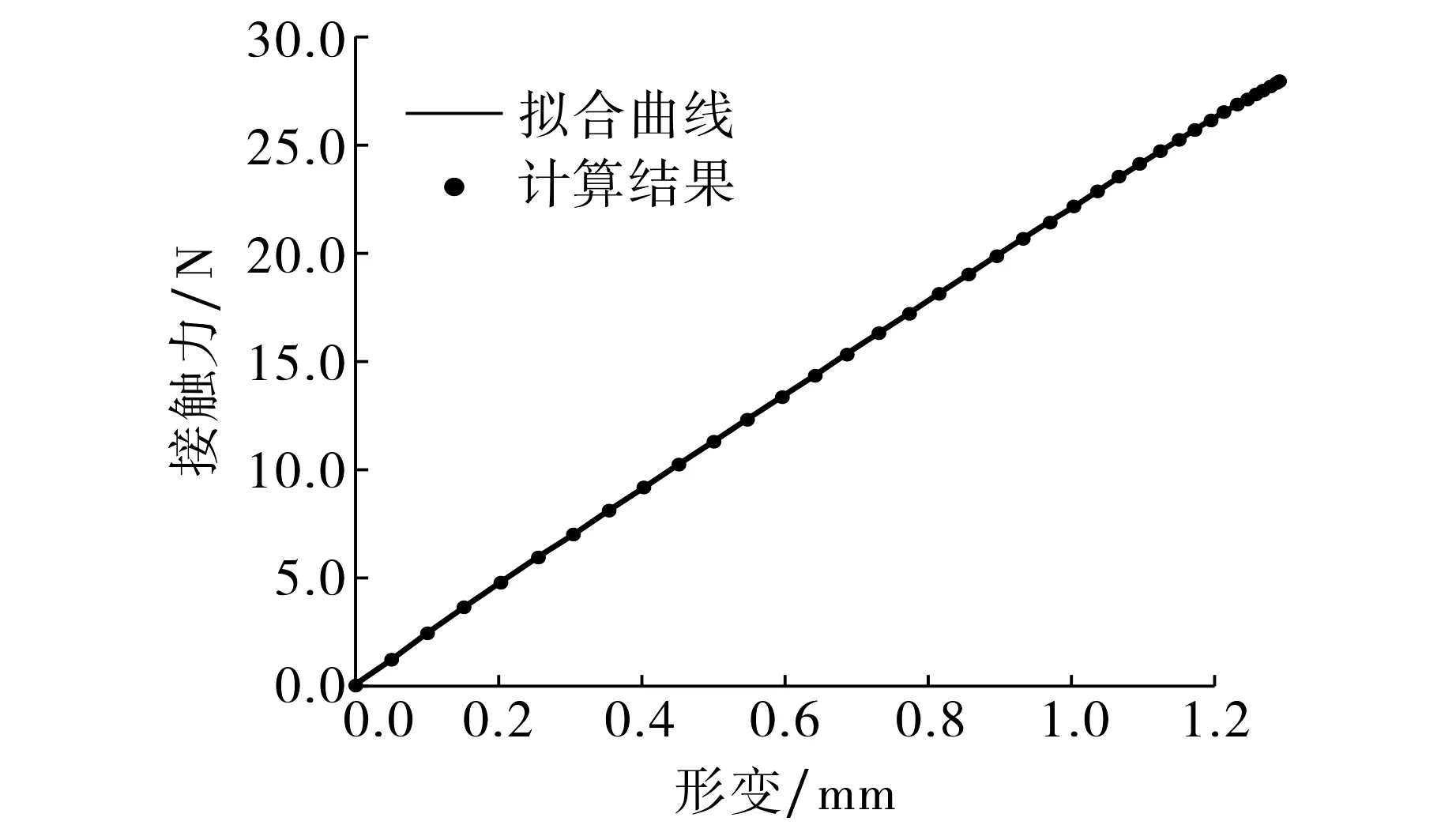
图3 果实形变与接触力关系的拟合曲线Fig.3 Fitting curve of fruit deformation-contact relationship force

2 末端执行器阻抗控制设计

2.1 抓持系统建模

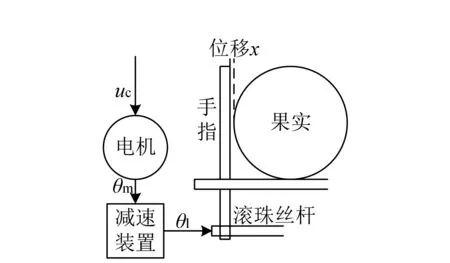
图4 驱动机构和末端执行器模型示意图Fig.4 Diagrammatic sketch of drivingmechanism and end-effector model

末端执行器抓持系统由驱动机构和双指结构末端执行器组成, 其模型示意图见图4．作为驱动机构的模型由减速装置和直流电机构成[10], 其中uc为控制电压, 电机转动角度θm通过减速装置得到负载转角θl, 再由滚珠丝杆转化为末端执行器手指的直线运动位移x．已知电机的转矩常数Kt=0.9, 齿轮减速比n=50, 反电势常数Kb=0.7, 惯量J=0.05 kg·m2, 黏滞摩擦系数D=0.38, 电枢电阻R=0.5 Ω, 功率放大系数Ks=50, 滚珠丝杆的导程为3.14 mm, 则末端执行器整体模型的传递函数为G(s)=x(s)/uc(s)=6/[s(s+8)], 其中s为复频域内的复数．

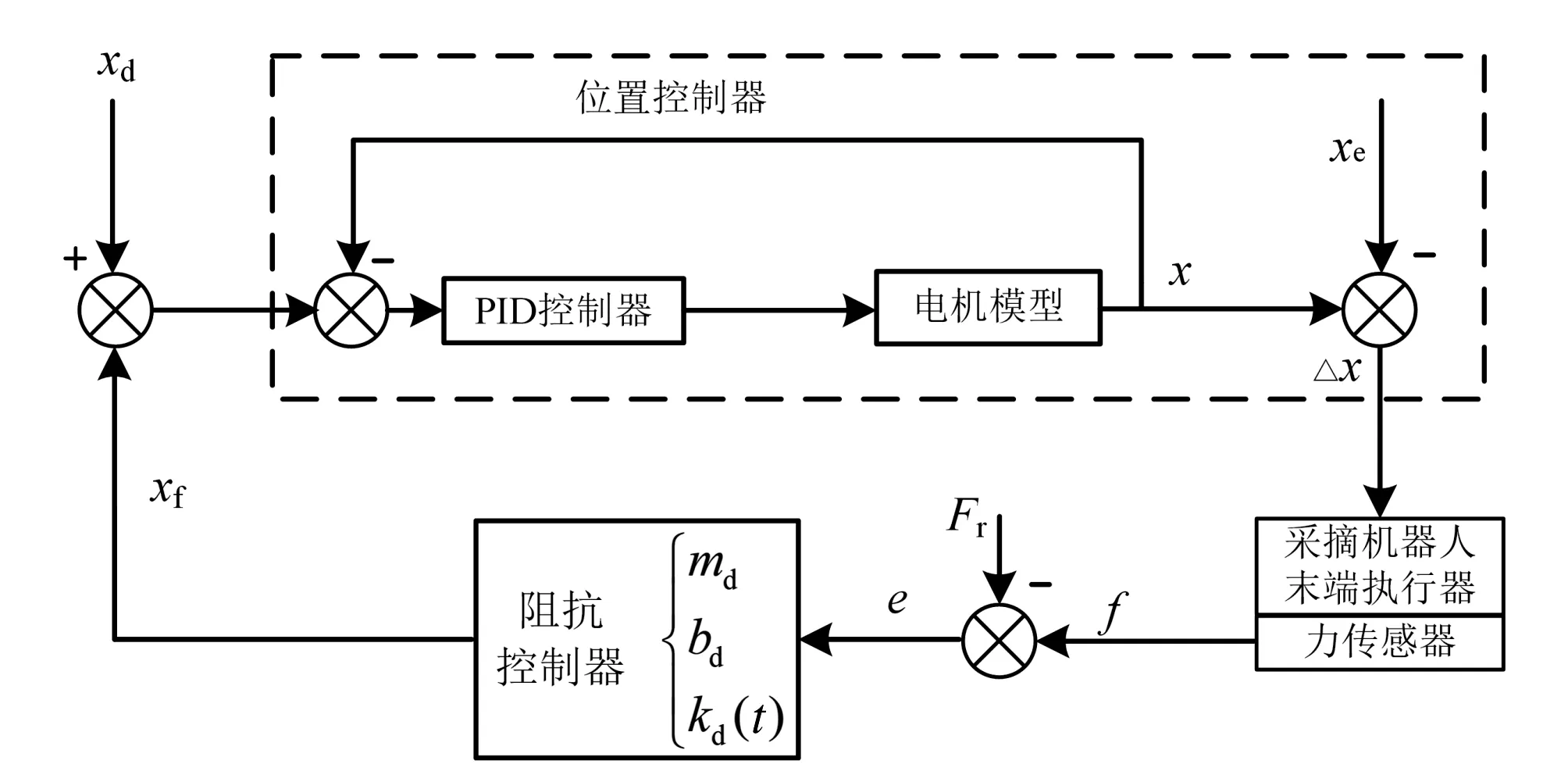
图5 末端执行器的阻抗控制策略示意图Fig.5 Impedance control strategy diagram of end-effector

2.2 阻抗控制策略

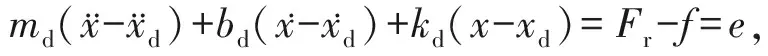
当机器人接触物体产生相互作用力时, 机器人末端与环境组成一个综合系统,此时可将果实的受力与形变的关系等效为一阶导纳模型, 即当末端执行器对果实施加作用力时只产生位移[5], 有f=ke(x-xe), 表明接触力与环境刚度、环境位置和实际位置有关, 而实际位置与位置偏移量和期望位置有关[13]．由于环境刚度未知, 通过期望位置xd求解接触力误差会较大, 所以本文采用环境模拟函数f(x)代替f求解接触力．

3 仿真结果与分析

设末端执行器阻抗控制系统的主要参数为惯性参数md=1 N·m-1, 阻尼参数bd=100 N·m-1, 刚度参数kd=500 N·m-1, 期望力fr=10 N, 仿真时间1 s, 采样时间为1 ms．采用Matlab对采摘机器人末端执行器的阻抗控制系统进行仿真, 得到如图6所示的接触力、期望力以及阻抗控制器输出的位置偏移量随时间的变化曲线．由图6可知, 接触力曲线超调量较小, 约为2.5%, 调节时间约为0.5 s, 控制系统能够满足实时性要求,外环阻抗控制器输出的位置偏移量最大值为10.32 mm,且在接触力稳定后输出为0．由于已知抓持系统的模拟环境函数, 通过位置控制器输出的实际位置与环境位置之差可求得果实的接触力, 故接触力的变化主要由实际位置的变化决定．为直观展现位置控制器输出的变化过程, 仿真得到实际位置变化率随实际位置和时间变化的关系如图7所示．由图7可知, 初始时位移变化率的增长速度很快, 0.05 s时达到最大值0.61 mm·s-1, 对应位移为0.24 mm, 之后位移变化率随位移增加而下降,直至位移到达峰值时位移变化率为0．此时由于实际位置略超过稳定值,于是开始反向调节, 最终趋于稳定(见局部放大图)．

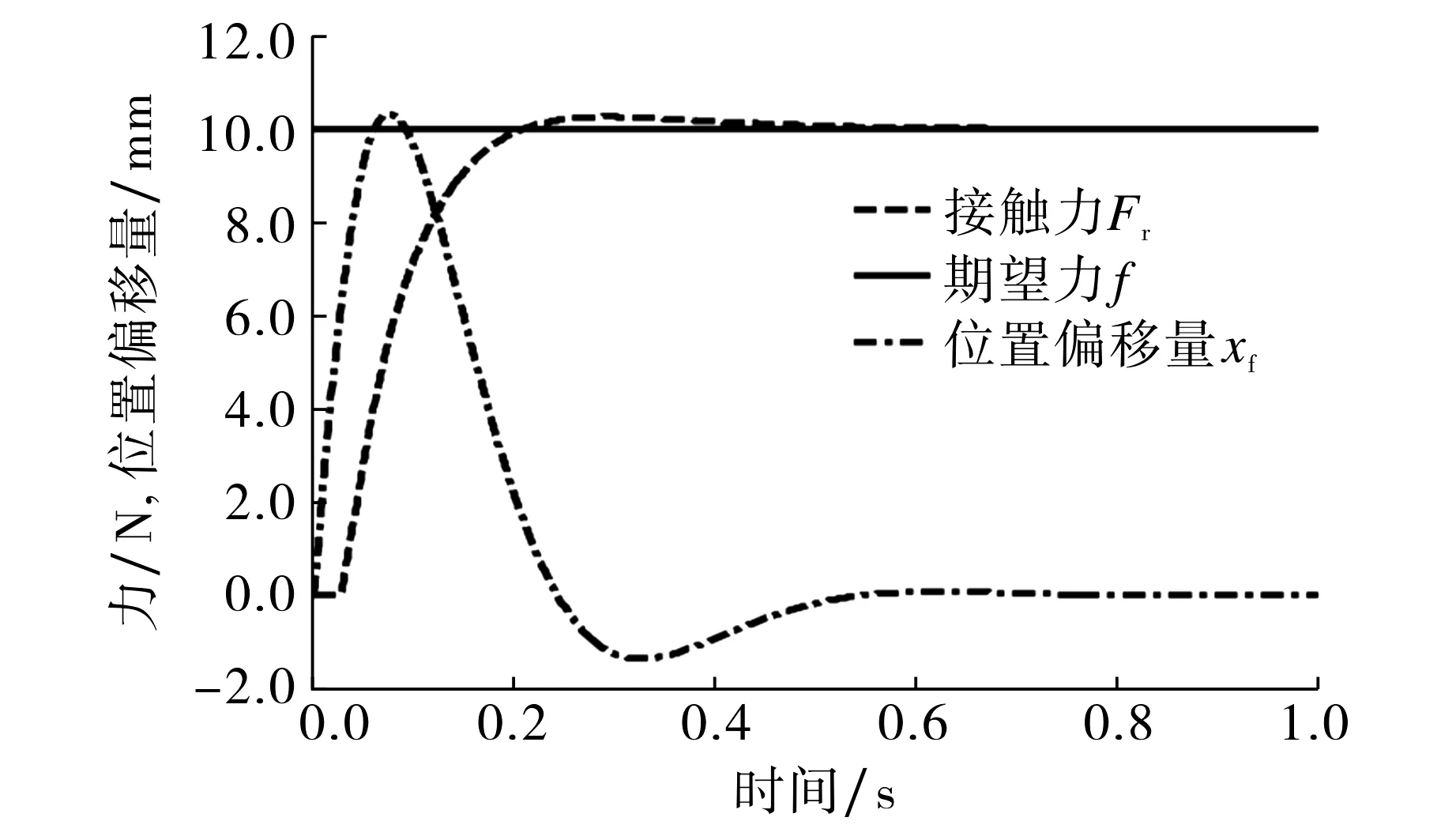
图6 接触力、期望力及控制器输出的位置偏移量随时间的变化曲线Fig.6 Curves of contact force, expected force and position offset output of controller with time

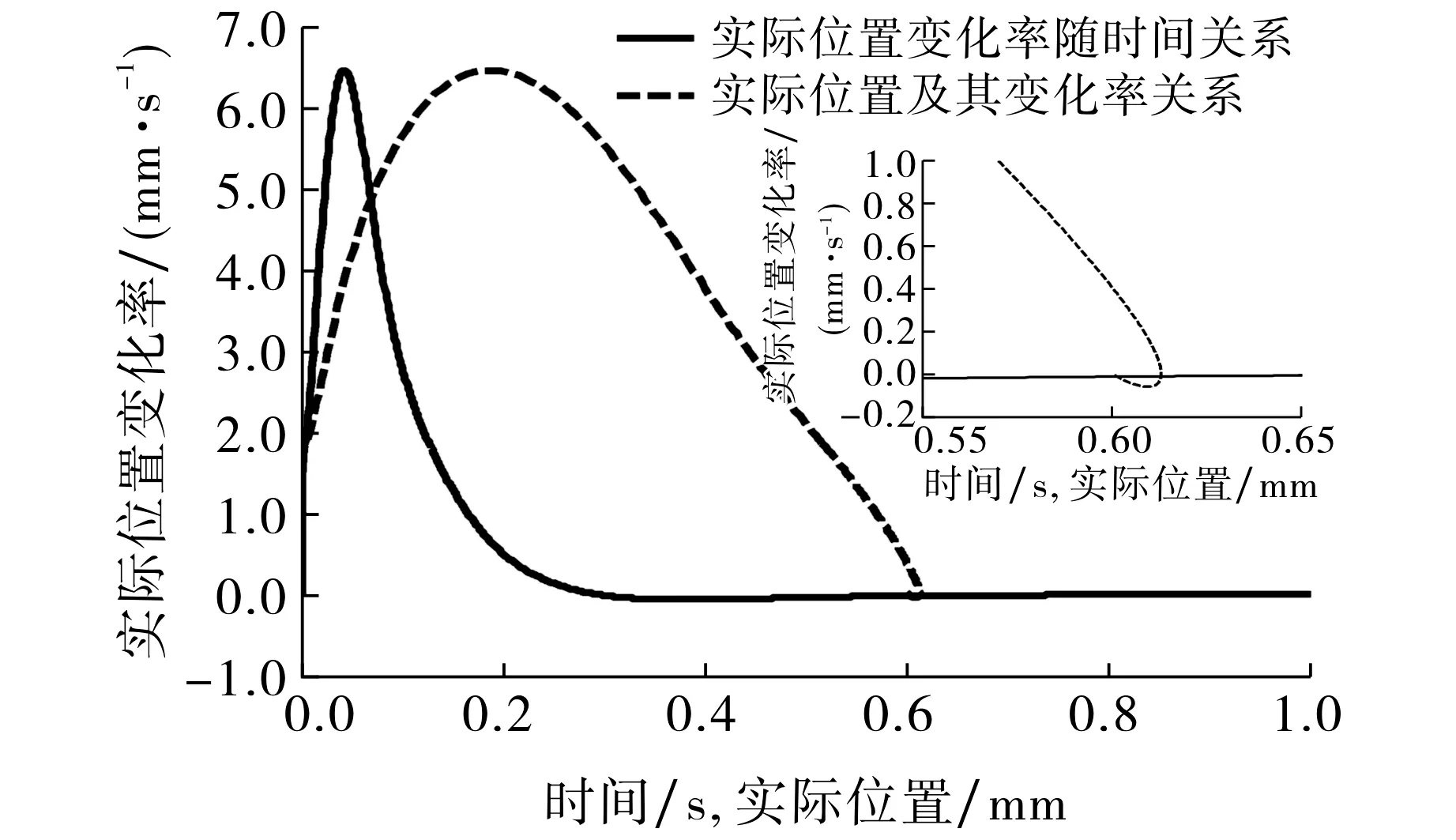
图7 实际位置变化率随实际位置以及时间变化的关系Fig.7 The relationship of real position change ratewith real position and time