交角不对中转子-轴承系统非线性动力学行为研究

李自刚　李明　江俊

摘要： 考虑转子交角不对中和质量不平衡等因素，研究了在滑动轴承支承下柔性转子-轴承耦合系统的非线性动力学行为。首先，基于转子间交角不对中的约束关系，利用第二类Lagrange方程推导了具有交角不對中故障的柔性多转子系统运动微分方程。采用数值方法，分析系统的非线性振动特性，例如，系统的轴心轨迹、响应频谱和最大Lyapunov 指数等。结果表明：在较低转速时，系统主要呈现出与转速同步的周期运动特性。随着转速的提高，稳态响应在某些参数下出现分叉、跳跃以及混沌等非线性现象。最后讨论了交角不对中量以及质量不平衡对系统动力学特性的影响。

关键词： 非线性动力学; 转子-轴承系统; 交角不对中; 分叉与混沌; 质量不平衡

中图分类号： O322; O347.6; TH113.1 文献标志码： A 文章编号： 1004-4523（2019）03-0509-08

DOI：10.16385/j.cnki.issn.1004-4523.2019.03.016

引 言

转子-轴承系统是旋转机械的核心组成部分。在实际系统中，由于加工精度、安装误差等原因，相邻转子的轴线往往存在不对中现象，即使对中良好的转子也会在其频繁启停过程中产生位置偏离。转子不对中能够引起机组的剧烈振动和异常响声，已成为机械故障最为重要的原因之一，如在大型发电机组中，不对中常常引起轴的挠曲变形、油膜失稳以及转子与定子间的碰磨等故障，危害很大[1-4]。文献[2]通过对实际机组的故障诊断，指出引起系统振动超标的根本原因是发电机-励磁机联轴器不对中。在文献[3-4]中，作者以实际发电机转子系统为研究对象，分别研究了具有平行不对中和轴承不对中故障的转子系统动力学行为，揭示了该类系统的一些非线性振动特征。然而，工程中往往也存在转子间的几何关系为交角不对中的故障形式。因此研究在滑动轴承支承下具有交角不对中约束的多转子-轴承耦合系统的非线性振动特性及其参数影响对系统的动力学设计、安装以及运行中的故障诊断具有重要意义。

关于交角不对中的研究最早可以追述到上个世纪70年代，但对此引起广泛关注的大约始于80，90年代。近10年来，随着国民经济和国防工业的快速发展，转子系统趋于大型、高速、重载，而转子与定子之间的间隙却在相对缩小，转子不对中所引起的振动也就变得更加严重，这要求转子系统的动力学设计更为精确合理。文献[5]利用有限元法分析了一个简化的不对中转子模型，并指出二倍频分量是这类转子系统的特征频率;文献[6]中，作者通过分析联轴节的变形和受力，研究了交角不对中轴系的扭振特征。文献[7-8]利用数值方法分别研究了由球铰联轴器和柔性联轴器连接的两个刚性转子系统的振动特性，并分析了角度不对中量和轴承刚度等因素对系统的动力学特性的影响，取得了一些重要的研究成果;文献[9]则采用Lagrange方法分析了2个支承在线性化滑动轴承上的刚性Jeffcott 转子系统的动力学特性，其中不对中效应主要体现在系统的弹性力上，而在系统的动态力中未予以考虑。近年来，一些学者则更加关注于振动信号中的谐波响应。文献[10]通过分析轴心轨迹和频谱图的特点，揭示了不对中转子系统的一些非线性动力学行为;文献[11-12]则考虑了2个转子间的连接刚度，建立了刚性多转子系统的动态不对中模型，研究表明当转角不对中时，系统的振动主要以工频为主，同时存在着组合频率成分;文献[13]从实验角度对双跨转子的不对中和不平衡耦合问题进行了试验研究。文献[14]采用随机理论分析了在非线性支承下刚性转子的角不对中问题。

以上关于交角不对中的研究中，所分析的机械结构大多表现为转子与轴承同时具有不对中，或允许较大角补偿的柔性联轴器-转子系统。例如，文献[15]建立了含万向铰偏斜旋转轴的横向振动模型，该结构允许较大的角不对中量。而对于轴承对中良好，但转子交角不对中的情况研究还比较少（轴承不对中便于调节，转子不对中则不便）。由于滑动轴承间隙限制和长度效应的影响，这种不对中情况不能允许转子间有过大的角位移，但其对整个系统稳定性产生的影响却是不能忽视的。本文考虑了质量不平衡等因素后，重点探讨了转子间具有交角不对中约束的柔性转子-轴承耦合系统非线性动力学行为。并深入分析了在不同转速下交角不对中量以及质量不平衡对系统动力学特性的影响，为该类转子的故障检测和在线监测提供理论依据。

1 具有交角不对中故障的转子-轴承系统动力学模型

1.1 转子系统动力学模型

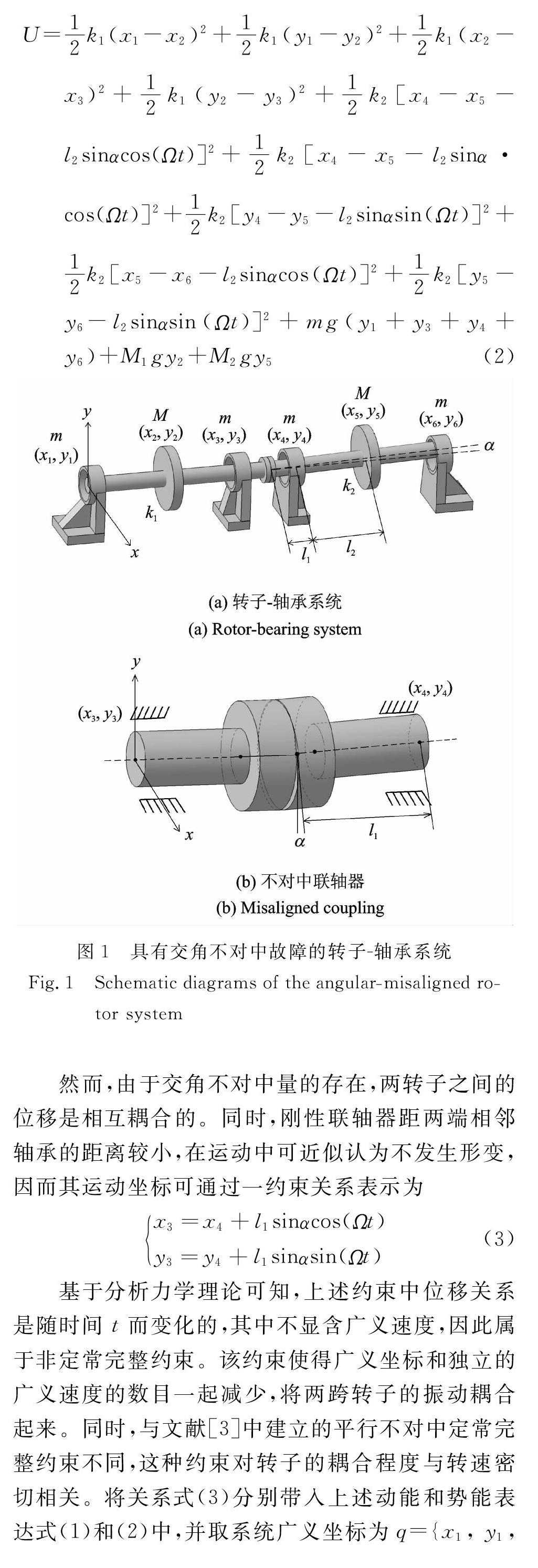
图1为具有交角不对中故障的转子-轴承系统示意图。其中两转子间通过刚性联轴器相连，并且在运动过程中保持大小不变的角不对中量α;m，M分别为轴颈和转子本体的集中质量;xi，yi为集中质量点在坐标系oxy下的坐标;k为转轴刚度;a为圆盘的质量偏心;Ω为转子的转速;t为时间。为方便问题的讨论，现作如下基本假设：（1） 转子间交角不对中量为微量;（2） 联轴器两端的相邻轴承之间距离相对较小，不发生形变;（3） 2圆盘在转轴的中间且近似地认为作平面涡动。

2.2 转速对交角不对中转子系统的影响

图3为采用4-5阶变步长Runge-Kutta法经过充分衰减后求得的转子系统在不对中轴承处的稳态响应随转速变化的分叉图。从图中能够看出，对于对中情况（α=0），系统响应在整个转速区间内始终保持周期运动。于此对比，微小不对中时（α=0.001 rad），系统在亚临界和超临界转速区间内呈现出一系列的分叉现象和混沌振荡。在无量纲转速ω≈2.45时系统通过倍周期分叉进入混沌运动状态，此时转子的横向振动幅值较大;随着转速的提高，在线性共振区附近系统的混沌运动消失并重新回到周期轨道;而在ω≈4.40时转子的稳态响应出现准周期分叉，其中，当ω≈4.80时，系统的振幅迅速增大，直至最后碰到轴承内圈。图4为其对应的最大Lyapunov指数曲线。由图4可见，转子响应分叉图与最大Lyapunov指数曲线图在周期运动、准周期运动和混沌运动的描述上一一对应，但在转子响应分叉图难以区分开的准周期运动和混沌运动，在最大Lyapunov指数曲线图上则可以清楚区分开。

图5为在不同转速时交角不对中对转子系统响应频率和轨迹的影响。由图可见，在图中的各转速下对中转子均以工频振动为主，呈现出周期运动特征，其轴心轨迹为一椭圆形，且幅值较小。对比来看，当不对中量α=0.001 rad时，在亚临界转速ω=2.0下其响应的Poincaré截面上呈现出1条封闭的曲线，表明系统在该转速下作准周期运动。从轨迹图上可见，系统的稳态响应在1个环域内作较为复杂的准周期振荡，频域上主要表现为工频及其倍频分量;另外在0.423倍工频等处有明显的离散谱峰，这是由于不对中导致滑动轴承的油膜压力分配改变，从而可能诱发油膜涡动[1]。当ω=2.5时，转子的轴心轨迹较为凌乱，频域内出现连续谱成分，Poincaré截面上呈现出无规则的点集，并且在该转速下最大Lyapunov指数为0.0060，表明系统已进入混沌运动。在临界转速附近ω=4.2时，转子系统的响应虽返回为周期1运动，但其轴心轨迹为明显的“月牙形”，且在某些位置曲率半径较大，频谱图中2倍频成分突出，这些正是交角不对中故障具有的典型特征[5，10]。并且此时最大Lyapunov指数为-0.0059。当转子处于超临界ω=4.7时，系统经历分叉再次进入非周期运动。频谱中相互不可公约的谐波分量出现，在该转速下系统响应的最大Lyapunov指数趋近于0，这些特征充分说明此时系统处于准周期状态。

2.3 不对中量对交角不对中转子系统的影响

图6为交角不对中转子稳态响应在不同转速下随不对中量变化的分叉图。从图中可以看出，在较低转速ω=2.0时，对于微小角不对中量，系统能够保持在周期1运动。但随着不对中量的逐渐增大，在α=0.0006 rad附近，转子的稳态响应开始出现准周期运动，其涡动轨迹明显增大。而在超临界转速ω=4.5下，随着不对中量的增大，系统的动力学行为表现的非常复杂，在α=0.0008 rad时直接从周期运动过渡到混沌振荡。

为了进一步研究不对中量对系统非线性振动特性的影响，分析了在不同交角不对中量时转子系统的稳态响应振幅随转速变化曲线。图7中当交角不对中量α=0时，即为对中情况下，系统的运动较为平稳，其振动幅度较小。然而不对中量的增大使转子的稳态响应趋于复杂，出现明显的跳跃现象。对比图3可以看出，这种幅值跳跃现象是由于交角不对中故障而引起的转子系统定性行为改变（解的数量变化）。而对于较大不对中量α=0.0010 rad时，随着转速的增加转子的振幅迅速增大，最终碰到轴承内圈。

2.4 质量偏心对转子系统动力学特性的影响

下面主要讨论质量偏心变化对系统响应的影响情况。图8（a）和（b）分别为当无量纲转速ω=2.00和ω=4.50时，交角不对中转子系统的稳态响应随质量偏心变化的分叉图。从图8（a）可以看出，随着质量偏心的增加，作用在转子上的不平衡激励增大，转子的稳态振动中出现明显的倍周期分叉现象。在不平衡量A≈0.10时，2倍周期中的每一个分支分别出现准周期分叉，形成“肺”状的两片孤立区域，此时转子的振动幅度较大。从图8（b）中可见，转子的质量不平衡能够引起系统的周期分叉，在A=0.125时其稳态响应经历短暂的准周期振荡后，出现周期6运动，这预示着系统的运动将变得非常复杂。

图9为在具有微小不对中量α=0.0005 rad时，不同质量偏心下轴颈中心横向振动的幅频特性曲线。经过对比能够看出，质量偏心是影响系统振动特性的重要因素。在低转速时，较大的偏心量能够使得转子稳态响应出现明显的幅值跳跃等非线性振动现象。然而值得注意的是，在较高转速时减小质量不平衡量使得靠近联轴器的轴承处振动状态并未改善，反而增大了转子的振动幅度。文献[18]中通过实际机组的测试数据同样反映了这种趋势。

3 结 论

考虑了质量不平衡等因素后，重点讨论了转子间具有交角不对中约束的柔性转子-轴承耦合系统非线性动力学行为。首先，根据描述交角不对中的约束关系，利用第二类Lagrange方程建立了具有交角不對中故障的柔性多转子系统动力学模型。理论分析表明，交角不对中转子系统是1个具有强非线性特征的10自由度非自治系统。采用数值方法重点分析了不对中转子系统的动力学行为，并深入讨论了在不同转速下交角不对中量和质量不平衡对系统动力学特性的影响，主要结论如下：

1）嵌入了非定常完整约束的转子系统使得两转子间的位移通过角不对中量相互耦合，其耦合程度与转子转速密切相关。同时由于油膜间隙和长度效应的影响，该约束影响轴颈内油膜压力重新分配，使得非线性油膜力与角不对中量α以及sin（Ωt）， cos（Ωt）相关，进而引起系统的复杂运动。

2）在较低转速时，系统主要呈现出与转速同步的周期运动特性。随着转速的提高，稳态响应在某些参数下出现分叉、跳跃以及混沌等非线性现象。

3）系统的径向振动出现明显的工频和倍频成分，并且在某些转速和不对中量下可能出现高次和低次谐波分量，轴心轨迹呈现“香蕉”型。

4）交角不对中能够引起系统失稳，使转子的横向振幅增大，因此在实际系统中， 应该严格控制转子间的角不对中量。

5）在一定转速下，随着质量偏心的增加，作用在转子上的不平衡激励增大，转子的稳态振动中出现明显的倍周期分叉以及振幅跳跃现象。

参考文献：

[1] Lu Siliang， He Qingbo， Wang Jun.A review of stochastic resonance in rotating machine fault detection[J]. Mechanical Systems and Signal Processing，2019，116：230-260.

[2] 郭玉杰，李 克，石 峰.某台汽轮发电机联轴器不对中振动故障的诊断处理[J].轴承，2013，8：56-58.

Guo Yujie，Li Ke，Shi Feng.Diagnosis and treatment for vibration fault of coupling misalignment on a turbine generator[J].Bearing，2013，8： 56-58.

[3] Li Zigang， Jiang Jun， Tian Zhui.Stochastic dynamics of a nonlinear misaligned rotor system subject to random fluid-induced forces[J].Journal of Computational and Nonlinear Dynamics，2017， 12： 011004.

[4] 李自刚，李 明.具有轴承不对中故障的柔性非圆截面多转子系统非线性动力学行为[J].振动工程学报，2012，25（1）：68-73.

Li Zigang，Li Ming.Nonlinear dynamics of flexible multi-rotor system with a misaligned journal bearing and non-circular cross section of shaft[J].Journal of Vibration Engineering，2012，25（1）：68-73.

[5] Felipe Wenzel， Katia Lucchesi Cavalca， Vibration signatures of a rotor-coupling-bearing system under angular misalignment[J].Mechanism and Machine Theory， 2019， 133： 559-583.

[6] 陈予恕， 李 军.汽轮发电机组轴系弯扭耦合振动问题研究综述 [J].汽轮机技术，2012，54（3）：161-164.

Chen Yushu，Li Jun.Research on bending-torsion coupling vibration of shaft system of turbine generator[J].Turbine Technology，2012，54（3）：161-164.

[7] Slim Bouaziz，Molka Attia Hili，Mohamed Mataar，et al.Dynamic behaviour of hydrodynamic journal bearings in presence of rotor spatial angular misalignment[J].Mechanism and Machine Theory，2009，44：1548-1559.

[8] Redmond I.Study of a misaligned flexibly coupled shaft system having nonlinear bearings and cyclic coupling stiffness—Theoretical model and analysis [J].Journal of Sound and Vibration，2010，329：700-720.

[9] Al-Hussain K M.Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment[J].Journal of Sound and Vibration，2003，266（2）：217-234.

[10] Palolo Pennacchi， Andrea Vania， Steven Chatterton. Nonlinear effects caused by coupling misalignment in rotors equipped with journal bearings[J].Mechanical Systems and Signal Processing， 2012，30：306-322.

[11] 李 明.轉角不对中故障的转子系统非线性动力学特征[J].振动、测试与诊断，2011，31（5）：552-556.

Li Ming.Nonlinear dynamics characteristics of rotor system with angular misalignment[J].Journal of Vibration， Measurement & Diagnosis，2011，31（5）：552-556.

[12] Li Ming.Nonlinear vibration of a multirotor system connected by a flexible coupling subjected to the holonomic constraint of dynamic angular misalignment [J].Mathematical Problems in Engineering，2012：243758.

[13] Wang Nanfei， Jiang Dongxiang.Vibration response characteristics of a dual-rotor with unbalance- misalignment coupling faults： theoretical analysis and experimental study[J].Mechanism and Machine Theory，2018，125： 207-219.

[14] Li Zigang，Jiang Jun，Tian Zhui.Nonlinear vibration of an angular-misaligned rotor system with uncertain parameters[J].Journal of Vibration and Control，2016，22（1）：129-144.

[15] 朱拥勇，王德石.含万向铰偏斜旋转轴的组合共振及其稳定性分析[J].应用力学学报，2012，29（4）：361-367.

Zhu Yongyong，Wang Deshi.The stability analysis on combination resonance of misaligned rotary shafts driven through a universal joint[J].Chinese Journal of Applied Mechanics，2012，29（4）：361-367.

[16] Farzad Hemmati， Mohammad Miraskari， Mohamed S Gadala.Dynamic analysis of short and long journal bearings in laminar and turbulent regimes， application in critical shaft stiffness determination[J]. Applied Mathematical Modelling， 2017，48：451-475.

[17] Pawe Pietkiewicz，Sawomir Banaszek，Grzegorz ywica.The stability loss of the rotor-slide bearings system under random load variations[J].Journal of Vibroengineering，2017，19（7）：4921-4935.

[18] 王延博.大型汽轮发电机组轴系不对中振动的研究[J].动力工程，2004，24：768-774.

Wang Yanbo. Shaft mis-alignment induced vibration in high capacity steam-turbine generator sets[J]. Power Engineering，2004，24：768-774.

Abstract： The non-linear dynamical behaviors caused by the faults of angular misalignment and mass unbalance of the journal bearing supported flexible rotor-bearing system are investigated in this paper. Firstly， the motion equation of the rotor system is derived by the second class Lagrange method with the effects of the motion relation between the two rotors， in which a rheonomic holonomic constraint characterized by the angular misalignment is embedded. Then its nonlinear vibration features， such as the frequency spectra， rotor orbit and Poincaré section， and the largest Lyapunov exponent under different conditions are primarily analyzed based on numerical techniques. The results reveal that the vibration of the rotor system are synchronous at low speed， while as the rotating speed increase， some non-linear characteristics such as jumping， period-doubling and chaotic motions will occur. Furthermore， the parameter analysis for the effects of angular misalignment and mass unbalance is also discussed.

Key words： nonlinear dynamics; rotor-bearing systems; angular misalignment; bifurcation and chaos; mass unbalance

作者簡介： 李自刚 （1986-），男，讲师。电话： （029）85583131; E-mail： lzghsfy@hotmail.com