T形截面振子的驰振特性试验研究

燕翔　练继建　刘昉　任泉超　张军　邵楠

摘要： T形振子的流致振动响应表现出了“非自限制”特性，随着流速的增大出现驰振现象，振动增强，有利于能量利用。但T形振子在复杂环境条件及自身截面变化条件下的研究尚未开展。基于此，进行了T形振子的试验研究，旨在探索其流致振动完整响应规律及在不同截面高宽比下的响应差异，具体结论如下：与三棱柱振子类似，T形振子也存在硬、软驰振现象，阻尼比较大时，出现硬驰振现象，而阻尼比较小时出现软驰振现象;软驰振响应中，振子的驰振具有自激发特性，由涡激振动激发而成;硬驰振响应中，振子需外力才可激发驰振;随着截面高宽比的增大，振动响应逐渐由硬驰振转化为软驰振，且驰振分支中振幅与频率均有所降低。

关键词： 流致振动; 涡激振动; T形截面; 驰振; 截面高宽比

中图分类号： TV131.2+9; P743.1  文献标志码： A  文章编号： 1004-4523（2019）03.0431.08

引 言

流致振动（Flow.Induced Motion，FIM）现象[1]广泛的存在于各类工程领域当中，对结构物具有较大的破坏能力[2.3]。近年来随着海洋能源、电子技术、流体力学及空气动力学的发展，学者们发现流致振动的巨大动能有非常可观的利用价值。随后，诸如VIVACE（Vortex Induced Vibration for Aquatic Clean Energy）[4]等一系列的流致振动发电设备相继提出，并逐步优化。所谓流致振动发电，即采用一些特殊的振动发电设备汲取流致振动的能量，从而将流体动能转化为可利用的电能或其他能量。在学术界，伴随流致振动研究及能量利用需求的不断增长，流致振动机理的研究快速稳步发展。

流致振动中最典型的两种振动形式为涡激振动（Vortex.Induced Vibration， VIV）与驰振（Galloping），上述两种振动的能量利用均有先例。VIV是由于流体黏性作用使得其在绕流柱体后侧产生了交替脱落的漩涡，从而引起了柱体横向的往复运动[1]，诱因主要源自漩涡脱落，最为典型的是圆柱绕流VIV现象;而驰振则是由于振动过程振子升力失稳原因造成的，其主要出現在非轴对称振子（如正三棱柱、正四棱柱等）的流致振动中。

基于发电目标下的涡激振动及驰振的研究近年来发展较为迅速，以密歇根大学Bernatisis团队的研究成果最为显著。借助于其开发的虚拟阻尼弹簧系统[5.6]（Virtual Damping.Spring （Vck） System）及被动湍流装置[7]（Passive Turbulence Control， PTC），密歇根大学开展了高阻尼[5]、高雷诺数[8]、变刚度[9.10]、变质量[9.10]等条件下的圆柱涡激振动特性及发电试验，发现高雷诺数、较高阻尼、低质量及加装PTC的圆柱振子有助于提高振动强度，并有利于电能的汲取，此外研究还发现PTC圆柱在特定的情况下还会出现驰振现象。值得注意的是，在Park等[11]在对PTC圆柱进行试验的过程中首次发现了两种不同的驰振模式：软驰振（Soft Galloping， SG）与硬驰振（Hard Galloping， HG）。软驰振由涡激振动激发，大流速下驰振可自行激发;硬驰振则不可由涡激振动激发，大流速下驰振需特定外力才能激发。进一步，Zhang等[12]在对三棱柱研究中也发现了软、硬驰振现象，并指明了两种硬驰振类型，I型硬驰振与II型硬驰振。随后，Lian等[13]的研究结果表明：三棱柱的流致振动响应中，涡激振动与驰振均存在，是否激发或是否抑制依赖于振动系统的阻尼、刚度、质量及振子的截面形式。随着系统参数的改变，软、硬驰振的变化是一个不断演化的过程，故软驰振、I型硬驰振与II型硬驰振实际上是统一的现象在不同参数下的不同表现。相对于圆柱振子、四棱柱振子、六棱柱，T形振子与三棱柱的驰振能量较高，但其很可能也存在软、硬驰振现象。因此，有必要针对T形截面振子的流致振动进行系统研究[14]，探究T形截面振子的驰振特性，以此指导流致振动振子设计。

但目前而言，T形截面振子的流致振动研究内容尚不系统，只进行了无干扰条件下的振动特性研究，并未开展在外界干扰下的流致振动特性研究以及振子截面形式改变条件下的驰振影响研究。为更好地了解T形截面振子的完整流致振动响应，探索其驰振特性，本文基于文献[14]的研究基础进行更为深入全面的试验研究，具体包括如下两个研究内容：（1）开展有外界干扰条件下流致振动试验，旨在探索T形截面振子的流致振动完整响应规律及驰振特性;（2）开展不同截面高宽比下T形截面振子的驰振对比研究，旨在揭示该振子的驰振影响因素，以此指导后续振子形式的优化与设计。

1 参数说明

为保证数据分析与规律阐述的准确性与统一性，文中所涉及到的有关参数及其相关说明、定义以及具体表达式如表1所示。

2 试验装置与物理模型

2.1 试验装置及测试设备  试验在自循环水槽中进行。水槽试验段宽度1 m，最大水深1.5 m，最大流速1.6 m/s，如图1所示。试验装置由固定支撑部和滑动体系两部分组成，具体的构件连接形式如图1（a）所示，其安装介绍见文献[14]。位移采用磁致位移传感器进行测量，其安装于固定支撑一侧，传感器量程0.800 mm，精度误差±0.05%。流速采用毕托管.压差计联合测试方法进行，精度误差±0.1%。上述传感器如图1（b）和（c）所示。

2.2 振子模型及参数

本文试验研究包括两项内容：（1）外界因素干扰下的T形截面振子的完整响应规律;（2）截面高宽比对T形截面振子流致振动响应规律的影响。

针对内容（1），本文采用与文献[14]相同的振子进行，即特征宽度D为0.1 m、长度L为0.9 m、厚度d为1 cm的有机玻璃T形振子。振子两端设置端板，以起到减小边界条件影响的作用[15]，端板厚度也为1 cm。此外，振子的振动参数也与文献[14]相同，即选取刚度条件为K=1200 N/m，以及4种不同的阻尼比ζ条件，分别为0.234，0.197，0.176，0.070。

針对内容（2），本文选取5种特征高度H的T形振子进行流致振动试验（如图2所示），特征高度H分别为0.15，0.12，0.1，0.9，0.8 m，其对应的截面高宽比α=H/D分别为1.5，1.2，1.0，0.9，0.8。为保证不同截面高宽比的响应研究具有可比性，所有振子的特征宽度D均为0.1 m，长度L均为0.9 m，且通过调整滑动体系质量的方式使各振子的振动质量mosc保持一致。

2.3 试验装置原理

试验装置原理（如图3所示）：T形截面振子限位于垂直水流方向，受到弹簧回复力与机械阻尼力;当水流经过T形振子后，对振子施加横向力带动振子横向振动;振子运动通过传动装置带动发电机转子旋转;转子旋转切割磁感线进而发电;输出的电能通过电阻进行耗能，转化为电阻的热量，电阻用于改变系统阻尼系数。

3 结果分析

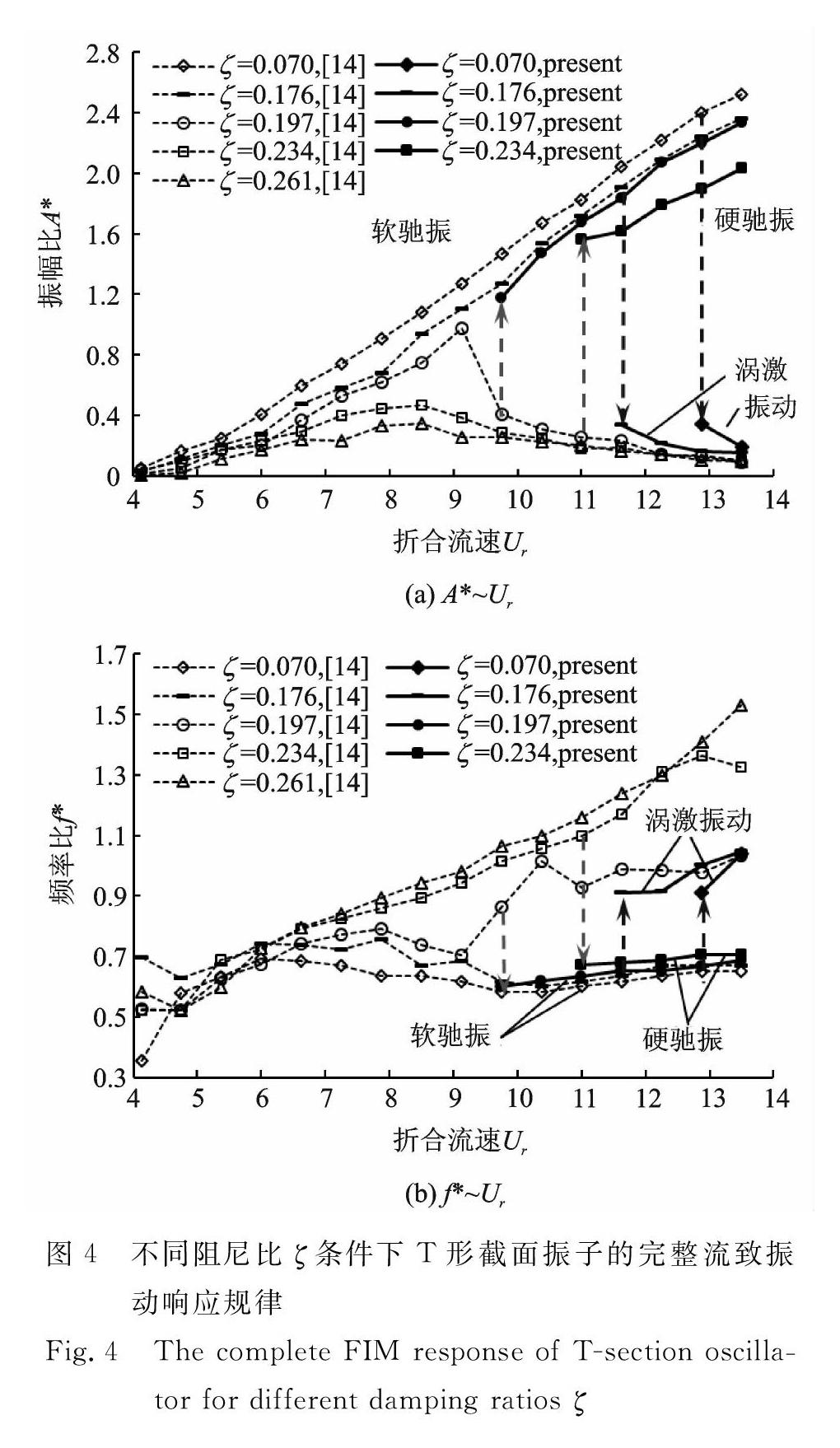
3.1 完整动力响应  本节重点考察T形截面振子的完整响应规律。为了保证试验结果对比的直观性，本文选择的T形截面的高宽比为1∶1，且选择与文献[14]相同的4组阻尼比条件进行试验，分别为：ζ=0.234，ζ=0.197，ζ=0.176，ζ=0.070。本文的试验过程考虑对振子施加外力扰动[13]。随流速增大，振子若无法自激励发展为驰振，则在大流速条件下对振子施加一个初始位移2D=20 cm;若振子可自激励发展为驰振，则在大流速条件下将振动的振子抑制然后观察其抑制之后的振动情况。基于该试验过程，得到如图4所示的完整振动响应结果。具体分析如下：

（1）ζ=0.234工况。若不存在外界干扰，振子的振动仅展现了典型的涡激振动响应规律，振幅比A*随折合流速Ur的增大呈现出先增大再减小的规律（即初始分支、上部分支及下部分支），频率比f*随折合流速Ur的增大则呈现出持续增大的趋势。但若存在一个较大的外界推力（采用文献[13]的试验手段，本试验初始位移为2D=20 cm），可进一步得到驰振分支。当折合流速Ur>11以后，较大推力会迫使振动由涡激振动下部分支跳跃到驰振分支，此时振幅比突然增大（A*>1.6）且随折合流速Ur持续升高，而频率比f*则突然降低至f*=0.7附近。显然，这一现象与文献[12]中三棱柱的现象基本一致，说明此时的振子表现出硬驰振现象。

（2）ζ=0.197工况。与工况ζ=0.234类似，若不存在外界干扰，则试验结果仅表现出典型的涡激振动响应规律，但最大振幅比A*显著大于ζ=0.234工况，达到了A*=0.9的水平。若存在一个推力，则可得到驰振的响应结果。当然，对于ζ=0.197工况，其外激励驰振分支的起振流速要低于ζ=0.234工况，为Ur=9.75。可见，阻尼比的降低有利于外激励硬驰振的发生。

（3）ζ=0.261工况。在测试流速范围内0     （4）ζ=0.176工况。由于阻尼比较小，若不存在外界干扰，振子的振动会由涡激振动逐渐发展为驰振。振幅比A*随折合流速Ur的增大呈现出持续增大的规律（即初始分支、上部分支、涡激振动.驰振转变分支及驰振分支），频率比f*则随折合流速Ur的增大表现出先增大再降低最后维持在0.7附近（伴随有微弱的增长趋势）的规律。但若存在一个较大的外界抑制力（采用文献[13]的试验手段，本试验将位移降低）可进一步得到涡激振动下部分支。当折合流速Ur> 11.625后，较大抑制力会迫使振动由驰振转化为涡激振动，对应的振幅比A*降低到0.4以下，而频率比f*则升高到0.9以上。可见，此时的振动进入涡激振动的下部分支。由此说明，此时的振动实际为软驰振响应规律。

（5）ζ=0.070工况。与工况ζ=0.176类似，该工况下的振子表现出软驰振的响应规律：若不存在外界干扰，振子的振动会由涡激振动逐渐发展为驰振;若存在较大外力抑制，则振动则会由驰振转变为涡激振动，进入涡激振动下部分支。不过，由于阻尼比的进一步减小，可抑制发展为涡激振动的流速较工况ζ=0.176的有所升高，说明阻尼比的降低有利于自激励软驰振的发生。

综上，可得到T形截面振子的流致振动完整响应规律的特点如下：（1）随着阻尼比的降低，振动由硬驰振逐渐转变为软驰振;（2）随着阻尼比的降低，软驰振的自激励能力与硬驰振外激励能力都在逐渐增强;（3）软驰振存在涡激振动下部分支，而硬驰振需外界推力诱发形成。需要说明的是，上述T形截面的试验结果与已有的三棱柱结果较为相似。实际工程（包括振动控制与振动发电工程）中，应对该类型截面振子的软、硬驰振现象进行系统分析与预测，以保证有效的安全评估与能量评估。

3.2 时程与频谱特性

为了进一步探究T形截面的驰振激发特性，本节重点分析了不同驰振现象的激励模式。图5和6分别展示了软驰振与硬驰振在激励过程中的典型时程与频谱规律。其中，图5为折合流速降低到Ur=11.625时振子的振动响应，对应的阻尼比工况为ζ=0.176（较小阻尼比）;而图6则为折合流速在Ur=11时振子的振动响应，对应的阻尼比工况为ζ=0.234（较大阻尼比）。具体特性可归纳如下：

（1）对于ζ=0.176工况。振动信号在0.5 s时，振幅较小且不稳定，主频为在1 Hz附近，且不存在其他倍频特性，频谱带宽较大，振动能量不集中，说明此时振动处于VIV下部分支，振动诱发于漩涡脱落，且受到一定的抑制。振动信号进入5 s后，振动振幅随时间推移有明显增大趋势。当进入10 s后，振幅增到较高水平，且基本维持稳定，对应的频率响应呈现峰值明显的窄带频谱特征，主频在0.6 Hz左右，且存在2倍倍频与3倍倍频特征，说明此时振动处于驰振分支，振动诱发于升力失稳效应，单个振动周期内有多组漩涡脱落，振动强度较大。由此可见，在较小阻尼比条件下，流速的降低会使得T形截面振子由涡激振动（下部分支）自激励诱发成为驰振。

（2）对于ζ=0.234工况。振动信号在0.10 s时，振幅较小，振动不稳定，振动主频在0.9 Hz左右，频带较宽，能量较为分散，且未有任何振幅增大的趋势。说明振动处于VIV下部分支，诱发于漩涡脱落，且受到抑制。当信号进入10.12 s时，存在一个外界推力，此时振幅被迫增大到20 cm左右。随后，外力撤销，振子突然转变为大振幅、低频率的振动状态，振动频率在0.6 Hz左右，且频带较窄，能量集中，且存在微弱的2倍倍频与3倍倍频特征，说明此时振动处于驰振分支。由此可见，在阻尼比较大的条件下，T形截面振子不能由涡激振动自激励诱发成为驰振，但可通过外界激励的方式诱发驰振。因此，阻尼比较大时振动多呈现为完整的涡激振动响应。

3.3 截面高宽比的影响

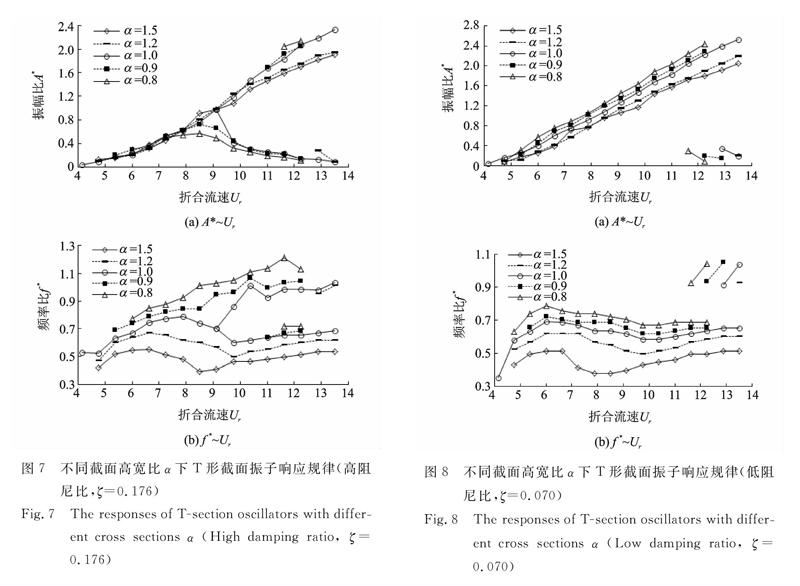
对T形截面而言，截面的高宽比显著影响振子的漩涡脱落特点与所受的横向力大小[16]。为此，本节重点讨论5组不同截面高宽比条件下T形截面振子的振动特性，高寬比分别为α=0.8，α=0.9，α=1.0，α=1.2及α=1.5。此外，为了对比结果更具普适性，本节选取了高、低两种阻尼比工况，分别为ζ=0.197与ζ=0.070。具体的试验结果如图7与8所示。

（1）高阻尼比工况，即ζ=0.197

驰振特性：当截面高宽比处于0.8≤α≤1.0时，振子表现为硬驰振现象，即需由外界激励才能迫使振动进入驰振状态，且随着高宽比的升高，驰振的起振流速在不断降低（Ur从11.625降低至9.75）;当截面高宽比处于1.2≤α≤1.5时，振子表现为软驰振现象，即无需外界激励，振子即可随流速增大而进入驰振状态，但当流速足够大时，外界抑制力会迫使振动再次进入涡激振动状态。由此可知，截面高宽比的增大有利于振动模式由硬驰振向软驰振发展。

振幅与频率：当振动处于涡激振动初始分支（即折合流速Ur<7.25）与下部分支（即折合流速Ur>9.75）时，各高宽比下的振幅差异并不显著;当振动处于涡激振动上部分支或涡激振动.驰振转变分支时（即折合流速7.259），高宽比越大，振幅反而越小。由此可见，截面高宽比的增大有利于涡激振动上部分支振幅的增大，从而迫使振子诱发了自激励的软驰振现象。这也就进一步解释了前述内容中高宽比对振动模式的影响规律。不论流速处于何种条件，也不论振动处于何种模式下，随着高宽比的增大振动频率是在不断减小的。此外，能够明显地看到随着高宽比的增大，软驰振的诱发流速是在不断降低的。由此，也进一步说明了截面高宽比的增大有利于驰振的发生这一基本规律。

（2）低阻尼比工况，即ζ=0.070

根据图8振幅比A*与频率比f*随折合流速Ur的变化规律可见，振动几乎在Ur=6.7就已进入了驰振状态（而对于ζ=0.176工况下的振子，均在Ur=8以后才进入驰振状态）。由于阻尼比较低，所有T形截面振子均表现为软驰振现象。另外，振子的振幅随截面高宽比的增大基本都表现为降低的趋势。

综上所述，随着截面高宽比的增大，振动响应逐渐由硬驰振转化为软驰振，且驰振分支中振幅与频率均有所降低。需要说明的是，振动振幅与频率的降低势必影响流致振动发电设备对于驰振能量的利用效果[17]。因此，需选择合理的截面高宽比，既保证振动特性良好，也保证其具有较高电能输出。

4 结 论

本文基于文献[14]的结果进行了进一步的T形截面振子流致振动试验研究，考察了不同外界条件下T形截面振子的涡激振动与驰振完整响应规律，探究了该类振子驰振发生可能性，并分析了振子截面高宽比对T形截面驰振发生规律的影响。本文旨在揭示T形截面振子的流致振动完整响应，为流致振动发电装置的振子设计提供参考。现得到结论如下：

（1）揭示了T形截面振子的流致振动完整响应规律：与三棱柱振子类似，T形振子也存在硬、软驰振现象;阻尼比较大时，振子表现为硬驰振现象，驰振分支需有外界推力且流速较大才能出现;阻尼比较小时，振子表现为软驰振现象，即涡激振动会自激励形成驰振，但若在较大流速下有外力抑制，振动会由驰振转为涡激振动，且振动受到抑制;随着阻尼比的降低，振子的驰振发生能力增强。

（2）指明了截面高宽比对T形截面振子驰振特性的影响：随着截面高宽比的增大，振动响应逐渐由硬驰振转化为软驰振，且驰振分支中振幅与频率均有所降低。

参考文献：

[1] 白莱文斯. 流体诱发振动[M]. 吴恕三， 译. 北京： 机械工业出版社， 1981.

Blenvins R D. Flow.Induced Vibration[M]. Wu Shusan， Trans. Beijing： China Machine Press， 1981.

[2] 黄 坤， 冯 奇. 梁索耦合结构的风致涡激振动[J]. 振动工程学报， 2011， 24（2）： 139.145.

Huang Kun， Feng Qi. The vortex.excited vibrations of coupled structure of cable.stayed beam[J]. Journal of Vibration Engineering， 2011， 24（2）： 139.145.

[3] 秦 浩， 廖海黎， 李明水. 大跨度变截面连续钢箱梁桥涡激振动线性分析法[J]. 振动工程学报， 2015， 28（6）： 966.971.

Qin Hao， Liao Haili， Li Mingshui. A linear theory of vortex.induced vibration of long span continuous steel box girder bridge with variable cross.section[J]. Journal of Vibration Engineering， 2015， 28（6）： 966.971.

[4] Bernitsas M M， Raghavan K， Ben.Simon Y， et al. VIVACE （Vortex Induced Vibration Aquatic Clean Energy）： A new concept in generation of clean and renewable energy from fluid flow[J]. Journal of Offshore Mechanics and Arctic Engineering， 2008， 130（4）： 041101.

[5] Lee J H， Bernitsas M M. High.damping， high.Reynolds VIV tests for energy harnessing using the VIVACE converter[J]. Ocean Engineering， 2011， 38（16）： 1697.1712.

[6] Sun H， Kim E S， Bernitsas M P， et al. Virtual spring.damping system for flow.induced motion experiments[J]. Journal of Offshore Mechanics and Arctic Engineering， 2015， 137（6）： 061801.

[7] Chang C C J， Kumar R A， Bernitsas M M. VIV and galloping of single circular cylinder with surface roughness at 3.0×104≤Re≤1.2×105[J]. Ocean Engineering， 2011， 38（16）： 1713.1732.

[8] Bernitsas M M， Ben.Simon Y， Raghavan K， et al. The VIVACE converter： Model tests at high damping and Reynolds number around 105[J]. Journal of Offshore Mechanics and Arctic Engineering， 2009， 131（1）： 011102.

[9] Sun H， Kim E S， Nowakowski G， et al. Effect of mass.ratio， damping， and stiffness on optimal hydrokinetic energy conversion of a single， rough cylinder in flow induced motions[J]. Renewable Energy， 2016， 99： 936.959.

[10] Ma C， Sun H， Nowakowski G， et al. Nonlinear piecewise restoring force in hydrokinetic power conversion using flow induced motions of single cylinder[J]. Ocean Engineering， 2016， 128： 1.12.

[11] Park H， Kumar R A， Bernitsas M M. Enhancement of flow.induced motion of rigid circular cylinder on springs by localized surface roughness at 3.0×104≤Re≤1.2×105[J]. Ocean Engineering， 2013， 72：403.415.

[12] Zhang J， Xu G， Liu F， et al. Experimental investigation on the flow induced vibration of an equilateral triangle prism in water[J]. Applied Ocean Research， 2016， 61： 92.100.

[13] Lian J， Yan X， Liu F， et al. Experimental investigation on soft galloping and hard galloping of triangular prisms[J]. Applied Sciences， 2017， 7（2）： 198.

[14] 練继建， 任泉超， 刘 昉， 等. T 形截面振子的流致振动特性试验研究[J]. 实验力学， 2017，32（2）： 216.222.

Lian Jijian， Ren Quanchao， Liu Fang， et al. Experimental study of flow.induced vibration characteristics of T.shape cross.section oscillator[J]. Journal of Experimental Mechanics， 2017，32（2）：216.222.

[15] Morse T L， Govardhan R N， Williamson C H K. The effect of end conditions on the vortex.induced vibration of cylinders[J]. Journal of Fluids and Structures， 2008， 24（8）： 1227.1239.

[16] Shao N， Lian J， Xu G， et al， Experimental investigation of flow.induced motion and energy conversion of a T.Section prism[J]. Energies， 2018， 11（8）： 2035.

[17] Lian J， Yan X， Liu F， et al. Analysis on flow induced motion of cylinders with different cross sections and the potential capacity of energy transference from the flow[J]. Shock and Vibration， 2017， 2017：1.19.

Abstract： The T.section prism will present the trend of unlimited amplitude response， which， to be exact， will undergo the galloping vibration as the velocity increases. This characteristic will benefit the energy harvest from the flow.induced motion （FIM）. Until now， few studies focused on the galloping characteristics of T.section prisms under complicated conditions and different cross section factors. To this end， a series of experiments are conducted to investigate the complete responses of the T.section prism and the influence of the cross section factor （height/width ratio）. The main findings are listed as follows： two types of galloping， i.e. the soft galloping （SG） and hard galloping （HG）， are found for the T.section prism. This feature has already been found in the triangular prism. When the damping is high， the prism presents the HG behavior， otherwise it presents the SG behavior. In the SG response， the galloping is self.excited by vortex induced vibration （VIV）. In the HG response， the galloping must be excited by external forces. As the cross section factor increases， the oscillation is transformed from HG to SG， and the amplitudes and frequencies will both decrease.

Key words： flow.induced vibration; vortex.induced vibration; T.section; galloping; cross section factor

作者簡介： 燕 翔 （1988.），男，助理研究员。电话：13752290971; E.mail：xiangyan@tju.edu.cnZ ··y^