动态子结构高效集成的主动力和界面力处理方法

邹明松　吴有生　孙建刚　

摘要： 在现有的船舶水弹性子结构分离与集成方法中，主船体结构的振动采用以模态广义坐标为变量的动力学方程进行描述，船内子结构的振动采用以空间物理位移为变量的动力学方程进行描述。通过两者的边界连接条件进行综合集成时，会遇到模态空间与物理空间的转换集成问题。针对该问题，提出了“虚拟模态”方法，一方面可以使动态子结构集成计算精确，另一方面可大幅减少子结构集成的计算量。理论上，该“虚拟模态”方法适用于其他领域类似的动态子结构集成计算问题。最后，通过数值算例，对该“虚拟模态”方法的正确性和适用性进行了验证。

关键词： 结构振动; 动态子结构方法; 流固耦合; 船舶振动

中图分类号： O327; U661.44  文献标志码： A  文章编号： 1004-4523（2019）03.0439.05

DOI：10.16385/j.cnki.issn.10044523.2019.03.008

引 言

动态子结构方法将复杂结构分解成一些较简单的子结构，根据子结构动态特性的计算或试验结果综合出整个复杂结构的动态特性。该方法已有较广泛而深入的研究与应用[13]。动态子结构方法可以基本分成两类，一类是模态综合法（包括固定界面模态综合法、自由界面模态综合法等），一类是界面位移综合法（包括界面位移直接综合法、聚缩阻抗矩阵综合超单元方法等）。其中第一类方法以模态坐标为待求量实现子结构之间的综合集成，第二类方法以空间物理位移为待求量实现子结构之间的综合集成。为提高动态子结构方法的综合精度与计算效率以及扩展其应用范围，国内外开展了大量的研究，提出了多种在基本方法基础上的改进方法[47]。

随着计算机水平的提升，动态子结构方法已应用于实船流固动力学分析中[8]。也有众多学者在流固耦合动态子结构方法的基础上，提出了多种新的思想。文献[9]将一个复杂的结构分解成主体结构和子结构两部分，考虑主体结构与流体介质的耦合作用，对于刚度、质量分布不确定的子结构采用概率统计的方法处理成模糊子结构（fuzzy structure）。文献[1011]提出将结构分解成高分辨率的局部子结构和低分辨率的主体结构，建立不同网格尺度的有限元模型或者解析模型进行独立求解和集成。文献[12]在声介质中三维结构水弹性力学理论（即船舶三维声弹性理论）[1314]的基础上，提出了专门用于解决船舶等复杂海洋浮体结构声弹耦合问题的水弹性子结构分离及集成方法。该方法将船舶结构分解成主船体和内部子结构两部分，采用水弹性方法实现主船体与水介质的流固耦合求解，通过边界连接条件完成主船体与子结构的综合集成。该方法可避免因部分子结构的修改导致整个流固耦合模型重新计算的问题，且在建模方面也只要修改子结构本身，不牵涉主船体模型。因此，特别适用于处理船舶内部子结构（如横舱壁、铺板、基座等）振动噪声传递效果分析与优化的问题。

经典的水弹性力学分析方法中[1516]，选用具有正交完备性的干模态（结构在真空中的模态）作为广义基函数进行求解，具有物理概念清晰、易于求解和便于后续计算结果分析的优点。该方法在船舶流固耦合领域具有广泛的应用。同样，在船舶水弹性子结构分离及集成方法中，主船体结构的振动也采用以干模态广义坐标为变量的动力学方程进行描述。当船内子结构的振动采用以空间物理位移为变量的动力学方程进行描述，利用边界连接条件进行综合集成时，会遇到模态空间与物理空间的转换集成问题。文献[12]中的方法是直接将主船体与子结构连接部位的力平衡条件代入相应的矩阵方程中，最终形成可显示求解的矩阵方程维数较大;整个计算复杂度和计算规模均存在一定的优化空间。针对该问题，本文提出了“虚拟模态”方法，其实质是将主船體结构上的主动力和界面力定义为广义坐标。该方法在实现主船体结构与内部子结构严格耦合的同时，使得最终形成的可显示求解的矩阵方程维数近似等于主船体结构与内部子结构之间的连接自由度数，从而使整个求解规模相对较小，计算效率大为提高。

1 基本方程推导

如图1所示结构，由主体结构和内部子结构两部分组成。不失一般性，采用该模型论述“虚拟模态”方法的具体内容。

1.1 主体结构的动力学方程

基于模态叠加方法，可得频域内以干模态主坐标为未知量的主体结构广义动力学方程-ω2MA+iωCA+KAq=DTAFA1

多数情况下，式（17）所示的矩阵维数近似等于主体结构与内部子结构之间的连接自由度数，因此整个求解规模相对较小。

多个内部子结构与主体结构集成耦合的操作过程与此类同。

2 算例验证

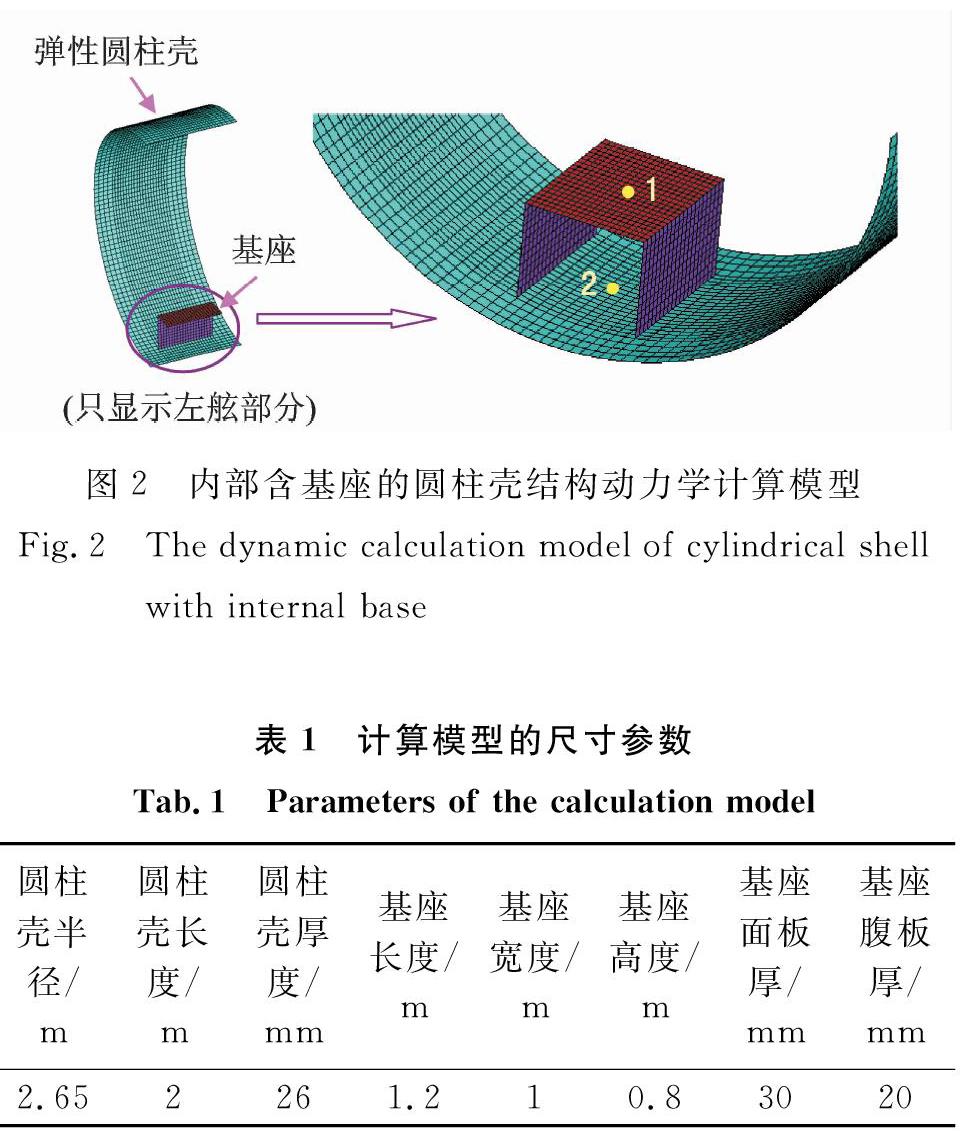
采用图2所示的内部含基座（内部子结构）的弹性圆柱壳（主体结构）计算模型（图2中左侧部分只显示了该模型的左舷一半），验证上节中所述的基于“虚拟模态”方法的子结构动态集成的计算精度。模型位于空气中，圆柱壳的两端为简支边界条件，整个结构的密度为7800 kg/m3，杨氏模量为2.1×1011 N/m2，泊松比为0.3，阻尼损耗因子为0.02，具体尺寸参数如表1所示。

在模型中的1号点上作用单位垂向简谐激励力，计算1号点和2号点的垂向振动速度响应。1号点位于基座面板的中部，2号点位于1号点正下方的圆柱壳中部。通过两个方法进行计算，一种是建立整个结构的有限元模型，采用直接法进行谐响应求解;另一种是采用上述基于“虚拟模态”的动态子结构方法进行谐响应求解。计算对比结果如图3所示。由图3可见，直接计算结果与动态子结构计算结果几乎完全重合，说明本文提出的“虚拟模态”子结构集成计算方法是正确的并具有较高的计算精度。

3 结 论

本文提出了一种“虚拟模态”方法，实现了以模态主坐标为待求量的主体结构与以空间位移为待求量的内部子结构之间的高效率和高精度的动态集成。该方法可应用于现有的水弹性子结构分离与集成计算，同时也适用于其他领域类似的动态子结构集成计算问题。通过一个内部含基座的弹性圆柱壳结构振动传递的数值算例，验证了该动态子结构集成的“虚拟模态”方法的正确性和适用性。

參考文献：

[1] 王文亮， 杜作润. 结构振动与动态子结构方法[M]. 上海： 复旦大学出版社， 1985.

Wang Wenliang， Du Zuorun. Structure Vibration and Dynamic Substructure Analysis Method[M]. Shanghai： Fudan University Press， 1985.

[2] 殷学纲， 陈 淮， 蹇开林. 结构振动分析的子结构方法[M]. 北京： 中国铁道出版社， 1991.

Yin Xuegang， Chen Huai， Jian Kailin. Substructure Method for Structure Vibration Analysis[M]. Beijing： China Railway Publishing House， 1991.

[3] 向树红， 邱吉宝， 王大钧. 模态分析与动态子结构方法新进展[J]. 力学进展， 2004， 34（3）： 289303.

Xiang Shuhong， Qiu Jibao， Wang Dajun. The resent progresses on modal analysis and dynamic substructure methods[J]. Advances in Mechanics， 2004， 34（3）： 289303.

[4] Suarez L E， Singh M P. Improved fixed interface method for model synthesis[J]. AIAA Journal， 1992， 30（12）： 29522958.

[5] 骞朋波， 尹晓春， 沈煜年， 等. 碰撞激发弹塑性波传播的动态子结构方法[J]. 力学学报， 2012， 44（1）： 184188.

Qian Pengbo， Yin Xiaochun， Shen Yunian， et al. Dynamic substructure method for propagation of elasticplastic wave induced by impact[J]. Chinese Journal of Theoretical and Applied Mechanics， 2012， 44（1）： 184188.

[6] 诸 赟， 张美艳， 唐国安. 一种基于子结构界面动刚度的模态综合法[J]. 振动工程学报， 2015， 28（3）： 345351.

Zhu Yun， Zhang Meiyan， Tang Guoan. A modal synthesis method based upon dynamic stiffness on interface[J]. Journal of Vibration Engineering， 2015， 28（3）： 345351.

[7] 白 斌， 白广忱， 费成巍， 等. 改进的混合界面子结构模态综合法在失谐叶盘结构动态特性分析中的应用[J]. 机械工程学报， 2015， 51（9）： 7381.

Bai Bin， Bai Guangchen， Fei Chengwei， et al. Application of improved hybrid interface substructural component modal synthesis method in dynamic characteristics analysis of mistuned bladed disk assemblies[J]. Journal of Mechanical Engineering， 2015， 51（9）： 7381.

[8] 邹春平， 陈端石， 华宏星. 船舶结构振动模态综合法[J]. 上海交通大学学报， 2003， 37（8）： 12131218.

Zou Chunping， Chen Duanshi， Hua Hongxing. Modal synthesis method of structural vibration analysis of ship[J]. Journal of Shanghai Jiaotong University， 2003， 37（8）： 12131218.

[9] Soize C. A model and numerical method in medium frequency range for vibroacoustic predictions using the theory of structural fuzzy[J]. J. Acoust. Soc. Am.， 1993， 94（2）： 849865.

[10] Franzoni L P， Park C D. An illustration of analytical/numerical matching with finiteelement analysis for structure vibration problems[J]. J. Acoust. Soc. Am.， 2000， 108（6）： 28562864.

[11] Park C D. Analyticalnumerical matching for fluidloaded structures with discontinuities[J]. J. Acoust. Soc. Am.， 2004， 116（5）： 29562968.

[12] 邹明松， 吴有生. 水弹性子结构分离及集成方法[J]. 船舶力学， 2014， 18（5）： 574580.

Zou Mingsong， Wu Yousheng. A method used for separating and coupling substructure based on hydroelasticity theory and dynamic substructural theory[J]. Journal of Ship Mechanics， 2014， 18（5）： 574580.

[13] 邹明松， 吴有生， 沈顺根， 等. 考虑航速及自由液面影响的声介质中三维结构水弹性力学研究[J]. 船舶力学， 2010， 14（11）： 13041311.

Zou Mingsong， Wu Yousheng， Shen Shungen， et al. Threedimensional hydroelasticity with forward speed and free surface in acoustic medium[J]. Journal of Ship Mechanics， 2010， 14（11）： 13041311.

[14] 邹明松. 船舶三维声弹性理论[D]. 无锡： 中国船舶科学研究中心， 2014.

Zou Mingsong. Threedimensional sonoelasticity of ships[D]. Wuxi： China Ship Scientific Research Center， 2014.

[15] Wu Y S. Hydroelasticity of floating bodies[D]. London： Brunel University， 1984.

[16] Bishop R E D， Price W G， Wu Y S. A general linear hydroelasticity theory of floating structures moving in a seaway[J]. Philosophical Transactions of the Royal Society of London A， 1986， 316（1538）： 375426.

[17] 恽伟君， 段根宝， 胡仲根. 模态综合超单元法及其在船舶动态计算中的应用[J]. 上海力学， 1982， （4）：818.

Abstract： In the hydroelastic substructure separation and integration method， the structural vibration of the main hull is described by dynamic equations in terms of the generalized modal coordinates， while the vibration of the internal substructure is expressed with dynamic equations in terms of the geometric coordinates of displacements. When carrying out a synthesis analysis in the light of the boundary connection conditions， there exist compatibility problems between the modal space and the geometric space. In order to deal with this problem， a virtual modal method is proposed in this work. This method will greatly reduce the computational effort for structural integration， with the calculation precision guaranteed at the same time. Theoretically speaking， this virtual modal method is also applicable to problem analogous in some other research areas. Finally， the correctness and applicability of this method are validated through a numerical example.

Key words： structural vibration; dynamic substructure method; fluidstructure interaction; ship vibration

作者簡介： 邹明松（1982），男，研究员。电话：（0510）85557312;Email：zoumings@126.comZ ··y^