曲径变通途——避开分类讨论，另寻简捷方法

一、运用最值思想，避免分类讨论

例1.奇函数 f(x)是R上的减函数，若对任意的 x∈(0，1]，不等式f(kx)+f(-x2+x-2)＞0恒成立，求实数k的取值范围。

解：∵f(kx)+f(-x2+x-2)＞0，且 f(x)是R上的奇函数，减函数，

∴f(kx)＞f(x2-x+2)

得到kx＜x2-x+2 (1)

故当 x∈(0，1]时，

显然有h(x)min=h(1)=3，∴k＜3-1，即k＜2

∴k的取值范围为(-∞，2)

点评：按照常规思路，由(1)式转化为x2-(k+1)x+2＞0在x∈(0，1]上恒成立问题，可令g(x)=x2-(k+1)x+2，然后根据二次函数性质及对称轴位置的变化，进行分类讨论，得到：

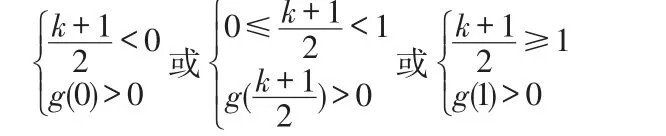
解得k＜-1或-1≤k＜1或1≤k＜2，从而求得k的取值范围为(-∞，2)。这样解就显得比较烦琐，因为有些不等式在区间上的“恒成立”问题，一般通过分离变量，转化为函数的最值问题求解。就可以避免分类讨论，使得解题过程简明快捷，少走弯路。

二、妙用换底公式，避免分类讨论

例2.设 0＜x＜1，a＞0且 a≠1，比较 |loga(1-x)|与|loga(1+x)|的大小。

分析：本例通常应分a＞1与0＜a＜1两种情况讨论，但运用换底公式消去a，就可避免分类讨论，从而达到简化解题过程的目的。

解：运用作商比较法，

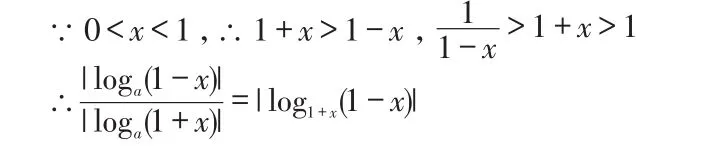
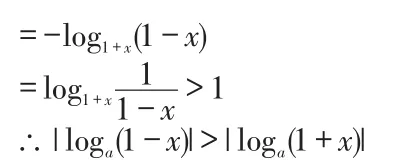
三、变更主元法，避免分类讨论

例3.设不等式mx2-2x-m+1＜0对于满足|m|≤2的一切m的值都成立，求x的取值范围。

分析：本例为含参数的不等式，关键是对参数的处理，从表面上看，是一个关于x的一元二次不等式，实质上是一个关于m的一元一次不等式，并且已知它的解集为[-2，2]，求参数的范围。因此通过参数m与未知数x的地位的变化，借助于一次函数图象，避免了繁杂的对参数的讨论。

解：设 f(m)=(x2-1)m+(1-2x)，它是以m为自变量的一次函数，其图象为直线，由题意知，这条直线当x∈[-2，2]时，线段在y轴的下方，满足它的为

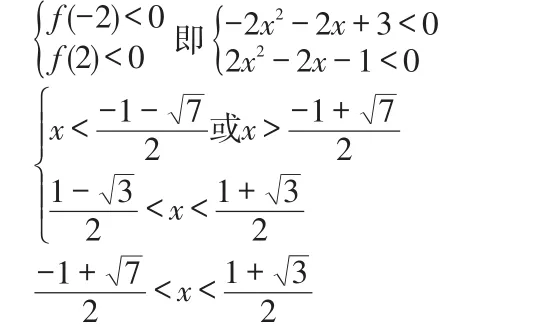
四、借助函数性质，避免分类讨论

例4.设定义在[-2，2]上的偶函数在区间[0，2]上单调递减，若f(1-m)＜f(m)，求实数m的取值范围。

分析：由函数的定义域知(1-m)∈[-2，2]，m∈[-2，2]，但是1-m与m到底是在[-2，0]、[0，2]的哪个区域内，不十分清楚，若就此讨论，将十分复杂，如果注意到性质“如果是偶函数，那么 f(-x)=f(x)=f(|x|)”，问题解答就简捷多了。

解：∵f(x)是偶函数，∴f(-x)=f(x)=f(|x|)，

f(1-m)＜ f(m) f(|1-m|)＜ f(|m|)

又当x∈[0，2]时，f(x)单调递减，

点评：本题运用了偶函数的一个简单性质，从而避免了一场“大规模”的讨论，将“曲径”变“通途”。值得深思。