“基于数学核心素养”平面向量解题的探索

向量是沟通代数和几何的工具，高考要求理解向量及运算的意义，能运用向量语言和方法解决问题。通过“分类构建”不同解题方向，激发学生探究向量专题的兴趣，从“几何图形的向量转化，立足于坐标系的坐标计算，向量和几何图形的结合”三个角度入手，巩固相关数学思想方法，让学生在掌握了基础公式法则的基础上，思维更多样，运用向量的“工具”意识更强，能更好更快的找到最优化解答向量问题的策略。

一、利用平面向量基底求解(化归思想)

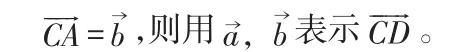
解：因AD=2DB，D为AB的三等分点。

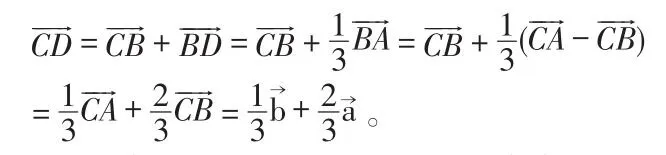
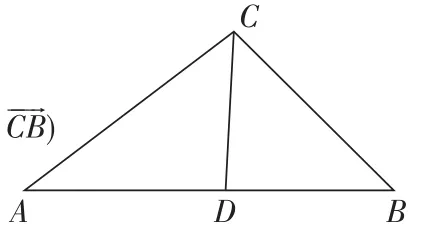
点评：本题充分利用平面向量基本定理，应用基本定理表示向量的本质就是利用三角形法则和平行四边形法则进行向量的加减或者数乘运算，借助图形特征将目标向量朝着边所在方向转化，完成用基底表示向量的任务。用基本定理解决问题的一般思路是先选择一组基底，运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决。而图形中线段的长度，特殊的点，是变形转化中要注意的地方。化归的过程，提高了“学生抽象和推理”核心素养。

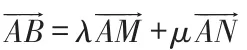
二、利用平面向量坐标法(数学建模)

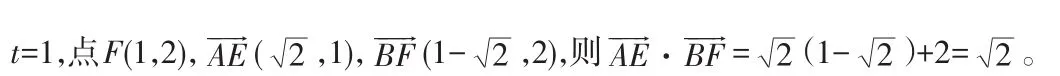
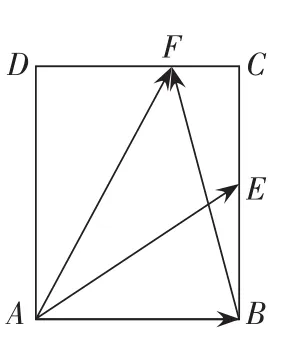
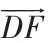
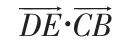
三、利用一般几何图形关系(数形结合)

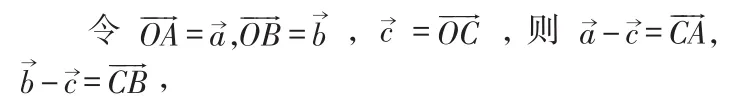
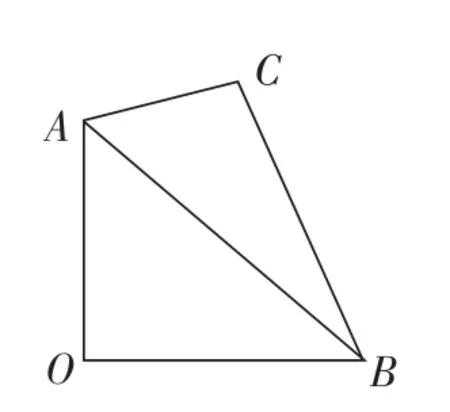
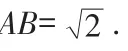
点评：本题通过对向量数量关系的分析，结合实际，画出满足题意的几何图形，加以几何分析，把向量的模对应的线段长度求出。充分说明了向量就是代数和几何的结合。这种方案的关键是利用向量的意义，脱去“向量外衣”，导出几何图形中点和线段的关系，通过几何法中距离，夹角，轨迹，最值等问题的解决，达到向量对应模，角等最值问题解决的目的。过程中垂直和平行关系的转化是重点。提升了学生“直观想象和推理”核心素养。

古希腊哲学家苏格拉底曾有“无人可做教师”的断言，他并不是否认教师的作用，而是强调真正的学习只有依靠学习者自己。本节构建的三个分类，不能完全代表向量应用的所有方向，只是抛砖引玉，提供给学生思考总结的角度，有针对性地复习整理。在向量解题思维训练的过程中，教师要在课堂上更多地站在学生角度“稚化”自己的思维，让学生有机会表达，有空间自省自悟，形成自我认知，确保更有效地解决问题。