基于障碍Lyapunov的自动作业船有限时间航向保持控制
2019-08-08戴小康孙太任刘志林赵德安
戴小康, 张 军*, 孙太任, 刘志林, 赵德安
(1. 江苏大学电气信息工程学院, 江苏 镇江 212013; 2. 哈尔滨工程大学自动化学院, 哈尔滨 150001)
工业化河蟹养殖要求在指定的水域内对饵料进行定位、定量且定时地均匀投放.自动作业船作为现代航运载体,有效解决了沿预定航迹进行动态均匀投饵的难题[1-2].自动作业船在导航系统的定位下,通过航向和航速的控制,实现从任意初始位置驶入预先规划的航线,并沿此航线动态均匀地抛洒饵料[3-4].自动作业船的主要工作方式为航向保持,其中均匀投饵的定位投放要求作业船的航向偏差不能超过指定范围,同时艏摇角速度不宜频繁变化,须小于指定的约束边界,故作业船的航向保持尤为重要[5-7].目前, 国内外对自动作业船的航向控制研究较少.Ruan等[8]采用模糊PID实现均匀投饵的直线航迹跟踪,但因未考虑船载投饵机产生的时变干扰,故鲁棒性较差; Zhang等[9]提出混合H2/H∞预测控制跟踪方案, 解决了航向约束和鲁棒性问题,但预测控制计算负荷较大.本文提出一种基于障碍Lyapunov函数(barrier Lyapunov function,BLF)的自动作业航向保持控制方法, 实现对航向偏差和艏摇角速率的上界约束, 并通过有限时间的分数幂项抑制风向和水流干扰的影响.
1 自动作业船的总体结构
自动作业船主要由船体、水草清理装置、投饵机和明轮驱动装置等部分构成, 其结构如图1所示,主要参数参见文献[1].为了在不增加船体体积的前提下充分利用船体空间,作业船采用单船体设计.船艏为切割与输送装置,用来切割并收集水草;船体中间为集草舱,用以存放已收集的水草;集草舱之后安装水草铺平装置,用来铺平水草,防止水草堆积;船尾放置投饵机,进行投饵作业.考虑到蟹塘的面积相对狭小,选择安装在船体两侧可正反转的明轮作为动力装置,避免水草缠绕.为了适应自动控制的需要,以蓄电池作为供电电源,采用电动推进器作为动力装置带动明轮旋转,从而提供船体前进所需的推动力[1].通过调节2个推进器的转速差, 使船体两侧的推力不同, 从而控制船体转向.本系统所有装置由容量为120 A·h的48 V锂电池驱动, 具有无污染、效率高和噪声小等特点.
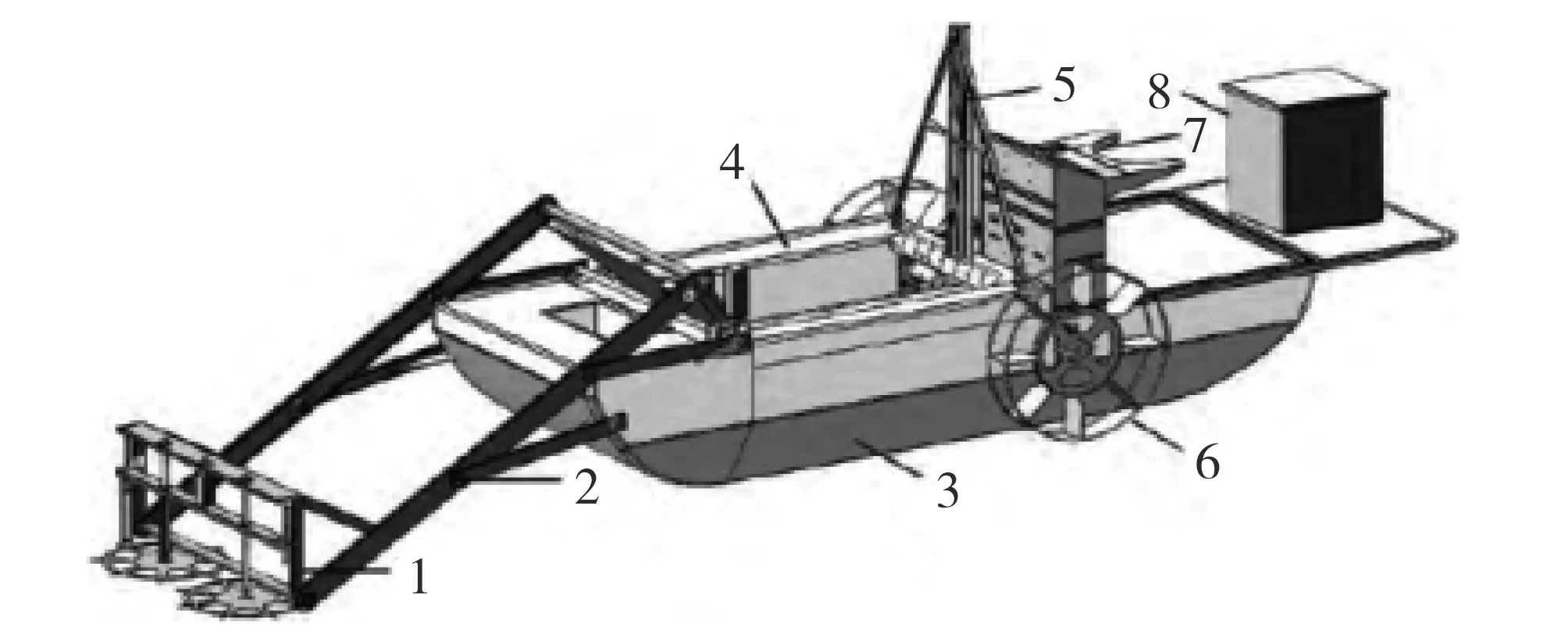
1. 水草切割装置; 2. 水草输送装置; 3. 船体; 4. 集草舱; 5. 水草铺平装置; 6. 明轮推进装置; 7. 操作台; 8. 投饵机图1 自动作业船的结构示意图Fig.1 Schematic diagram of operation boat
2 自动作业船的航向保持模型
河蟹投饵航迹是一种全覆盖式的路径,需要完全覆盖给定池塘区域,航迹主要包括直线行驶和转弯2个基本运动.为节省时间、缩短距离和降低能耗,假设作业船航是由预先设定的若干转向点构成,其中转向点之间可近似为直线的恒向线[9]; 同时,由于作业船的航速较低,现将作业船视为以固定的速度执行直线航迹航行, 故作业船的航迹方式主要是直线航向保持.Serret-Frenet坐标系下的航迹跟踪如图2所示, 坐标系的原点位于船舶重心在设定的目标航迹Ω上的正交投影,e为作业船的原点与坐标系的原点之间的距离,ψSF为目标航向,ψ为自动作业船的航向角.自动作业船共有6个自由度,但直线航向保持仅使用纵向速度、横荡速度和艏摇角速度3个量进行三自由度输入控制,忽略不计垂荡速度、横摇角速度和纵摇角速度.横荡速度很小,可以近似为0[7].假设纵向速度为常数,艏摇力矩与等效的明轮偏差角δ呈正比,且综合考虑建模误差和外部风向、水流时变干扰d, 在Serret-Frenet坐标系下作业船航向保持的误差动态方程为
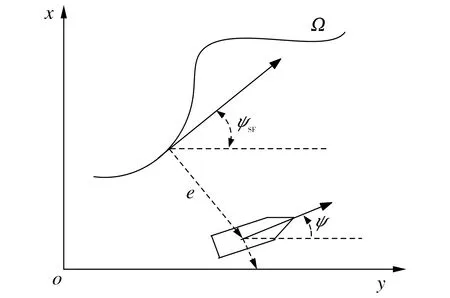
图2 作业船的Serret-Frenet坐标系Fig.2 Server-Frenet coordinate system of the operation boat
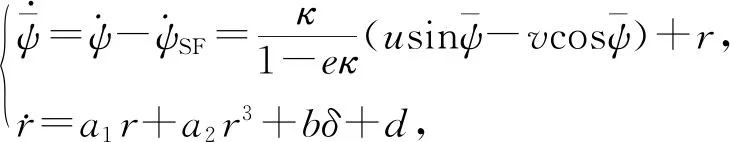
(1)

(2)
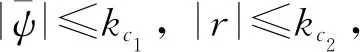
3 自动作业船的控制器设计
3.1 基于障碍Lyapunov 函数控制律
将作业船的航向偏差和艏摇角速度视为含有全状态约束条件的控制问题, 通过约束使得在航向保持中系统状态始终不超过约束上界, 从而实现作业船均匀投饵.采用基于动态面的BLF控制方法,通过有限时间控制的分数幂项提高系统抑制外来干扰的能力.
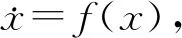
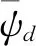
第一步: 选取对数型Lyapunov函数
(3)
由定义(1)可知,V1是障碍Lyapunov函数, |ψd(t)|≤A0,kb1=kc1-A0,A0为约束边界.对式(3)求导, 得到
(4)
(5)

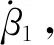
(6)
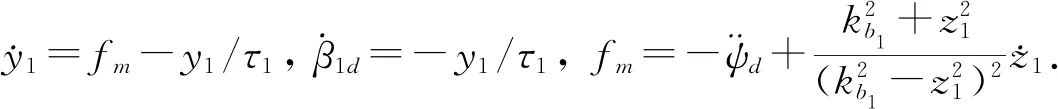
第二步: 选取对数型Lyapunov函数
(7)
由定义(1)可知,V2是BLF, |β1|≤A1,kb2=kc2-A1,A1为约束边界.对式(7)求导,得
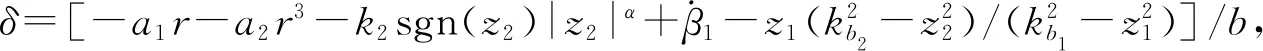
为了避免微分计算, 采用下述替代形式:
(8)
定理1对于有约束的航向控制系统(2), 在控制律(8)作用下闭环系统的输出信号严格有界,输出误差渐近收敛于零.
3.2 稳定性分析
设计系统(2)的Lyapunov函数为
(9)
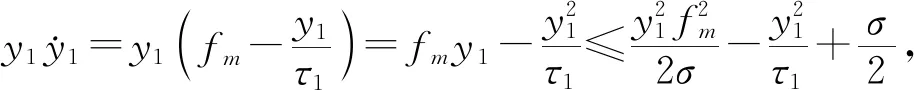
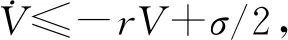
(10)
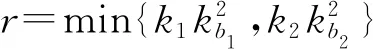
3.3 状态有界性

(11)
故信号z1(t)有界, 同理可推导z2(t)也有界.控制输入(8)的抗干扰理论分析类似文献[9],限于篇幅本文不予赘述.
4 仿真分析

图3 自动作业船的航向角Fig.3 Heading angle of aquaculture operation boat
图3为本文障碍Lyapunov函数约束控制方法与文献[7]反步法控制律进行航向控制的结果.由图3可见,反步法控制容易出现航向角违反约束上界的情况, 反向超调过大,收敛时间长,而本文方法航向保持收敛速度快,满足约束上界.
在无干扰情况下, 采用有限时间BLF控制律(8)与BLF控制律
(12)
的航向约束控制律对比, 结果如图4所示.由图4可见, 本文算法对期望航向实现较良好跟踪,收敛时间短, 航向偏差和艏摇角速度均满足约束上界.
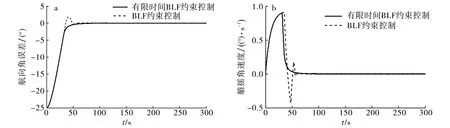
图4 无干扰下的作业船航向角(a)和艏摇角速度(b)Fig.4 Heading angle of operation boat (a) and operating boat’s rocking angular velocity (b) without interference
在有时变干扰d=sin(0.2πt)情况下,采用有限时间控制律(8)与BLF控制律(12)的航向约束控制律对比, 结果如图5所示.由图5可见, 本文方法的航向保持稳态误差小,艏摇角速度明显降低, 并且满足约束上界.

图5 有干扰下的作业船航向角(a)和艏摇角速度(b)Fig.5 Heading angle of operation boat (a) and operating boat’s rocking angular velocity (b) with interference
