基于纯无网格法三维对流扩散方程的并行计算
2019-08-08王星驰黄金晶
王星驰, 黄金晶, 蒋 涛
(扬州大学数学科学学院, 江苏 扬州 225002)
对流扩散方程是偏微分方程的一个重要分支,在流体力学[1]、生物医学[2]等领域有广泛应用,故对其数值计算方法的研究具有重要的理论和实际意义.基于网格类的方法已被广泛应用于此类方程的数值求解[3-4], 但其依赖于网格剖分的特性, 使其对高维问题的数值模拟比较困难,特别对非规则区域问题或区域上存在不均匀布点的问题[5].SPH[6-7](smoothed particle hydrodynamics) 作为一种纯无网格方法, 具有: 1) 易处理区域上不均匀布点情况或高维复杂区域的问题; 2) 算法易实现; 3) 具有分子动力学方法的相邻粒子并行搜索特性, 故该算法针对三维问题模拟时, 易采用基于MPI (multi-point interface)的并行技术来提高计算效率.本文基于核梯度, 拟通过改进传统SPH方法, 并结合MPI并行技术, 对三维对流扩散方程进行高效数值计算.
1 问题描述
考虑三维对流扩散方程
初始条件为u(x,y,z,0)=φ(x,y,z), (x,y,z)∈Ω; 边界条件为u(x,y,z,t)=φ(x,y,z,t), (x,y,z,t)∈∂Ω×(0,T], 其中t为时间,ν为黏度系数;bx,by,bz为对流系数, 假设bi<0(i=x,y,z);f,φ,φ为充分光滑的已知函数;Ω为长方体区域.
2 本文方法
2.1 CSPH-3D方法
为提高传统SPH方法的精度, 基于Taylor级数展开给出了一阶修正SPH方法[8].在传统SPH方法的数值模拟中, 第i个粒子对物理量f及其一阶导数f在空间位置r=(x,y,z)处的粒子近似式[1]为(f)i,α=∑jVj(fj-fi)i,αWij, 其中Vj表示第j个粒子对应的体积;i,αWij=∂Wij/∂xi,α, 式中Wij=W(|ri-rj|,h)为核函数,xi,α表示第i个粒子在位置r处的第α个分量,h为光滑长度, 它决定了W的支持域和影响域.

2.2 CSPH-3D方法的粒子搜索并行计算
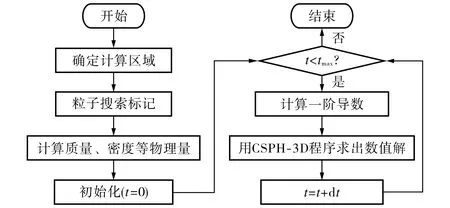
图1 CSPH-3D方法的流程图Fig.1 Flow chart of CSPH-3D method
在传统SPH方法模拟中,相邻粒子搜索在高维问题下会占用较大计算内存和较长CPU计算时间,因此本文根据模拟方程中粒子位置不动的特点,程序模拟物理量更新前对每个粒子的相邻粒子进行了标定,随后结合MPI并行技术[10],先对所有粒子进行编号,再根据CPU数量将粒子平均分配,最后同时进行计算,以此提高CSPH-3D方法模拟三维对流扩散方程的计算效率.该方法详细流程图如图1所示.为了提高计算效率,分别在计算质量、密度、一阶导数及最后计算函数值的更新中进行了并行优化.
3 主要结果
本文并行计算采用Red Hat Enterprise Linux5.8x86_64操作系统, MPI类型为Intel MPI Toolkits 4.0.3, 共有17个IBM BladeCenter HS22计算节点, 每个节点包括12个主频为2.67 GHz的Xeon 6C X5650 CPU.
3.1 有解析解的三维算例
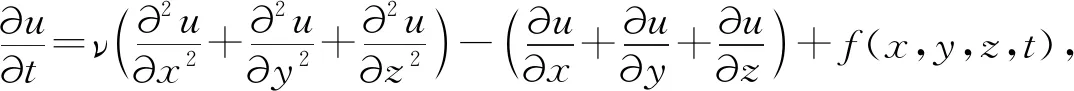
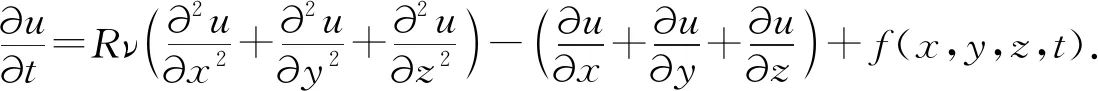
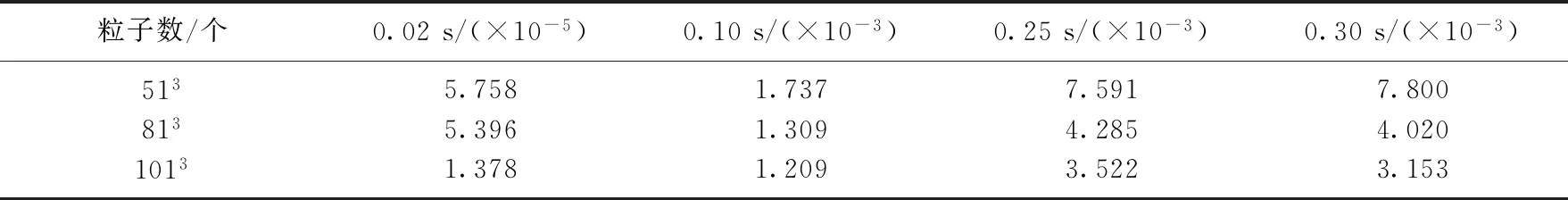
表1 在中心点(0.5,0.5,0.5)处数值解与精确解的绝对误差Tab.1 The absolute error between the numerical solution and the exact solution at the center point (0.5,0.5,0.5)

图2 不同黏度系数在沿x=y的变化曲线Fig.2 Change curve along the diagonal line x=y in different viscosity coefficients
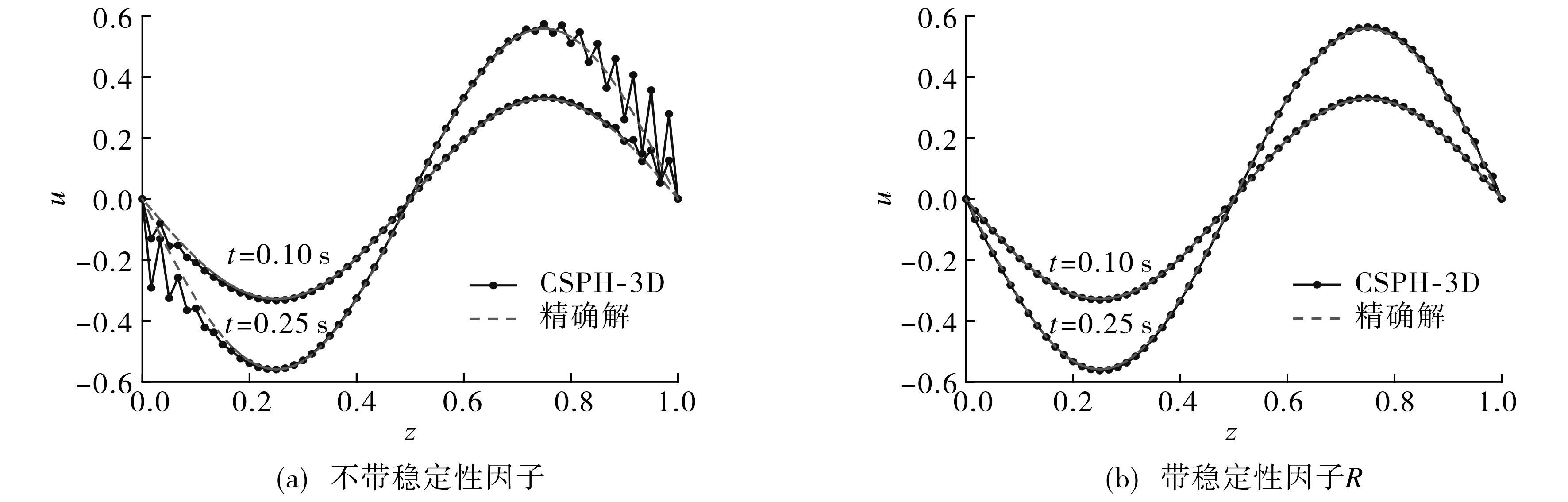
图3 黏度系数ν=0.1时, 不同时刻沿对角线x=y的变化曲线Fig.3 Change curve along the diagonal line x=y in different time for ν=0.1
表2给出了在813个粒子数下不同CPU数的消耗时间.从表2可以看出, 三维的串行程序占用了较大的内存和较长的计算时间,尤其在第一步粒子搜索时; 而随着CPU的增加,计算耗时迅速减少,计算效率得到提高.定义: 相对加速比τ=单节点上并行算法的消耗时间/N个节点上并行算法的消耗时间,本文每个节点上有2个CPU.结果表明, 相对加速比低于CPU个数增加的比值,这是因为随着CPU个数增加,从不同CPU上得到结果的通讯时间相对增加.
表3给出了不同粒子数、不同CPU数下的平均消耗时间.从表3中数据知, 当CPU数不变时, 随粒子数的增加,平均消耗时间也相对增加; 因此通过增加CPU个数进行并行计算可以减少计算机的模拟时间, 提高计算效率.
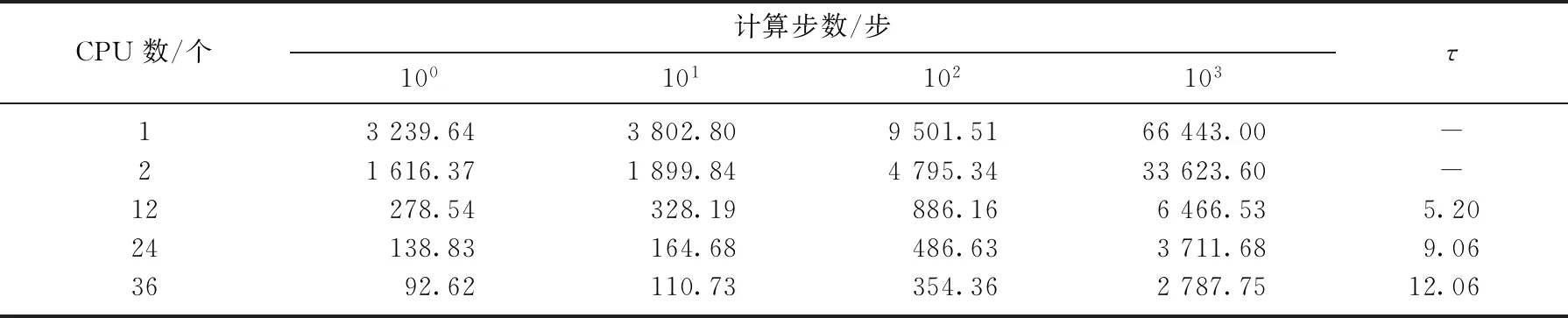
表2 粒子数为813时不同CPU数下不同计算步数的消耗时间Tab.2 Consumption time of different computational steps at different CPU number when particle number is 813 s

表3 不同粒子数、不同CPU数下的平均消耗时间Tab.3 Average consumption time at different particle number and CPU number s
3.2 无解析解的三维算例
考虑求解域为Ω=[0,1]×[0,1]×[0,1]的无解析解算例

图4 随粒子数增加沿z轴(x=y=0.5)的变化曲线Fig.4 Change curve along z axis(x=y=0.5) with the increase of particle number
其中源项为f(x,y,z,t)=π[2cos(2πt)sin(πx)+cos(πx)sin(2πt)]sin(πy)sin(πz) +π[cos(πy)·sin(πz)+cos(πz)sin(πy)]sin(2πt)sin(πx)+3vπ2sin(2πt)sin(πx)sin(πy)sin(πz), 黏度系数ν=10-3, 时间步长dt=10-3,采用36个CPU.
图4分别选取粒子数为513,713,1013,在t=0.25时沿z轴的数值收敛图, 可以看到除两端梯度有较小误差外均拟合较好.图5给出了粒子数为513时z=0.5的截面等值线.从图5可以看出,不同时刻截面的变化趋于一致.图4和图5结果表明,本文给出的方法随时间增长, 数值结果均有较好的收敛性和稳定性.
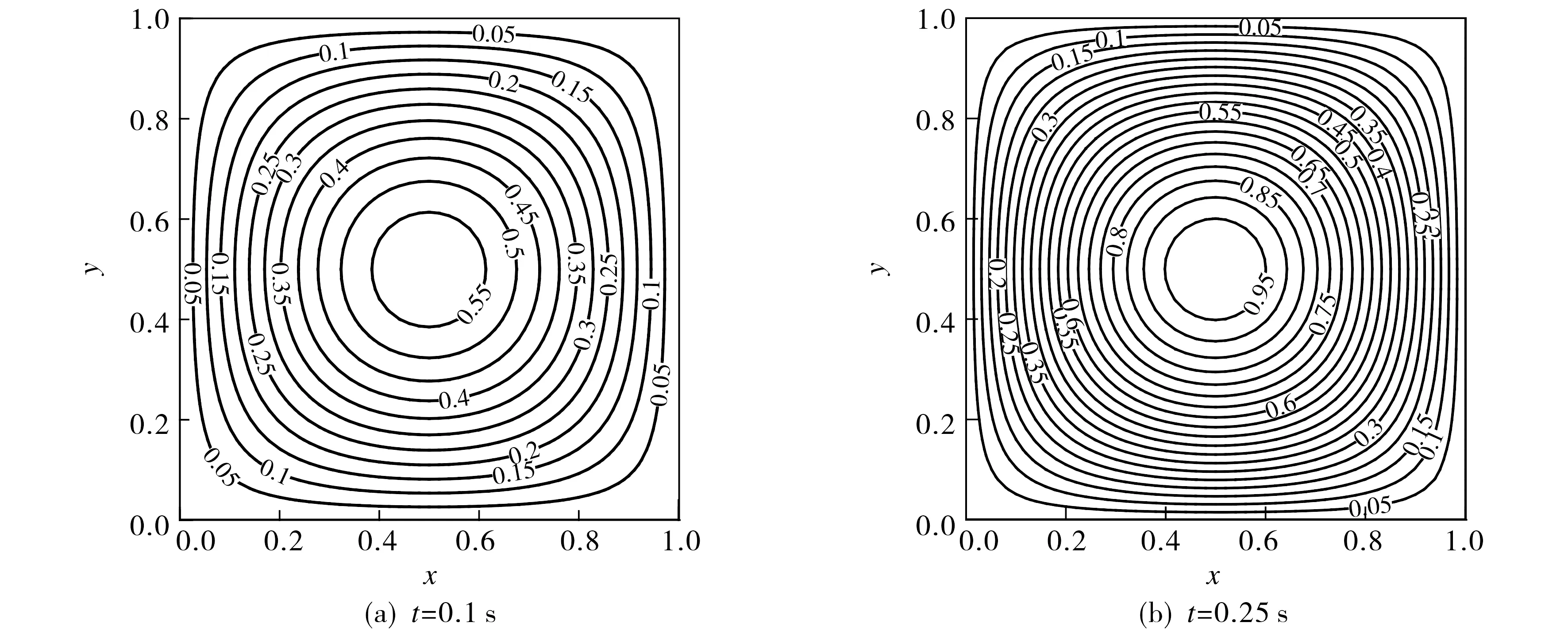
图5 513粒子数下不同时间的截面等值线图Fig.5 Cross-sectional isolines at different times for 513 particles
