基于盲数运算法土壤侵蚀模数计算研究
2019-08-08李根
李 根
(辽宁省农村水利建设管理局,辽宁 沈阳 110003)
1 概述
地区的水土流失程度受气候水文、地形地貌、土壤植被等自然条件以及人类活动等多方面因素影响[1],其主要形式分为面蚀、细沟侵蚀、重力侵蚀等。通常用土壤侵蚀模数表征一个地区水土流失严重程度,根据关于土壤侵蚀以及泥沙质量守恒等已有研究[2],平原等以水力侵蚀为主的水土流失量计算,可利用物质守恒定律,通过测算河流泥沙含量研究当地水土流失程度。
河流泥沙包括沉积泥沙、悬移质以及推移质,在不同参数的试验、测量及估算过程中,很多信息有多种不确定性,可以认为其在时间、空间上都是变化的[3],其中包括随机信息、未确知信息、模糊信息和灰信息。可将河流泥沙含量计算看成一个包含随机性、未确知性、模糊性及灰性的多种不确定性共存的大系统[4],这四种不确定性的信息被称之为“盲信息”[5]。本研究应用盲数理论,将影响河流泥沙含量的各个参数盲数化,通过盲数运算方法计算河流泥沙含量,进而测算地区土壤侵蚀模数。
2 盲数定义与计算
2.1 盲数的概念
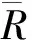
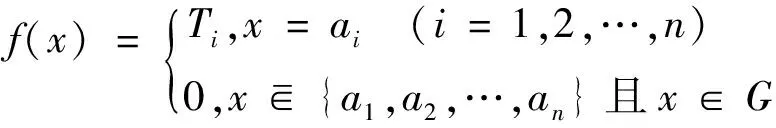
(1)

2.2 盲数的运算法则
有理灰数集G可以进行+、-、×、÷运算,设*为其中一种运算,设盲数
(2)
(3)
(1)盲数可能值计算
盲数A和B的可能值带边*矩阵,其中x1,x2,,…,xm和y1,y2,…,yn,分别称为A和B的可能值序列,如图1所示第一象限的矩阵称为A与B的可能值*矩阵。
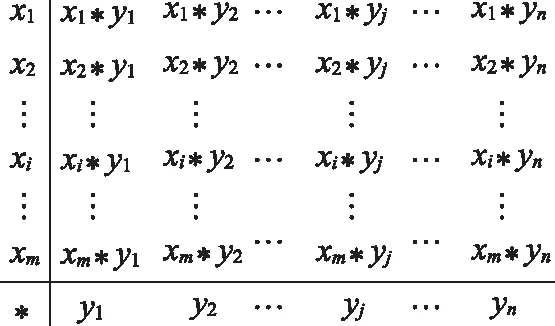
图1 A与B的可能值*矩阵
(2)盲数的可信度计算
如图2所示为A与B的可信度积阵。其中α1,α2,…,αm和β1,β2,…βn,分别称为A和B的可信度序列,图2的第一象限矩阵称为A与B的可信度积矩阵。

图2 A与B的可信度积矩阵
(3)盲数
假设C=A*B,则有
(4)

(5)
3 实例研究
3.1 研究区域
为提升研究模型的试验精度及实用性,本研究选择营口市大石桥市西部平原地区为研究对象,主要研究胜利河、劳动河、六股道河、新解放河四条河道对应小流域,四条河流均属于辽河水系,流域面积分别为93.4km2,河长分别为27km。
3.2 土壤侵蚀模数计算
计算研究区域的土壤侵蚀模数受限应计算一定时间内的水土流失量,包括计算沉积泥沙、悬移质以及推移质的含量。
(1)沉积泥沙
主要包括河道内以沉积为主要存在形式的泥沙和、垃圾、杂草、死亡生物以及生物排泄物等,主要采用试验方法求得[7]。沉积泥沙A的计算公式为:
D=γ×V×K
(6)
式中,γ—淤泥的容重,kg/m3;V—河道沉积泥沙的体积,m3;K—折算系数。
(2)悬移质泥沙
悬移质泥沙系受重力、水流等作用,在河水中悬浮运动的较细泥沙,在水流呈悬浮状态[62]。其近似值的计算:
S=Cs×Q×T
(7)
式中,S—全年河流悬移质泥沙的质量,kg;Cs—河流悬移质泥沙含沙量,kg/m3;Q—河流流量,m3/s;T—时长,s。
(3)推移质泥沙
推移质泥沙的运动包括移动、滚动、层移等形式,其含量占比很小,且较难通过仪器测得,实际运用中较多采用比值法计算推移质泥沙的含量[8],
P=w×S
(8)
式中,P—推移质泥沙质量多年平均值;w—推移质和悬移质的比值;S—悬移质泥沙质量多年平均值,kg。根据表1平原地区k取0.02,即P=0.02×S。综上,河流泥沙含量的计算公式为:
W=D+S+P=D+S+0.02×S=D+1.02S=γ×V×K+1.02×Cs×Q×T
(9)
土壤侵蚀模数为上式结果与流域面积的比值。

表1 推移质与悬移质比值参照表[9]
3.3 盲数模型建立
把河流悬移质含量Cs,流量Q,河底的淤泥容重γ,沉积泥沙体积V盲参数代入河流泥沙含量的计算公式,则计算河流泥沙含量在盲信息下的公式:
C={[γ1,γ2],Φ(γ)}×{[V1,V2],Φ(V)}×K+1.02×{[Cs1,Cs2],Φ(Cs)}×{[Q1,Q2],Φ(Q)}×T
(10)
因此,C为包含多个灰区间及其对应可信度的盲数,如果可知各盲参数的值,则能求得河流泥沙含量在盲信息下的值,即通过计算盲数C的均值,从而计算出河流泥沙含量的综合量化值。设Ci(i=1,2…,s)为河流泥沙含量的各种可能取值区间,αi(i=1,2…s)为各区间相应可信度值。
因为盲数C比盲数A、B的阶数高,可设盲数A={[γ1,γ2],Φ(γ)}×{[V1,V2],Φ(V)}×K,盲数B=1.02×{[Cs1,Cs2],Φ(Cs)}×{[Q1,Q2],Φ(Q)}×T。则河流泥沙含量E(C)=E(A)+E(B),即用E(A)和E(B)分别表示盲数A、B的均值。大大降低运算工作量。
3.4 数据计算
分别采集、统计、处理河流Cs、Q、V、γ的数据,将各个参数按照从小到大的顺序排列,选择合理的精度,划分数值区间,并按照数值落在各区间的频次计算可信度。其中胜利河的相应参数结果如下:
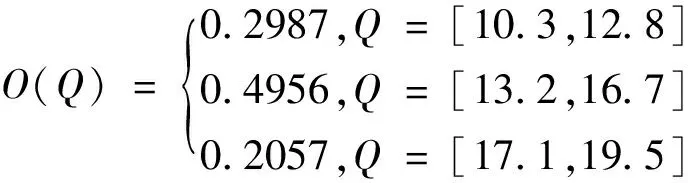
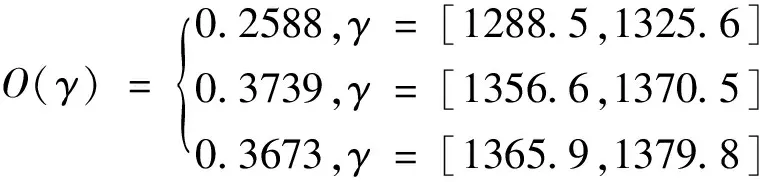
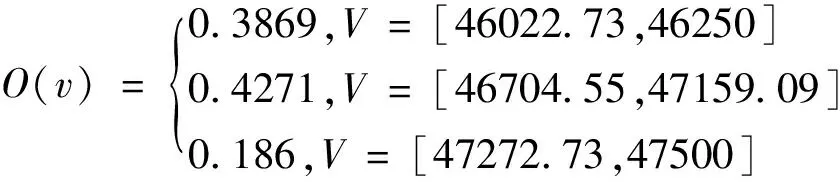
3.5 可能值及可信度计算过程
(1)盲数A的计算
根据盲数的运算法则,按照计算公式A=1.02×Cs×Q×T,计算盲数A的可能值带边积矩阵见表2及可信度带边积矩阵见表3。其中矩阵横向用x=Cs(kg/m3)表示,矩阵纵向用y=1.02×Q×T(m3)表示,其中T=365×24×60×60(s)。

表2 盲数A的可能值带边矩阵

表3 盲数A的可信度带边矩阵
将盲数A可能值带边矩阵中数值按照升序排列,同时对应盲数A可信度带边矩阵数值,得到表4。
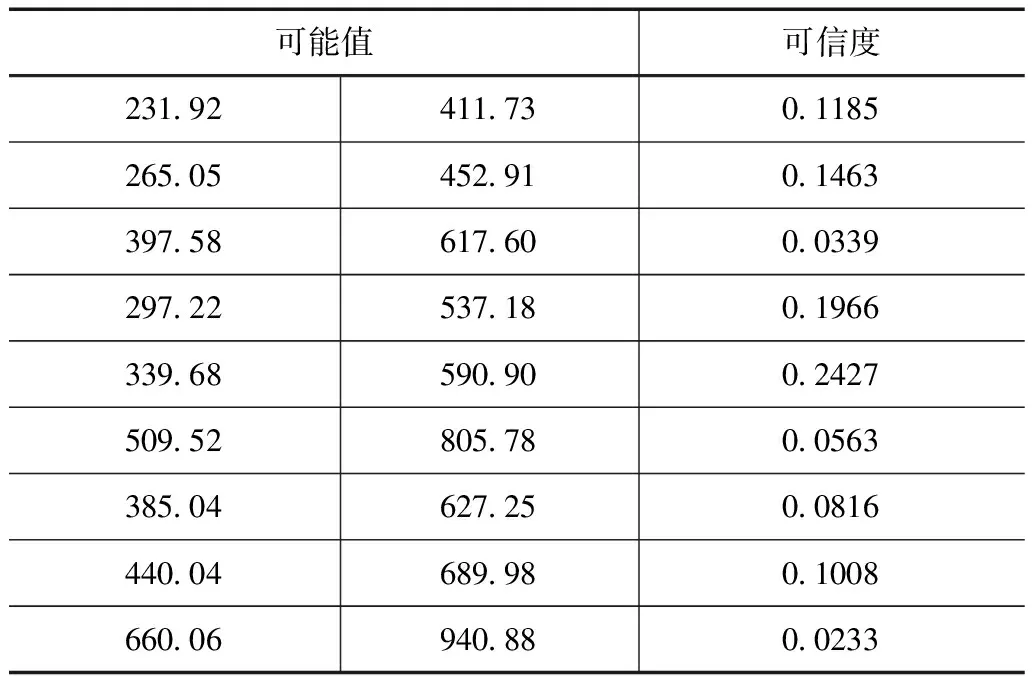
表4 盲数A的可能值及对应的可信度
(3)盲数B的计算
计算盲数B=γ×V×0.88,可能值带边矩阵横向用x=r(kg/m3)表示,纵向用y=V×0.88(m3)表示。盲数N(t)可能值带边矩阵的计算结果见表5。

表5 盲数B可能值及其对应的可信度
3.6 利用综合量化盲数均值计算河流泥沙含量
分别对表4和表5中每个灰区间取均值后进行求和,进而得出盲数C的可能值带边和矩阵见表6及可信度带边积矩阵见表7。
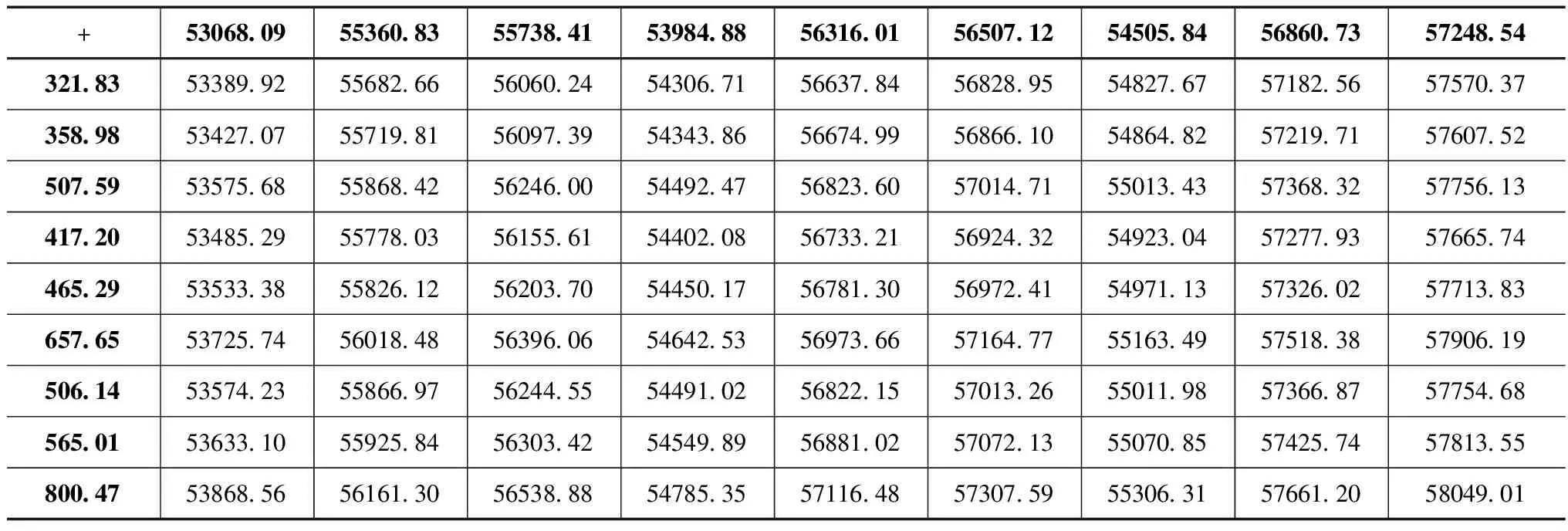
表6 盲数C的可能值带边和矩阵
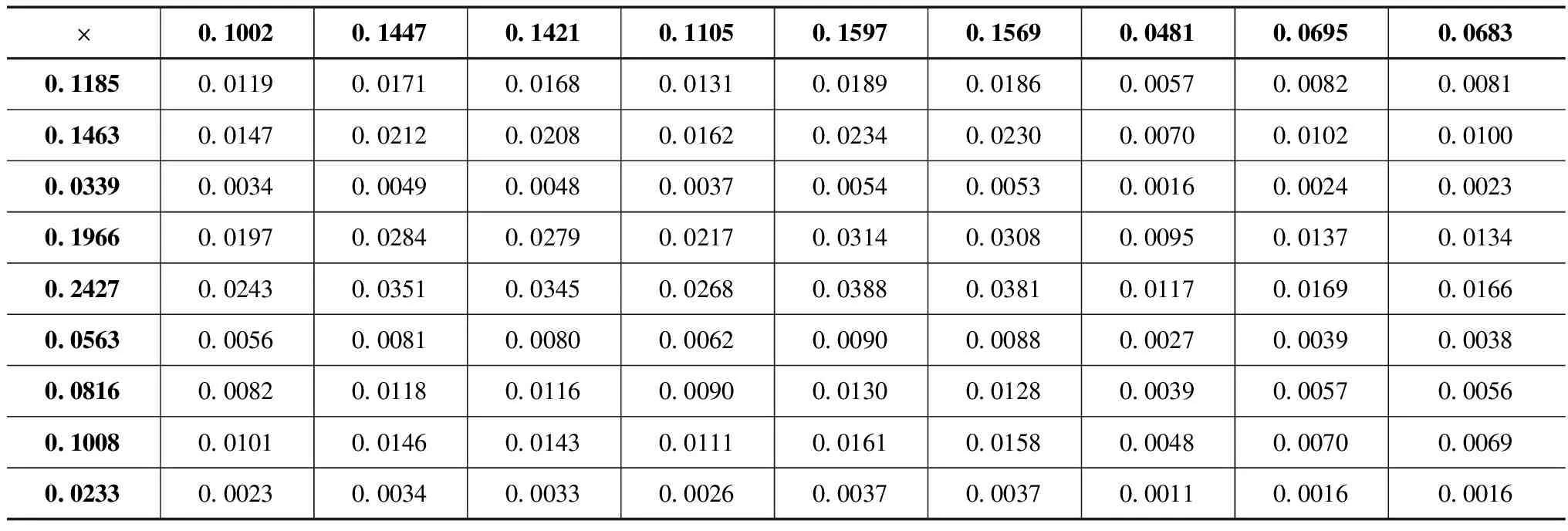
表7 盲数C的可信度带边积矩阵
根据表4求得淤积河道中悬移质的质量为456.74kg,根据表5沉积泥沙的质量为55557.15kg。胜利河泥沙含量(t)的可能取值区间为[52416.17,58616.52],对应的总可信度为1。胜利河流域面积为93.4km2,得出胜利河流域内土壤侵蚀模数的取值区间为[561.2,627.59]。
同理,将劳动河、六股道河、新解放河相关测量数据带入盲数模型,限于篇幅计算过程不再赘述,最终得出该地区的土壤侵蚀强度为[615.78,686.93],根据表8的分级标准[10],可知大石桥西部平原的区域土壤侵蚀模数对应水土流失程度属于轻度侵蚀。
3.7 计算结果对比分析
根据已有研究有关数据[11],大石桥西部平原的区域土壤侵蚀模数为500~2500t/(km2·a),可见计算结果比较合理。分析区域土壤侵蚀模数计算结果小于实际值,原因可能有三个方面:一是该盲

表8 水土流失土壤侵蚀模数分级标准
数理论建立在平原地区基础上,部分流失的土壤沉积在坡面的浅沟或凹地上;二是计算区域土壤侵蚀模数未考虑土壤被地表植被的拦挡导致滞留在坡面;三是本研究盲数理论的数据样本偏少,阶数偏低,好处是方便计算,但利用中值计算可能值时忽略了一些数据信息,一定程度降低了计算精度。
4 结语
(1)本文采用盲数理论计算河流泥沙量,测算区域土壤侵蚀模数,有效应对了沉积泥沙、悬移质以及推移质等数值存在的随机性、未确知性及模糊性和灰性,对区域水土流失状况评价及预测提供了一种方法。
(2)本文盲数理论模型主要针对平原等以水力侵蚀为主的情况,通过测算河流泥沙含量研究当地水土流失程度。如计算丘陵、山地等复杂地形时,为提升研究模型的试验精度及实用性,应修正相关参数。
(3)通过盲数理论计算区域土壤侵蚀模数过程发现,应尽量增加试验样本的数量,在确保计算量可行的基础上,尽量增加盲数的阶数,提升计算精度。
