使用计算几何学求多段线之交点

李 垚，夏富洲，刘富奎

(1.安徽省水利水电勘测设计院，安徽 合肥 230000；2.武汉大学水利水电学院，湖北 武汉 430072；3.中山市水利水电勘测设计咨询有限公司，广东 中山 528400)

在进行CAD的二次开发过程中，经常需要计算任意两条多段线之间的交点，然而多段线之间有可能有连续的交点，即某些区段是完全重合的，这时需要计算这个连续区间的2个端点坐标(射线重合只有1个交点)，另外也有可能是离散的交点。需要把这些连续的交点和离散的交点，用程序计算并保存下来。

1 多段线的数值表示

多段线的数值表示就是把一条多段线的几何信息用数字信息来表示。通常情况下，一条多段线是由线段和圆弧组成。考虑2种特殊情况，一种是当起始点终止点2个端点完全重合，并且凸度为0的情况。凸度概念，在AutoCAD里是把圆心角的四分之一的正切值(tan(θ/4))作为凸度，由于圆心角的取值范围为(-2π，2π)，所以凸度的取值范围(-1，1)，凸度的取值区间为开区间，因为当凸度接近-1或者1时，圆弧接近为一个圆形，当凸度为0时起始点终止点2个端点完全重合在同一直线上。另外一种是当起始点终止点2个端点完全重合，凸度不为0的情况。这2种情况在DXF文件中只可能出现在一条多段线的首端和尾端。下面把多段线的几何信息描述成数字信息。

1.1 圆弧

1.1.1圆弧的数据存储

圆的标准方程为(x-a)2+(y-b)2=r2里面有3个参数，即圆心的x坐标，y坐标以及圆的半径。表示一个圆弧，需要有圆弧的起始点(x1，y1)、终止点(x2，y2)、凸度d。为方便交点的计算，同时准确表示一段圆弧需要有8个参数。可以用一个3×3的数组来存储圆弧的信息，这样还多出一个存储单元，可以把起始点和终止点的长度m存储到这个单元里。数据的存储如下：

1.1.2圆弧的相关参数求取

(1)求圆弧的半径

已知DXF文件提供了圆弧的起始点P1(x1，y1)、终止点P2(x2，y2)、凸度d共5个参数，以这5个参数推导出圆弧的圆心坐标及圆弧的半径。

由圆的参数方程有：

x1=a+rcosφ

(1)

y1=b+rsinφ

(2)

x2=a+rcos(φ+θ)

(3)

y2b+rsin(φ+θ)

(4)

由凸度的定义得到圆心角的计算公式：

θ=4tan-1d

(5)

(式1-式2)2+(式3-式4)2得：

(x1-x2)2+(y1-y2)2=2r2-2r2cosφcos(φ+θ)-2r2sinφsin(φ+θ)=2r2-2r2cosθ

则

(6)

(2)求圆弧的圆心

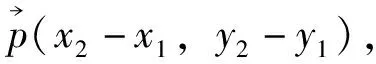
(7)

(8)

联立式(7)式(8)得到

λ=-0.5

(9)

1.2 线型对象

1.2.1线段的数据存储

1.2.2射线的数据存储

2 求交点

由于多段线是由线段、圆弧组成，当考虑多段线的端点沿其切线方向的射线时，多段线之间的交点最多会出现6种情况(线段和线段、圆弧与圆弧、射线和射线、线段和圆弧、线段和射线、射线和圆弧之间的交点)，下面主要对圆弧与线段情况的交点计算方法进行讨论，其余5种情况和这种情况类似。

该方程为一个关于s的一个一元二次方程：

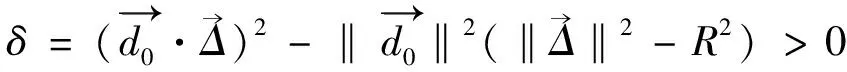
以上获得的只是线段和圆的交点坐标，在一条多段线里只有线段或者圆弧，是没有圆的。因此要进一步根据圆弧端点和线段的关系去取舍点。

如图多段线ABCD是由2条线段和一条圆弧组成。线段和多段线ABCD的位置关系主要可以分成6种情况进行考虑。如图1所示。

(1)线段和圆O没有一个交点，如线段m1与圆O的位置关系。

(2)线段和圆O实线部分有1个交点，如线段m2与圆O的位置关系。

(3)线段和圆O实线部分有2个交点，如线段m3与圆O的位置关系。

(4)线段和圆O的实线部分虚线部分各有1个交点，如线段m4与圆O的位置关系。

(5)线段和圆O的虚线部分有2个交点，如线段m5与圆O的位置关系。

(6)线段和圆O的虚线部分有1个交点，如线段m6与圆O的位置关系。

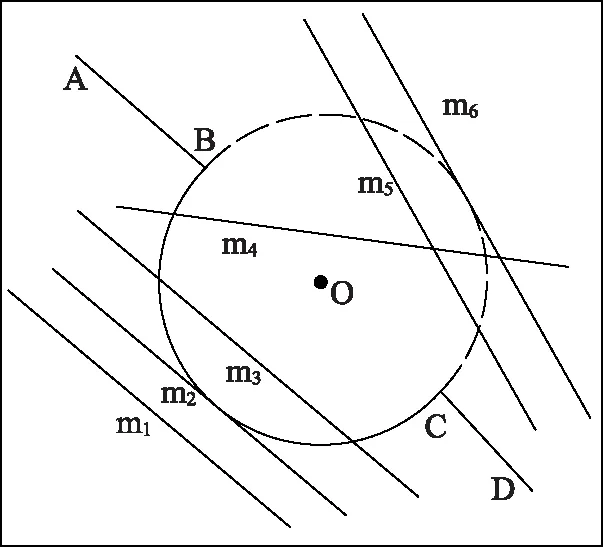
图1 圆弧和线段的交点

对于任意一个在圆O实线部分上的点，需满足以下条件：

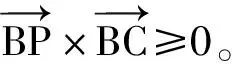
通过以上2种情况能够将线段与圆弧的交点成功筛选出来。

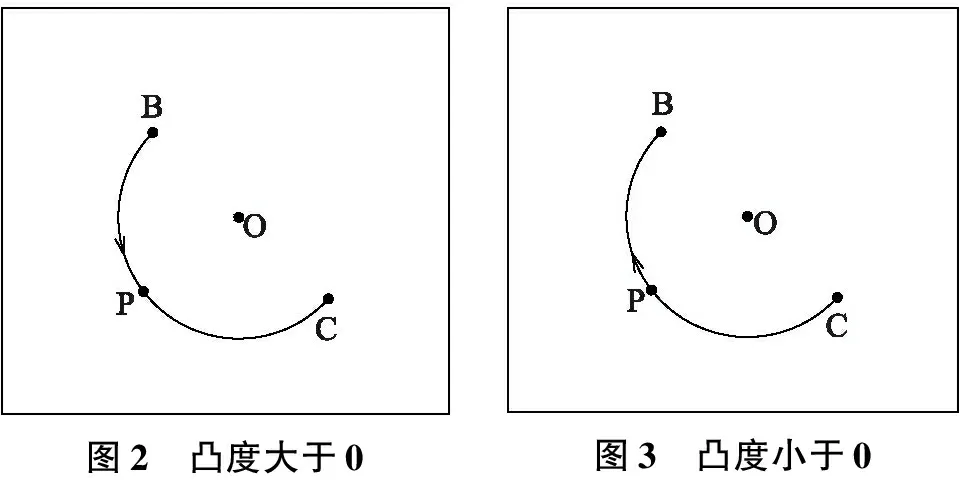
图2 凸度大于0图3 凸度小于0

3 工程应用

实际在AutoCAD二次开发的计算机语言中有求交点的函数，这个函数的求交点结果不是很稳定，有的情况即使有交点，也无法计算出结果，有的情况计算出来的点存在多个一样的情况，另外该函数在求交点时，必须是AutoCAD的dwg文件中的两条已经存在的多段线。本文所提到的多段线求交点的方法，恰好能够弥补以上不足。

智能识别桩号点，在堤防的平面线绘制过程中，能够将横断面图设计线的特征点准确的绘制到平面图中。但是每两个桩号线之间都是用线段直接连接，如图4所示中的拟生成线。为了让平面图中的设计线能够符合地形，需要对平面线进行调整。目前已经开发出一套软件，可以根据地形先调整好一条平面线，如图4中的被模仿线(m0)，然后其余线条可以根据被模仿线的形状和走势自动生成。这中间就会产生一个问题：怎样保持拟生成线(m1、m2、m3)在桩号线上的位置不变，同时桩号线与桩号线之间的线段能够根据被模仿线的形状和走势智能调整。上面介绍的求交点的方法能够解决这一问题，具体算法：

第一步被模仿线和桩号线1、2求交点，将这些点标记为不可改变点，分别记为pt1、pt2。

第二步把pt1、pt2在被模仿线上之间的一系列点点ptn截取下来，并记下其凸度、法线方向向量等线型特征。

第三步拟生成线和桩号线1、2求交点，将这些点标记为不可改变点，分别记为pt3、pt4。

第四步根据第二步获得的线性特征，在pt3、pt4之间，把线型自动智能生成。

最后通过对被摸仿线线型的模仿，图4中的拟生成线，最后转变成如图5所示的生成线，程序的模仿线的效果还是不错的。通常堤防设计过程中有7条线需要绘制。现在使用此程序，只需绘制其中一条线，其余6条线能够智能生成，效率相当于提高3～5倍。

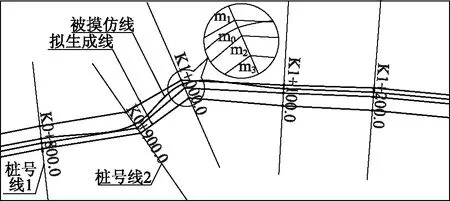
图4 多段线被模仿前

图5 多段线被模仿后

4 结论

本程序使用Lisp语言编制而成，测试时，使用2条都有10段的多段线，执行500次循环运算，花费时间7.29秒，平均每次花费时间0.015s，同时计算结果比较理想。求交点程序在CAD的二次开发中需要经常用到，然而AutoCAD提供的函数只能在2条多段线都存在于AutoCAD模型空间中的情况下才能进行求交点计算，有时候甚至无法求出多段线的交点。本文提出了使用计算几何学计算交点的具体方法，并编制了计算机程序。在堤防平面图设计过程中需要智能识别桩号位置的点，本程序的成功编制很好的解决了这个问题。本文介绍的应用程序已经在《无为县五千亩至万亩圩口除险加固工程(Ⅱ期)》《2015年度拦路港堤防除险加固工程》《巢湖流域牛屯河防洪治理工程》等项目中得到很好的应用。。