基于多索引树的阴影光线遍历算法

梁 晓，黄 韵

基于多索引树的阴影光线遍历算法

梁 晓1，黄 韵2

(1. 西南石油大学计算机科学学院，四川 成都 610500；2.西南石油大学材料科学与工程学院，四川 成都 610500)

阴影光线求交计算是光线跟踪的重要计算瓶颈。然而，构造一棵能有效剔除阴影光线冗余求交计算的标准树结构仍然十分困难。为区分遮挡和非遮挡的阴影光线，提出一种基于多索引树的遍历方法，在节点中增加提升遍历速度的索引。首先，针对遮挡光线为尽快与图元相交的遍历特征，选择性的将位于叶节点上、对光线遮挡概率高的图元索引到中间节点，促使光线提前在树中层停止搜索。其次，针对非遮挡光线为尽快搜索最邻近节点的遍历特征，为底层节点建立邻接索引，减少节点搜索空间。利用帧间相关性预测遮挡类型，采用相应遍历方法进行针对性的加速。相比专有树结构的遍历算法，该算法将遍历时效率提升20%以上，具有更好的遍历性能，且预计算时间更少。

光线跟踪；阴影光线遍历；层次加速结构；分支预测

光线跟踪，是当前应用最广泛的真实感绘制方法之一，广泛应用于影视特效、工业设计、游戏等领域。其原理是通过递归的追踪从视点投射到三维虚拟场景中的主光线、阴影光线、二次光线，以产生高级光照效果。其中，阴影能有效反映物体的形状、空间关系、光源位置等信息，被认为是最重要的全局光照效果之一。对于复杂场景，阴影光线数量占到了场景中所有光线的绝大部分，即使采用加速结构，例如KD-Tree[1]、BVH[2]，阴影光线的快速求交计算仍然是光线跟踪领域的重要难题。

经典的阴影光线遍历算法中存在大量冗余的求交计算。阴影光线仅需计算与场景的“任意交点”，而经典算法按照光线方向从前向后的顺序最终计算的是与场景的“最近交点”。通常，最近的图元并不一定是求交计算量最小的图元。

阴影光线遍历的加速方法可分为：①基于已有树结构的分支预测遍历方法[3-4]。该方法与主光线、二次光线共用加速结构，评估子树的遍历代价，并让光线优先与预测代价更小、或具有更低深度的子树求交。但仅能提前终止遮挡阴影光线的遍历过程，无法减少非遮挡阴影光线的冗余计算，通常后者比前者的计算量更大。②针对阴影加速而设计的专有树结构[5]，用于阴影光线遍历。尽管可同时降低2类阴影光线的求交计算量，却需要额外产生新的树结构，预计算时间非常长，内存开销增加显著。

以上2类方法都是在标准树结构上计算求交测试更少的遍历路径，其本质是相同的。标准树结构是一棵二叉树，为便于自上而下、逐步求精的遍历，中间节点记录直接子节点索引，叶节点记录图元索引。然而，对于阴影光线遍历，构造一棵能有效剔除冗余求交计算的标准树结构，不仅预计算量大，而且十分困难。因为树中节点仅具有一种索引类型，并用于描述严格的层次包含关系，本身仅适用于减少以求“最近交点”为目的的光线求交计算。实际上，阴影光线分为遮挡和非遮挡光线2类，前者以尽快与图元相交为目的，后者需要造访整个树空间，以尽快搜索最邻近节点为目的。因此，若在现有树结构中，以索引的形式增加提升遍历速度的多类节点关系描述，不仅能够剔除冗余的求交计算，并且具有较小的计算量。

本文提出一种基于多索引树的阴影光线遍历算法，利用遮挡和非遮挡阴影光线各自的遍历特征，分别为节点增加图元索引和邻接索引来降低冗余求交测试。对于遮挡阴影光线，选择性的将位于叶节点上、对光线遮挡概率高的图元索引到中间节点，促使光线提前在树中层停止搜索。对于非遮挡阴影光线，为节点建立邻接索引，用于访问最近邻节点，大幅度降低节点的搜索空间；并按需建立邻接索引，减少索引产生的内存开销。同时利用帧间相关性预测光线的遮挡类型，使用对应的遍历加速算法，降低相交测试开销。实验显示，对于复杂场景，算法在阴影光线遍历时效率提升20%以上。相比专有树结构算法，具有更好的遍历性能，且预计算时间和内存开销仅是后者的21%和48%。

1 相关工作

1.1 加速结构的构建

在树结构中，选择节点分割平面是影响加速结构质量的重要因素。通常，预测光线的遍历代价，即光线与节点、图元的相交代价，作为产生最优分割平面的指导。最具代表性的是表面积启发式代价模型(surface area heuristic，SAH)[6]。SAH算法对场景进行了若干简化假设，包括光线在空间均匀分布，不会因为与图元相交而终止传播等。给定节点，其遍历代价表示为

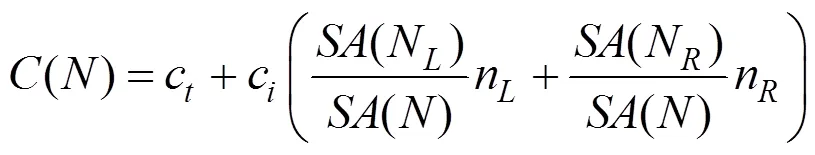
其中，c和c分别为节点、图元相交测试代价；n和n为左、右节点N和N的图元数目；()为包围盒表面积。在构建时，算法在候选分割平面集合中选择具有最小代价值的平面作为当前的最优划分，并产生子节点。

SAH算法计算量很大，文献[7]在分割轴开区间进行离散采样来近似遍历代价。此外，基于多核CPU[8]、基于GPU的构建算法[9]解决节点计算负载均衡、局部访存等问题，从不规则层次构建算法的并行化中来获取大量性能提升。

SAH算法中的诸多简化假设降低了预测代价的准确性。为此，研究者分别对KD-Tree和BVH提出了不同的高质量树构建方法。文献[10]采用模拟退火思想搜索最优分割平面，避免局部最小值。对于BVH，通常采用“快速构建，逐步优化”的思想提高树质量。文献[11]搜索构建质量较低的节点，并旋转节点来更新结构。文献[12]选择低质量节点及分支，并在全局空间中搜索新插入位置。

为减少阴影光线遍历代价，文献[5]提出阴影光线代价模型(shadow ray distribution heuristic，SRDH)，建立一棵面向阴影光线遍历的专用树结构，能够减少遮挡和非遮挡2类光线的冗余测试，却伴随着巨大的时间和内存开销。

1.2 加速结构的遍历

针对GPU内存存储限制，文献[13]提出无栈遍历算法—KD-Restart和KD-Backtrack，通过增加大量冗余的节点访问操作来移除对栈的依赖。文 献[14]实现了基于KD-Tree的短栈遍历方法，对共享分割面的中间节点创建邻接索引，遍历效率提高了17%以上，但内存增加3倍以上。文献[15]在BVH上实现短栈遍历，利用重启跟踪降低入口点搜索的代价。

阴影光线的遍历不受“从前向后”的顺序约束，分支预测方法能快速搜索遮挡图元。文献[3]建立阴影光线代价模型，总是优先遍历代价较小的节点。文献[4]提出表面积遍历策略组合(surface area traversal order，SATO)算法，将遍历序列优先分配给有特殊几何特征的节点，特征包括包围盒表面积、图元面积和数目。该算法预计算快，遍历速度优于其他启发式算法，但每种策略有不同的适应场景。以上算法仅能降低遮挡光线的遍历代价，而本文修改了树结构，使用较少的预计算，同时降低了遮挡和非遮挡光线的遍历代价。

2 本文算法

在标准树结构上，阴影光线从树根节点出发，自顶向下的搜索遮挡图元。一旦与图元相交，遍历过程立即停止，判定为遮挡阴影光线(简称遮挡光线)；若遍历完树空间都没有与任何图元相交，判定为非遮挡阴影光线(简称非遮挡光线)。然而，2类光线具有不同的求交特征，其在标准树结构上进行遍历时均存在冗余相交。本文提出一种基于多索引树的阴影光线遍历算法，利用2类光线的遍历特征，为节点增加图元索引和邻接索引来降低冗余的求交测试，如图1所示。

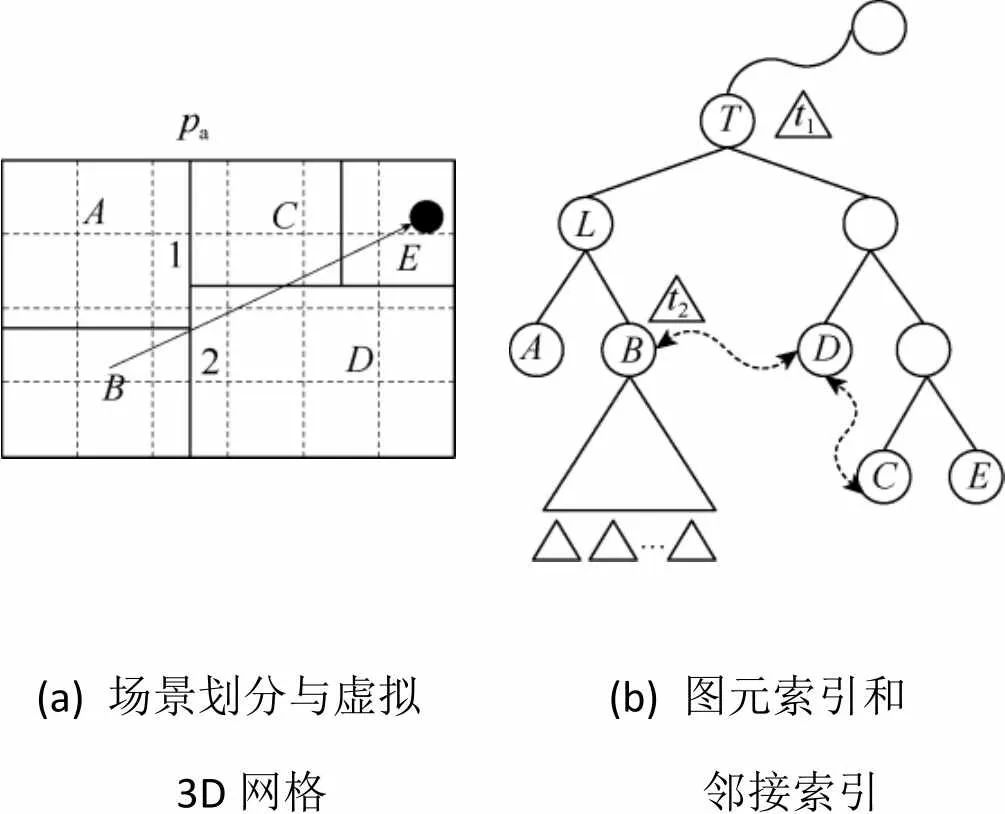
(a) 场景划分与虚拟 3D网格(b) 图元索引和 邻接索引

对于遮挡光线，提出一种基于图元索引的遍历方法。从叶节点选择光线相交概率大的图元直接索引到适当的中间节点，使遮挡光线提前在树中层终止搜索。该图元称为中间图元。如图1所示，给定子树，t、2为叶节点上的图元，并相对于其他图元具有更高的相交率。将图元t、t直接索引在节点和，使得进入到该类节点光线与t和t相交而提前终止搜索。

对于非遮挡光线，为底层相邻节点添加邻接索引，使光线利用邻接索引直接进入下一个节点，避免了大量自顶向下的搜索测试。其中，为每个节点添加邻接索引将大幅度增加内存开销。然而，与其他类光线不同，阴影光线的分布是不均匀的。如图1所示，光源位于节点，若节点是主光线不可见的，并不会产生阴影光线。因此，节点的所有邻接索引对阴影光线遍历没有贡献。为此，从光源所在节点出发，逆向的为相邻节点建立索引。

2.1 基于图元索引的遍历方法

为使遮挡光线在遍历过程中提前与潜在相交图元进行测试，本文算法选择图元并索引在中间节点。中间图元的选择以及新的索引位置，对遍历代价的影响非常关键。所有进入带图元中间节点的光线都将与该图元进行相交测试。若大部分相交测试失败，产生额外的相交代价将大于遍历收益。为此，在不同索引位置评估候选索引图元引入的遍历开销差，以选择合适的子树来索引图元。

(1) 选择候选图元。理想的候选图元能够与更多的光线相交。直观的、在光线均匀分布情况下，图元相对光源的空间角越大，可能遮挡的光线就越多。为此，本文算法设置包围盒表面积阈值，若图元的包围盒表面积与场景平均图元包围盒表面积之比超过阈值，加入候选图元队列。阈值取值随场景图元形状的规则影响，通常设为[0.45~0.60]。

(2) 给定子树和候选图元，算法评估新增图元在子树产生的遍历代价。新增图元索引后，子树的遍历代价主要包括与中间图元相交、并终止搜索的光线遍历代价，和与中间图元没有相交、并需要进入下层子树并继续测试的遍历代价，即

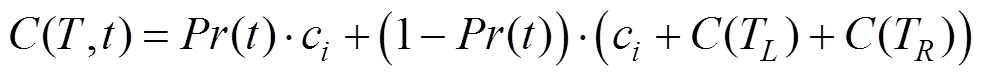
其中，()为新增图元后的遍历代价；()为图元与光线相交的概率，由图元包围盒和节点包围盒表面积之比表示；(T)和(T)分别为左、右子树的遍历代价，并使用SAH模型计算。

由于式(2)计算的是本地代价，不能用来选择最佳索引位置。在此基础上，用图元索引前、后的遍历代价之比，来评估图元在不同子树中的遍历代价降低率。考虑到图元索引的深度越低，对全局遍历代价的影响越大，且影响是非线性的。引入受索引深度变化的指数曲线来描述遍历代价降低率，即

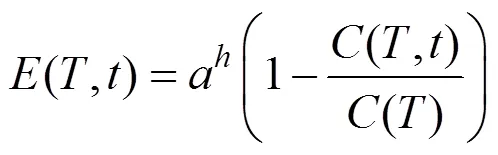
其中，通常取值为0.6；为索引深度。由于索引位置过高或过低，不会大幅度降低遍历代价，通常将索引深度控制在树的中间层内。

为减少中间图元产生的额外图元相交测试，本文算法谨慎的选择图元并索引中间节点。对每个候选图元，利用式(3)自底向上的评估遍历代价降低率，从中选择具有最大收益的节点作为其最佳索引位置，当收益率大于预定法阈值，将图元索引到对应节点上。本文算法仍然为中间图元保留了树底层的索引，以降树结构修改的代价；并为光线记录了已经执行过测试的中间图元，以避免冗余测试。文献[16]算法也将图元索引在树中，但本文与其不同之处在于：图元索引的目的不同，前者用于降低内存开销，而本文旨在提高遮挡光线遍历效率；图元选择的方法不同，前者需要大量的重构计算来选择最佳图元以及索引位置。

2.2 基于邻接索引的遍历方法

本文为底层节点建立邻接索引，用于访问下一个节点。邻接关系是指2个节点的轴对齐包围盒具有共面关系。邻接关系是指2个节点的轴对齐包围盒具有共面关系。然而，为每个节点创建邻接关系会导致树结构增加3~4倍以上。由于阴影光线的起点以及光源位置是已知的，利用阴影光线分布，按需建立邻接索引以减少冗余的索引关系。

步骤1.标记主光线可见区域。标记底层节点的可见性，若包含可见的图元，该区域是可见的。

步骤2.建立虚拟网格作为辅助结构，将可见区域映射到网格中，判断2个可见区域是否具有邻接关系。如图1(a)所示，将每个可见区域包围盒所在平面映射到网格，得到体素集合。体素1包含的节点和，体素2包含节点和。当且仅当2个节点在同一体素时，则存在潜在的邻接关系。

步骤3.从每个光源所在节点开始搜索，逆向的建立节点间的邻接索引。首先将光源所在节点加入到队列中；其次，取出队列中的首节点，对所有邻接节点按照步骤4判定邻接面，并将该所有邻接节点加入到队列尾部；直到队列为空。

步骤4.比较2个节点的轴对齐包围盒的最值，判定产生邻接关系的包围盒面，并将对方节点地址记录到相应的索引分量上。例如相邻节点和包围盒的最值有如下关系，若min.和min.相同，的right面与的left面共面。

若帧间变化剧烈，部分区域的邻接索引可能并不完整。如图1(a)所示，若第帧中节点不可见，其邻接索引为空；在第+1帧中，若是可见的，出射的阴影光线与右侧面相交后，将没有邻接索引用于直接访问下一个最近节点。对此类情况，需要从根节点开始进行递归测试。然而，实验数据显示，此类区域和光线非常少，并不影响遍历性能。

2.3 基于多索引树的遍历方法

利用帧间和空间相关性，预测光线遮挡类型，调用相应方法进行针对性的遍历加速。将屏幕划分为×区域，在第帧中，每个区域选择1条光线跟踪并记录是否与图像相交的遍历结果；在第+1帧中，查询上一帧在当前子区域的采样结果，用于选择遍历算法。由于是先预测类型再进行遍历，可能存在对非遮挡光线使用了图元索引遍历，对遮挡光线使用了邻接索引遍历。前者不会增加计算步骤；后者可能会带来更多的遍历步骤。若预测准确，这类光线非常少，并不会影响整体遍历性能。

3 实验结果与分析

实现了基于多索引树的阴影光线遍历算法，用于基于KD-Tree的光线跟踪绘制。测试平台为Intel(R) i5-3230 CPU，8 G内存，NVIDIA GeForce GTS 450图形显卡。本文算法与标准遍历算法、SATO[4]和SRDH[5]3种算法进行对比。选择具有不同几何特征以及阴影光线遮挡率的测试场景，如图2所示，并以1024×1024分辨率进行绘制。

为衡量算法对遍历代价的影响，分别测试了遮挡和非遮挡光线的相交测试数，见表1，标准遍历算法是测试基准。SATO算法没有改变非遮挡光线的节点、图元相交测试数，本文算法没有改变非遮挡光线的图元相交测试数，其对应测试项均标记为空。

(1) 评估算法对遮挡光线遍历性能的影响。由表1可知，本文算法降低了所有场景的相交测试数，节点、图元相交测试数分别减少了18.5%~31.7%和0.4%~33%。与SATO算法相比，本文算法在2项相交测试数上均能够获得更高的降低率。当且仅当最近图元位于更深子树时，SATO算法将优先与其他分支上、遍历代价更少的图元进行测试，其减少的遍历代价来自于2个分支的深度差产生节点相交测试计算量。若场景不满足此条件，并不能明显的降低遍历效率。而本文算法并不受最近图元分布的影响，将潜在相交图元提前索引在树中层，剔除了索引位置所在节点以下子树的相交测试，减少的计算量通常大于前者。此外，与SRDH算法相比，本文算法仍然能够获得近似甚至更高的降低率。

(a) Bedroom(4个点光源，光线数为3.9 M，遮挡率为74.3%，图元数为361 754)(b) Sponza(1个面光源，采样率为4，光线数为4.1 M，遮挡率为72.2%，图元数为66 450)(c) Conference(1个面光源，光线数为8.3 M，遮挡率为34.3%，图元数为282 755)(d) FairyForest(2个面光源，采样率为2，光线数为4.7 M，遮挡率为81.3%，图元数为174 117)

表1 阴影光线遍历性能对比

场景算法遮挡光线非遮挡光线遍历时间(s)预计算时间(s)内存开销(M) 节点相交测试数/光线图元相交测试数/光线节点相交测试数/光线图元相交测试数/光线 Bedroom标准54.247.961.739.62.21–– SATO52.0 (–4.1%)41.0 (–14.4%)––2.020.19– SRDH44.0 (–18.8%)38.2 (–20.3%)58.0 (–6.0%)37.0 (–6.6%)1.931.4713.7 本文37.0 (–31.7%)32.1 (–33.0%)39.0 (–36.8%)–1.710.30(52%) Sponza标准32.627.348.841.82.09–– SATO39.0 (+19.5%)32.5 (+19.1%)––2.130.05– SRDH30.0 (–8%)23.0 (–15.8%)46.0 (–5.7%)40.0 (–4.3%)1.870.333.06 本文23.0 (–29.4%)19.0 (–30.4%)35.0 (–28.3.0%)–1.670.10(48%) Conference标准32.039.724.422.03.20–– SATO29.0 (–9.4%)36.7 (–7.6%)––3.070.17– SRDH30.0 (–6.3%)31.0 (–21.9%)24.0 (–1.6%)20.0 (–9.1%)2.821.136.89 本文24.0 (–25%)29.0 (–27%)17.0 (–30.3%)2.500.28(67%) FairyForest标准57.725.960.041.82.60–– SATO57.0 (–1.2%)24.7 (–4.6%)––2.420.12– SRDH49.0 (–14%)22.0 (–15.1%)55.0 (–8.3%)36.0 (–13.9%)2.160.746.99 本文47.0 (–18.5%)23.2 (–10.4%)41.0 (–31.7%)–2.210.32(105%)

为进一步分析中间图元的选择和索引位置的合理性，图3描述了中间图元的索引深度对遍历代价的影响。通常，越多的遮挡光线与在较高层次的中间图元相交，剔除的子树空间越大。对于大部分场景，光线终止遍历的深度位于树的中上层，即范围在10~19之间，与预期相符合，说明图元的选择机制是有效的。

(2) 本文算法对非遮挡光线遍历性能的影响，见表1。在节点相交测试数方面，SRDH算法降低了5.7%~8.3%，本文算法为28.3%~36.8%，具有更显著的降低率。尽管，SRDH算法重新划分了场景，对非遮挡光线，仅能够略微改变光线所经过的叶节点上的图元数，其对图元相交测试的影响并不大。而节点相交测试，SRDH算法依赖于自顶向下的遍历。本文算法通过邻接索引直接计算最近邻接点，剔除了大量自顶向下的搜索过程，减少了更多的子树相交测试开销。

图3 中间图元的索引深度对遍历代价的影响

本文利用帧间相关性预测光线的遮挡类型，以调用更适合的遍历算法。对部分非遮挡光线，不可避免的仍然使用的是标准自顶向下的遍历算法。而见表1中此类光线数目非常少，并不会对非遮挡光线的遍历性能提升有明显影响。此外，本文算法对场景Bedroom和Sponza提高了20%的遍历性能。

(3) 本文算法产生的预计算时间开销和内存开销，见表1，括号内值为相对于SRDH算法的内存开销减少量。在时间开销方面，本文算法远低于SRDH算法。尽管，相对于遍历时间，在预计算上减少的绝对时间并不明显。然而，目前的遍历算法是跟踪单根光线，若使用光束跟踪，遍历时间会进一步显著降低。此时，预计算时间在整帧绘制时间中占更高比例，降低预计算时间的作用更明显。相对于SATO算法，本文算法的预计算时间略高。但本文算法能同时提高2类光线的遍历效率，总体遍历性能明显优于SATO算法，并能够适应更多场景。因此，预计算时间的适当增加是能够接受的。在内存开销方面，以SRDH算法作为测试基准。由于仅存储可见区域底层节点的邻接索引，本文算法产生的开销仅是SRDH算法的48%~105%。

4 结 论

本文提出了一种基于多索引树的阴影光线遍历算法，通过增加图元索引和邻接索引，促使更多的遮挡光线在中间节点提前终止搜索；并减少非遮挡光线节点测试遍历代价。阴影光线的帧内相关性较强，利用SIMD指令进行光束跟踪，通常会获得比单根光线跟踪更好的性能提升。对于动态光源，可进一步挖掘树中节点关系，建立更灵活的访问关系来提高遍历效率。

[1] BENTLEY J L. Multidimensional binary search trees used for associative searching [J]. Communications of the ACM, 1975, 18(9): 509-517.

[2] RUBIN S M, WHITTED T. A 3-dimensional representation for fast rendering of complex scenes [J]. ACM SIGGRAPH Computer Graphics, 1980, 14(3): 110-116.

[3] IZE T, HANSEN C. RTSAH traversal order for occlusion rays [J]. Computer Graphics Forum, 2011, 30(2): 297-305.

[4] NAH J H, MANOCHA D. SATO: Surface area traversal order for shadow ray tracing [J]. Computer Graphics Forum, 2014, 33(6): 167-177.

[5] FELTMAN N, LEE M, FATAHALIAN K. SRDH: Specializing BVH construction and traversal order using representative shadow ray sets [C]//Proceedings of the 4th ACM SIGGRAPH/Eurographics conference on High-Performance Graphics. Goslar: Eurographics Association, 2012: 49-55.

[6] MACDONALD J D, BOOTH K S. Heuristics for ray tracing using space subdivision [J]. The Visual Computer, 1990, 6(3): 153-166.

[7] SHEVTSOV M, SOUPIKOV A, KAPUSTIN A. Highly parallel fast KD-tree construction for interactive ray tracing of dynamic scenes [J]. Computer Graphics Forum, 2007, 26(3): 395-404.

[8] CHOI B, KOMURAVELLI R, LU V, et al. Parallel SAH k-D tree construction [C]//Proceedings of the Conference on High Performance Graphics. Goslar: Eurographics Association, 2010: 77-86.

[9] PÉRARD-GAYOT A, KALOJANOV J, SLUSALLEK P. GPU ray tracing using irregular grids [J]. Computer Graphics Forum, 2017, 36(2): 477-486.

[10] 过洁, 徐晓旸, 潘金贵. 虚拟场景的一种快速优化Kd-Tree构造方法[J]. 电子学报, 2011, 39(8): 1811-1817.

[11] KENSLER A. Tree rotations for improving bounding volume hierarchies [C]//2008 IEEE Symposium on Interactive Ray Tracing. New York: IEEE Press, 2008: 73-76.

[12] BITTNER J, MEISTER D. T-SAH: Animation optimized bounding volume hierarchies [J]. Computer Graphics Forum, 2015, 34(2): 527-536.

[13] Foley T. KD-tree acceleration structures for a GPU raytracer [C]//Proceedings of the ACM SIGGRAPH/ Eurographics Conference on Graphics hardware. New York: ACM, 2005: 15-22.

[14] POPOV S, GÜNTHER J, SEIDEL H P, et al. Stackless KD-tree traversal for high performance GPU ray tracing [J]. Computer Graphics Forum, 2007, 26(3): 415-424.

[15] LAINE S. Restart trail for stackless BVH traversal [C]// HPG´10 Proceedings of the Conference on High Performance Graphics. Goslar: Eurographics Association, 2010: 107-111.

[16] CHOI B, CHANG B, IHM I. Improving memory space efficiency of kd-tree for real-time ray tracing [J]. Computer Graphics Forum, 2013, 32(7): 335-344.

A Shadow Ray Traversal Algorithm Based on Multiple-Index Tree

LIANG Xiao1, HUANG Yun2

(1. School of Computer Science, Southwest Petroleum University, Chengdu Sichuan 610500, China;2. School of Materials Science and Engineering, Southwest Petroleum University, Chengdu Sichuan 610500, China)

Shadow ray traversal is abig computation bottleneck in ray tracing. However, constructing an efficient tree to cull down redundant intersections is quite difficult. We propose a Multiple-index Tree based on shadow ray traversal algorithm, which adds indexes for nodes to accelerate traversal with acceptable pre-computation. First, since occluded rays try to intersect with primitive, we select primitives with high intersection probability from leaf nodes to store in inner nodes, which aims to stop traversal in upper tree. Second, since un-occluded rays try to find the nearest node, we create adjacency indexes between nodes in bottom tree, and use the indexes to access next node along ray direction directly. During traversal, by exploiting frame coherence, we estimate the occlusion type of rays and use corresponding method to reduce traversal cost. The experimental result suggest that the algorithm can improve traversal performance more than 20% for complex scenes. Even compared with tree reconstruction method, our method outperforms in reducing more intersections and only consumes 21% pre-computation time.

ray tracing; shadow ray traversal; hierarchy acceleration structure; branch decision

TP 391

10.11996/JG.j.2095-302X.2019030513

A

2095-302X(2019)03-0513-06

2018-11-15；

2018-12-02

西南石油大学启航计划项目(2015QHZ022)

梁 晓(1983-)，女，四川成都人，讲师，博士，硕士生导师。主要研究方向为计算机图形学、真实感绘制等。E-mail：xiaoliang.edu@foxmail.com