大型宽厚板轧机十字万向节疲劳寿命分析
2019-08-08戴照宝张尚斌王福胜汤达川樊昌杰
戴照宝 张尚斌 王福胜 汤达川 樊昌杰
(二重(德阳)重型装备有限公司,四川 618013)
现在绝大部分大型宽厚板轧机主传动系统都使用十字万向节,但由于其结构复杂,零件部分区域强度较弱,使其成为限制主传动系统使用寿命的瓶颈,而作为主传动系统的关键零件,其损坏必将引发生产事故,造成设备损坏、轧件报废等不可挽回的经济损失[1-4]。因为涉及到材料的疲劳使用寿命,国内很少有学者对此进行理论研究与实践验证。以国内某厂5 m轧机十字万向节为研究对象,在取得其材料基础性能参数的情况下,通过数值计算与软件模拟,得到其疲劳寿命,并与现场使用情况相对比,验证计算方法的有效性,以期对此类轧机的主传动系统使用寿命提供理论指导。
1 传动轴材料的特性参数曲线
1.1 材料应力应变循环特性曲线
结构的疲劳破坏是结构在循环载荷作用下的破坏,材料的循环加载特性是解决问题的关键。金属材料的应力-应变循环曲线方程为[5-6]:
(1)
式中,εt为总应变幅值;εe为弹性应变幅值;εp为塑性应变幅值;σa为应力幅值;E为弹性模量;K′为循环强度系数;n′ 为循环应变硬化指数。
根据Halford、Masing.Morrow假设,式(1)可修改为:
(2)
公式(2)实际上是应力应变滞回环的表达式,涉及金属材料在循环载荷作用下的循环硬化或循环软化特性。
某厂5 m轧机主传动接轴的法兰叉头、轴承压盖材料、十字轴材料、轴承外圈、辊子轴承材料、法兰叉头、轴承压盖把合螺栓材料的基础参数见表1,其材料变形抗力曲线如图1所示。
1.2 材料的应变疲劳寿命特性曲线
机械零部件的疲劳寿命均与其局部塑性应变循环有关。零件表面状态、局部几何形式、材料类型、载荷形式及大小均为影响塑性应变的因素,数据整理后的应变-寿命曲线通常被称为Basquin-Coffin-Manson曲线:
(3)
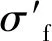
公式(3)可以表示为图2所示的曲线关系。
通过Jmatpro软件分别得到各相关材料的应变-寿命曲线,如图3所示。
2 材料疲劳寿命计算方法
2.1 材料应变寿命的平均应力修正

表1 接轴材料力学性能参数表Table 1 Mechanical property parameters of joint shaft material
(a)Cr2Ni2Mo(b)15CrNi4MoA(c)20Cr2Ni2MoA(d)34CrNi3Mo
图1 材料变形抗力曲线
Figure 1 Material deformation resistance curves
公式(3)是在等应变幅、零均值应变下的应变-寿命关系。一般认为零件在工作中所承受的循环载荷均存在应变和非零均值应力,故公式(3)不能系统地反映疲劳问题。根据试验研究,Morrow提出了新的修正方法,可提高应变-寿命关系式的精度:
(4)
式中,σm为各循环均值应力;εm为各循环均值应变。试验认为,均值应变对寿命影响很小,可将上式简化为:
(5)
Smith、Waston、Topper进一步提出了Smith-Watson-Topper(SWT)平均应力修正方法,其公式为:
(6)
式中,σmax为各完整循环的最大应力值;εa为单次循环的应变幅值。公式(6)由于反应了总应变-寿命关系,可更为精确地预估寿命。
2.2 Neuber修正法的局部应力应变法寿命估算
Neuber修正法可以将基于弹性应力的有限元分析结果转化为弹塑性应力应变,然后使用局部应力应变法进行寿命计算。
修正Neuber公式为:
ΔσΔε=(KfΔS)2/E
(7)
式中,Δσ为局部应力范围;Δε为局部应变范围;ΔS为名义应力范围;Kf为有效应力集中系数或疲劳缺口系数;E为弹性模量。Neuber缺口局部塑性修正方法如图4所示。
完整的应力应变循环是产生疲劳损伤的主要原因。当损伤积累到一定程度后,由Minner线形损伤积累法则可知,材料将出现工程可见裂纹:
(8)
式中,Nf,i为在某个恒定应变和应力均值循环条件下,通过试件的疲劳测试,直到破坏时所历经的循环数;ni为该恒定应力-应变均值在零件局部位置的实际载荷中出现的循环次数。
假定一个载荷块的疲劳损伤为:
(9)
其中零部件达到破坏的寿命为T=1/d。T为参与疲劳分析的载荷历程的块数。

(a)Cr2Ni2Mo(b)15CrNi4MoA(c)20Cr2Ni2MoA(d)34CrNi3Mo
图3 材料应变寿命曲线
Figure 3 Strain life curves of material
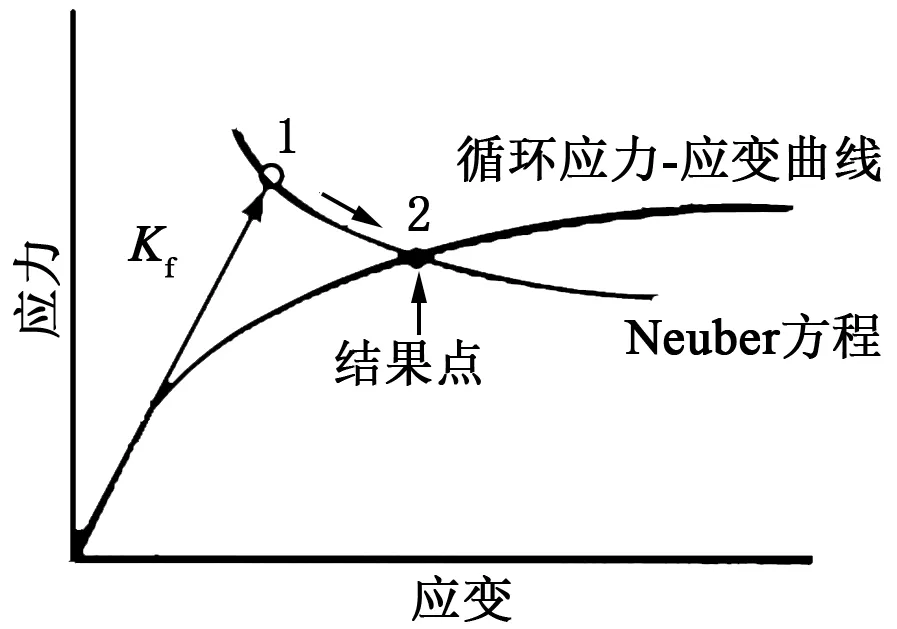
图4 Neuber缺口局部塑性修正方法Figure 4 Neuber gap local plasticity modification

持续时间s上接轴扭矩峰值kN·m下接轴扭矩峰值kN·m1234567891011121314151630030030030030030030030030030030030030030030030049054649441745395491423042754576434044244655410248924892462142275774567755525550478054295400538953745371534853165309529852805262
3 十字万向节疲劳寿命计算
3.1 疲劳载荷作用历程
某厂5 m轧机十字轴在工作过程中的扭矩测试值(绝对值)见表2,共16个记录,每次记录的时间历程均为300 s,从表中可以看到下接轴所受到的扭矩要大于上接轴所受扭矩。为保守起见,取作用在下接轴上的扭矩来进行疲劳分析。
图5记录的是5 m轧机上午1点开始的300 s内下接轴所受到的扭矩曲线图,其最大扭矩绝对值为5774 kN·m。在疲劳计算中,以300 s扭矩时间历程为一个循环周期,进行疲劳分析,计算十字轴结构能够承受多少个这样周期的载荷。

图5 下接轴所受到的扭矩曲线图Figure 5 Torsion curve of bottom joint shaft

图6 传动轴力矩提取图Figure 6 Moment selection of transmission shaft
图5所示的扭矩曲线图输入FE-Fatigue,经雨流计数后,载荷的时间历程直方图如图6,图6中纵坐标放大5800倍后即为下接轴所受到的实际扭矩值,因有限元计算中的分析工况扭矩取5800 kN·m,因此在图6中缩小5800倍。
3.2 计算结果
从图7(a)和(b)可看出,十字轴最严重部位的疲劳寿命为6.88×104次循环,由于每次循环为300 s,因此十字轴的疲劳寿命为5733.3 h,即238.9天。
(a)疲劳寿命图 (b)损伤等值线 (c)局部应变雨流计数循环直方图 (d)损伤直方图
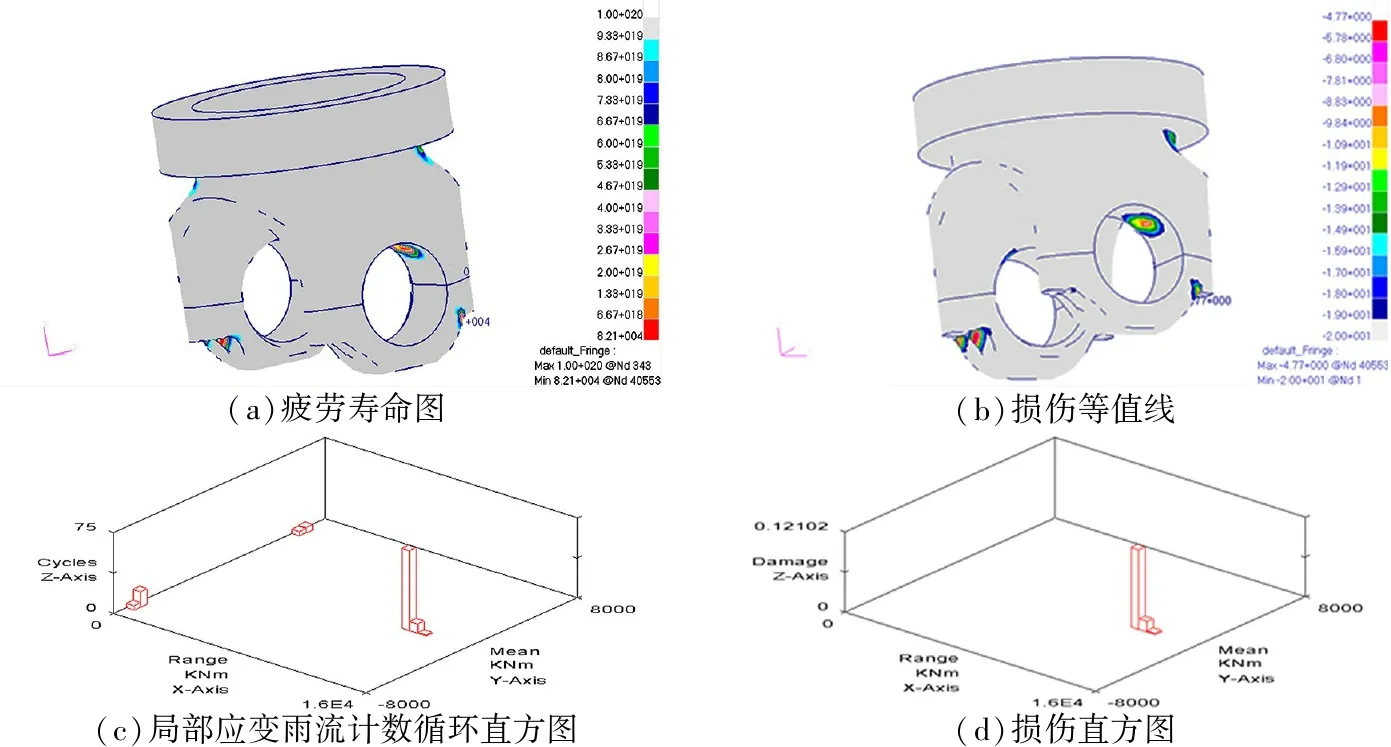
图7 十字轴Figure 7 Cross axle

图8 叉头压盖Figure 8 Jaw gland
图9 螺栓
Figure 9 Bolt
从图8(a)和(b)可看出,叉头压盖最严重部位的疲劳寿命为8.21×104次循环,由于每次循环为300 s,因此叉头压盖的疲劳寿命为6841.7 h,即285.1天。
从图9(a)和(b)可以看到,螺栓最严重部位的疲劳寿命为5.6×105次循环,由于每次循环为300 s,因此螺栓的疲劳寿命为46666.7 h,即1944.4天。
从图7(c)和(d)、图8(c)和(d)和图9(c)和(d)可以看出,大扭矩载荷作用次数虽然在数量上远少于小扭矩载荷的作用次数,但却是造成疲劳破坏的主要原因。

表3 主传动轴各处材料的坯料寿命分析结果Table 3 Life analysis results of various material blank for main transmission shaft
在有限元计算中,滚子轴承简化为一个等效圆管来替代,此处的疲劳分析也只能是借助于有限元的分析结果来进行,通过分析发现轴承外圈和滚子轴承具有无限寿命,因此不再给出寿命等值线图。
4 结论
通过疲劳寿命分析,得到某厂5 m轧机主传动接轴各处材料的使用寿命结果,如表3所示。
按上述平均载荷作用后的使用寿命最低为238.9天,与现场实际使用情况相似,证明此分析过程是有效的,此方法可作为此类轧机主传动疲劳使用理论计算的辅助工具。
