基于安全屏障监控的车道自动保持控制*
2019-08-08陈亚伟邵毅明束海波郝西祥
陈亚伟,邵毅明,束海波,郝西祥
(1.重庆交通大学机电与车辆工程学院,重庆 400074; 2.重庆交通大学交通运输学院,重庆 400074)
前言
车道保持控制作为一种驾驶辅助系统,可以使车辆保持在规定车道内行驶,提高驾驶舒适性和安全性。它是车辆运动控制的关键技术之一,直接影响车辆的行驶安全性[1-3]。
近年来,针对车道保持控制的研究日益增多。文献[4]中通过仿真比较了H∞、自适应PID和模糊控制在车道保持方面的性能。文献[5]中提出了PID自动转向控制,并通过轨迹仿真验证了有效性。文献[6]中同时设计了多个稳定控制器,以防止传感器故障,实现容错车道保持。文献[7]中为提高跟踪精度和平顺性,提出了一种频率整形预览控制算法。综上所述,车道保持控制研究日益得到重视,但如何基于车辆的动力学特性,在保证平稳转向的同时,确保行车安全,实现安全与车道保持的协同控制,还有待进一步讨论。
虽然通过滤波和降低增益等方法可实现平稳运行,但是此类方法可能会降低跟踪精度和安全性,尤其是在弯道行驶时,这种现象更加明显。车道保持的安全性涉及到车道偏离、周围车辆干扰和车道检测失败导致的不稳定性等多方面因素。在本文中,设定安全行驶的关键指标是保持小的横向偏移和航向角误差,以避免车道偏离。
如图1所示,不同于对平滑性考虑,安全性是高度非线性的。如果跟踪误差很小,显然车辆的转向平滑度更重要,但随着误差的增加,安全则变成首要考虑因素。
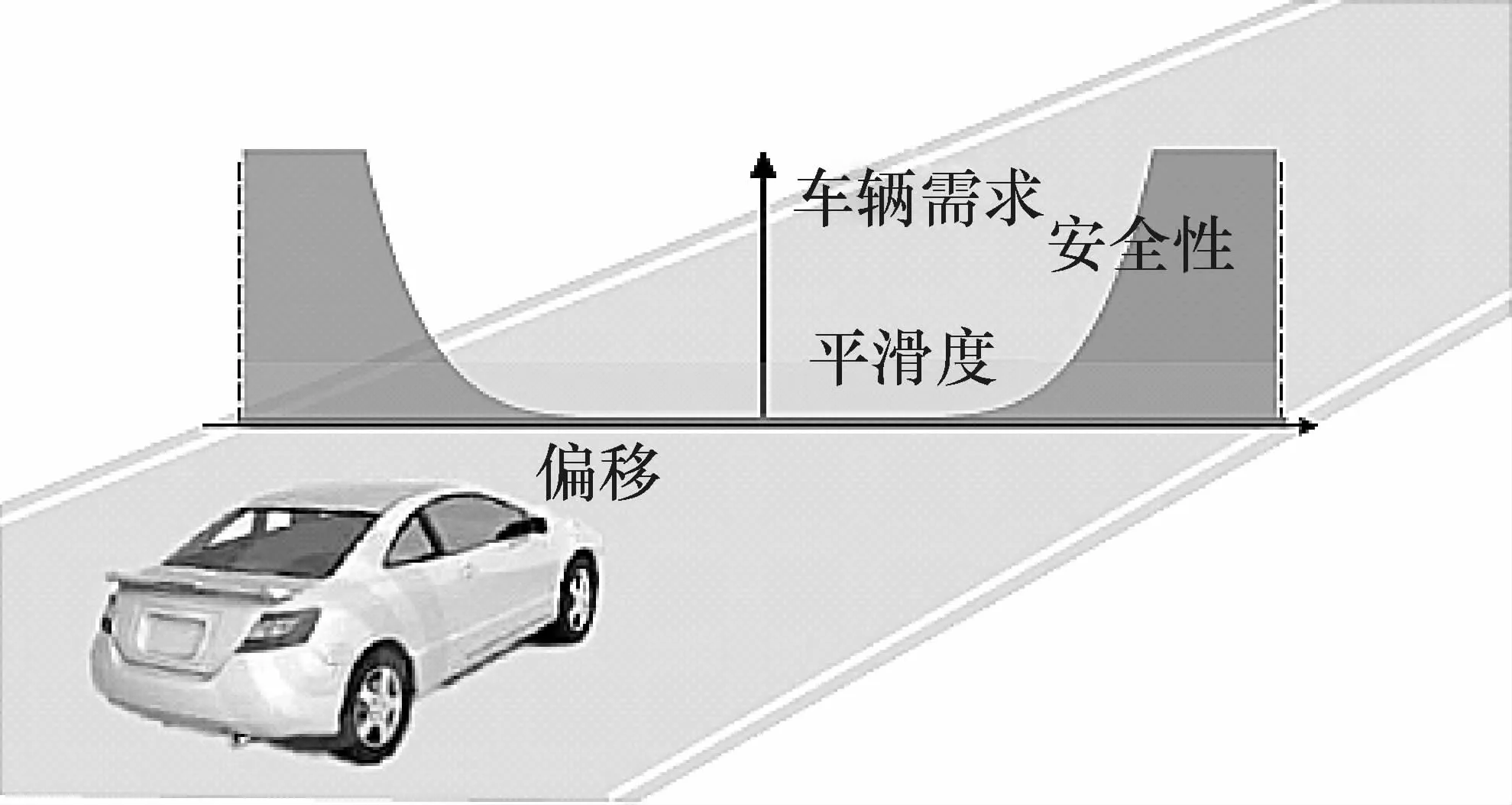
图1 平滑性与安全性分析
基于上述分析,本文中以车道保持控制为研究对象,在分析其结构与特性的基础上,提出了一种安全监控的预览车道保持控制算法。具体来说,主要完成以下工作。
(1)为实现平滑的车道跟踪,提出了一种离散时间预览控制算法,该算法与Mobileye模块协同工作。
(2)为保证安全,设计了一种基于屏障功能的控制方法,与预览控制并行工作。其主要特点是可防止车辆离开安全区,但如果汽车是安全的,则保持休眠状态。
(3)在实车上加载控制算法,进行仿真和道路测试,以验证该控制算法的有效性。
1 车道保持系统模型
在本节中,建立了车道模型和车辆横向动力学模型,提出了最优车道保持问题的代价函数。
1.1 车道模型
本文中使用一个Mobileye 660模块来感知车道标记,该视觉系统输出涉及到的每个车道标线的详细信息,包括横向偏移量、航向角误差、车道曲率及其导数、车道检测质量、最大感知范围和车道标线类型。车辆局部坐标系下的车道轮廓线由3阶多项式描述,即
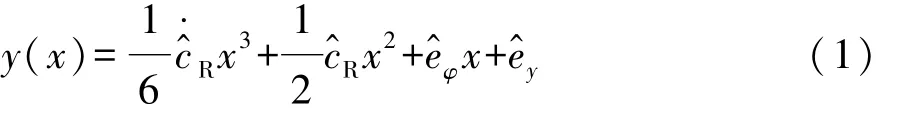
式中 x为纵向距离,x∈ [0 ,x^max]。将上述多项式记为
前方道路曲率为

由于传感器安装在前风窗玻璃上,在车辆质心之前ds处,因此测得的e^y被修正为

由于ds的影响较小(大约0.4 m),在其它观测结果中便不再进行修正。
基于车道标记生成参考路径Ω,实现车辆的实时导航。如果只检测到车道标线的一侧,则参考路径Ω为

式中d0为车道标线到车辆质心的期望偏移量。
如果检测到两边车道标线,则设定参考路径Ω为
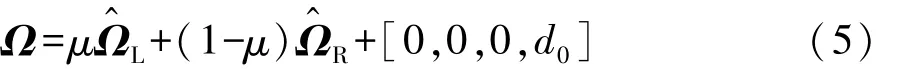
1.2 车辆横向动力学模型
采用车辆单轨动力学模型进行控制设计,图2为车辆横向动力学示意图,表1为图2中符号及其含义。本文中假设车辆不失稳定性,即侧向加速度小于0.3g,因此,可认为轮胎的侧向力与其滑移角成正比[8]。
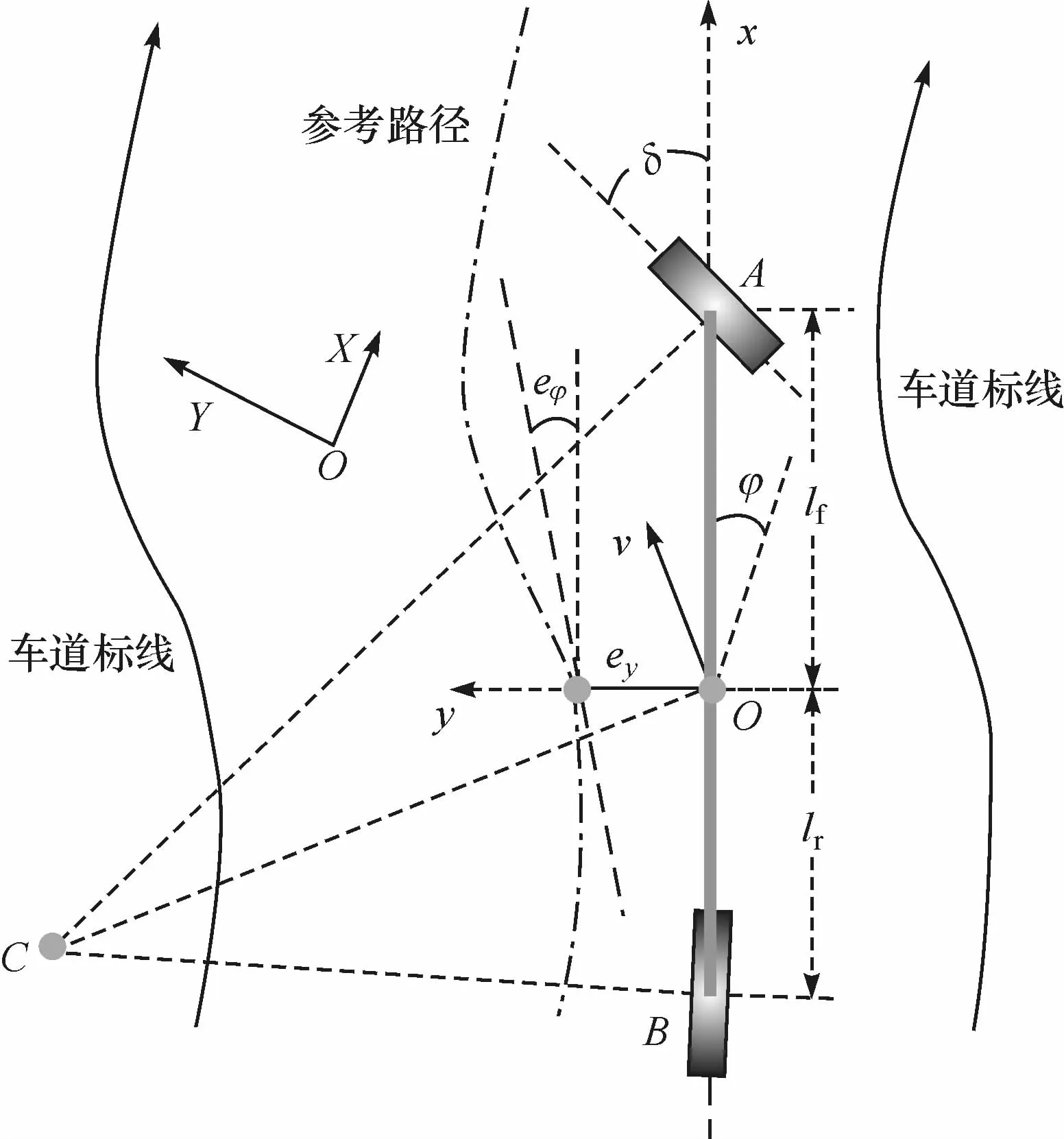
图2 车道保持控制的车辆动力学模型

表1 动力学模型的符号及定义

其中:
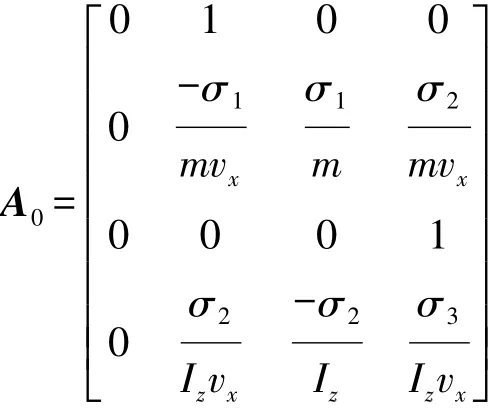
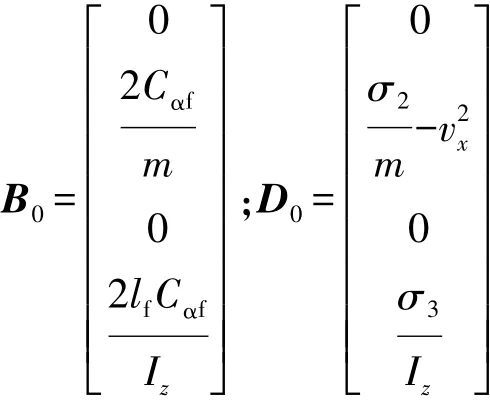
式中σi为集总系数,定义为
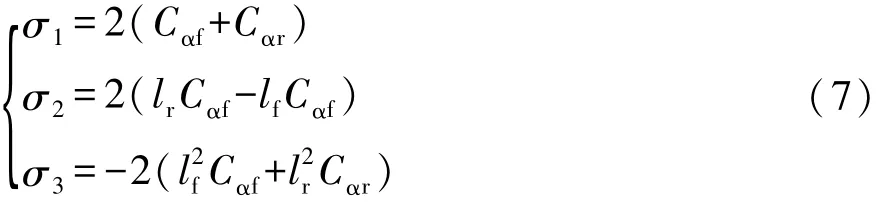
控制输入为前轮转角δ,δ∈R R,车道曲率cR为关键扰动,cR∈R R。为便于控制器的设计和实现,将连续时间系统式(6)转换为具有固定采样周期Δτ的线性离散时间系统,表示如下:
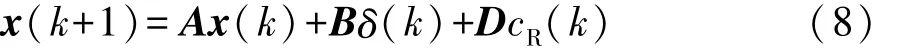
式中:A∈R R4×4;B∈R R4;D∈R R4;k为阶跃序列。
1.3 最优车道保持
将车道保持任务转换为最优控制问题(OCP),该问题要求具有最小化的平滑性和面向精度的代价函数,该函数为
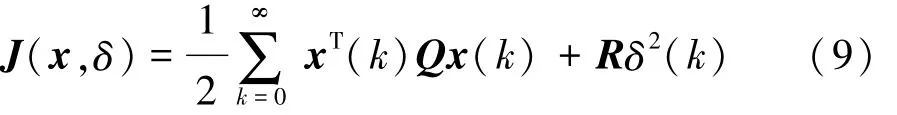
式中Q∈R R4×4和R∈R R分别为半正定阵和正定矩阵,即 Q≥0,R>0。
式(9)需在无界范围内获得 cR的数值,由于Mobileye的最大范围约为100 m,因此在时刻k,cR仅在窗口[k,k+N]中可用,其中N是预览步数。假设预览窗口之外的道路是直的,即
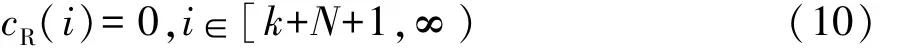
虽然通过减小跟踪误差x(k)可对代价函数进行调整,但随着误差的增加,安全准则变得更加重要,因此,需要对 ey和 eφ施加一个硬约束Φ,即

2 预览车道保持控制算法的设计
本节中首先设计预览控制算法而不考虑安全约束式(11),然后在第3节中设计屏障控制算法。当式(8)中的扰动D·cR(k)为0时,车道保持系统式(8)~式(9)成为一个线性二次调节器(LQR),从而可以解析求解,但D·cR不为0。针对这种时变扰动,一种直接的方法是在线数值求解优化问题,但在线计算时间长,实时性较差[10]。与耗时的数值方法不同,本文中提出的预览控制方法通过在状态向量中加入未来扰动来寻求解析解,然后将其作为一个增广的LQR问题进行求解[11]。
为消除扰动,将[k,k+N]中的 cR(k)和原始系统状态 x(k)合并为增广状态矩阵 χ(k):
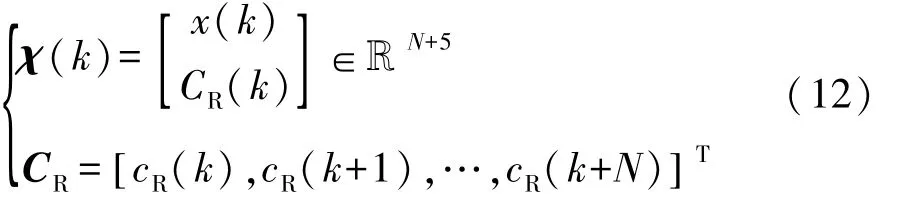
代价函数变为如下所示:
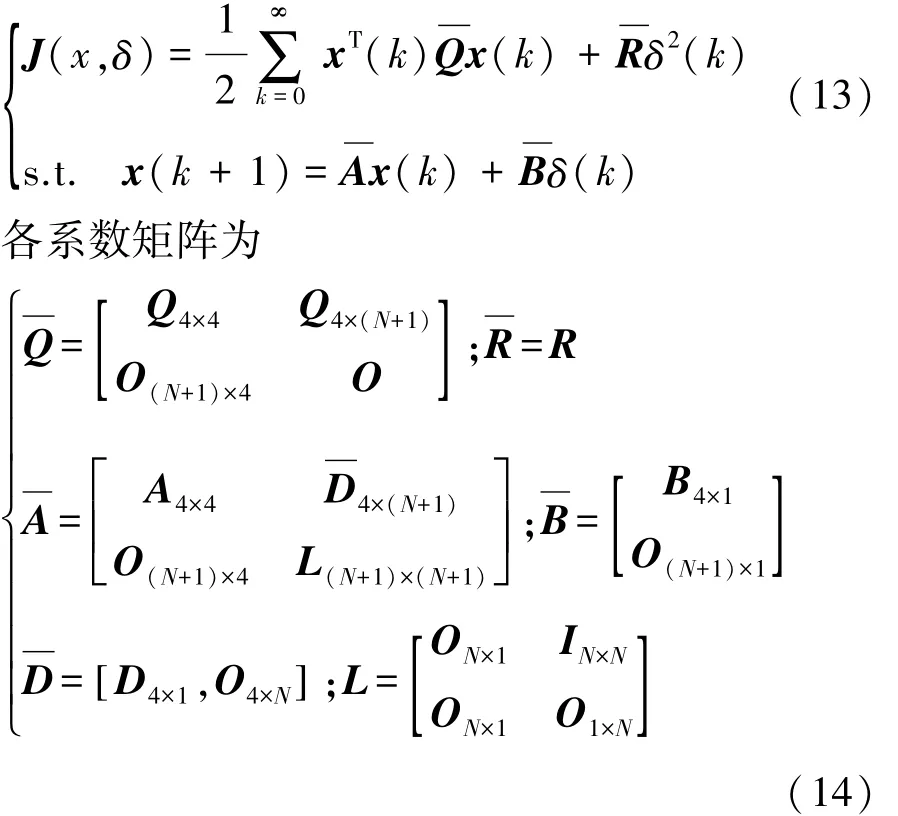
式中:O和 I为0和单位矩阵;L为预览曲率的映射。
对于该增广时不变的LQR问题,可以通过Pontryagin的最大(或最小)原则来求解:
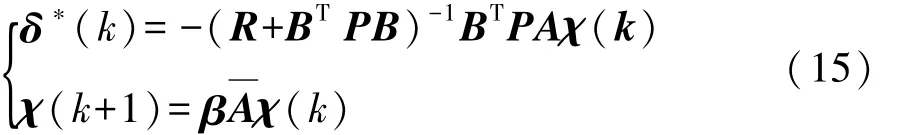
式中 β=βT=(I+B R-1BTP)-1为集总矩阵。P由黎卡提方程解出:

为避免求解高维方程式(16)和对 x(k)与CR(k)解耦,将 P分为4个子矩阵并简化式(16)的运算:
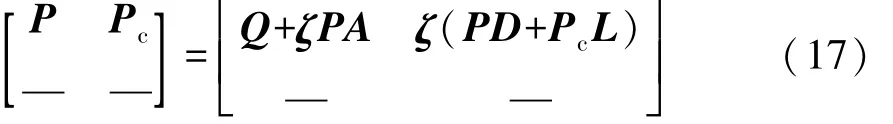
其中 ζ=AT(I+PB R-1BT)-1
由式(17),求出矩阵 P和Pc:

式(18)的第1个方程实际上是没有预览模块的原始系统的黎卡提方程。由于式(14)中D 和L的特殊结构,因此,求解式(18)的第2个方程:
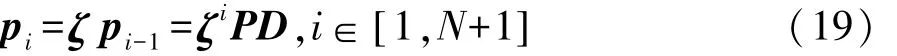
式中pi为Pc的第i列向量。
将式(18)和式(19)代入式(15)得到最优控制:
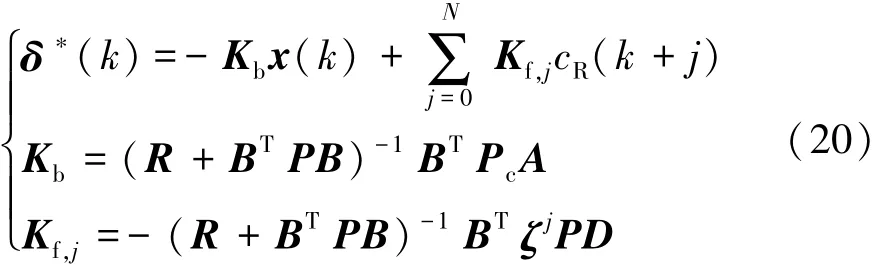
式中Kb∈ RR和Kf∈ RRN+1是反馈增益向量。
将δ*代入式(13),可得
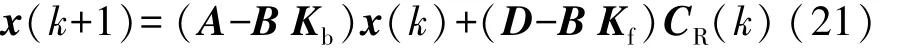
最优控制式(20)由两部分组成:第一部分Kbx(k)是反馈响应,通过Q和R可减少增益Kb以获得更平稳的转向;第二部分KfCR处理预览的车道曲率,并基于未来车道曲率和车辆动力学生成主动转向。前馈控制是一种较好的前馈控制方式,在扰动到达车辆之前进行动作,是实现更平稳、更准确控制的关键。
由车道标线模型式(1)和式(2)可知,车道曲率为线性变化,预览控制可简化为
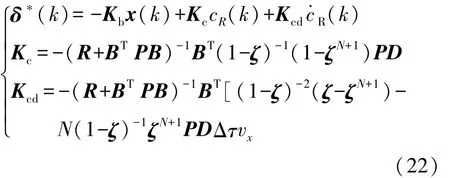
如果N足够高,则Kc和Kcd收敛于
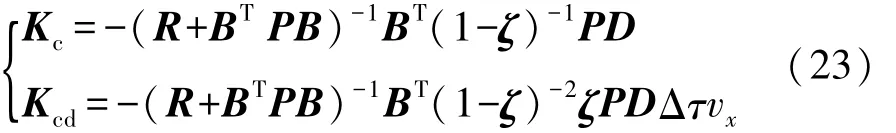
由式(22)可知,控制器仅包含 x(k),cR(k)和)的反馈操作。也就是说,控制器只需6个增益,并且定时性较好。
如果去掉预览部分,控制器则成为简单的比例微分(PD)控制:
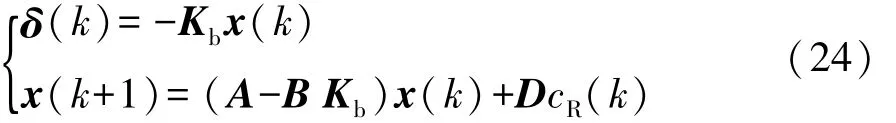
3 安全屏障控制设计
为满足安全约束式(11),设计了一个安全屏障,并将其施加到所提出的预览控制上[12]。
为限制车辆使其处于安全区,引入以下不等式约束:
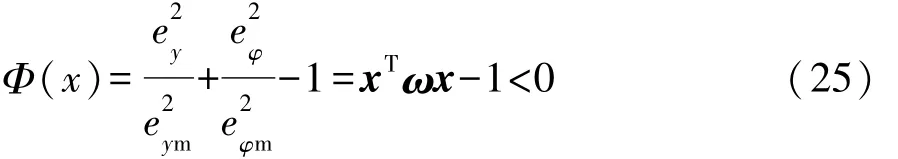
式(25)将安全区定义为一个椭圆区域,用ψ={ x Φ<0}表示,边界为 ψ={ x Φ=0}。
利用屏障控制使x∈ψ,安全屏障函数设计为

上式具有特殊的性质,即当x→ψ时,h→0,表示边界上的能量为0;当x→0,h→1,表示能量最高和安全行驶。如果x趋近于ψ,可以阻止h的减小,那么系统就会保持在h>0的ψ内部。该过程可通过限制·h的大小来实现。

式中:γ>0;ε为松弛因子,用于稳定系统、补偿系统延迟和模型不匹配。
由式(27)的约束,当x远离ψ时,h可以自由改变,当 xp→ψ,·h→0时,h将停止增加。
根据采样时间Δτ,式(27)可以变换为
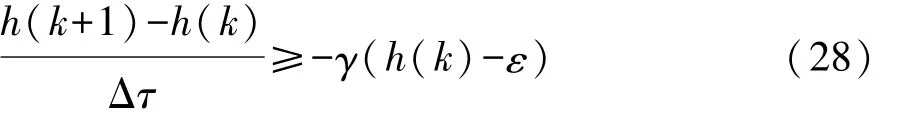
h(k+1)由以下泰勒级数近似得到:
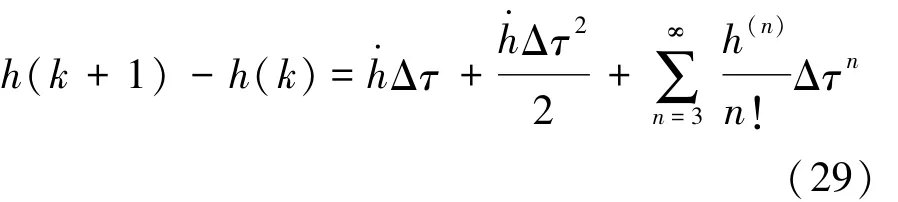
对h求导得到如下结果:
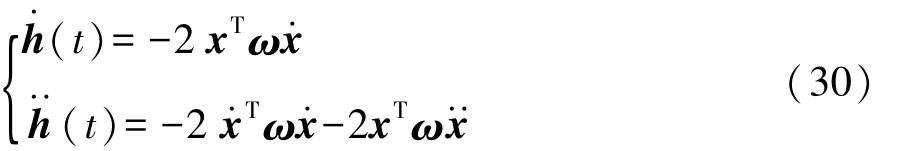
为简化以下表示,定义一个新的矩阵ωe为
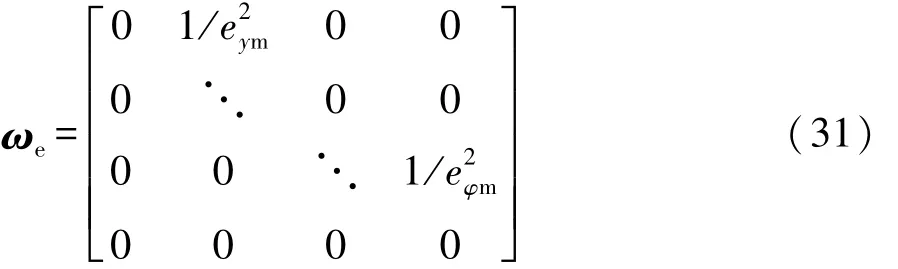
状态变量x及其导数满足以下的关系:

将式(6)、式(29)和式(32)代入式(28),得到保证x∈ψ的输入δ为
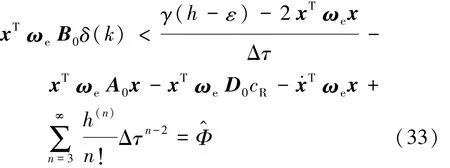
在线应用中,可以忽略泰勒展开的高阶近似。式(33)生成了面向安全δ的可行集合,当车辆接近屏障ψ时,该可行集合主动干涉预览控制过程。
在式(33)中δ的边界为

通过安全屏障控制δ,预览控制δ*监督生成最终的转向指令δ*为
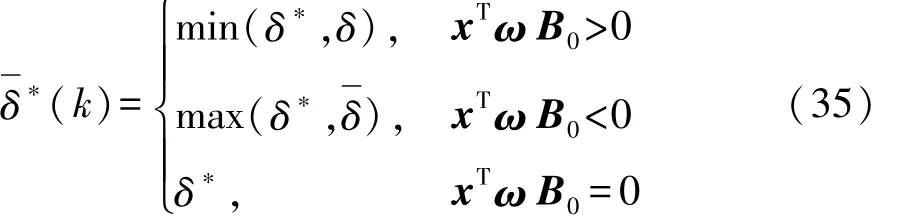
其中,如果xTωB0→0,δ→∞,则δ*=δ*。
4 实车实验
将所提出的安全监控预览车道自动保持算法载入到实际车辆,然后在实际道路进行实验,验证所提算法的有效性。
4.1 车辆平台及算法实现
如图3所示,用于道路实验的车辆为吉利博瑞,配置的Mobileye 660和IMU模块可测量横向跟踪误差、横摆运动和未来道路曲率。

图3 实验测试车辆
采用C++语言实现由安全屏障功能监控的预览车道保持控制,车辆动力学参数如表2所示。
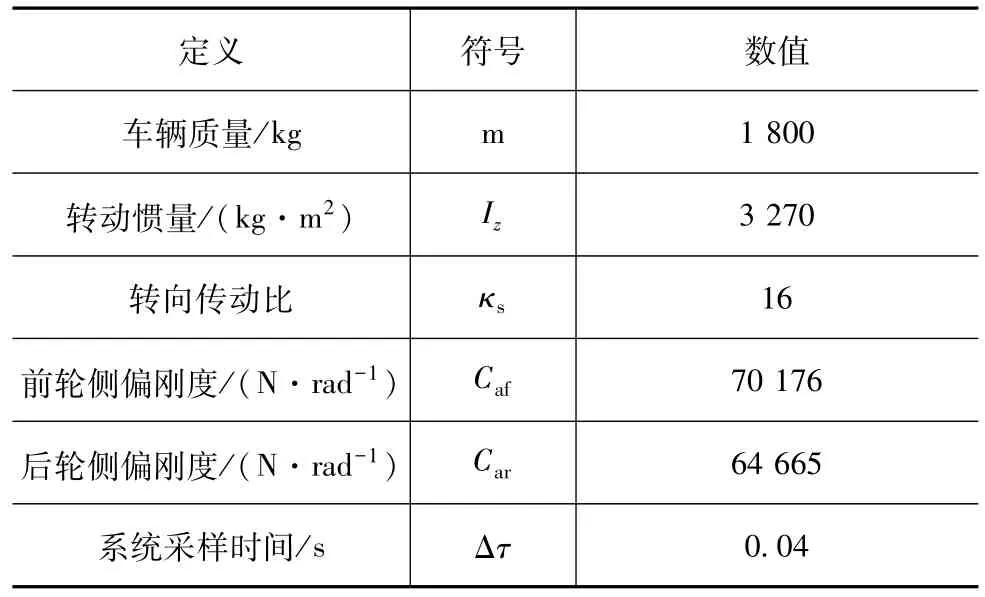
表2 车辆参数
4.2 仿真分析
为减少模型不匹配,使用单轨模型式(6)来估计车辆动力学。如图4(a)所示,道路由直线部分和随后半径为200 m的曲线组成,车速设定为20 m/s。具有安全屏障功能的预览控制和PD控制结果如图4所示。
(1)预览控制的性能
将预览控制与PD控制进行比较,预览控制在车辆进入曲线之前就开始发挥作用,PD控制器仅在进入车辆曲线后才发挥作用,并且在转向和横向位移中出现超调现象。
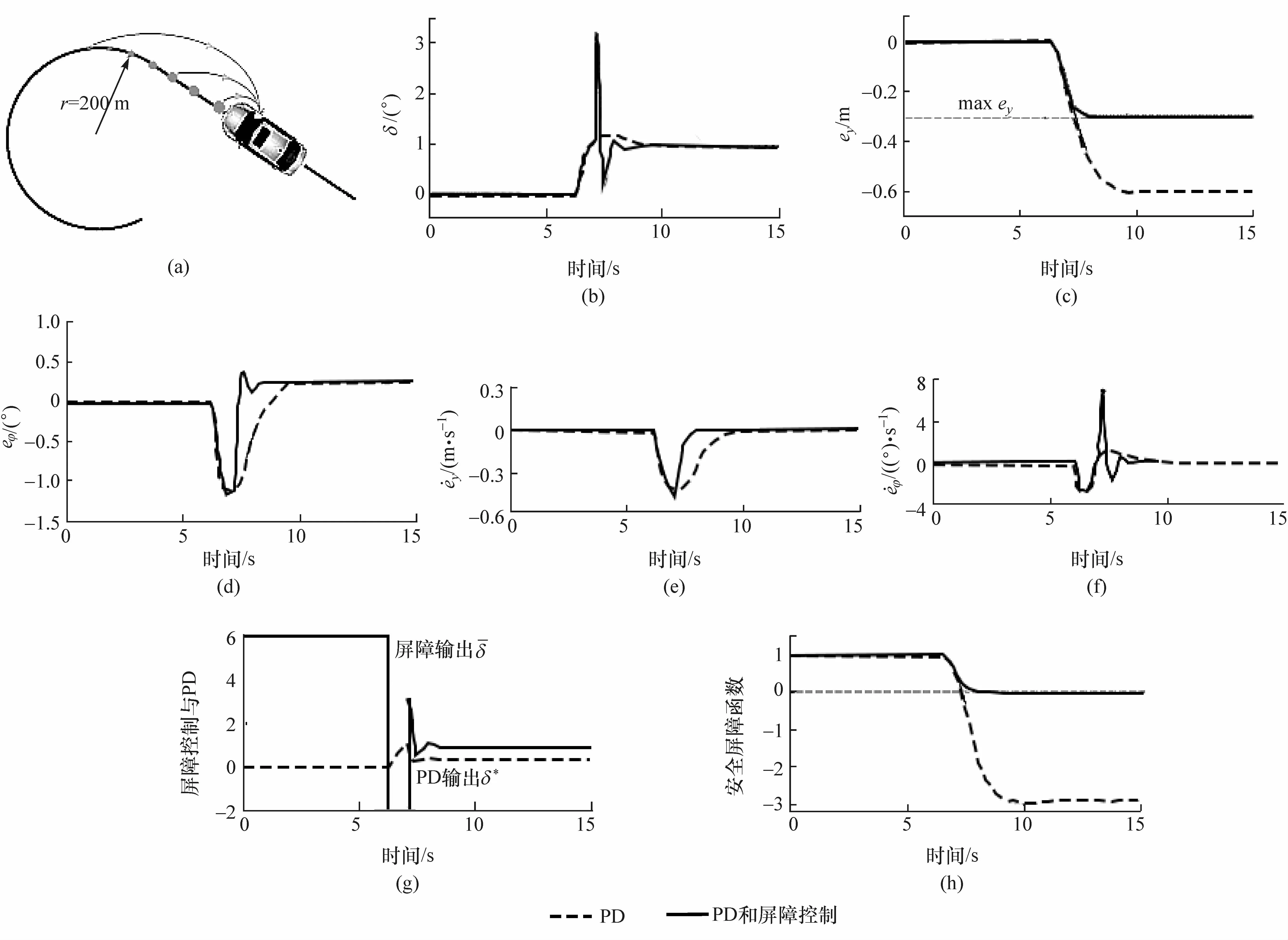
图4 安全屏障监控的预览控制仿真结果
如图4(c)所示,预览控制的横向偏移ey进入稳态为30 cm,PD控制下的横向偏移ey最大值为60 cm。可看出预览控制可以减小控制误差,提高车辆的安全性。
(2)安全屏障控制的性能
设置 γ=4,eym=30 cm,eφm=15°以激活屏障控制。由于预览控件的误差较小,在这种情况下其屏障控制不会调整其动作。在PD控制中横向偏移ey的最大值为60 cm,这已经超出了式(25)给定的安全约束。
在图4(h)中,PD控制下的屏障控制函数h(x)在t=7 s时已经变为负数;而屏障控制器使前轮转角向左转2°,这可以防止h(x)下降到0。由PD控制和屏障控制计算的δ的数值如图4(g)所示。
由上述仿真结果可知,屏障控制的主要优点:在车道保持控制是安全的情况下不发生动作,一旦车辆接近安全边界便立即启动进行转向控制干预。
虽然仿真中预览控制实现了精确的车道保持,但是由于模型的不确定性、外界干扰和感知误差,仍然需要屏障函数。
4.3 实验结果
如图5所示,在实际道路上,对提出的基于安全屏障监控的预览车道保持控制算法进行了测试,实验道路存在高度弯曲的路段,最小半径约为75 m。其中,图5(a)为实验路线卫星图,图5(b)和图5(c)为道路测试场景,图5(d)为所开发的软件界面。

图5 路测场景
(1)预览控制的性能
道路测试实验结果如图6所示。从图6(a)可知,道路曲率及其导数与真实道路轨迹大致吻合。在最初的105 s内,车辆以32 km/h的速度行驶,经过十字路口后,以50 km/h的速度巡航行驶。实验过程中,车辆的速度会自动适应道路曲率,以避免高横向加速度,如图6(c)所示,在140 s时,速度会下降到30 km/h。
如图6(b)所示,转向盘转角在±10°范围内波动,但在最剧烈的转弯时,转向盘转角κsδ高达30°,图中的阴影区域代表与道路曲率相关的预览控制,它对转向角的控制超过70%,其余部分来自与跟踪误差相关的反馈控制。
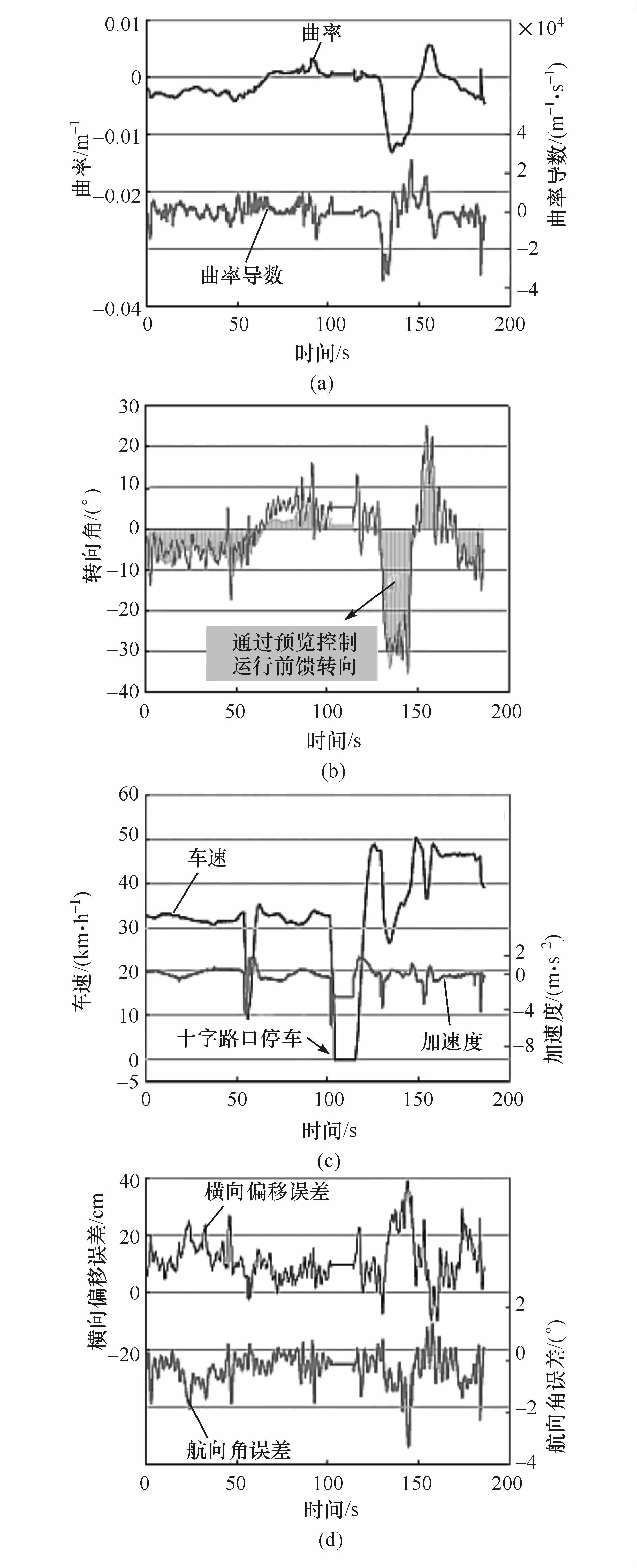
图6 道路车道保持实验结果
如图 6(d)所示,ey/eφ的最大值为 40 cm/3.5°,发生在道路曲线最尖锐的地方。
(2)安全屏障控制的性能
安全屏障控制的实验结果如图7所示,实验最大车速约为60 km/h,最小路面半径约为10 m。在转弯段,车道标记不可用,使用实时动态(RTK)定位系统来提供虚拟车道。
在PD控制下,横向偏移ey的峰值为42 cm。采用屏障控制来干预PD控制并设置安全误差界限为eym=30 cm。如图7所示,误差限制在30 cm以下,并且安全屏障函数h(x)>0。从图7中可以看到,横向误差在边界内被限制,从而在一定范围内输出。
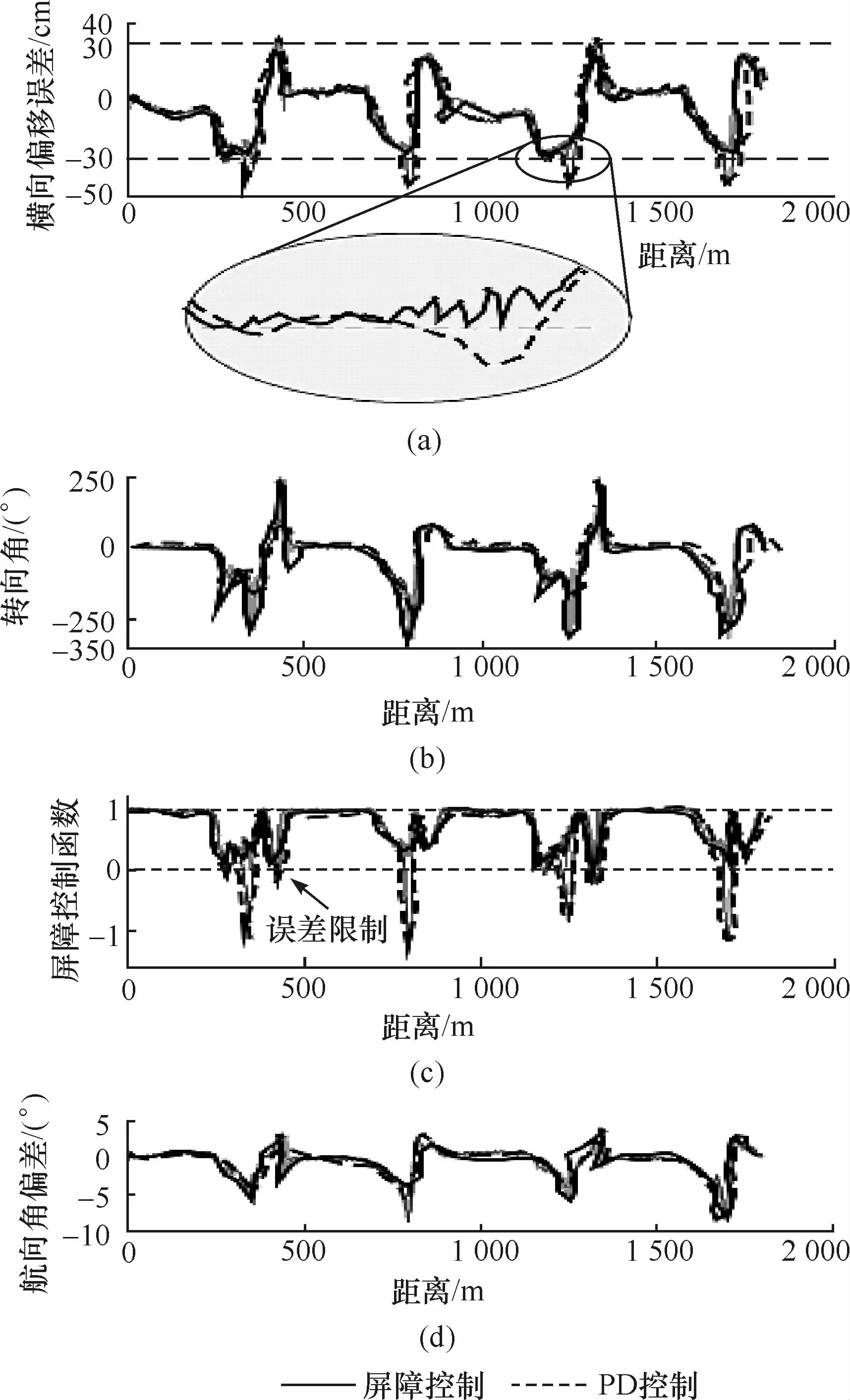
图7 安全屏障控制实验结果
5 结论
本文中提出了一种安全监控的车道自动保持控制算法,实现了车辆的安全和车道保持的协同控制。通过仿真和道路实验,验证了控制系统的性能,得出如下结论。
(1)基于最优控制理论设计的预览车道保持控制算法,可使车道形状变化的响应更加平滑,而且在弯道上具有较高的跟踪精度。
(2)为保证车道保持的安全性,提出了安全屏障算法来监控预览车道保持控制器。该安全屏障控制仅在车辆即将离开安全区时启动工作,其余时间保持休眠状态。仿真和实验结果表明,车道保持精度高,跟踪误差有界,并且安全可靠。
