P2P网络借贷利率的非线性特征及预测研究

侯慧敏 刘峰涛

摘要：P2P网络借贷作为互联网金融中的重要组成部，在推进利率市场化和小微金融的发展中扮演者重要角色。P2P网络借贷市场已被众多学者证明为是一个非线性复杂系统，而反应其市场价格的P2P借贷利率也呈现出非线性特征，这使得对其波动特征的把握以及未来趋势的预测具有重要现实意义。本文简要介绍了P2P网络借贷利率的非线性特征，并据此对P2P网络借贷利率未来趋势进行预测。

关键词：P2P网络借贷利率  非线性特征  趋势预测

一、引言

与国外P2P市场相比，国内的P2P网贷行业内部发展参差不齐，人们认为P2P网贷平台利率于高、风险大，可能面临平台倒闭的风险。P2P网贷市场中博弈关系众多、变量要素多，使其呈现复杂性特征，并以非线性方式与外界进行信息交换。P2P网贷利率的波动会对投资者收益、借款人融资成本以及平台稳健运营产生重要影响。所以从利率端着手正确分析P2P网络借贷利率的波动特点、准确地预测其走势变化，对于监管当局、平台、投融资具有重要的现实意义。

二、P2P网络借贷利率的非线性特征分析

非线性通常是相对于线性而言，具备线性特征需要满足以下条件：一是符合叠加原理，二是变量间的关系是直线关系。非线性则不遵循叠加原理，且非线性关系中变量是相互作用的。P2P网贷利率具有以下非线性特征：

（一）P2P网贷利率的非线性依赖结构

检验序列是否存在非线性依赖结构的常用办法是BDS统计检验。国内徐欢基于BDS统计检验，对包括P2P网络借贷利率在内的四个时间序列进行非线性依赖结构检验，其研究结果表明，四列指数的时间序列对数增长率均具有显著的非线性依赖结构，推测出P2P网贷序列的非线性依赖结构可能源自于低纬混沌过程。

（二）P2P网贷利率的非正态性

传统金融理论认为金融资产收益率遵循随机游走，其概率分布接近于正态分布或对数正态分布。但现实中大量实证表明，市场中的资产收益率并不呈现正态分布。P2P网贷市场非正太性特征研究方面，国内学者已研究证明P2P网贷利率序列分布并不是正态分布，而是呈现右偏、尾部比正太分布尾部薄的“矮胖”形状。

（三）P2P网贷利率波动聚集性

P2P网络借贷综合利率的波动聚集性是指，一段时间内利率在出现较大幅度波动后会紧接着出现另一较大幅度波动，或在出现小幅度波动后紧跟着另一小幅度波动。P2P网贷利率的波动聚集性特征研究方面，国内学者何启志采用AR-GARCH模型检验序列的波动聚集性特征，证明了P2P网贷市场利率的波动具有显著的波动聚集性。

三、 P2P网络借贷利率的趋势预测

对于具有非线性特征的P2P网络借贷利率进行趋势预测，传统的基于线性范式的经济学方法显然不能满足非线性分析的要求，且单一模型和简单组合预测模型不能满足分析要求，本文采用多尺度组合预测模型，对P2P网贷利率序列进行分析和预测。本文的多尺度组合预测方法基于分解—重构—集成的思路，首先采用经验模态分解法（EMD）将原始序列进行分解得到若干本征模态（IMF）和一个残差项;然后采用均值重构法将各IMF重构为不同频率的分量;最后根据不同分量的波动特征采用不同的预测方法，并将各个预测分量的加总最为最后的预测结果。

（一）EMD模型算法

EMD方法的分解过程可以将各IMF和残差项逐一分解出来，从高频到低频依次排列。设原始序列为Y（t），EMD模型算法具体步骤如下：

第一，对于原始序列Y（t），确定所有局部极大值点与极小值点。

第二，用三次样条插值法分别拟合出由极大值点和极小值点分别确定的上包络线和下包络线Emax（t）、Emin（t）。

第三，计算上下包络线的均值M（t）=Emax（t）+Emin（t）。

第四，原始序列Y（t）减去M（t），得到两者差值D（t）=Y（t）-D（t）。

第五，若D（t）满足IMF的定义，记D（t）为第j个IMF，序列为Cj（t），记残差R（t）=Y（t）-D（t），将R（t）作为新的原始序列Y（t）;若D（t）不满足IMF的定义，将D（t）作为新的原始序列Y（t）。

第六，重复以上步骤，直到从Y（t）中分解不出新的IMF，此时序列Y（t）通常是常函数或者单调函数。

（二）均值重构算法

在实际应用中我们只需分析相似性较高的IMF分量组，而不用对每一个IMF分量都进行详细分析，一方面可以减少工作量，一方面IMF分量组合比单个IMF更具实际意义。因此可采用从粗到细的均值重构算法（fine- to-coarse reconstruction）对原始序列进行模态划分，并赋予其经济含义。均值重构算法具体步骤如下：

第一，计算从IMF1到IMFm的和序列的均值。

第二，选取显著水平α，利用t检验判断Sm均值中从哪一个m起，该均值显著偏离0，一旦m被识别为转折点，则将IMF1到IMFm-1重构为高频模态分量，将剩余IMF重构为低频模态分量。

（三）分解及重构结果

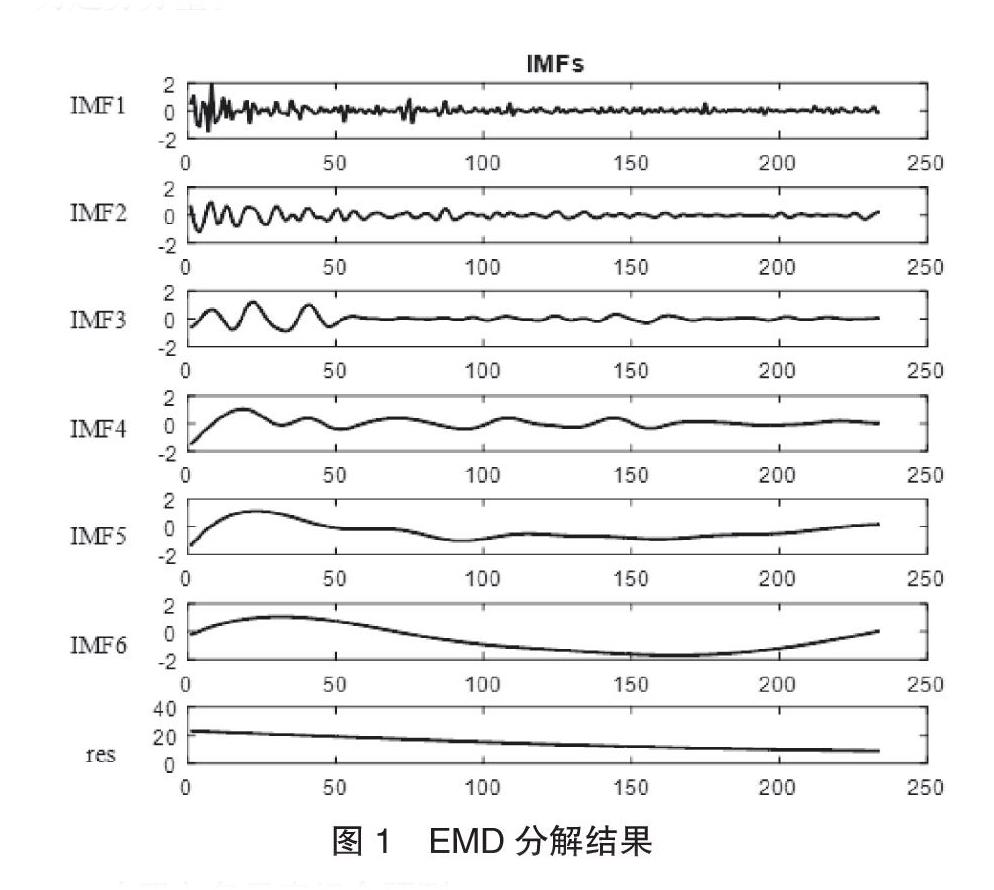
本文选取2013年4月27日份至2017年12月1日1637个日频综合利率指数（%）作为研究对象，将日频数据处理成周频数据，得到234个样本。采用EMD算法对原始数据进行分解，分解图如图1。并根据均值重构算法将IMF1-IMF4重构为高频分量，IMF5-IMF6重构为低频变量，残差项为趋势分量。

（四）多尺度组合预测

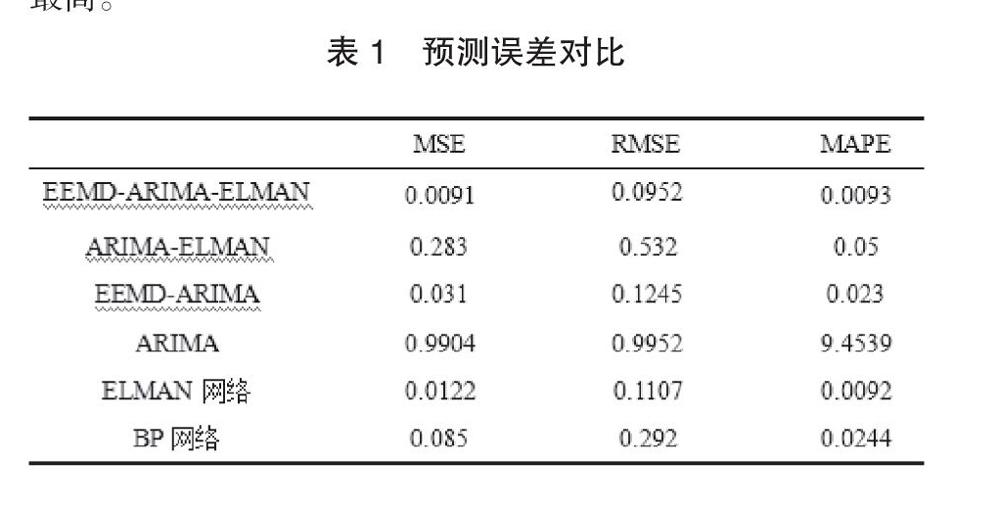
针对趋势项、低频和高频分量的波动特征，我们采用ARIMA（2，2，2）模型对趋势项进行预测，低频分量和高频分量采用ELAMN神经网络进行10期的短期预测。最后将各预测分量进行加总作为最终预测值。本文还选取了几组单一预测模型和简单组合预测进行预测误差比较，如表1显示，本文的多尺度组合预测模型的预测误差最小，预测精度最高。

四、結语

本文根据P2P网络借贷利率的非线性特征，基于分解-重构-集成的思路，探索出符合P2P网贷利率的预测方法，即多尺度组合预测法，此方法的预测效果优于一般的单一预测模型和简单组合预测模型，预测结果可为P2P网贷市场参与者的决策行为提供参考。

参考文献：

[1]陈霄，叶德珠.中国P2P 网络借贷利率波动研究[J].国际金融研究，2016a（1）：83-96.

[2]何启志，彭明生.基于互联网金融的网贷利率特征研究[J].金融研究，2016（10）：95-110.

[3]徐欢. P2P网络借贷市场的非线性动力特征研究[D].东华大学，2017.

（刘峰涛系东华大学旭日工商管理学院副教授，硕士研究生导师;侯慧敏系东华大学旭日工商管理学院硕士研究生）