混凝土防渗墙应力变形的子模型法研究
2019-08-07祁伟强覃事河贺双喜
祁伟强,覃事河 ,贺双喜 ,张 高 ,刘 曜
(1.中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081;2.国电大渡河金川水电建设有限公司,四川 阿坝 624100)
对混凝土防渗墙的数值模拟分析目前主要采用整体模型法,以往主要通过对混凝土破坏准则[1],防渗墙厚度与模型参数[2],墙底接触型式[3],接触面处理[4]等方面对防渗墙的数值模拟进行了研究,但由于防渗墙的结构尺寸相对于大坝及基础十分微小。整体模型的网格密度不能很好地与防渗墙模型匹配,通常情况下,为了计算的效率,不得不对防渗墙进行粗糙的网格划分,模拟精度也随之降低。
针对上述问题,吴秋军等[5]针对瀑布沟土石坝防渗体系采用子模型技术对防渗墙与廊道接头部位进行了计算分析,得到更加合理的数值解。张丹等[6]采用基于子模型法的三维非线性有限元对长河坝水电站大坝防渗墙与粘土心墙连接部位不同的高塑性粘土区设置方案进行了研究。
但目前对于坝基混凝土防渗墙整体应力、变形规律的研究仍然是实际工程中的一个重要问题,且对坝基混凝土防渗墙整体采用三维精细模拟研究的较少,本文主要利用子模型法的优点,采用三维子模型法对坝基混凝土防渗墙的整体应力变形规律进行研究,并结合部分实测资料进行对比。
1 子模型技术原理
子模型法又称切割边界位移法,是对部分区域的网格细化并进行分析。有限元法实质上是在求解一个线性代数方程组,而与求解对象的规模大小无关。子模型法正是基于这个思想,将需要重点分析计算的核心区域从整体模型中分离出来,然后对这些部位进行再分析,边界采用的是整体模型中位移计算结果转换而得的荷载。子模型法核心是圣维南原理:若将作用在物体小边界上的力系,转变为一个与之静力等效但是分布不同的任意力系(在子模型中即边界位移)。则小边界附近区域的的应力分布会有明显改变;而在距离小边界区域较远的范围几乎不受影响。因此,只要保证子模型的位置远离应力集中区域,子模型就能得到较精确的结果。

图1 子模型求解流程图
2 工程实例
2.1 计算模型
以某堆石坝为工程实例。最大坝高约56 m,坝基覆盖层采用混凝土防渗墙防渗,防渗墙位于坝轴线上游约84 m 处,最大深度为82 m,墙厚1.0 m。
整体模型采用8 节点六面体等参单元,单元总数为38156个,节点总数为41990 个。整体模型见图2。

图2 三维整体模型网格
对防渗墙采用子模型法模拟。子模型单元总数21000 个,节点数23715 个。模型见图3。
图3 防渗墙子模型网格
2.2 模型参数与工况
堆石料和覆盖层采用邓肯E-B 本构模拟,防渗墙混凝土采用D-P Cap 模型模拟,用节理单元[7]模拟防渗墙与顶部细料、墙体前后及墙与基础的接触关系。基岩采用线弹性模型。参数见表1、表2。

表1 坝体材料参数(邓肯E-B 模型)

表2 基岩及防渗墙材料参数
2.3 计算成果
2.3.1 施工期墙体应力变形
1)变形

表3 施工期墙体位移极值 单位:cm
由表3 计算结果可知,施工期墙体表现为5.19 cm 的沉降变形,发生在墙体顶部下游侧,沉降值大小与墙体高程成正比。墙体顺河向位移整体指向上游,最大值发生在墙体中部,最大值为16.65 cm。对坝轴向位移,上部表现为轴向压缩;下部表现为轴向拉伸。最大的轴向位移值位于墙体顶部靠近两岸侧,向右岸的最大位移为1.08 cm,向左岸的最大位移为1.12 cm。
2)应力
施工期,防渗墙第一主应力(拉为正,压为负)如图5,墙体应力极值见表4。由于墙体受坝体填筑过程的挤压作用向上游产生了较大的水平变形,使得墙体上游侧产生了一定范围的拉应力区,具体位置在墙体上游侧的顶部和靠近两岸位置,最大拉应力为1.18 MPa。防渗墙第三主应力全部为压应力,最大压应力为3.17 MPa,出现在墙体下游侧靠近底部位置。

表4 施工期墙体应力极值 单位:cm
2.3.2 正常蓄水期墙体应力变形
1)变形
由表5 和图6 可知,正常蓄水期墙体沉降仍然发生在墙顶位置,最大沉降由施工期的5.19 cm 增大到7.33 cm,这是由于防渗墙位于坝前马道下,蓄水期静水压力作用使得墙体沉降增大。蓄水期顺河向位移在渗流压力及静水压力作用下由上游转向下游,水库满蓄时,顺河向位移最大值为14.55 cm,指向下游,位置仍然在墙体中上部。蓄水后墙体轴向位移规律与施工期相似,数值上略有增大,分别为1.45 cm、1.51 cm。
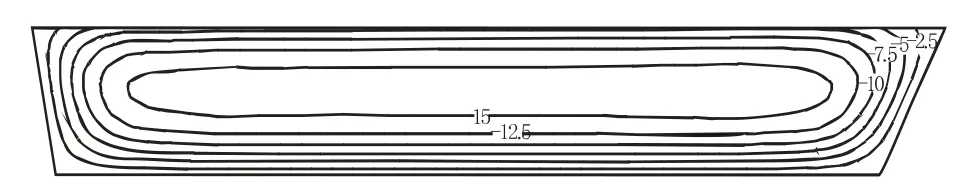
图4 墙体施工期顺河向位移(cm)

图5 墙体施工期第一主应力图(MPa)
2)应力
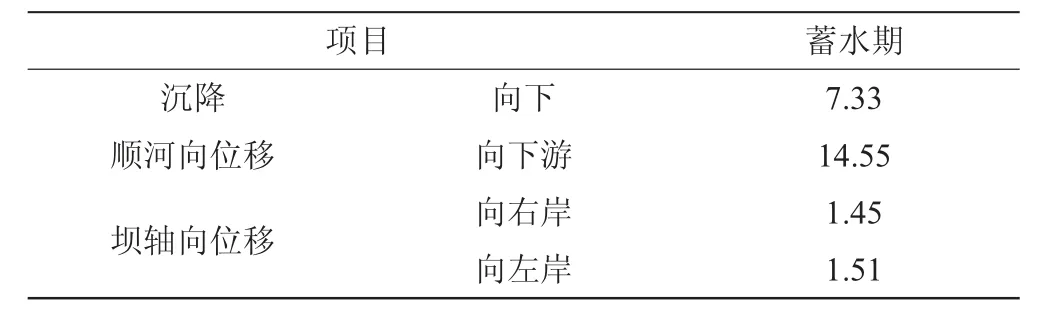
表5 蓄水期墙体位移极值 单位:cm
由图6 和图7 可知,蓄水之后,墙体在静水压力以及渗流作用下向上游的变形开始被压回,墙体的拉应力区也逐渐减少,达到正常蓄水位时,墙顶的拉应力区基本消失,墙体两岸的拉应力区较施工期也大幅减小,但是最大拉应力值较施工期有所增长,为4.1 MPa。第三主应力都为压应力,最大压应力为10.4 MPa,较施工期有较大增长,发生在墙体左岸靠近底部位置。

图6 墙体蓄水期顺河向位移(cm)

图7 墙体蓄水期第一主应力(MPa)
3 与部分监测资料的对比
3.1 顺河向位移对比
该工程坝基防渗墙布设有固定测斜仪(IN1~IN6)来监测防渗墙的顺河向位移(向上游为负)。由图8 可知,在坝体填筑的四个典型阶段,数值模拟的墙体挠度规律与监测结果的规律较为吻合,比如墙体最大位移出现位置,墙体上部和底部的位移变化趋势等。但数值上有一定差别。
3.2 沉降对比
防渗墙顶部从左岸到右岸布设有12 个沉降监测点。图9为防渗墙顶部沉降的监测值与计算值对比图。由图可以看出,数值模拟的墙顶沉降规律与监测结果类似,量值上有一定差距,原因可能有以下几个原因:1)计算模拟的大坝填筑与蓄水过程很难与实际情况完全一致;2)数值模拟中墙体由于网格划分等原因,监测节点与实际监测点位置有一定偏差。
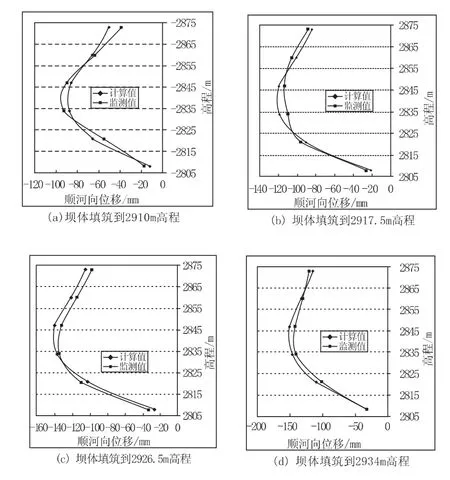
图8 防渗墙填筑期挠度曲线对比图
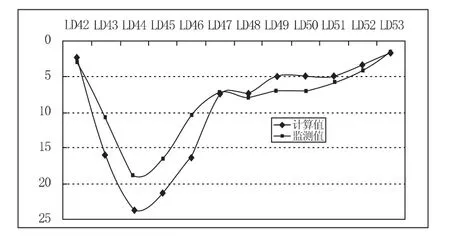
图9 防渗墙顶部沉降对比图(mm)
4 结论
1)采用子模型方法对深覆盖层上的堆石坝坝基防渗墙进行了应力变形模拟。通过与部分变形监测资料对比,证明了数值模拟结果的合理性,说明采用子模型方法对防渗墙进行模拟可行,且具有较高精度。
2)防渗墙在施工期有较大的指向上游的顺河向位移,量值为16.65 cm,位于墙体中部;墙体最大沉降发生在墙体顶部下游侧,量值为5.19 cm,且沉降值随墙体高程的增加而增大;墙体轴向位移最大值分别发生在墙体靠近两岸的顶部部位,最大值分别为向右岸1.08 cm,向左岸1.12 cm。施工期墙体上游侧顶部和靠近两岸侧有一定范围的拉应力区,最大拉应力值为1.18 MPa,墙体第三主应力全部为受压,最大压应力位于墙体下游侧靠近底部处。
3)蓄水至正常蓄水位后,墙体的顺河向位移指向下游,最大值为14.55 cm,最大沉降仍然出现在墙体顶部,最大沉降值为7.33 cm,轴向位移规律与施工期类似,量值有少许增长。蓄水后,墙体上游的拉应力区大大减少,但最大拉应力值为4.1 MPa,大于施工期的量值,建议实施时采用柔性连接,减小拉应力。第三主应力均为压应力,量值为10.4 MPa,发生在墙体靠近左岸底部处。
