一种基于GA-BP-MC神经网络的高铁桥墩沉降预测模型

冯绍权，花向红，陶武勇，宣 伟，吴 伟，续 东

(1. 武汉大学测绘学院,湖北 武汉 430079； 2. 武汉大学灾害监测和防治研究中心,湖北 武汉 430079； 3. 武汉理工大学土木工程与建筑学院，湖北 武汉 430070)

高速铁路“以桥代路”的结构特性对桥墩设计提出了更高的要求[1]，为保障高铁快速、平稳、安全运行，对桥墩进行沉降变形观测尤为重要。目前针对沉降数据预测方法主要有灰色系统理论[2]、时间序列分析[3]、人工神经网络[4-5]等。近年来，由于人工神经网络算法具有自学习和处理非线性函数等优势，广泛应用于变形预测中，其中BP(back propagation)神经网络算法应用最为普遍。然而BP神经网络自身也存在缺陷，容易陷入局部极小值和收敛速度过慢[6]。

遗传算法(genetic algorithm,GA)具有很强全局搜索能力[7]，是一种全局优化算法。马尔科夫链由于不受过去状态影响，具有无后效性[8]，对多因素影响系统预测具有一定的优越性。本文结合马尔科夫链(Markov chain,MC)和遗传算法优化BP神经网络，提出一种适合高铁桥墩沉降预GA-BP-MC神经网络预测新方法，并将本文方法应用于工程实例，通过与BP神经网络、GA-BP神经网络预测模型对比分析，验证本文方法的有效性和可行性。

1 GA-BP神经网络模型

1.1 BP神经网络原理

BP神经网络最早用于研究非线性连续函数[9]，其结构简单、易操作，是目前应用最多的人工神经网络之一[10]，它包含输入层、输出层和一层或多层隐含层，利用误差反向传播调整多层前馈神经网络的权重，改进输入层和输出层的非线性映射关系[11]。BP神经网络具有自学习、自适应、分布式存储等特点，目前已被广泛应用于非线性预测[12-13]。

1.2 遗传算法优化BP神经网络结构

遗传算法是一种基于自然选择和遗传理论的随机优化算法，通过选择、交叉和变异等操作对所有个体进行筛选，根据适应度值保留优秀个体，淘汰适应度差的个体[14]。遗传算法优化过程[15-17]主要包括编码、确定适应度函数、选择操作、交叉操作、变异操作5个方面，具有很强的全局寻优能力。

BP神经网络是按照梯度下降的方法求取误差函数最小值的过程，对初始权值等网络参数十分敏感，全局搜索能力较差，易陷入局部最优，本质是一种局部优化方法；遗传算法优化网络结构时不依赖于梯度，采用选择、交叉和变异操作进行搜索，具有很强的全局搜索能力。用遗传算法优化BP神经网络结构可以结合二者的优势，弥补BP神经网络的缺陷，其基本原理是发挥遗传算法的全局搜索能力，优化网络的初始权值和阈值，使其搜索范围缩小至全局最优附近，随后利用神经网络非线性逼近能力，达到快速收敛的效果。

2 GA-BP-MC神经网络模型

2.1 MC预测值修正模型

马尔科夫链是一种无后效性随机过程，可根据系统当前时刻状态推求下一时刻的状态概率分布，从而确定下一时刻状态[18]。时间序列统计量多数都具备马尔科夫链特性，利用这种特性可以进一步提高模型的预测精度。利用马尔科夫链修正GA-BP神经网络模型具体步骤如下：

(1) 状态划分：根据GA-BP神经网络模型预测值的相对误差大小和分布密度，采用最值均方差法将相对误差区间分成n个状态[18]，即S=(S1,S2,…,Sn)。其中n的计算方法为

n=EVEN(d/σ)

(1)

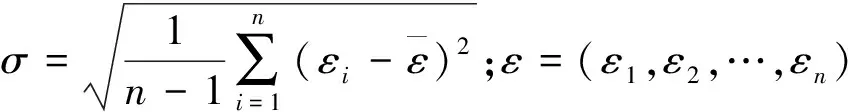
(2) 状态转移概率矩阵[19]：相对误差Si经k时步状态转移到状态Sj的概率为

(2)

式中，Mij(k)是Si经k时步状态转移到状态Sj的次数；Mi是相对误差在状态Si出现的次数。

进行系统预测一般只需考虑1时步状态转移矩阵，即

(3)

莲心碱对佛波酯所致耳肿胀炎症模型小鼠的抗炎作用及机制研究 ………………………………………… 姚 茹等（17）：2364

(3) 预测值修正：本文取预测的相对误差状态所处区间中点为预测值的相对误差[20]，预测值修正值为

(4)

式中，ΔD、ΔU分别为预测的相对误差所处状态区间的上下限值；f(x)为GA-BP神经网络的预测值。

2.2 GA-BP-MC神经网络模型构建

本文结合马尔科夫链理论和遗传算法优化BP神经网络模型主要过程为：首先初始化神经网络结构；然后用遗传算法优化的网络初始权值和阈值训练并保存神经网络；最后结合MC模型修正GA-BP神经网络模型预测值，具体过程如图1所示。

3 高铁沉降预测实例

3.1 试验数据

高速铁路建设和运营过程中，为保障列车安全、平稳高速运行，对高铁桥墩进行定期监测具有十分重要的意义。本文对某城际铁路某桥墩20期定期沉降监测数据[1]进行预测，实测累计沉降值见表1。

表1 监测点实测累计沉降值

3.2 试验与结果

本文结合GA-BP-MC神经网络预测模型，利用前17期数据滚动式[21]预测后3期数据。以第1—5期实测累计沉降数据为网络输入，第6期数据为网络输出；类推至以第12—16期数据为网络输入，第17期数据作为网络输出，组成网络训练样本。用训练好的GA-BP神经网络预测后3期的数据，将所得的预测值用MC模型进行修正，得到GA-BP-MC网络预测值，分析优化后GA-BP-MC神经网络预测模型精度。预测精度评定指标有绝对误差(absolute error)、误差绝对值均值(mean absolute error,MAE)、平均绝对百分误差(mean absolute percentage error,MAPE)、误差均方差(mean squared error,MSE)。

为加快网络训练速度，将实测累计沉降数据进行归一化处理。利用基于L-M优化算法的BP神经网络反复训练和对比，当隐含层神经元数目为8时，网络拟合效果最好。

为了验证本文算法的可行性和有效性，选择与BP神经网络模型和GA-BP神经网络模型结果进行对比。3种网络模型的网络训练次数均为1000次，目标误差均为0.000 1，学习速率均为0.05，并设定遗传算法种群规模为50，遗传代数为100，变异概率为0.05，交叉概率为0.6，选择概率为0.08。

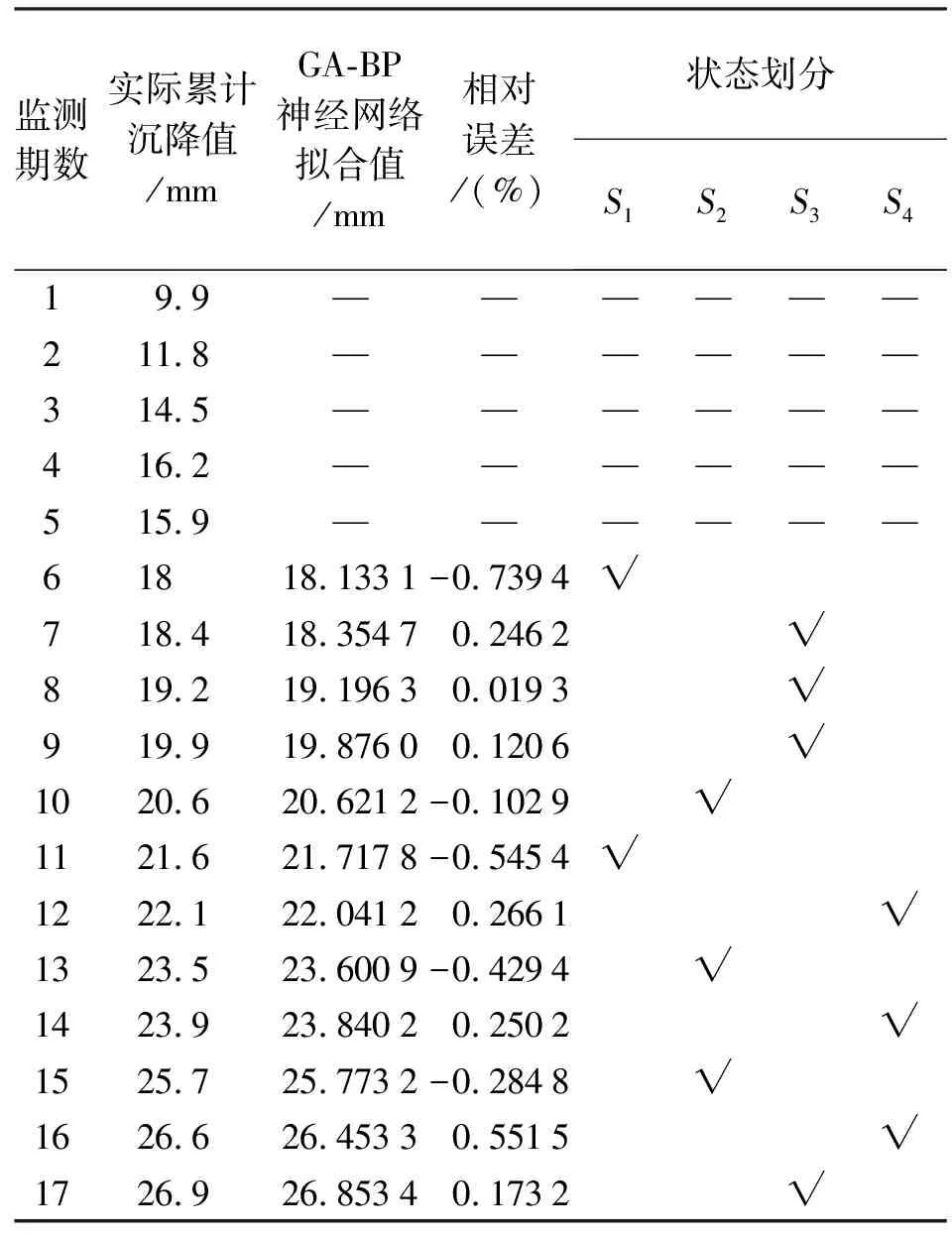
监测期数实际累计沉降值/mmGA-BP神经网络拟合值/mm相对误差/(%)状态划分S1S2S3S419.9——————211.8——————314.5——————416.2——————515.9——————61818.1331-0.7394√718.418.35470.2462√819.219.19630.0193√919.919.87600.1206√1020.620.6212-0.1029√1121.621.7178-0.5454√1222.122.04120.2661√1323.523.6009-0.4294√1423.923.84020.2502√1525.725.7732-0.2848√1626.626.45330.5515√1726.926.85340.1732√

表3 累计沉降预测值比较

图3为各模型累计沉降预测值。由图3定性分析可知，GA-BP-MC神经网络模型3期预测值与实际累计沉降值接近，预测效果比其他两种好。从表3定量分析可知，GA-BP神经网络预测模型的绝对误差较传统BP神经网络预测模型最大优化值为0.334 9 mm，可见遗传算法可以提高BP神经网络预测模型精度；本文基于MC理论继续优化GA-BP神经网络模型，最小绝对误差达到0.007 6 mm，在GA-BP神经网络模型的基础上预测精度得到进一步提升。

为进一步分析本文所建模型预测精度，分别计算各预测模型的MAE、MAPE、MSE，见表4。由表4可知，GA-BP-MC神经网络预测模型较GA-BP神经网络预测模型在MAE、MAPE、MSE 3项精度指标上分别提高了40.11%、39.65%、37.98%，较传统BP神经网络预测模型分别提高了81.19%、81.08%、79.31%。综合分析3种神经网络预测模型，可见遗传算法全局寻优能力提高了传统BP神经网络预测模型精度，结合MC理论根据训练数据相对误差的转移概率矩阵确定预测值相对误差状态，可进一步提高了预测值精度，验证了本文算法的有效性。

4 结 语

为了建立适合高铁桥墩沉降预测模型，本文结合马尔科夫链和遗传算法理论优化BP神经网络，建立了GA-BP-MC神经网络预测模型，通过实际工程数据分别与BP神经网络预测模型和GA-BP神经网络预测模型进行对比分析，结果表明了本文预测模型精度更高，验证了GA-BP-MC神经网络沉降预测模型的有效性和可行性。

表4 各预测模型预测精度比较