基于改进非线性趋近律的桥式起重机滑模控制

2019-08-07强宝民何祯鑫杜文正

兵器装备工程学报 2019年7期

王杰，强宝民，何祯鑫，杜文正

(火箭军工程大学导弹工程学院，西安 710025)

桥式起重机作为一种典型的欠驱动设备，在工业生产中有广泛的应用。所谓欠驱动系统，是指系统的独立控制变量个数小于系统自由度个数的一类非线性系统，在生产实践中很多设备都具有欠驱动的形式，由于去掉系统部分驱动器，增加了系统自由度，提高了系统灵活性，并且在节约能源、降低价格、减轻质量、增强系统适应性等方面都欠驱动系统都比全驱动系统优越，但系统中存在非直接控制的摆动自由度，给系统的稳定控制带来了难度。因此对桥式起重机的防摆研究，不论对于控制理论的完善，还是实际工业生产都有极其重要的意义。

近年来，国内外学者针对桥式起重机系统的控制问题开展了很多研究工作，主要控制方法可以分为线性控制与非线性控制。H.Saeidi等采用神经网络自整定方法调节PD参数[1]；M.Solihin通过遗传优化方法设计稳定的鲁棒PID控制器[2]；M.Adeli等设计了一种与遗传算法相结合的并行分布式模糊LQR控制器[3]。Khatamianfar等利用模型预测控制方法对桥式起重机的防摆控制进行了广泛的研究，提出了基于模型预测控制的约束欠驱动状态(如摆角)的方案[4]；Chiu 等使用梯度下降法对递归神经网络(RNN)进行参数在线调整[5]；方勇纯团队将能量法应用到桥式起重机的消摆控制中，并加入自适应控制，增强了系统的适应能力，取得了丰硕的研究成果[6-7]。

对于桥式起重机系统而言，现阶段主要控制目标为快速且准确的台车定位与负载摆动的抑制消除，由于系统自身的欠驱动特性，加之多数负载具有双摆效应[8]，甚至发生吊绳方向的轴向扭转[9]，因此系统具有极强的不稳定性，同时，在生产中极易出现短时强风[10]等外界干扰，如不加有效控制，收敛速度很慢，严重影响生产效率。

滑模控制具有对参数摄动和外界干扰不敏感的特点，被越来越多的研究人员用来处理桥式起重机系统的控制问题。根据文献[11]提出的桥式起重机分级滑模控制方法，针对本文的研究问题，将系统分成两个二阶子系统，先就各子系统设计第一层滑动面，再定义第二层滑动面，依据第二层滑动面的稳定条件得出控制输入。通过使用分层滑模控制，实现了系统多目标控制到单目标控制的转换，简化了系统的控制设计。之后针对等速趋近律引起的系统高频抖振问题，提出了改进的非线性趋近律，实现了快速趋近，削减抖振。

1 桥式起重机系统数学模型

对于常见的二维定绳长桥式起重机示意图如图1，M，m分别为台车和负载的质量，l为吊绳质量,u(t)为控制输入，θ为负载偏角，fr为轨道摩擦力，采用欧拉-拉格朗日方法建模为[12]：

(1)

(2)

方程式(1)、式(2)可改写为欠驱动系统的一般形式：

(3)

其中，x=[x1,x2,x3,x4]T为系统状态向量，分别代表台车速度、加速度、负载偏角以及角速度，u(t)为控制输入，f1,f2,g1,g2为状态向量的非线性函数，表示为：

(4)

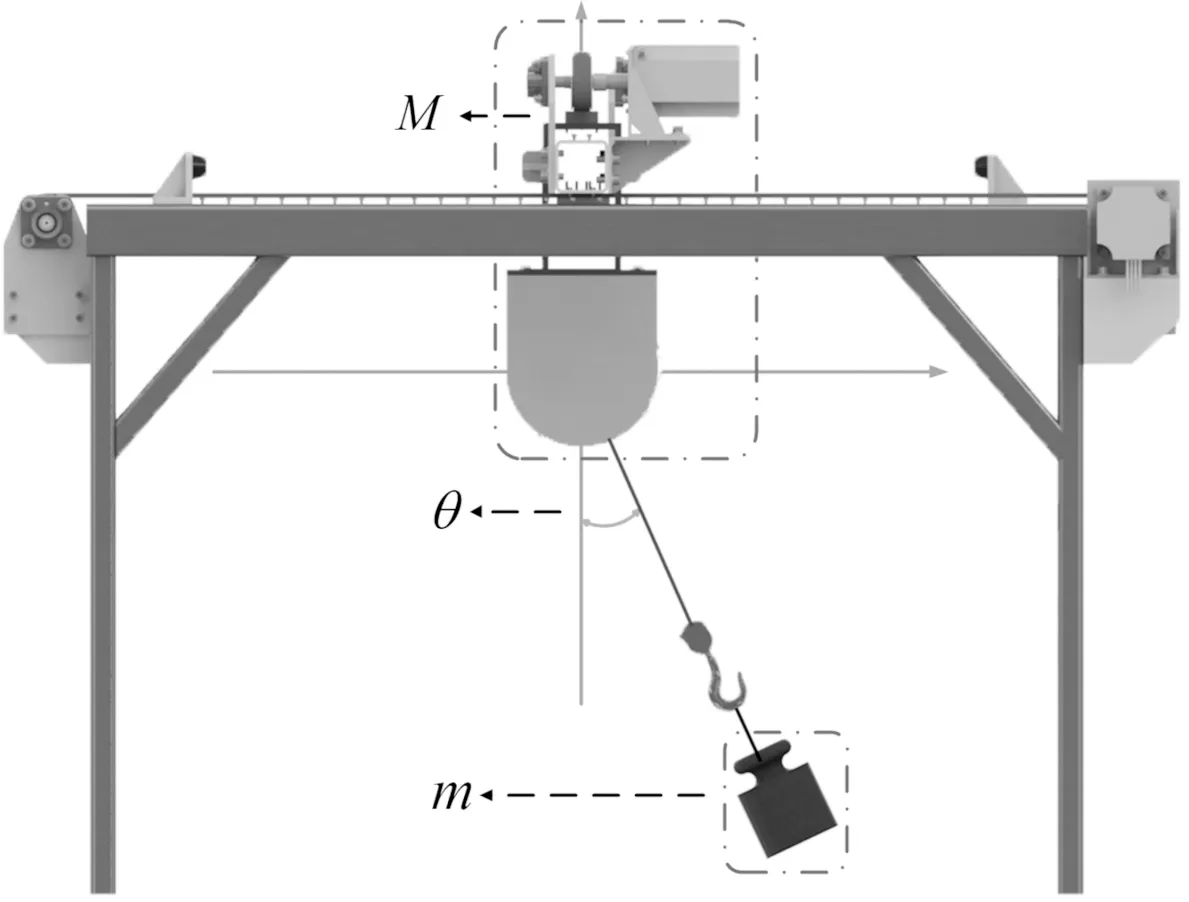
图1 二维桥式起重机示意图

2 基于控制律的分层滑模控制器设计

考虑式(3)所示欠驱动系统的一般形式，X=[x1,x2,x3,x4]T为系统状态变量，x1,x2是台车的速度、加速度信息，x3,x4是负载的摆角以及角速度信息，因此可采用两层滑模面保证系统的稳定性。将整个欠驱动系统的状态定义为[x1,x2]T位移子系统和[x3,x4]T摆角子系统，针对每个子系统所设计的子滑模面满足李雅普诺夫稳定性理论因此子滑模面是渐进稳定的，之后定义的总滑模面是子滑模面的线性组合，因此能够保证子滑模面快速收敛[13-14]，进而实现整个欠驱动桥式起重机系统的稳定与快速收敛。首先定义子系统滑模面：

(5)

其中c1,c2为严格正实数。

由等效控制原理求得等效控制量：

(6)

为了保证包含两个子系统的总系统稳定，需要设计第二层滑模面：

S=α2s2-α1s1

(7)

其中，α1,α2为严格正实数。

为保证子系统能够到达第一层滑模面，设计系统总输入为：

u=ueq1+ueq2+usw

(8)

为了获得整个系统的控制输入量，需要确定切换控制部分。对基于分层滑模控制方法的变结构控制器而言，系统第二级滑动面的稳定性保证了变结构控制系统的整体稳定性，因此切换控制量usw的选取应使滑模到达条件成立：

(9)

采用等速趋近律求解滑模控制器的切换控制量[15]，即

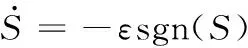
(10)

其中，ε为严格正实数。

由式(7)、式(10)求得滑模控制器切换控制量：

(11)

进而求得基于等速趋近律的分层滑模控制器总输入：

u=ueq1+ueq2+usw=

(12)

由式(12)可知，整个起重机系统的控制输入量中含有符号函数这一不连续项，该不连续项的存在将导致变结构系统出现抖振现象，且系统的抖振程度取决于系统参数的大小。为获得较短的稳定时间和鲁棒性，需要选择较大的控制器增益，这会导致系统的大幅高频抖振，为解决系统抖振与控制效益的矛盾，本文在文献[16]中的基础上提出了式(13)表示的非线性趋近律：

(13)

其中：k,ε为正实数；p为介于[0,1]区间的正实数；γ为正实数；χ为正整数。由式(13)求得：

(14)

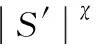
式(14)表明，滑模到达条件式(9)成立，因此系统的第二层滑动面S′是稳定的，从而确保整个控制系统处于稳定可控状态。此时系统控制输入为：

(15)

3 控制系统快速性分析

根据式(10)和式(13)所示等速趋近规律和非线性趋近规律，有趋近速度：

(16)

由式(16)得，对非线性控制规律而言，当系统状态远离平衡点时，即S′≫1，由式(13)得此时非线性趋近律中，ε/Q(S′)无限趋近于ε/p，而ε/p>ε，从而趋近过程中，ε/Q(S′)>ε使得系统状态的稳定趋近速度加快，与此同时，当系统状态接近稳定时，即S′→0，此时的系统趋近速度接近于ε，因此在系统的趋近过程中，趋近速度由ε/Q(S)逐步下降到ε，使得非线性趋近律项满足ε<ε/Q(S)<ε/p，进而抑制了系统抖振，同时也使得控制器能够动态地适应S′的变化。对等速趋近律而言，趋近速度稳定在ε，趋近速度无法进行动态调整，从而会引起大幅高频抖振。

收敛性定理:针对相同的控制系统，非线性趋近律具有更短的到达时间。

证明：由非线性趋近律式(13)，并设到达时间为t1，可得：

(17)

由于Q(S)>0，且S(t1)为零，将式(17)化简并在[0,t1]进行积分，可得：

(18)

对等速趋近律而言，S(t2)为零，同理可得：

t2ε=|S(0)|

(19)

由式(18)、式(19)得：

(20)

因此非线性趋近律相比等速趋近律，具有更短的趋近时间，因此能够达到更好的控制效果。

4 稳定性分析

稳定性定理一:对于二维定绳长桥式起重机系统，若采用式(5)所示设计子系统滑模面，式(7)所示总滑模面，并采用式(15)所示总滑模控制量，则整个桥式起重机系统的滑模面是渐进稳定的。

证明：构造Lyapunov能量函数

(21)

(22)

由之前对系统的快速性分析可知：

ε<ε/Q(S)<ε/p

(23)

因此，由式(22)可进一步得

(24)

对式(24)进行积分运算，进一步有

(25)

进而

(26)

V(0)<∝

(27)

稳定性定理二:对于二维定绳长桥式起重机系统，若采用式(5)所示设计子系统滑模面，式(7)所示总滑模面，并采用式(15)所示总滑模控制量，则各子滑模面也渐进稳定。

证明：由式(27)得到：

(28)

即总滑模面为绝对可积，构造两个滑模面：

(29)

(30)

进而有：

(31)

由式(27)、式(30)可知

(32)

从而得出：

(33)

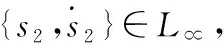
5 仿真分析

为了进一步分析本文桥式起重机控制方法的有效性与可行性，采用Matlab/Simulink进行数值仿真试验验证。分别针对等速趋近律、改进趋近率进行系统的稳定性分析论证；针对两种趋近律分别分析滑模面的收敛情况；分别针对控制输入分析系统抖振情况，最后对系统对干扰的鲁棒性进行试验分析，检验控制方法的稳定性、收敛速度以及抖振抑制性能在实际工况中的应用效果。

仿真试验期望位置设置为2 m，桥式起重机系统参数分别设置为：台车质量m=9.5 kg，负载质量M=10 kg，绳长l=1 m，参数c1=0.55，c2=4.9，α1=2.15，α2=2.85，ε=3，k=0.55，p=0.1，χ=1。

采用普通等速趋近律的系统控制响应曲线如图2所示，采用改进的非线性趋近律的系统控制响应曲线如图3所示，两种趋近律的子滑模面与总滑模面函数曲线如图4所示。

图2 基于等速趋近律控制响应曲线

图3 基于非线性趋近律控制响应曲线

图4 分层滑模控制滑模面函数曲线

通过仿真，由图1、图2可以看出，改进非线性趋近律的控制品质较等速趋近律基本相同，等速趋近律能够在6 s内完成系统收敛，非线性趋近律能够在4 s左右完成系统收敛，但相比之下，改进趋近率能够较等速趋近律大幅减小系统切换抖振。由图3看出，两种控制方法的滑模面都能够在有限时间内趋近于零，因而验证了控制方法的稳定性。

对于桥式起重机复杂的工况条件，本研究采用高斯噪声对系统鲁棒性进行验证，在8 s处定义干扰为：

(33)

仿真试验取噪声信号幅值A=2，参数ci=8，bi=0.3，得到系统控制输入和状态响应曲线如图5所示，滑模面函数曲线如图6所示。