辐射流立方定理的推导及试验研究

丁林楠， 柴军瑞， 覃 源， 许增光

(西安理工大学 西北旱区生态水利工程国家重点实验室， 陕西 西安 710048)

1 研究背景

对于裂隙流的研究，是从长直流光滑平行板的提出开始。著名的立方定理，正是对光滑平行板中水流特性的定性描述。然而，立方定理的适用性存在许多限制条件。例如，隙宽和水力梯度是恒定值，流速梯度与流动方向相垂直[1]。天然裂隙并不完全满足以上条件，导致实际流速偏离了立方定理的预测值[2-3]。卢占国等[4]对实际平行裂隙下的立方定理进行修正，并根据隙宽和流速划分了线型渗流和非线性渗流。朱红光等[5]根据粗糙度对水流产生的非线性影响，建立了岩石裂隙非线性几何模型。

许多学者在研究隙宽空间变化的基础上，得到了局部立方定理[6]。局部立方定理的应用同样存在假设前提，例如结构面的中和面为平面并且每一个局部点都满足立方定理[7]。然而，由于曲折度的存在使以上条件很难满足。学者们从不同方面探讨了局部立方定理的适用性。对于不对称结构面，有学者通过限制结构面的几何特征验证局部立方定理的有效性[8-9]。局部立方定理由Stokes方程推导而出，其忽视了惯性力的影响。因此，Alyaarubi等[10]认为低惯性力是局部立方定理的适用条件，并根据理论分析和试验将限制条件定为Re<1。Wang Lichun等[7]在考虑曲折度、粗糙度和Re数的影响下，对局部立方定理进行了修正。Mgaya等[11-12]基于深度平均的Navier-Stokes方程建立了新的模型，通过该模型得到的数值结果与试验值具有较高的吻合度[13]。Kishida等[14]发明了一种同时包含渗流试验和隙宽测量的试验系统，通过该系统研究了不对称单裂隙结构面的渗流规律。

不论是立方定理还是局部立方定理，以上的研究均集中在长直流方面。研究表明，钢筋混凝土衬砌在高水头作用下，容易产生裂缝，导致围岩直接承受高压水的作用[15]。其渗流方式不同于长直流，而是由内向外的辐射流。这时的平行板二维模型将不再适用，取而代之的是三维辐射流。Cao Cheng等[16]在试验基础上提出了辐射流立方定理的半理论半经验公式。本文进一步研究辐射流，通过理论分析推导辐射流立方定理。根据水力试验，研究立方定理对平行板和规则齿幅射流的适用性。

2 辐射流平行板

本文所讨论的辐射流光滑平行板，由两块光滑、平直的圆形平行板组成，注水孔位于平行板的圆心。水流由中心注水孔向四周均匀扩散。为了与下文的水力试验相匹配，将中心注水孔设置在下试件。几何形状示意图如图1所示。

图1 辐射流光滑平行板几何示意图

2.1 辐射流平行板水流分布特性

对于岩体裂隙而言，流体的运动受N-S方程控制(3组非线性偏微分方程)，可以按公式(1)表达[1]：

(1)

式中:u为速度矢量，m/s；μ为流体的动力黏滞系数，kg/(m·s)；P为水压力，Pa；f为单位质量力，N；ρ为流体的密度，kg/m3。N-S方程描述了流场中流体所受到的惯性力、压力、黏性力和质量力之间的演变关系。N-S方程本身不闭合，在求解变量(u,P)时，需要配合流体的质量守恒方程共同进行求解，对于不可压缩流体，质量方程为[7]：

▽·u=0

(2)

运用Prandtl边界层分析法[17]，分析惯性力和黏性力具有相同数量级的黏性区范围，沿流动方向对水流进行受力分析，如图2所示。

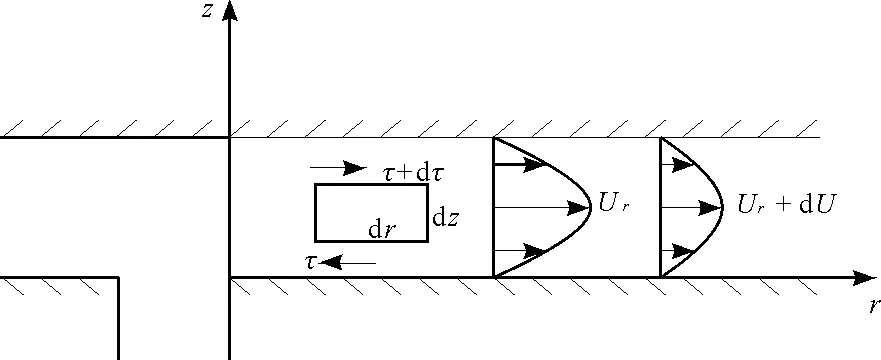
图2 流动方向上流体的惯性力和黏性力示意图

惯性力大小：

(3)

黏性力大小：

(4)

数量级关系：

(5)

本文用δ表示z方向上的特征长度；用辐射范围半径R与中心注水孔半径r0的差值△r=R-r0表示r方向的特征长度，并称之为净辐射范围；水流沿径向的平均速度U为r方向的特征速度。将以上特征值代入公式(5)，可得：

(6)

对于饱和裂隙流而言，辐射流湿周χ=2πr×2，过水断面面积A=2πr·b，水力半径R=A∕χ=b/ 2。Re数的特征长度为水力半径的4倍，故辐射流的特征长度为隙宽的2倍[18]。

(7)

式中：ν为流体的运动黏滞系数，m2/s；b为裂隙隙宽，m。

根据流量守恒原理，辐射流平行板的水流在向外辐射的过程中，流速由内向外逐渐减小。由公式(6)知，惯性力的削弱与流速的二次方成正比，而黏性力的削弱与流速的一次方成正比。随着水流向外流动，惯性力的作用将逐渐被黏性力取代。当入射水流具有较大Re，即惯性力较大时，水流呈现出两种状态，惯性力起主导作用的势流区和惯性力、黏性力旗鼓相当的黏性区，本文将这一段距离称为“强惯性带”。辐射过程中水流的流速变化如图3所示。

图3 辐射过程中流速分布变化示意图

随着惯性力的削弱，当惯性力相对黏性力可以忽略时，称水流处于“弱惯性带”。

(8)

公式(8)与公式(6)在黏性力的表述方面有所不同，公式(8)中黏性区厚度δ由隙宽b取代，此时的裂隙流完全处于黏性区。 本文用ε表示中心注水孔半径r0与辐射范围R的比值，并称之为辐射比。为了同时考虑净辐射范围和辐射比的影响，用中心注水孔处的初始Re0判断水流能否进入弱惯性带。

(9)

2.2 辐射流立方定理

在辐射流平行板中，当内外水头差恒定时，水流在平行板中形成恒定流。对于不可压缩的恒定渗流，当其渗透系数不存在各向异性时，水头函数满足Laplace方程，其柱坐标下的形式[19]为：

(10)

根据Darcy定理，辐射流平行板上的流量与水头梯度成正比,即：

(11)

式中：k为裂隙的水力传导系数。

由公式(10)、(11)得到流量随总水头的变化关系：

(12)

通过N-S方程求解水力传导系数k。其在柱坐标下的形式[20]为：

(13)

根据2.1节关于辐射流平行板水流分布特性的研究，当水流的初始Re0满足公式(9)时，惯性力可以近似忽略。假设满足此条件，对N-S方程简化：

(14)

通过数量级分析法对比分析公式(14)中的黏性力项。隙宽b的量级比辐射范围r的量级小，而z与b的量级相同。令φ≪1，表示b的量级；用1表示r和Ur的量级。公式(14)中黏性力的两项，量级分别为-Ur/r2∽1/1, ∂2Ur/∂z2∽1/φ2。为了使∂2Ur/∂z2的量级为1，运动黏滞系数ν的量级必为φ2。略去高阶无穷小量后，对流速Ur沿隙宽积分，单宽流量q与水力传导系数k分别为：

(15)

(16)

将k值代入公式(12)得辐射流立方定理：

(17)

3 水力试验

3.1 试验系统

本次试验采用TJXW-600型微机控制岩石节理直剪渗流耦合试验机。该试验机由电液伺服加载系统、多通道闭环测控系统、渗流调控系统等组成，其基本结构示意图和实物图如图4所示。

试验系统可提供法向与切向荷载来模拟实际岩体裂隙的受力情况。法向荷载与切向荷载由静音式伺服油源提供，其最大荷载值均为600 kN。试验系统在法向方向上的可控边界条件为常法向应力(CNL)，可用来模拟法向应力不变的无支护边坡稳定问题。

力传感器采用轮辐式负荷压力传感器，不同应力下应变片的阻值有所不同，通过测量不同阻值下电压的变化，并通过后续的仪表放大器进行放大来精确测量荷载值，所得荷载示值精确度为±1%。位移传感器采用拉线式，将机械位移量转换成可计量的电信号来精确测量位移，切向位移精度为0.04 mm，法向位移精度为0.003 mm。渗流增压系统采用气压加压方式，将氮气、水箱及剪切盒有效连接。其最大水压力达3 MPa，储水量为10 L。在出水口的集水计量装置处设置流量测量装置，可精确测量不同水压下的流量，流量示值精确度为±0.1%。Multli-05全数字多通道闭环测控仪采用先进的自适应PID算法，使系统参数的控制量得到线精度的闭环控制，从而实现等速加载卸载、恒定法向力、恒定法向位移等功能。密封剪切盒由上、下两部分组成，下试件固定并钻有中心注水孔，上试件与加载器直接接触，可发生移动。渗水从下试件中心注水孔注入，向四周流动。

3.2 试件及试验方案

立方定理建立在理想的光滑平行板结构，而天然裂隙的轮廓线并非平直、光滑。为了验证立方定理的适用性，制作了光滑平行板和规则齿两种试件。试件用石膏材料和水按质量比为4∶1搅拌均匀后，注入特定模具中，等试件凝固硬化后脱模。中心注水孔半径为4 mm，辐射范围R=100 mm。试件如图5所示。

由于TJXW-600试验机不具有测量初始隙宽的功能，在试件之间放置0.3 mm厚度的金属垫片充当初始隙宽，利用线性变位计(LVDT)获取隙宽值的变化。

图4 TJXW-600型微机控制岩石节理直剪渗流耦合试验机

图5 试验试件实物图

光滑平行板用来验证光滑、平行状态下立方定理与实际过流能力的吻合程度；规则齿用来研究立方定理对于粗糙裂隙面的适用性。对光滑平行板和规则齿分别在0.1、0.2和0.4 MPa水压下进行水力试验，试验方案如表1所示。

表1 水力试验方案

3.3 试验结果及分析

不同方案流量随隙宽的演变如图6所示。水力压强为0.1 MPa时，平行板和规则齿的流量基本相同。随着水力压强的增大，规则齿的流量将小于平行板的流量。在初始隙宽0.3 mm处，相比于平行板，规则齿的流量在水力压强为0.2、0.4 MPa时分别减小7.9%、14.6%。6种试验方案在单位水头下流量Q/ΔH随隙宽的演变，如图7所示。在0.1 MPa水力压强下，平行板的流量与立方定理吻合良好，规则齿的流量略小于平行板。随着水力压强的增大，实际流量将小于预测流量。水力压强为0.2、0.4 MPa时，平行板的流量平均比立方定理分别小28.9%、32.9%。

以上结果表明，粗糙度和水力压强的增大，都会使水流偏离线性Darcy流，表现出非线性流特性。用Forchheimer公式[19]表述(公式(18))，非线性流的出现使相同水力梯度(J)下的流速(v)减小，从而导致流量相对预测值下降。

J=av+bvm

(18)

式中：a、b为常数，与水力传导系数相关；m与流态相关，m=1属于层流渗流，m=1～2为过渡区渗流，m= 2属于粗糙区渗流。

图6 各试验方案下流量随隙宽的演变

图7 单位水头下流量随隙宽的演变

根据上文对立方定理的推导，其初始Re0需满足公式(9)。在水力试验中，隙宽从0.3 mm逐渐减小，初始隙宽0.3 mm对应Re0的边界限制条件。将立方定理和初始隙宽代入公式(9)，得到水头的限制条件 4.732 m。而在水力试验结果中，水力压强为0.1 MPa(约10 m水头)时，平行板流量依然满足立方定理，表明通过公式(9)判断平行板是否满足立方定理偏于安全。

4 结 论

本文通过理论分析推导了辐射流光滑平行板下的立方定理，并进行水力试验研究和总结其适用性。

(1)根据对辐射流立方定理的理论推导，将其适用性总结为：裂隙结构面满足光滑平行板结构；裂隙流属于线性Darcy流；水流在辐射过程中，可以进入忽略惯性力的弱惯性带。

(2)立方定理可以准确预测光滑平行板的流量。但是，高水头差会造成非线性水流的产生，导致流量偏离立方定理。通过公式(9)初始Re0的限制条件，可以判断水流是否满足线性流，从而满足立方定理。由水力试验结果知，该公式偏于安全。

(3)粗糙度的存在会破坏水流的连续性，从而削弱裂隙面的过流能力。

对于存在粗糙度的裂隙面，可以用立方定理近似估计流量。当精确度要求较高时，则需要对不同粗糙度下的立方定理进行修正。本文并未进一步展开研究，将在后续研究中进行讨论。