有效Hamilton函数存在唯一性的一个几何证明
2010-09-13乔元波朴大雄
乔元波,朴大雄
(中国海洋大学数学科学学院,山东青岛266100)
有效Hamilton函数存在唯一性的一个几何证明
乔元波,朴大雄
(中国海洋大学数学科学学院,山东青岛266100)
本文参考Fathi和Siconolfi的思想,对拟凸的Hamilton-Jacobi方程的有效Hamilton函数的存在唯一性给出一个几何化证明,并给出有效Hamilton函数H(P)的5个不同表达式。
拟凸Hamilton函数;有效Hamilton函数;Hamilton-Jacobi方程;黏性解
0 引言
考虑Hamilton-Jacobi方程H(x,P+Du)=a,a∈R为参数。Lions,Papanicolaou和Varadhan曾证明了如下结果[1]:
当H∈C(TN×RN)且|lpi|m→∞H(x,p)=+∞对x∈TN一致成立时,存在唯一的a∈R使得方程H(x,P+ Du)=a存在全局黏性解,记此唯一的a∈R为H(P),称为有效Hamilton函数,其中TN表示平坦环面, p∈RN为变量,P∈RN为常量。
他们通过考虑逼近方程H(y,P+Dyvα)+αvα=0的解来证明了H(P)的存在性,通过采用比较原理和反证法证明了H(P)的唯一性。
Fathi和Siconolfi[2]考虑了拟凸的Hamilton-Jacobi方程H(x,Du)=a,并对此方程证明了上述结果。他们的证明是一种几何化的证明方法,简单自足,并且给出了H(0)的一个表达式:
H(0)=inf{a:方程H(x,Du)=a存在黏性下解}。
另外,Fathi[3]使用Lax-Oleinik半群也证明了类似的结果。另见Evans[4]。
本文根据一个基本的事实,即凸集平移之后仍为凸集,参考Fathi和Siconolfi思想,对拟凸的Hamilton-Jacobi方程的有效Hamilton函数的存在唯一性给出一个几何化证明,并给出H(P)的5个不同表达式。
1 基本假设与预备知识
关于Hamilton函数H的一些假设。TN表示平坦环面,其上赋予由RN上的欧氏度量诱导的平坦的黎曼度量。Hamilton函数H定义在TN的余切丛T TN= TN×RN上,且满足:H(x,p)=+∞对x∈TN一致成立。
B(x,r)表示中心为x,半径为r的开球。对于RN中的任一集合C,d(·,C)表示到集合C的距离,通过公式d#(·,C)=2d(·,C)-d(·,∂C)定义到集合C的有向距离。当集合C为凸集时,有向距离d#(·,C)为一凸函数。若C为一凸闭集,则对任意v∈RN,定义σC(v)=sup{pv:p∈C},定义点p∈C关于C的法锥为NC(p)={v:pv=σC(v)}。
下面给出黏性解的定义。
定义1 (黏性解)称连续函数u:TN→R为方程H(x, P+Du)=a的一个黏性下解,若对任一C1函数φ:TN→R,φ≥u,在每一使得φ(x0)=u(x0)的点x0满足H(x,P+Dφ)≤a;称连续函数u:TN→R为方程H(x,P+Du)=a的一个黏性上解,若对任一C1函数φ:TN→R,φ≤u,在每一使得φ(x0)=u(x0)的点x0满足H(x,P+Dφ)≥a;若函数u既为黏性下解,又为黏性上解,则称u:TN→R为方程H(x,P+Du)=a的一个黏性解。
称上述定义中的检验函数φ为一条上切线,φ为一条下切线。
定义2 (严格黏性下解)称一个黏性下解u:TN→R为方程H(x,P+Du)=a在点x0的一个严格黏性下解,若存在点x0的一个开邻域Vx0和某一ax0 对任意x∈TN,a∈R, (H2){(y,p):H(y,p)≤a}为紧集; (H3){p:H(x,p)≤a}为凸集; (H4)∂{p:H(x,p)≤a}={p:H(x,p)=a},其中∂A表示集合A的边界。 注1 条件(H2)等价于Hamilton函数H强制,即u|Vx0为方程H(x,P+Du)=ax0的一个黏性下解。称一个黏性下解u:TN→R为方程H(x,P+Du)=a在开集B上的一个严格黏性下解,若对几乎所有的x∈B,H(x,P+Du)≤a 对某一a 对任意给定的a,x,p,v,P,定义Za(x)={p: H(x,p)≤a},ZPa(x)=Za(x)-P,σa(x,v)=σZa(x)(v), σPa(x,v)=σZPa(x)(v)。 对于给定的a∈R,P∈RN,对任一x∈TN,ZPa(x)≠Ø。一个连续函数u为方程H(x,P+Du)=a的一个黏性下解当且仅当d#(Dφ(x),ZPa(x))≤0,对任意x∈TN,任意C1上切线φ成立,连续函数u为方程H(x,P+Du)=a的一个黏性上解当且仅当 d#(Dφ(x),ZPa(x))≥0,对任意x∈TN,任意C1下切线φ成立。 黏性下解的2个基本性质: (1)一族黏性下解的上确界仍为黏性下解; (2)若方程H(x,P+Du)=an,an→a的一列黏性下解un一致收敛于某个函数u,则u为方程H(x,P+Du) =a的一个黏性下解。 关于黏性解的基本知识可见Crandall,Evans,Lions[5],Bardi,Capuzzo-Dolcetta[6]。 定理1 假设Hamilton函数H满足条件(H1)-(H4),则存在唯一的a∈R使得方程 存在全局黏性解,记此唯一的a∈R为H(P),且 H(P)=inf{a:方程H(x,P+Du)=a存在黏性下解}。为证明此定理,先证明几个引理。 引理1 Hamilton-Jacobi方程(1)的任一黏性下解uL-ipschitz连续。 证明 固定x∈TN,考虑函数φ(y)=u(y)-C|y-x|,其中C>0为一待定常数。由函数φ的连续性及TN的紧性,存在y∈TN使得函数φ(y)取得最大值,即φ(y)=。断言当C>0充分大时,y =x。假若y≠x,则由于u为方程(1)的黏性下解,而函数y→C|y-x|在y=y≠x处可微,由黏性下解的定义,有 当C>0充分大(不依赖于点x的选择)时,上式与Hamilton函数H的强制性矛盾。因此,当C充分大时,y=x。于是,u(y)-C|y-x|≤u(y)-C(y)-x=u(x),∀y∈TN。 交换x与y的位置,即得|u(x)-u(y)|≤C|y-x|。证毕。 注2 由上述证明过程可知,Hamilton-Jacobi方程(1)的一族黏性下解是等度Lipschitz连续的。上述证明思想来自Bardi和Capuzzo-Dolcetta[6]。 引理2 若当a=a1时,Hamilton-Jacobi方程(1)存在黏性下解u,当a=a2时,Hamilton-Jacobi方程(1)存在黏性上解v,则a1≥a2。 证明 用uδ表示函数u的光滑化,ζδ表示标准的C∞光滑化子。由有向距离d#(·,ZPa1(x))的凸性,利用Jensen不等式,有 因此,对于任意给定的ε>0可以选取δ>0,使得C∞函数uδ满足 若x0为v-uδ的一个最小值点,则uδ为v在点x0的1条下切线。由v为方程(1)的1个上解,可知下式成立: 由(2)(3)可得,a2≤a1+ε。再由ε>0的任意性,可知a1≥a2。证毕。 由上述引理可知,唯一可能使得Hamilton-Jacobi方程H(x,P+Du)=a存在黏性解的a∈R为H(P)= inf{a:方程H(x,P+Du)=a存在黏性下解}。下面将证明对于此唯一的H(P)∈R,方程 确实存在黏性解。 引理3 给定y∈TN,定义 wy(x)=sup{u(x):u(x)为方程(4)的下解且u(y)= 0},则wy(x)在TN上为方程(4)的黏性下解,在TN {y}上为方程(4)的黏性解。 证明 首先说明wy(x)的定义的合理性。只需说明方程(4)的下解的集合非空即可。 利用黏性下解的基本性质(1)可知wy为方程H(x,P+Du)=H(P)的1个黏性下解,故只需再证明wy(x)在TN{y}上为方程(4)的黏性上解即可。 类似于引理3中Ψy(x)的构造,用φy代替φ,选取适当的ε>0和r>0,可以找到方程(4)的1个黏性下解uy,使得uy在某个球B(y,r)内为C1的,且 利用TN的紧性,选取TN的1个有限覆盖Byi,i=1,2,…,n。 这表明u为方程H(x,P+Du)=H(P)的一个严格黏性下解,与H(P)的定义矛盾。证毕。 注3 上述定理的证明表明,方程H(x,P+Du)= H(P)必定有形如 wy(x)=sup{u(x):u(x)为方程(4)的下解且u(y)=0}的黏性解。确定哪些y使得wy(x)为方程的黏性解是一件很有意义的事。Fathi和Siconolfi[2]证明了当且仅当y∈A,A为投影Aubry集时,wy(x)为方程的黏性解。 定理1的证明 由定理2可知存在性成立,由H(P)的表示式 H(P)=inf{a:方程H(x,P+Du)=a存在黏性下解}知唯一性成立。证毕。 推论 H(P)关于P连续。 证明 由H(P)=inf{a:方程H(x,P+Du)=a存在黏性下解}及H(x,p)的连续性即可得到。证毕。 Lions,Papanicolaou和Varadhan还证明了如下结果:若对a∈R,方程H(x,P+Du)=a存在黏性下解,则a≥H(P);若方程H(x,P+Du)=a存在黏性上解,则a≤H (P)。事实上,上述命题的逆命题也是成立的,并且有如下更强的结果。 由此命题,可以得到如下的H(P)的表示式: 定理3 H(P)=inf{a:方程H(x,P+Du)=a存在黏 性下解}= sup{a:方程H(x,P+Du)=a存在黏性上解}= inf{a:方程H(x,P+Du)=a存在严格黏性下解}= sup{a:方程H(x,P+Du)=a存在严格黏性上解}= inf{a:方程H(x,P+Du)=a存在光滑下解}。 由引理2的证明过程可知,若u为方程H(x,P+Du)=a的黏性下解,则uδ为方程H(x,P+Du)=a+ ε的黏性下解,因此若u为方程H(x,P+Du)=a的严格黏性下解,则uδ为方程H(x,P+Du)=a的黏性下解。由H(P)的第三个表达式可知最后一个表达式成立。证毕。 注4 由于黏性上解不一定Lipschitz连续,从而不能保证几乎处处可微,因此引理2的证明对于黏性上解不适用。 注5 关于在更强的条件下,H(P)的更多的性质及更多的表达式可见Evans和Gomes[7],Evans[8-9]。 [1] Evans L C.Weak KAM Theory and Partial Differential Equations.//Dacorogna B,Marcellini P Eds.Calculus of Variations and Nonlinear Partial Differential Equations[C].Berlin:Springer-Verlag,2008:123-154. [2] Fathi A,Siconolfi A.PDE aspects of Aubry-Mather theory for quasiconvex Hamiltonians[J].Calculus of Variations and PDE, 2005,22(2):185-228. [3] Fathi A.Theoreme KAM faible et theorie de Mather sur les systemes lagrangiens[J].C R Acad Paris Sr I Math,1997,324(9): 1043-1046. [4] Evans L C.Periodic homogenization of certain fully nonlinear partial differential equations[J].Proc Roy Soc Edinburgh Sect A, 1992,120(3-4):245-265. [5] Crandall M G,Evans L C,Lions P L.Some Properties of Viscosity Solutions of Hamilton-Jacobi equations[J].Trans Amer Math Soc,1984,282(2):487-502. [6] Bardi M,Capuzzo-Dolcetta I.Optimal control and viscosity solutionsof Hamilton-Jacobi-Bellman equations[M].Boston:Birkhäuser, 1997. [7] Evans L C,Gomes D.Effective Hamiltonians and averaging for Hamiltonian dynamics I[J].Arch Rational Mech Anal,2001, 157(1):1-33. [8] Evans L C.Some new PDE methods for weak KAM theory[J]. Calculus of Variations and PDE,2003,17(2):159-177. [9] Evans L C.A survey of partial differential equations methods in weak KAM theory[J].Comm Pure Appl Math,2004,57(4): 445-480. Abstract: Following the approach of Fathi and Siconolfi we present a geometric proof of existence and uniqueness of effective Hamiltonians of quasiconvex Hamilton-Jacobi equations.Five expressions of the effective Hamiltonian function were also given. Key words: quasiconvex Hamiltonians;effective Hamiltonian;Hamilton-Jacobi equations;viscosity solutions AMS Subject Classifications: 35B27,35B40 责任编辑 朱宝象 A Geometric Proof of Existence and Uniqueness of Effective Hamiltonians of Quasiconvex Hamilton-Jacobi Equations QIAO Yuan-Bo,PIAO Da-Xiong O179.29 A 1672-5174(2010)09Ⅱ-226-04 2009-09-15; 2010-05-25 乔元波(1985-),男,硕士生。E-mail:qiao_yuanbo@126.com2 定理及其证明
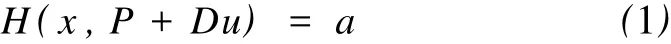
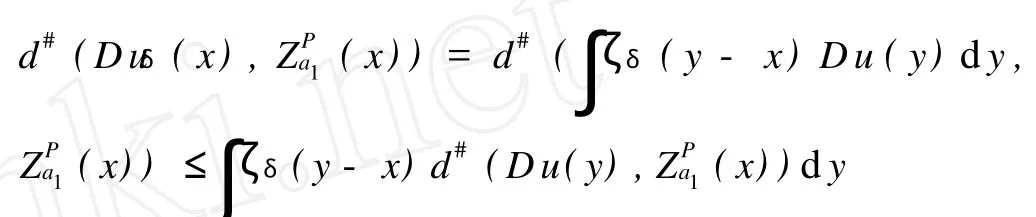

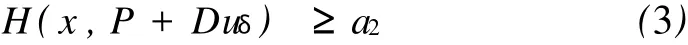
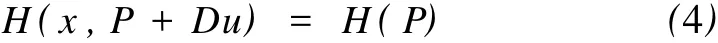

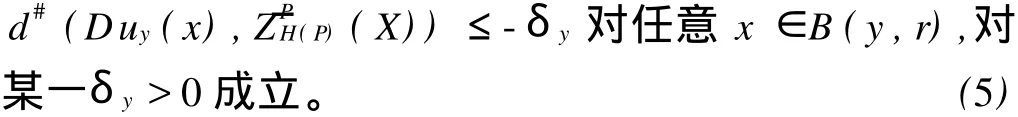



(School of Mathematical Sciences,Ocean University of China,Qingdao 266100,China)
