基于双层隔振的船用空压机系统振动建模研究

金丽琼，邢志胜，朱宝庆，崔冬，李国强

(合肥通用机械研究院有限公司，安徽 合肥 230031)

空气压缩机(以下简称空压机)是现代船舶工业中的重要关键设备之一，目前船用空压机多采用往复活塞式，由于不平衡惯性力等因素的影响，往复活塞式空压机在工作时会产生振动和噪声，影响船舶的隐身性和舒适性，同时，复杂的海况等因素会通过船体反作用于空压机，使空压机的工作环境更加恶劣，很容易造成空压机的损坏。

针对前述问题，通常在船用空压机和甲板之间设计有单层隔振装置或双层隔振装置(包括浮筏隔振装置)，隔振装置一方面能最大限度地隔离空压机的振动沿机座向船体的传递，从而抑制船舱工作室噪声和水下辐射噪声，以达到提高船舶隐身性和舒适性的功能；一方面能有效地抑制外界干扰(如恶劣海况等)通过机座对船舶空压机设备的冲击，以提高空压机的使用寿命。因此，针对隔振结构的船用空压机系统动力学行为的研究受到了广泛的关注。俞微等以船用浮筏隔振系统为研究对象，实例验证了多层隔振系统的稳定性计算方法及通用程序。鲁克明等建立了某艇用空压机双层隔振系统模型，并对其进行了参数及结构优化分析。杜奎等运用导纳原理推导了双层减振装置隔振器对齐安装和不对齐安装方案的传递功率流，发现由于结构传递导纳小于输入导纳，不对齐安装更有利于降低宽频率振动的传递。祝华等采用试验方法研究了隔振器安装位置的偏差对隔振效果的影响，发现隔振器安装位置偏差的变化可以明显影响高频段的隔振效果。尚国清、马永涛等结合舰船设备的减振降噪研究，就浮筏系统的动力学建模分析展开了深入的讨论，全面分析了浮筏系统的多刚体动力学建模法、有限元法、阻抗综合法、模态阻抗法综合法等建模方法，阐述了各种建模方法的特点。

本文在上述研究的基础上，结合工程应用，以基于双层隔振结构的船用空压机为研究对象，将空压机和隔振块简化为刚体，中间的减振块简化为弹簧阻尼系统进行研究，采用Newton 法建立了基于双层隔振的船用空压机系统振动模型，为船用空压机系统的动态特性分析、优化设计以及振动控制等方面提供了较为可靠的工具和理论依据。

1 基于双层隔振结构的船用空压机振动模型

双层结构的船用空压机动力系统主要由船用空压机、减振块、中间质量块等部分组成，如图1。在双层隔振结构的船用空压机系统中，为保证空压机的正常运行，空压机和中间质量块通常都具有较高的强度和刚度，且相对于其结构尺寸来说，空压机和中间质量块在振动过程中的自身变形较小，因此，在双层隔振结构的空压机系统中，可将空压机和中间质量块视为刚体来对待。考虑到发生振动时空压机与中间质量块、中间质量块与船体之间相对位移非常小，建模时可将空压机与中间质量块中间质量块与船体之间的减振块视为线性弹簧阻尼系统，如图2。空压机与中间质量块之间安装4个减振块，中间质量块与船体之间安装有6 个减振块。

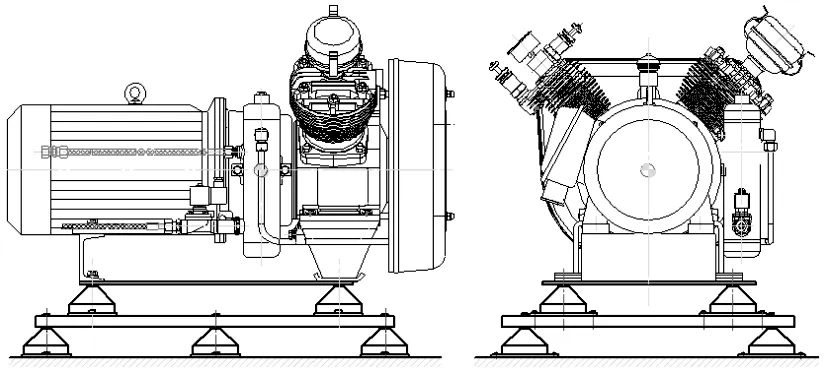
图1 某型船用空压机

图2 隔振结构的空压机振动模型

在图2 中，OXYZ 是位于船体的绝对坐标系，OcXcYcZc是以空压机质心Oc为原点的相对坐标系，OpXpYpZp是以中间质量块质心Op为原点的相对坐标系。模型中主要包括空压机、减振块、中间质量块以及船体，其中0 处代表空压机往复惯性力等因素的激励位置，1 ～4 处代表空压机与中间质量块连接位置，5 ～10 处代表中间质量块与船体连接位置。本文考虑的基于隔振结构的空压机系统振动模型共有12 个自由度，即将空压机和中间质量块视为2 个具有6 自由度的空间刚体结构(3 个平动和3 个转动)。设空压机的质量为mc，空压机绕坐标轴Xc、Yc和Zc的转动惯量分别为Jcx、Jcy和Jcz，空压机激励源位置以及空压机与减振块连接位置各点的受力可表示为各受力点在坐标系OcXcYcZc中的位置坐标可表示为lic=(lxic,lyic,lzic)T(i=0,1,···,4)，当受力点位置位于坐标轴正向时，其坐标值取正值，当受力点位置位于坐标轴负向时，其坐标值取负值；设中间质量块的质量为mp，中间质量块绕坐标轴Xp、Yp和Zp的转动惯量分别为Jpx、Jpy和Jpz，中间质量块上各作用点的受力可表示为Fip=(Fxip,Fyip,Fzip)T，各受力点在坐标系OpXpYpZp中的位置坐标可表示为lip=(lxip,lyip,lzip)T(i=1,2,···,10)，当受力点位置位于坐标轴正向时，其坐标值取正值，当受力点位置位于坐标轴负向时，其坐标值取负值。点1 ～4 处减振块的刚度和阻尼矩阵均可分别表示为kic=diag(kxic,kyic,kzic)和cic=diag(cxic,cyic,czic)； 点5 ～10 处 减 振 块 的 刚 度和阻尼矩阵均可分别表示为kip=diag(kxip,kyip,kzip) 和以系统的静平衡位置作为初始状态假设中间质量块在外力Fip的作用下发生的位置变化可表示为Xp=(xp,yp,zp,θpx,θpy,θpz)T，则可推导出中间质量块的6 自由度振动微分方程的矩阵表达式

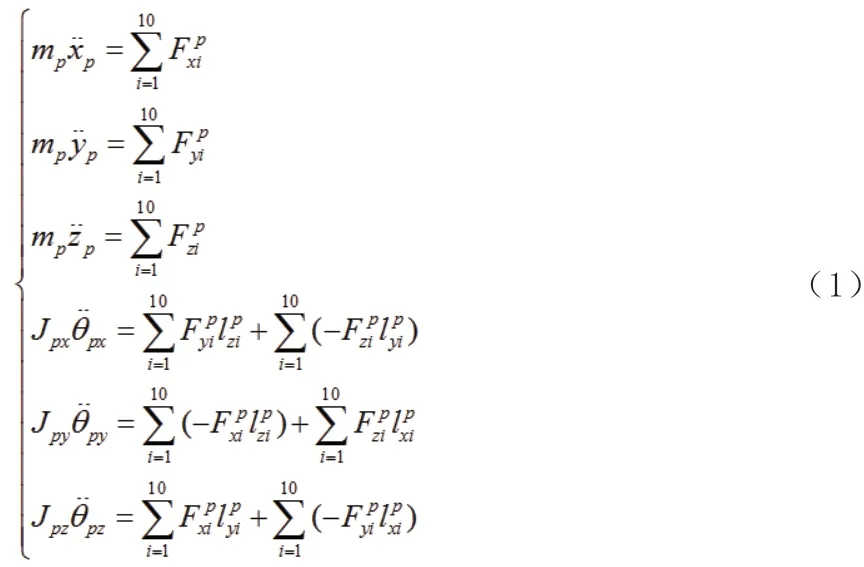
式（1）中减振块耦合点处作用力的力矩正负号是由于作用力和耦合点处的坐标来共同确定的。式（1）可用矩阵形式表示如下：

并且有

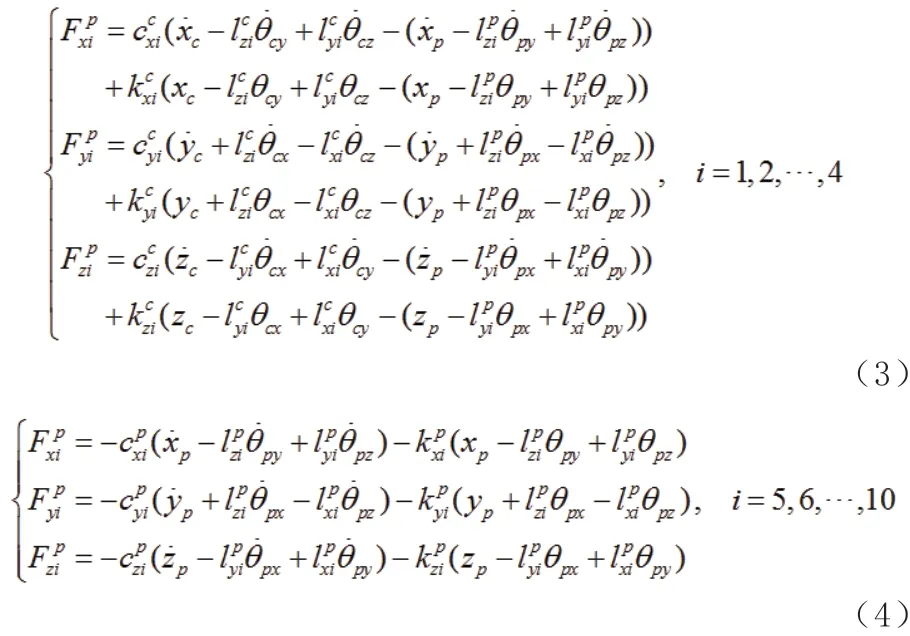
将式(3)和式(4)写成矩阵形式得

将式(2)和式(7)合并可写为：

将式(5)和式(6)代入式(8)，并整理得

式中各元素表达式为：

2 模型有效性分析

方程（9）的结构形式与严济宽等在文献[14]和周世雄等在文献[15]中提出的双层隔振模型相似。在该模型（9）的基础上，如果仅考虑空压机和中间质量块在垂直方向上的两个自由度，则模型（10）可简化为：

此时，得到的空压机系统振动模型与文献[9]和[16]曾经提出的船用空压机系统振动模型是一致的；如果模型（10）中仅考虑单层隔振的作用，忽略中间质量块和减振块阻尼特性的影响，且仅考虑空压机系统的自由振动，则模型（10）可简化为：

式中各元素表达式为：

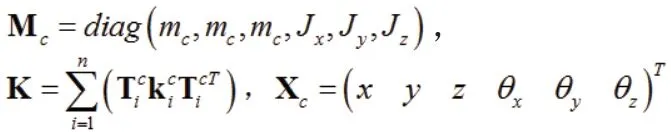
其中刚度矩阵K 中的n 代表空压机与船体之间减振块的数量。此时，得到的空压机系统振动模型与文献[3]描述船用空压机6 自由度刚体模型一致的；由此可以看出，本文提出的基于双层隔振系统的空压机振动模型在设定条件下可以推导出上述文献中的研究模型，因此本文提出的振动模型具有较强的适用性和通用性。

3 结语

（1）考虑空压机和中间质量块的耦合作用，将双层隔振结构的空压机振动系统简化为12 个自由度，使整个模型可以考虑的因素更多，更接近实际情况，模型的通用性更强。

（2）与以往的有效模型进行了比较，比较结果表明本文提出的12 自由度模型考虑的因素更多，形式更通用。

（3）在对船用空压机振动特性进行分析时，不仅要建立其数学模型，还需要考虑空压机不平衡惯性力等因素的影响，同时还要考虑海况等复杂外部因素的影响，本文仅对双层隔振结构的船用空压机系统的数学模型进行了研究和分析，而对空压机不平衡惯性力以及海况等复杂因素对整个系统的动态响应分析将在后续工作中进行完善，从而实现对船用空压机系统动力学的完整分析。