磁通反向永磁电机的定子绕组电阻不平衡故障程度定量估算研究

丁石川 童琛 杭俊 王群京

摘 要：针对定子绕组电阻不平衡（SWRI）故障检测和故障程度估算问题，提出一种基于零序电压（ZSVC）和定子电流的磁通反向永磁（FRPM）电机的定子绕组电阻不平衡故障程度估算方法，有助于安排合理的维修计划。首先，利用零序电压和定子电流与附加电阻的关系，建立关于附加电阻的二元二次方程组;然后，通过求解二元二次方程组得到附加电阻值，并利用得到的附加电阻值实现定子绕组电阻不平衡故障程度估算;最后，在磁通反向永磁电机仿真和实验平台上进行算法验证，仿真和实验结果表明了所提出的故障程度估算方法的有效性和鲁棒性。

关键词：磁通反向永磁电机;定子绕组电阻不平衡;故障程度;零序电压

中图分类号：TM 46

文献标志码：A

文章编号：1007-449X（2019）07-0079-08

Abstract：Aiming at solving the problem of stator winding resistance imbalance （SWRI） fault detection and fault severity estimation， a SWRI fault severity estimation method based on zero sequence voltage component （ZSVC） and stator currents was proposed for fluxreversal permanent magnet （FRPM） machine， which can help in determining the scheduled maintenance. Firstly， a binary linear equation group about the additional resistances was estimated based on the relationship between the ZSVC， stator currents and the additional resistances. Secondly， by solving the binary linear equation group， the additional resistances were calculated， and the SWRI fault severity was estimated by the calculated additional resistances. Finally， the proposed method was verified on the simulation and experimental platform of FRPM machine. Both the simulation and experimental results show the effectiveness and robustness of the proposed fault severity estimation method.

Keywords：fluxreversal permanent magnet machine; stator winding resistance imbalance; fault severity; zero sequence voltage

0 引 言

傳统的永磁电机通常将永磁体安装在转子上，为了防止高速运行时磁钢受到离心力的影响而甩落，在转子上装有不锈钢或金属纤维材料制作的固定装置。但是这样会引起散热困难，而温升会导致钕铁硼（NdFeB）为主的永磁体性能下降，严重时甚至发生不可逆退磁，这也限制了普通转子永磁型电机在某些场合的应用。磁通反向永磁（fluxreversal permanent magnet，FRPM）电机是一种新型结构的定子永磁型电机，它克服了传统转子型永磁电机的诸多缺点，具有较好的应用前景[1]。

对于磁通反向永磁电机，常见的故障类型与传统转子型永磁电机是一样的，大致可以分为以下3类：电气故障（定子绕组）、机械故障（轴承）和永磁体故障（永磁体损坏或退磁）[2-4]。其中，定子绕组电阻不平衡是一种常见的电气故障[4]。定子绕组电阻不平衡指的是由于定子绕组的电阻值增加而导致的不平衡故障。这种故障可能是由于加工工艺低劣、热循环和振动等因素综合造成的，也有可能是由于接线端口的损坏（腐蚀或污染）造成的[5]。该故障会导致定子电压或电流的不平衡、转矩脉动的增加、平均转矩的降低、损耗和热量的增加等。当早期的定子绕组电阻不平衡故障发生时，电机仍可继续运行，但若不能及时检测而导致故障严重程度加剧时，将会导致定子绕组温度升高，最终会破坏定子绕组的绝缘，进而引起短路故障，甚至对整个电机系统造成破坏。因此，研究定子绕组电阻不平衡故障对提高磁通反向永磁电机的可靠性具有重要的意义。

自从1996年R.P.Deodhar等[6]首次提出FRPM电机以来，已经取得了一系列有价值的研究成果。然而，目前研究成果均集中在FRPM电机的电磁静态特性分析[7-9]、本体设计和优化设计[10-16]以及控制[17-18]等方面，而对该类型电机的故障诊断相关研究的报道很少，更不用提定子绕组电阻不平衡故障。目前，关于永磁电机的定子绕组电阻不平衡故障，主要集中在转子永磁型电机和磁通切换型永磁电机。文献[19]利用定子电流和零序电压实现永磁电机的定子绕组电阻不平衡故障诊断，但是不能判断出故障相，并且只讨论了单相绕组发生故障。文献[20]利用改进的故障特征量和角度差分别实现定子绕组电阻不平衡故障的诊断和定位，并且讨论了多相绕组发生故障，但是不能估算每相故障绕组的故障程度，尤其是在多相绕组发生故障的情况下。文献[21-22]提出利用零序电压诊断九相磁通切换型永磁电机的定子绕组电阻不平衡故障，但不能判断故障相的故障程度，尤其故障发生在多相定子绕组。

基于上述情况，在文献[20]研究基础上进一步地研究，提出了基于零序电压和定子电流的FRPM电机定子绕组电阻不平衡故障程度定量估算方法，能有效地估算故障相的故障程度，克服了文献[20]中的不足（不能估算每相故障绕组的故障程度），有助于安排合理的维修计划。首先，介绍了三相FRPM电机的拓扑结构，并通过有限元仿真结果，对FRPM电机的空载反电动势进行谐波分析;其次，从理论上分析了定子绕组电阻不平衡故障对零序电压的影响，并建立零序电压与定子电流和定子绕组电阻不平衡之间的关系;接着，通过求解二元二次方程组计算故障相增加的电阻值，进而实现故障相故障程度的估算;最后，对所提出的故障程度定量估算方法进行仿真和实验验证。研究表明，所提出的故障程度定量估算方法能有效地实现定子绕组电阻不平衡故障程度估算。

1 FRPM电机

1.1 FRPM电机本体

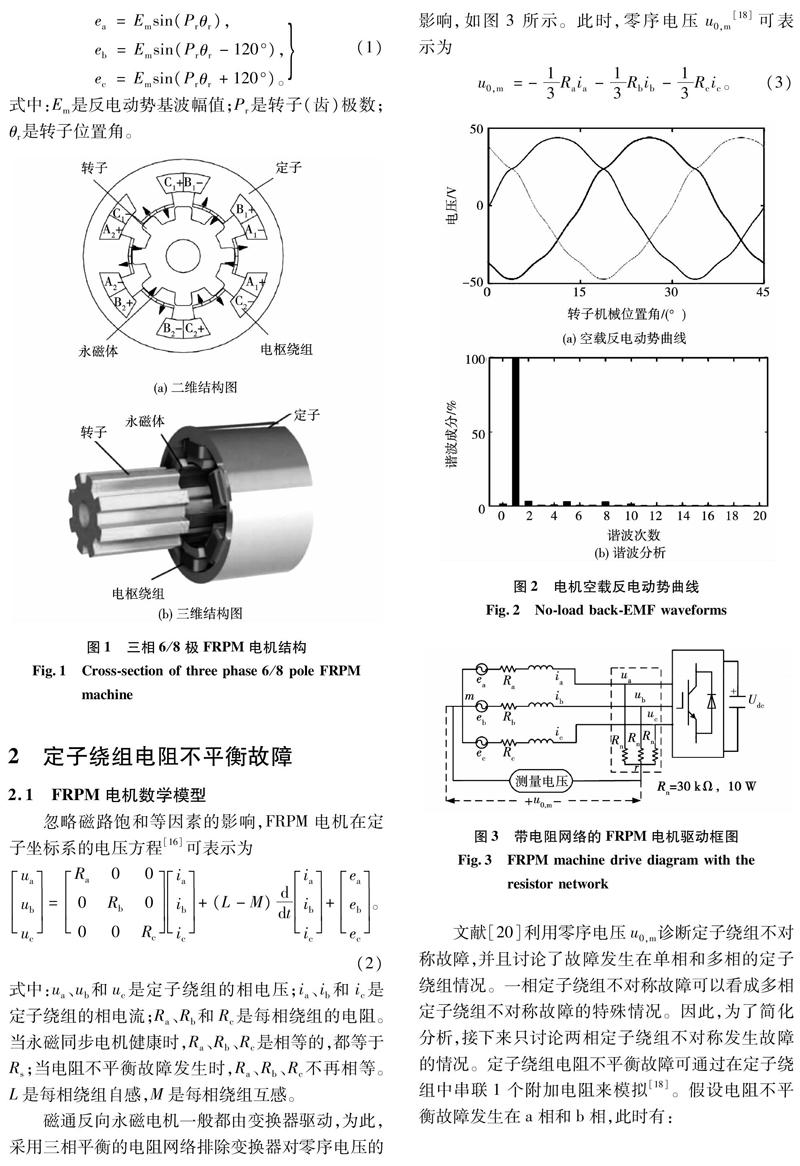
图1为1台三相6/8极FRPM电机的拓扑结构，其定转子呈双凸极结构，转子上既无绕组也无永磁体，结构非常简单，在定子上设置了绕组和永磁体[14]。每个定子槽中并排布置2个不同相的集中式线圈的2个圈边，6个定子齿上一共套有6个线圈，且分成2组，径向相对的2个线圈组成一相，如图中A1、A2是A相的2个线圈，其余两相以此类推。此外，采用集中绕组大大缩短了端部长度，减少了用铜量和铜耗。转子有8个齿，称为8极，定子永磁型电机转子极数决定了转子周期，即每相空载感应电动势在一个完整的机械周期内（360°）变化8次，对应的电周期为45°。定转子导磁铁心采用硅钢片冲片压叠而成，都呈凸极结构。该结构便于采用模块化制造工艺，集中式绕组线圈可以预先绕制好，直接套在定子齿上，易于提高槽满率，然后再将6个定子齿拼装组成一个定子铁心整体。

1.2 反电动势分析

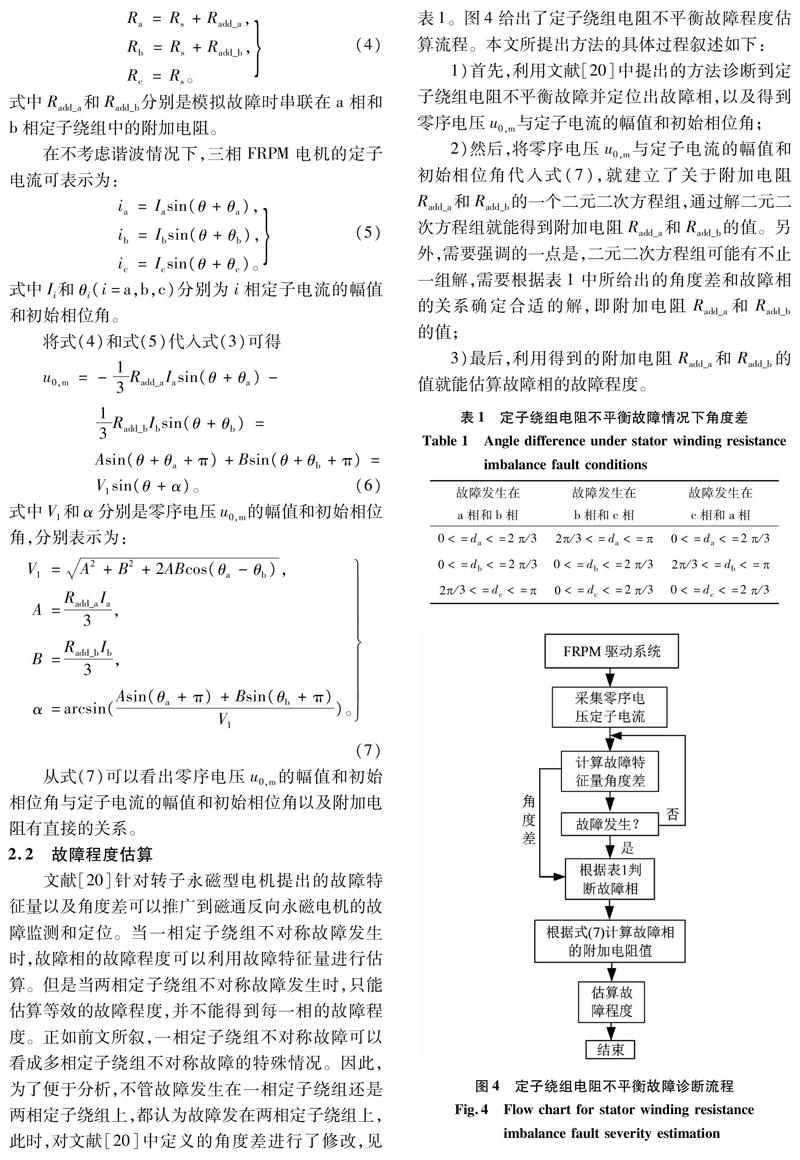
图2为转速500 r/min时FRPM电机有限元仿真的三相空载反电动势波形。可以看出，在电机空载反电动势中，谐波的幅值相对于基波的幅值很小，可以忽略。因此，三相空载反电动势可表示为：

2 定子绕组电阻不平衡故障

2.1 FRPM电机数学模型

忽略磁路饱和等因素的影响，FRPM电机在定子坐标系的电压方程[16]可表示为

式中：ua、ub和uc是定子绕组的相电压;ia、ib和ic是定子绕组的相电流;Ra、Rb和Rc是每相绕组的电阻。当永磁同步电机健康时，Ra、Rb、Rc是相等的，都等于Rs;当电阻不平衡故障发生时，Ra、Rb、Rc不再相等。L是每相绕组自感，M是每相绕组互感。

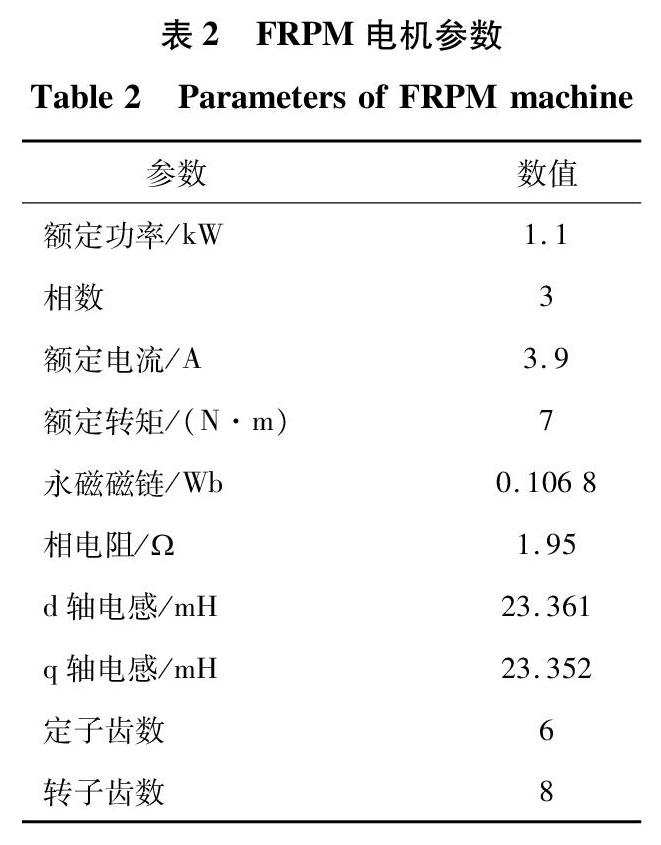
磁通反向永磁电机一般都由变换器驱动，为此，采用三相平衡的电阻网络排除变换器对零序电压的影响，如图3所示。此时，零序电压u0，m[18]可表示为

文献[20]利用零序电压u0，m诊断定子绕组不对称故障，并且讨论了故障发生在单相和多相的定子绕组情况。一相定子绕组不对称故障可以看成多相定子绕组不对称故障的特殊情况。因此，为了简化分析，接下来只讨论两相定子绕组不对称发生故障的情况。定子绕组电阻不平衡故障可通过在定子绕组中串联1个附加电阻来模拟[18]。假设电阻不平衡故障发生在a相和b相，此时有：

式中Radd_a和Radd_b分别是模拟故障时串联在a相和b相定子绕组中的附加电阻。

在不考虑谐波情况下，三相FRPM电机的定子电流可表示为：

从式（7）可以看出零序电压u0，m的幅值和初始相位角与定子电流的幅值和初始相位角以及附加电阻有直接的关系。

2.2 故障程度估算

文献[20]针对转子永磁型电机提出的故障特征量以及角度差可以推广到磁通反向永磁电机的故障监测和定位。当一相定子绕组不对称故障发生时，故障相的故障程度可以利用故障特征量进行估算。但是当两相定子绕组不对称故障发生时，只能估算等效的故障程度，并不能得到每一相的故障程度。正如前文所叙，一相定子绕组不对称故障可以看成多相定子绕组不对称故障的特殊情况。因此，为了便于分析，不管故障发生在一相定子绕组还是两相定子绕组上，都认为故障发在两相定子绕组上，此时，对文献[20]中定义的角度差进行了修改，见表1。图4给出了定子绕组电阻不平衡故障程度估算流程。本文所提出方法的具体过程叙述如下：

1）首先，利用文献[20]中提出的方法诊断到定子绕组电阻不平衡故障并定位出故障相，以及得到零序电压u0，m与定子电流的幅值和初始相位角;

2）然后，将零序电压u0，m与定子電流的幅值和初始相位角代入式（7），就建立了关于附加电阻Radd_a和Radd_b的一个二元二次方程组，通过解二元二次方程组就能得到附加电阻Radd_a和Radd_b的值。另外，需要强调的一点是，二元二次方程组可能有不止一组解，需要根据表1中所给出的角度差和故障相的关系确定合适的解，即附加电阻Radd_a和Radd_b的值;

3）最后，利用得到的附加电阻Radd_a和Radd_b的值就能估算故障相的故障程度。

3 仿真和实验

为了验证提出的故障程度估算方法，进行仿真和实验研究。FRPM电机驱动系统采用id=0的滞环控制方法，故障程度估算算法作为控制系统的一个附加子程序。仿真和实验过程利用的FRPM电机参数见表2。在仿真过程中，FRPM电机的模型根据定子坐标系下电压方程进行搭建。在实验过程中，通过在相绕组中串联附加电阻来模拟定子绕组不对称故障。

3.1 仿真结果

在仿真过程中，设置不同的附加电阻值，即0.1、0.3、0.5、1和2 Ω。表3给出了定子绕组电阻不平衡故障发生在a相和b相的仿真结果，其中FRPM的工作参考转速为600 r/min，负载转矩为3 N·m。从仿真结果可以看出，不管定子绕组电阻不平衡故障发生在一相或两相，计算得到的附加电阻值都接近或等于理论值。因此，仿真结果表明提出的方法可以有效地实现磁通切反向永磁电机的定子绕组电阻不平衡故障程度估算。

为了进一步验证提出方法的性能，在FRPM电机不同的工作点（转速和负载）情况下进行仿真，其中1 Ω附加电阻串联在a相绕组中。表4给出了在不同参考转速情况下的仿真结果（负载为3 N·m）。表5给出了在不同负载情况下的仿真结果（参考转速为600 r/min）。从表4和表5可以看出，在不同的转速和负载情况下，计算得到的附加电阻值都接近或等于理论值。因此，仿真结果表明提出的方法具有很好的鲁棒性能。

3.2 实验结果

为了进一步验证故障诊断方法的有效性，构建了三相FRPM电机驱动系统实验平台，如图5所示，其中1个2.2 kW永磁同步电机通过联轴器与FRPM電机直接连接，作为负载电机。电压和电流利用LEM电流传感器和电压传感器采集，转子位置利用增量式的光电编码器进行采集。控制器采用dSPACE实时仿真单板系统DS1104控制板，与综合设计仿真平台下的MATLAB/Simulink系统及仿真部分连接，通过直接编译Simulink环境下的仿真模型，生成dSPACE实验平台能够辨识的代码，建立起可以在线调整各项参数的实验系统。另外，在实验过程中，通过在定子绕组中串联附加电阻值来模拟定子绕组电阻不平衡故障。另外，由于实验条件的限制，只模拟了2种故障程度（1.2 Ω和2.4 Ω）。

图6给出了三相FRPM电机在正常和故障情况下的实验结果，其中FRPM的工作参考转速为600 r/min，负载转矩为3 N·m;故障情况下，在A相绕组中串入2.4 Ω附加电阻。从图6（a）可以看出，在正常情况下，定子电流ia和ib波形是很正弦的，并且零序电压u0，m的波形接近于0。从图6（b）可以看出，在故障情况下，定子电流ia和ib波形与正常情况下相比，没有明显的变化，但是零序电压u0，m的波形中出现了周期性信号，表明故障对零序电压u0，m的影响很明显。

表6给出了定子绕组电阻不平衡故障发生在a相和b相的实验结果，其中FRPM的工作参考转速为600 r/min，负载转矩为4 N·m。从实验结果可以看出，不管定子绕组电阻不平衡故障发生在一相或两相，计算得到的附加电阻值都接近或等于理论值。因此，实验结果表明提出的方法可以有效地实现磁通反向永磁电机的定子绕组电阻不平衡故障程度估算。

表7给出了在不同参考转速情况下的仿真结果（负载为3 N·m）;表8给出了在不同负载情况下的仿真结果（参考转速为600 r/min），其中1.2 Ω附加电阻串联在a相绕组中。从表7和表8可以看出，在不同的转速和负载情况下，计算得到的附加电阻值都接近或等于理论值。因此，实验结果表明提出的方法具有很好的鲁棒性能。

从上述仿真和实验可以看出，仿真结果和实验结果都接近或等于理论值。因此，两者都表明了提出的方法可以有效地实现磁通反向永磁电机的定子绕组电阻不平衡故障程度估算。

4 结 论

本文在分析了定子绕组电阻不平衡故障对零序电压影响的基础上，提出基于零序电压和定子电流的三相FRPM电机定子绕组电阻不平衡故障程度估算方法。仿真和实验结果验证了提出方法的有效性，并得到以下结论：

1）利用零序电压和定子电流的关系可以有效地估算出附加电阻值，进而实现故障程度的估算;

2）提出的故障方法不受转速和负载变化的影响，具有很好的鲁棒性;

3）本文仅以FRPM电机为例进行了分析，本文提出的方法具有一定的通用性，可以推广到转子永磁型电机以及其它结构的定子永磁型电机，如磁通切换型永磁电机等。

参 考 文 献：

[1] CHENG Ming， HUA Wei， ZHANG Jianzhong， et al.Overview of statorpermanent magnet brushless machines[J]. IEEE Transactions on Industrial Electronics， 2011， 58（1）： 5087.

[2] 何静，张昌凡，贾林，等.一种永磁同步电机的失磁故障重构方法研究[J] .电机与控制学报，2014，18（2）：8.

HE Jing，ZHANG Changfan，JIA Lin，et al. Demagnetization fault reconstruction for permanent magnet synchronous motor[J] .Electric Machines and Control，2014，18（2）：8.

[3] 赵洪森，戈宝军，陶大军，等.同步发电机定子绕组匝间短路故障诊断研究[J] .哈尔滨理工大学学报，2018，23（1）：99.

ZHAO Hongsen，GE Baojun，TAO Dajun，et al. Investigation on stator winding interturns short circuit fault diagnosis[J].Journal of Harbin University of Science and Technology，2018，23（1）：99.

[4] CHENG Ming， HANG Jun， ZHANG Jianzhong. Overview of fault diagnosis theory and method for permanent magnet machine [J]. Chinese Journal of Electrical Engineering， 2015， 1（1）： 21.

[5] YUN J， CHO J， LEE S B， et al. Online detection of highresistance connections in the incoming electrical circuit for induction motors[J]. IEEE Transactions on Industry Applications， 2009， 45（2）： 694.

[6] DEODHAR R P， ANDERSSON S， BOLDE I， et al. The fluxreversal machine： a new brushless doublysalient permanentmagnet machine[J].IEEE Transactions on Industry Applications， 1997，33（4）： 925.

[7] 楊玉波， 王秀和， 张宗盛，等. 磁通反向式永磁电机性能计算与转矩脉动削弱措施研究[J].中国电机工程学报， 2015， 35（11）： 2838.

YANG Yubo， WANG Xiuhe， ZHANG Zongsheng， et al. The performance analytical calculation and the torque ripple reduction methods of flux reversal machine[J]. Proceedings of the CSEE， 2015， 35（11）： 2838.

[8] MORE D S，FERNANDES B G. Power density improvement of three phase flux reversal machine with distributed winding[J]. IET Electric Power Application， 2010， 4（2）： 109.

[9] KIM T H， WON S H， BONG K， et al. Reduction of cogging torque in fluxreversal machine by rotor teeth pairing[J]. IEEE Transactions on Magnetics， 2005， 41（10）： 3964.

[10] KIM T H. A study on the design of an inset permanentmagnettype fluxreversal machine[J]. IEEE Transactions on Magnetics， 2009， 45（6）： 2859.

[11] MORE D S，FERNANDES B G. Novel three phase flux reversal machine with full pitch winding[C]//7th International Conference on Power Electronics，October 22-26，2007，Daegu， South Korea. 2007：1007-1012.

[12] HUA Wei， WU Zhongze， CHENG Ming. A novel threephase fluxreversal permanent magnet machine with compensatory windings[C]//International Conference on Electrical Machines and Systems，October 10-13，2010，Incheon，South Korea.2010： 1117-1121.

[13] KIM T H， LEE J. A study of the design for the flux reversal machine[J].IEEE Transactions on Magnetics，2004，40（4）：2053.

[14] ZHAO Wenxiang，JI Jinghua， LIU Guohai， et al. Design and analysis of a new modular linear fluxreversal permanentmagnet motor[J]. IEEE Transactions on Applied Superconductivity， 2014， 24（3）： 1.

[15] GAO Yuting， QU Ronghai， LI Dawei， et al. Consequentpole fluxreversal permanentmagnet machine for electric vehicle propulsion[J]. IEEE Transactions on Applied Superconductivity， 2016， 26（4）： 1.

[16] 施铭.新型双极性定子表面贴装式永磁电机设计与分析[D]. 南京：东南大学，2014.

[17] HUA Wei， HUANG Wentao， YU Feng. Improved modelpredictivefluxcontrol strategy for threephase fourswitch inverterfed fluxreversal permanent magnet machine drives[J]. IET Electric Power Application， 2017， 11（5）： 717.

[18] 赵文祥， 刘虎， 吉敬华，等. 城轨交通用磁通反向永磁直线电机的垂向力控制[J]. 电机与控制应用， 2016， 40（12）： 29.

ZHAO Wenxiang， LIU Hu， JI Jinghua， et al. Control of vertical force in fluxreversal permanent magnet linear motor for urban rail transit applications[J]. Electric Machines and Control Application， 2016， 40（12）： 29.

[19] URRESTY J C，RIBA J R，ROMERALR L，et al.Mixed resistive unbalance and winding interturn faults model of permanent magnet synchronous motors[J].Electrical Engineering，2015，97（1）：75.

[20] ZHANG Jianzhong， HANG Jun， DING Shichuan， et al. Online diagnosis and localization of highresistance connection in PMSM with improved fault indicator[J]. IEEE Transactions on Power Electronics， 2017， 32（5）： 3585.

[21] HANG Jun， ZHANG Jianzhong， DING Shichuan， et al. Fault diagnosis of highresistance connection in ninephase fluxswitching permanent magnet machine considering neutralpoint connection model[J]. IEEE Transactions on Power Electronics， 2017， 32（85）：6444.

[22] HANG Jun，ZHANG Jianzhong， CHENG Ming， et al. Fault diagnosis of highresistance connection in ninephase fluxswitching permanent magnet machine[C]//18th International Conference on Electrical Machines and Systems， October 25-28， 2015， Pattaya， Thailand. 2015： 1691-1696.

（編辑：邱赫男）