考虑输出电压平衡的三相四开关逆变器SVPWM过调制策略

李泽 郭源博 张铭 张晓华

摘 要：针对三相四开关逆变器（TPFSI）电压输出能力受限，且传统过调制方法存在输出三相电压基波幅值不平衡的问题，提出一种考虑输出电压平衡的空间矢量脉宽调制过调制算法。首先，推导三相四开关逆变器输出平衡三相电压的约束条件;然后，根据调制比的大小，将过调制区域分为三部分，即过调制Ι区、过调制II区和过调制III区，并基于叠加定理分别选择用于矢量合成的电压矢量和加权系数，合成期望的电压矢量;最后，对传统的过调制算法与提出的基于叠加定理的过调制算法进行仿真研究和实验验证。结果表明：与传统的三相四开关逆变器过调制算法相比，所提出的过调制算法能够输出平衡的三相电压，且基波幅值与调制比呈线性关系，同时避免了控制角和保持角的在线计算或离线存储，具有易于数字化实现的优点。

关键词：三相四开关逆变器;三相输出电压平衡;叠加定理;空间矢量脉宽调制;过调制

中图分类号：TM 46

文献标志码：A

文章编号：1007-449X（2019）07-0053-10

Abstract：The ability of voltage output for threephase fourswitch inverter （TPFSI） is limited， and the problem of threephase fundamental voltage unbalance exists in traditional overmodulation strategy. As a result， an overmodulation algorithm of TPFSI for balanced output voltages was proposed. Firstly， the constraint condition for TPFSI outputting balanced threephase voltages was derived. Then， according to the value of the modulation index， the overmodulation region is divided into three parts， namely overmodulation region I， overmodulation region II， and overmodulation region III. Next， the voltage vectors and the corresponding weighting coefficients were chosen to synthesis the reference voltage vector. Finally， the output voltage performance of the TPFSI using traditional overmodulation algorithm and the proposed overmodulation algorithm was simulated and validated， respectively. The results show that compared with traditional overmodulation algorithm， the proposed overmodulation algorithm based on superposition principle can output the balanced threephase voltages， and the fundamental component of the output voltage is proportional to the modulation index. Meanwhile， the proposed algorithm can be easily digitally realized without online calculation or offline storage for the control angles and holding angles.

Keywords：threephase fourswitch inverter; balanced threephase output voltages; superposition principle; space vector pulse width modulation; overmodulation

0 引 言

電压型逆变器由于其结构简单、控制灵活等优点，已广泛应用于工业、交通、航空和军事等重要领域[1-2]。然而，由于IGBT等功率开关器件易发生开路或短路故障，导致逆变器无法正常工作。因此，为获得更高的可靠性，通常要求系统发生故障时，仍旧能够继续运行，即系统具有容错能力[3]。为满足这一需求，可对传统三相六开关逆变器在某相桥臂发生故障后的拓扑重构为三相四开关逆变器（threephase fourswitch inverter， TPFSI）。然而，三相四开关逆变器仅有两相桥臂，只能输出4种开关状态，即只有4个有效电压矢量且没有零矢量产生，因此其调制算法有别于三相六开关逆变器，需要重新设计[4-7]。

三相四开关逆变器在线性调制区域的调制算法，已有较多的学者进行了详细的研究[8-13]。然而，对于三相四开关逆变器，其能够输出的最大线性调制比只有三相六开关逆变器的一半。因此，为提高直流电压利用率，增强逆变器的输出能力，增大电机稳定运行区域，通常采用过调制策略[14-16]。

目前国内外三相四开关逆变器过调制策略的研究成果较少，文献[5]提出了一种具有很好理论研究价值的过调制策略，即按照调制比的大小将过调制区域划分为过调制I区、过调制II区和过调制III区，通过在过调制I区和过调制II区计算控制角，在过调制III区计算保持角来确定补偿电压矢量的幅值和相位。这种方法可一定程度上提高直流电压利用率，但其需要建立控制角、保持角与调制比的关系，通过在线计算繁琐的三角函数或查表的方式来实现，限制了算法的执行速度或精度;另一方面，采用该方法在整个过调制区域均存在着实际输出三相电压不平衡的问题，这将导致在改善系统性能上仍有很大的局限性，限制了该算法的实际应用。文献[9]提出了一种基于等效三相六开关逆变器的调制策略，采用4个有效电压矢量合成等效于六开关逆变器的6个虚拟电压矢量，然后根据六开关的调制方式来设计三相四开关逆变器线性调制区域的调制策略，然而没有具体给出过调制策略。文献[11]从载波调制角度，给出了过调制区域的调制算法，将整个过调制区域作为一个整体来控制，易于数字化实现，然而该算法输出脉冲的谐波和直流电压利用率不理想，需要进一步改善。

本文首先给出三相四开关逆变器拓扑结构及其空间电压矢量调制策略;然后针对传统基于空间电压矢量脉宽调制（space vector pulse width modulation，SVPWM）过调制策略输出电压不平衡的问题，推导出可实现输出三相电压平衡的调制策略约束条件，在此基础上，针对传统过调制算法依赖控制角与保持角复杂计算的问题，提出一种基于叠加定理的过调制策略。最后，对传统过调制策略和所提过调制策略进行仿真验证和实验对比。

1 三相四开关逆变器的拓扑及空间电压矢量调制策略

1.1 三相四开关逆变器的拓扑结构

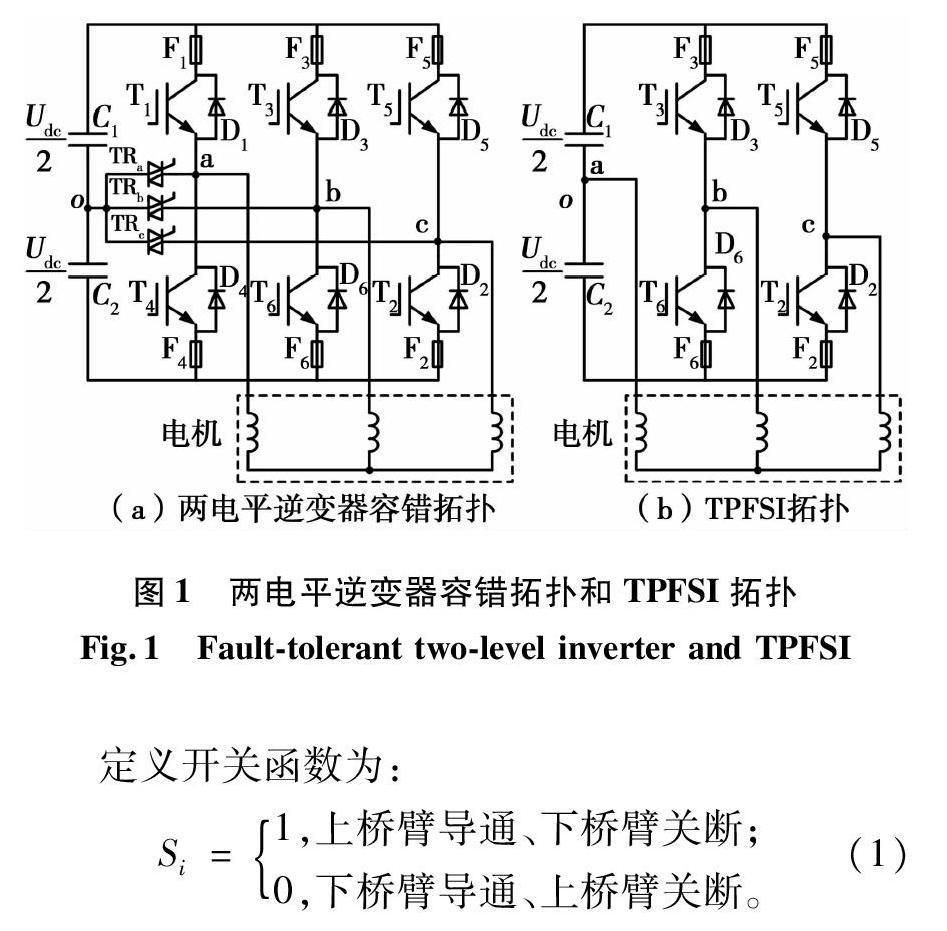
两电平逆变器容错拓扑如图1（a）所示，以a相桥臂功率开关器件发生故障为例，通过快速熔丝F1、F4将故障桥臂切除，同时打开双向晶闸管TRa，从而将容错拓扑重构为三相四开关逆变器，如图1（b）所示[5-6]。

根据Sb和Sc的不同开关组合，可以得到四种开关状态。联立式（2）、式（3）可知，三相四开关逆变器可以输出4个空间电压矢量，如表1所示。

由表1可知，三相四开关逆变器可以输出4个幅值不等，相位依次相差π/2的有效电压矢量，且没有零矢量的产生。因此，空间电压矢量在α-β平面分布如图2所示。

1.2 三相四开关逆变器SVPWM基本原理

由图2可知，四个空间电压矢量将整个平面分为四个扇区。以第一扇区为例，假设参考电压矢量Ur的相角为θ，借鉴传统三相六开关逆变器SVPWM调制算法，参考电压矢量由相邻的两个有效电压矢量和零电压矢量合成，根据伏秒平衡原理可得

然而，三相四开关逆变器在α-β平面上不存在零电压矢量。文献[1]提出了采用两个幅值相等，相位相反的电压矢量作用相同的时间来获得等效的零电压矢量，借鉴这一思想，采用有效电压矢量U1和U3来等效零电压矢量。因此，在整个复平面内，有效电压矢量的实际作用时间可表示为：

为减小开关频率，降低开关损耗和抑制谐波，开关模式需满足：1）每次开关状态转换时，只改变其中一相的开关状态;2）前一个采样周期的末状态是下一个采样周期的始状态。因此各个扇区的开关模式切换序列如图3所示。

2 基于叠加定理的SVPWM过调制策略

2.1 SVPWM过调制策略基本原理

首先定义调制比[9]为

借鉴文献[5，14]的思想，将三相四开关逆变器的整个运行区域按照调制比m的大小，划分为线性调制区（0

如图2所示，线性调制区域与过调制I区的临界条件为|Ur|等于四边形内切圆半径，根据式（8），临界调制比m1=0.906 9。进入过调制区域后，参考电压矢量超出四边形区域的部分不能实际输出。因此，需要对参考电压矢量进行调整，以补偿实际超出四边形区域损失的部分。

传统的三相四开关过调制策略采用计算控制角与保持角的方法，即根据实际输出与给定电压基波幅值相等原则，在过调制I区和过调制II区，分别计算控制角αr1和αr2与调制比m的关系，进而计算出对应的补偿电压矢量Uc1和Uc2;在过调制III区，计算保持角αh与调制比m的关系，参考电压矢量相位小于αh时，通过输出电压矢量保持在四边形顶点的方式进一步增大输出电压[5]。

这种方法一定程度上提高了直流电压利用率，但存在着以下两点不足：

1）控制角αr和保持角αh在线计算困难;

2）实际输出的三相电压不平衡。

针对不足1），文献[14]提出了一种基于叠加定理的三相六开关过调制策略，在过调制区域分别选择不同的电压矢量，通过加权合成补偿电压矢量，易于数字化实现。借鉴这一思想，提出了一种基于叠加定理的三相四开关过调制策略。

针对不足2），首先分析了三相四开关逆变器具有4个基本电压矢量幅值不等的特殊性，在此基础上提出了输出平衡三相电压的约束条件：实际输出空间电压矢量us的α轴分量usα和β轴分量usβ的基波幅值保持相等。下面给出证明：

先证必要性，假设输出三相电压的基波幅值相等为U，则三相电压可表示为：

由式（10）可知，若三相相电压基波幅值相等，则空间电压矢量us的α轴分量usα和β轴分量usβ的基波幅值也相等。

再证充分性，假设空间电压矢量us的α轴分量usα和β轴分量usβ的基波幅值相等为U，且满足：

因此，根据上述约束条件可知，现有过调制策略在将输出电压展开成傅里叶级数时，只考虑了us的α轴分量usα基波幅值等于ua的基波幅值，忽视了对β轴分量usβ的约束，导致实际输出电压的三相不平衡[5]。针对此问题，在设计过调制算法时，充分考虑上述约束条件，提出了一种能够输出三相平衡电压的过调制策略。

2.2 过调制I区（m1

由于参考电压矢量Ur超出四边形区域的部分不能实际输出，因此，需对参考电压矢量Ur进行调整，调整后的参考电压矢量称为补偿电压矢量，用U*r表示。

定义过调制系数为

当k1=0时，线性调制区结束，过调制I区开始，即实际输出电压矢量轨迹为四边形内切圆;当k1=1时，过调制I区结束。

在过调制I区，参考电压矢量的调整过程如图4所示。

由图4可知，参考电压矢量Ur在第一扇区的调整过程可分為以下两部分。

1）参考电压矢量Ur相位满足0≤θ<π/3。

四边形内切圆对应的电压矢量表达式为

位于四边形边沿上的电压矢量为

该区域的补偿电压矢量U*r位于四边形内切圆电压矢量urins和四边形边沿电压矢量urq之间，即一方面将超出四边形边界的电压矢量维持于四边形边界，另一方面增大未超出四边形边界部分的电压矢量幅值以保证实际输出电压基波幅值等于参考电压基波幅值。如图4所示，根据叠加定理，此时的U*r可由加权系数为（1-k1）的urins和加权系数为k1的urq合成，即

2）参考电压矢量Ur相位满足π/3≤θ<π/2。

如图4所示，以OD为半径的圆弧为逆变器运行于过调制Ⅰ区上限时，实际输出电压矢量的轨迹，对应的圆矢量可表示为

式中a为待定常数。

该区域的补偿电压矢量U*r位于四边形内切圆电压矢量urins和圆弧电压矢量urm之间，如图4所示，根据叠加定理，此时的U*r可由加权系数为（1-k1）的urins和加权系数为k1的urm合成，即

将Uα和Uβ展开成傅里叶级数形式，则其基波幅值可表示为：

由上文分析可知，为输出平衡的三相电压，必须满足约束条件：实际输出空间电压矢量的α轴分量和β轴分量的基波幅值相等，即

下面求待定系数a，以及过调制I区与过调制Ⅱ区的临界调制比m2。

由于逆变器运行于过调制Ⅰ区上限时，圆弧电压矢量urm为部分实际输出电压矢量，故将k1=1代入式（16）、式（18），并联立式（14）～式（21），可求得a=0.943 9。将a值代入到此时的UαFm表达式中，并联立式（8），可求得m2=0.948 9。

将求得的m2值和a值分别代入式（13）、式（17），联立式（13）～式（21），得到过调制Ⅰ区Uα、Uβ的基波幅值与调制比m的关系为

2.3 过调制II区（m2

首先定义过调制系数为

当k2=0时，过调制Ⅰ区结束，过调制Ⅲ區开始;当k2=1时，过调制Ⅱ区结束。

在过调制Ⅱ区，参考电压矢量的调整过程如图5所示。

在过调制Ⅲ区，参考电压矢量的调整过程如图6所示。

下面求过调制Ⅲ区上限处的最大调制比mmax。

由于逆变器运行于过调Ⅲ区上限时，实际输出电压矢量轨迹已知，故将k3=1代入式（31），并联立式（8）、式（21）、式（24）和式（30）～式（31），可求得mmax=1.154 7。

将求得的mmax值代入式（29），联立式（15）、式（19）、式（20）、式（24）和式（29）～式（31），得到过调制Ⅲ区Uα、Uβ的基波幅值与调制比m的关系为

3 仿真研究与实验验证

3.1 仿真研究

为了验证理论分析的正确性，在MATLAB/Simulink环境下搭建了系统的仿真模型，对所提出的考虑输出电压平衡的三相四开关逆变器SVPWM过调制策略与传统的过调制策略进行了仿真对比研究。模型中，采用和被试实验电机相同的参数，如表2所示，直流侧电压取480 V，开关频率取1.2 kHz。

定义输出比Q为输出相电压基波幅值与直流母线电压值之比，图7为过调制区域输出比Q与调制比m的关系，可以看出，两者呈线性关系。

逆变器运行频率为50 Hz，1.04 s时刻调制算法从传统过调制算法切换到所提出的基于叠加定理的过调制算法，图8为过调制区域调制比m分别为0.93、0.96、1和1.13时，对逆变器输出的相电压PWM波形进行低通滤波后的波形，以及相电压PWM波形的基波幅值（利用Matlab软件的“Fourier模块”实现PWM波形的基波幅值提取）。

由图8可以看出，对于整个过调制区域，在所提基于叠加定理的过调制策略作用下，实现了三相基波电压的平衡输出，同时在过调制I区与过调制II区，逆变器输出的三相相电压波形质量明显优于传统的过调制方法。对于过调制III区，其一般仅短时应用于对直流电压利用率有最高要求的特定工况，由于此时PWM脉冲数目较少，两种调制策略下输出电压的低次谐波所占比重均较大，即便如此，相对于传统方法，所提方法此时仍可实现三相基波电压的平衡输出。

3.2 实验验证

在理论分析和仿真研究基础上，搭建了基于TMS320F28335的两电平逆变器实验平台，实验参数与仿真参数一致。

在调制比分别为0.93、0.96、1和1.13的条件下，进行两种过调制策略的对比实验。利用横河示波器DLM2024测得了不同调制比下线电压PWM波形uab和ubc，滤除高次谐波后的线电压波形u～ab和u～bc，以及uab和ubc的FFT分析结果，如图9所示。为使实验对比结果更加直观、确切，一方面，对图9中FFT分析结果进行了局部放大处理（见图中虚线框）;另一方面，通过横河示波记录仪DL850E对逆变器输出线电压进行了数据存储，进一步将所测得的数据导入到Matlab中，利用其FFT分析功能得到线电压基波幅值UFab和UFbc的实验值，如表3所示。

对实验结果进行分析，可发现其与仿真结果基本相符。在过调制I区和过调制II区，所提出的过调制方法输出的线电压波形平衡性与正弦度得到有效改善，随着调制比的增大，改善效果愈发明显。在机车重载运行、矿井重物牵引等需要高输出电压的特殊工况，调制比可进一步增大，进而进入过调制III区，此时输出电压的PWM波形由密变疏，低次谐波逐渐增大。由图9（g）和图9（h）可知，受3次谐波影响，两种过调制方法输出的u～ab和u～bc波形均出现一定畸变，即使输出电压谐波成分较复杂，但此时应用所提方法得到的uab和ubc基波幅值仍然相等。由图9中的FFT频谱分析和表3可以发现，所提出的基于叠加定理的过调制策略，可实现整个过调制区域三相基波电压的平衡输出。同时，由表3可知，新提出的过调制策略很好地解决了传统过调制策略线电压实际输出值与理论值存在较大偏差的问题，可使实际输出值维持在理论值附近，偏差限制在3 V以内。

4 结 论

本文以三相四开关逆变器为研究对象，通过对传统过调制策略进行分析，指出了逆变器输出三相电压不平衡的原因，针对该问题，提出了基于叠加定理的SVPWM过调制策略。通过与传统过调制策略进行仿真和实验对比，验证了所提过调制策略的正确性和可行性，并得出以下结论：

1） 三相四开关逆变器输出平衡三相电压的约束条件：实际输出空间电压矢量的α轴分量和β轴分量的基波幅值相等;

2） 所提过调制策略避免了传统方法复杂的三角函数实时计算和预先存储数据，减轻了计算负担，易于数字化实现;

3） 实现了在整个过调制区域三相电压的平衡输出，并且进一步提高了直流电压利用率。

参 考 文 献：

[1] 孙丹， 何宗元， BLANCO I Y， 等. 四开关逆变器供电永磁同步電机直接转矩控制系统转矩脉动抑制[J].中国电机工程学报， 2007， 27（21）： 47.

SUN Dan， HE Zongyuan， BLANCO I Y， et al. Torque ripple reduction for a fourswitch inverter fed PMSM DTC system[J]. Proceedings of the CSEE， 2007， 27（21）： 47.

[2] 滕青芳， 李国飞， 朱建国， 等. 三相四开关容错逆变器的PMSM驱动系统FCSMPC策略[J].电机与控制学报， 2016， 20（10）： 15.TENG Qingfang， LI Guofei， ZHU Jianguo， et al. Finitecontrolset model predictive control for PMSM systems driven by threephase fourswitch faulttolerant inverter[J]. Electric Machines and Control， 2016， 20（10）： 15.

[3] BADSI B El， BOUZIDI B， MASMOUDI A. DTC scheme for a fourswitch inverter fed induction motor emulating the sixswitch inverter operation[J]. IEEE Transaction on Power Electronics， 2013， 28（7）： 3528.

[4] 王文， 罗安， 黎燕. 三相四开关并联有源电力滤波器的控制方法[J]. 电工技术学报， 2014， 29（10）： 183.WANG Wen， LUO An， LI Yan. Control method of threephase fourswitch shunt active power filter[J]. Transactions of China Electrotechnical Society， 2014， 29（10）： 183.

[5] 安群涛， 孙醒涛， 赵克， 等. 容错三相四开关逆变器控制策略[J]. 中国电机工程学报， 2010， 33（3）： 14.AN Quntao， SUN Xingtao， ZHAO Ke， et al. Control strategy for faulttolerant threephase fourswitch inverters[J]. Proceedings of the CSEE， 2010， 33（3）： 14.

[6] 黄凯， 郭源博， 戴碧君， 等. 容错型牵引电机驱动系统的间接定子量控制[J]. 哈尔滨工业大学学报， 2016， 48（9）： 157.HUANG Kai， GUO Yuanbo， DAI Bijun， et al. Indirect statorquantities control of faulttolerant traction drive system[J]. Journal of Harbin Institute of Technology， 2016， 48（9）： 157.

[7] WANG R， ZHAO J，LIU Y. A comprehensive investigation of four switch threephase voltage source inverter based on double Fourier integral analysis[J]. IEEE Transaction on Power Electronics， 2011， 26（10）： 2774.

[8] CORRA M B R， JACOBINA C B， DA SILVA E R C， et al. A general PWM strategy for fourswitch threephase inverter[J]. IEEE Transactions on Power Electronics， 2006， 21（6）： 1618.

[9] DZUNG P Q， PHUONG L M， VINH P Q，et al. New space vector control approach for four switch three phase inverter （FSTPI） [C]// International Conference on Power Electronics and Drive Systems，November 27-30，2007，Bangkok，Thailand.2007：1002-1008.

[10] ZENG Z Y， ZHU C， JIN X L， et al. Hybrid space vector modulation strategy for torque ripple minimization in threephase fourswitch inverterfed PMSM drives[J]. IEEE Transactions on Power Electronics， 2017， 64（3）： 2122.

[11] NGUYEN T D， NGUYEN H M， LEE H H. Adaptive carrierbased PWM for a fourswitch threephase inverter under DClink voltage ripple conditions[J]. Journal of Electrical Engineering and Technology， 2010， 5（2）： 290.

[12] 吳德会， 夏晓昊， 张忠远， 等. 基于三相桥臂坐标的SVPWM过调制方法[J]. 电工技术学报， 2015， 30（1）： 150.WU Dehui， XIA Xiaohao， ZHANG Zhongyuan， et al. A SVPWM overmodulation method based on threephase bridge arm coordinates[J]. Transactions of China Electrotechnical Society， 2015， 30（1）： 150.

[13] 吴晓新， 柳巍， 阮毅， 等. 一种SVPWM过调制算法及其在两电平逆变器中的应用[J].电机与控制学报， 2015， 19（1）：76.WU Xiaoxin， LIU Wei， RUAN Yi， et al. SVPWM overmodulation algorithm and its application in twolevel inverter [J]. Electric Machines and Control， 2015， 19（1）：76.

[14] 樊扬， 瞿文龙， 陆海峰， 等. 基于叠加原理的SVPWM过调制算法[J]. 清华大学学报（自然科学版），2008， 48（4）： 461.FAN Yang， QU Wenlong， LU Haifeng， et al. SVPWM overmodulation algorithm based on superposition principle[J]. Journal of Tsinghua University（Science and Technology），2008， 48（4）： 461.

[15] SUN K， WEI Q， HUANG L P， et al. An overmodulation method for PWMinverterfed IPMSM drive with single current sensor[J]. IEEE Transactions on Industrial Electronics， 2010， 57（10）： 3395.

[16] 刘贺， 姜建国， 乔树通. 一种应用于多电平SVPWM的过调制算法[J]. 电机与控制学报， 2016， 20（1）： 7.LIU He， JIANG Jianguo， QIAO Shutong. An overmodulation scheme of SVPWM used in multilevel inverters[J]. Electric Machines and Control， 2016， 20（1）： 7.

（编辑：邱赫男）