逐步判别分析方法在新北油田水淹层识别中的应用

马福军，李 楠，刘 刚，王 婷

(中国石油吉林油田分公司，吉林 松原 138000)

新北油田区域构造位于松辽盆地中央坳陷区扶余华字井阶地的扶余-新立背斜构造北翼，是一个高渗透、被断层复杂化的构造岩性油藏，1978年以425 m反九点法面积注水方式全面投入开发，开发目的层为黑帝庙油层。1994年加密调整成300 m反九点法面积注水井网，2001年再次加密调整成212 m反九点法面积注水井网，现已进入高含水期开发阶段。随着油田水驱开发程度的不断提高，油田的水淹程度日趋增高，导致油层的流体性质、孔隙结构、岩石的物理化学性质以及油气水分布规律等都会发生一定程度的变化[1-7]，使得调整井水淹层解释相对复杂化，解释结果与实际符合率相对较低。尤其在近几年，老区调整新井投产后的实际水淹情况与测井解释结果相差较大，统计2015年完钻投产井实际含水与测井解释符合程度为75.4%，严重影响了产能形象。水淹层识别研究是油田开发后期开发调整的关键，近几年测井技术人员也相应开展了水淹层机理方面的研究，但仍没有突破性进展，因此，我们在分析油层水淹对测井响应产生的主要变化基础上，采用逐步判别分析方法来识别水淹层，提高水淹层识别与实际的符合程度,为油田开发后期调整井水淹层的识别提供新的思路和方法。

1 逐步判别分析的基本原理

判别分析是判别样品所属类型的一种统计方法[8-12]，其主要思想就是用统计方法将待判样品与已知样品进行类比，确定待判样品归属于那一类。实际往往常用的是多组线性判别方法，考虑尽可能多的变量来区分总体，但每个变量所携带的地质信息不同，对区分总体判别的贡献不一样，为此采用逐步判别方法，变量有进有出，每一步都对变量贡献进行检验，在把一个重要变量引入判别函数后，同时考虑到较早引入判别函数的某些变量随着新变量的引入而变得不重要，将其从判别函数中剔除,最终保留有“重要性”的变量，使判别函数更加简洁实用。 其计算步骤如下：

设有m个总体，第g总体有ng个样品，每个样品均观测了p项指标，原始数据记为：

Xgjk(g=1,2……,m;j=1,2,……,ng;k=1,2……,p)

(1)

式中：Xgjk表示第g组第j个样品的第k项指标。

首先计算出各组变量均值Xgk和总均值Xk，组内离差矩阵W与总离差矩阵T。

1.1逐步筛选变量

用Wilks统计量U来检验p个变量区分m个总体的能力。U是矩阵W与矩阵T行列式值之比。

1.1.1引入变量

按式(2)对未引入的变量Xi计算判别能力Ui,选出判别能力最大的变量Xr，并按式(3)计算出F1，若F1>Fa(m-1,N-m-l),则Xr引入判别式。

Ui=Wii/Tii

(2)

式中：Ui是第i个变量的判别能力；Wii是组内离差矩阵i行i列元素；Tii总离差矩阵i行i列元素。

(3)

式中：F1是引入变量的F检验值；l是判别式已引入的变量数，N是m个总体全部样品总数(N=n1+n2…+ng)。

1.1.2剔除变量

按式(4)对已引入的变量Xj计算判别能力Uj,选出判别能力最小的变量Xr,并按式(5)计算出F2，若F2≤Fa(m-1,N-m-l+1)，则Xr判别力不显著，从式中剔除。

Uj=Tjj/Wjj

(4)

式中：Uj是第j个变量的判别能力；Wjj组内离差矩阵j行j列元素；Tjj总离差矩阵j行j列元素。

(5)

式中：F2是剔除变量的F检验值。

每引入或剔除一个变量都要对矩阵W与T进行一次求解求逆并行变换[7]，重复式(2)～(5)计算步骤，直到没有变量可以剔除，也没有变量可以引入为止，筛选变量完成。

1.2计算判别函数

筛选变量结束后，方程最终已引入了D个变量，可算得各组判别函数如下：

(6)

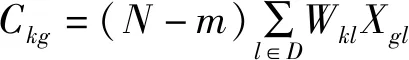
式中，Ckg为判别函数的系数；Cog为判别式中常数项；D为方程最终引入的变量个数。

1.3分组判别

设一样品为X=(x1,x2，……，xp)，将它代入式(6)算出m个判别函数值。

2 判别分析方法在水淹层识别中的应用

油层水淹级别划分是按含水百分数大小划分，按标准分为5个级别，见表1。

表1 油层水淹级别划分标准

地质工程师通过多年来对水淹层识别方法的研究[13-16]，认为油层水淹后在测井响应引起变化的主要指标有：0.5 m电阻率、声波时差、自然伽马、孔隙度、渗透率和含油饱和度。

为此，我们选择这6项测井参数作为逐步判别的指标变量，建立判别函数。

2.1 逐步判别分析判别函数的建立

收集新北油田2015年完钻投产的30口井生产数据。

由于注水开发时间较长，老区不存在未水淹层，因此只建立弱水淹层、中水淹层、强水淹层和特强水淹层4个级别的判别函数，其数据见表2。

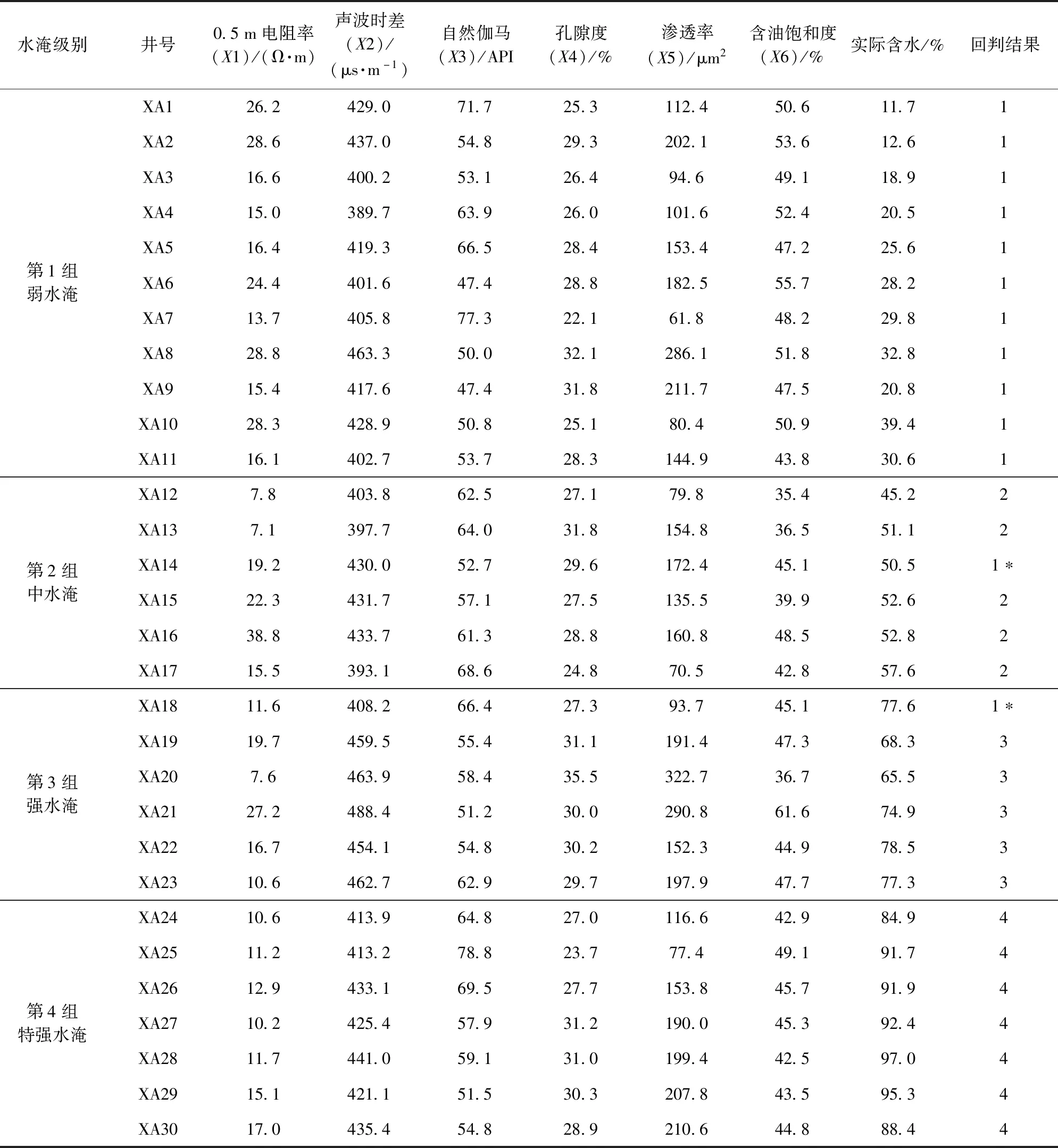
表2 新北油田30口井各项指标与水淹级别数据

注：回判结果：1.弱水淹；2.中水淹；3.强水淹；4.特强水淹；*.与实际不符。

用表2中X1～X6的6列数据，按式(1)构成4个总体6个指标数据，经式(2)～(6)计算，最终有3个变量引入判别函数，分别是0.5 m电阻率、声波时差和含油饱和度。其4个总体的判别函数如下：

第1组:F1(x)=-443.694 5-4.957 8x1+1.778 1x2+4.913 6x6

第2组:F2(x)=-411.204 8-4.657 3x1+1.758x2+4.243 5x6

第3组:F3(x)=-529.860 5-5.468 2x1+1.980 8x2+5.043 1x6

第4组:F4(x)=-475.674 9-5.248 5x1+1.869 9x2+4.864x6

式中：x1是0.5 m电阻率，Ω·m；x2是声波时差，μs/m；x6是含油饱和度，%。

2.2 逐步判别分析判别函数的显著性检验

逐步判别分析建立的判别函数使各总体间差异最大，总体内差异最小，所建的判别模型需验证显著性，通常有两种方法：一是回判率检验，二是总体间显著性检验。

2.2.1 回判率检验

为了验证所建判别函数的显著性，将原始样品代入所建判别函数中进行回判，一般认为，回判正确率大于75%，判别函数有效[8，17]。经原始样品数据代回判别式，其回判结果见表2，中水淹层判错1口，强水淹层判错1口，弱水淹层和特强水淹层全部判对，总体看30口井判对28口井，回判正确率为93.3%，所建立的判别函数可应用于实际水淹层识别。

2.2.2 总体间显著性检验

把总体两两配对逐次检验两总体间的显著性，用马氏距离构成的统计量[12，17]Fef来检验，通过计算两两总体间马氏距离和统计量Fef检验值(见表3)，总体内两类间的Fef值均大于Fa(a=0.1)的值。检验效果显著，判别函数可有效区分两两总体，所建模型可靠。

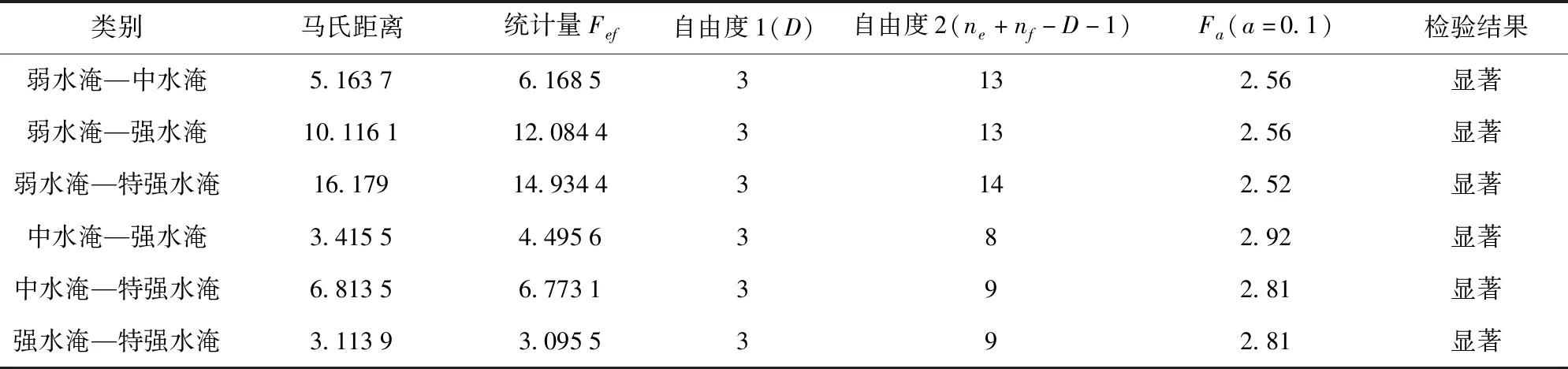
表3 4个总体两两分类间判别效果检验

2.3 判别函数的实际应用

2.3.1 应用实例

应用所建立的判别函数对2018年完钻的12口井进行水淹层识别，结果见表4，与试油生产实际数据对比，其中1口井XB10实际是中水淹，判别函数识别成弱水淹了，其余11口判别函数识别结果与实际相符，说明所建的判别函数符合实际。

2.3.2 逐步判别方法与测井解释方法效果对比

从这12口井测井解释结果与实际对比看，其中4口井与实际含水不相符，测井解释结果符合率为66.7%,逐步判别方法符合率为91.7%，远高于测井解释的符合率。图1是XB9井新旧方法解释成果对比，测井解释结果是中水淹，试油结果是强水淹，逐步判别结果是强水淹，可以看出逐步判别方法识别水淹层与测井解释结果对比具有较高的识别精度。

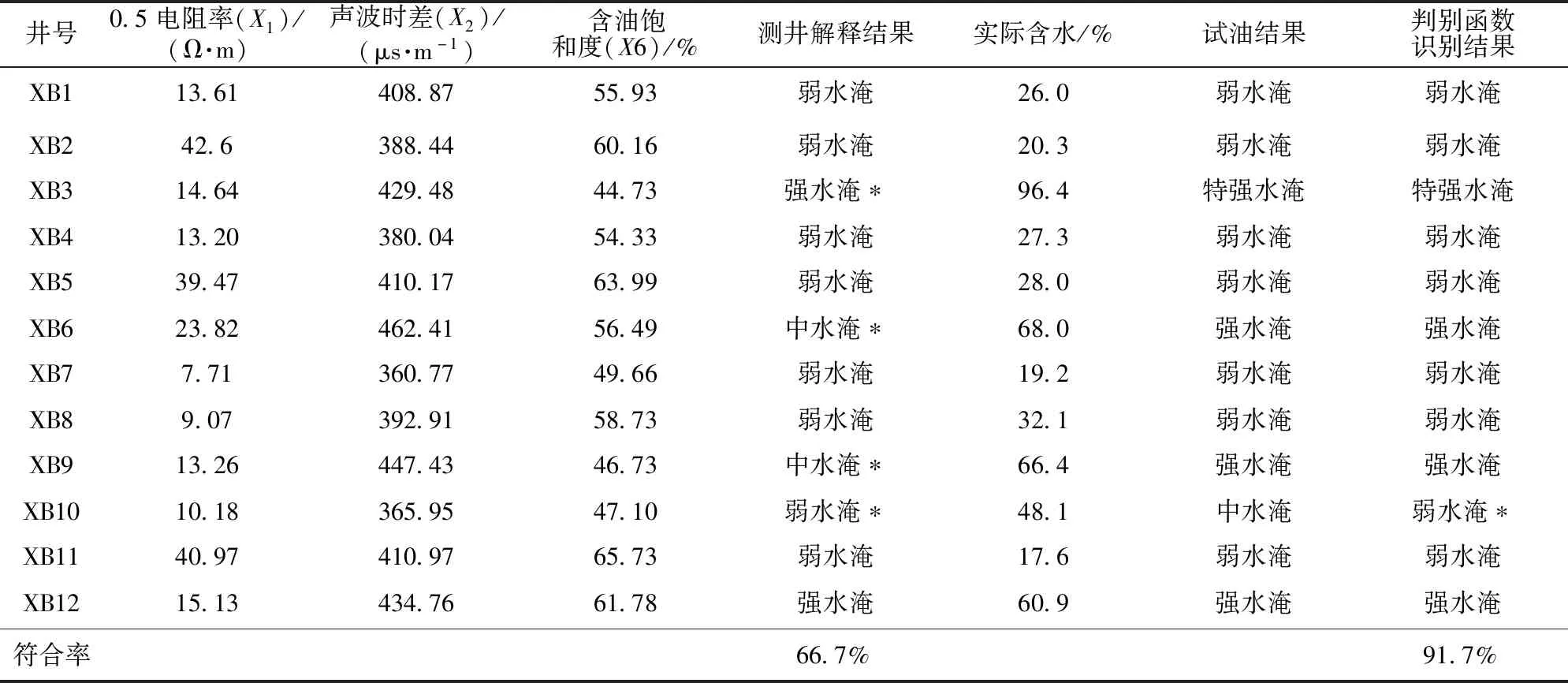
表4 新北油田2018年12口调整井水淹级别识别情况

注：*与实际不符。

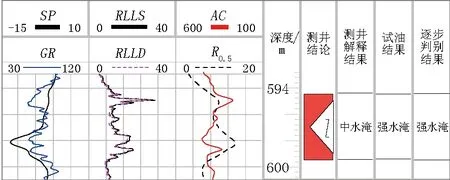
图1 XB9井测井解释与判别分析成果对比

2.4 误差分析

分析造成误差的原因主要有两个方面：一是影响油层水淹的因素较多，每个因素所携带的信息量和对函数的贡献不同[18]，逐步判别分析过程忽略了某些因素的影响，导致产生一定的误差；二是用于建立判别函数的原始观测数据的离散程度也是产生一定误差的一个原因，原始数据有规律性且代表性强，所建立的判别函数精度就高，误差就小，若原始数据比较离乱，所建立的判别函数精度就差，误差就会偏大。从所选的原始数据建立判别函数和实际应用对比看，达到了较高的识别精度，能较好地满足实际需要。

3 结论

(1)采用了逐步判别分析方法识别水淹层，从相关测井指标中优选出与油层水淹相关的指标来建立逐步判别函数，能有效识别水淹层级别，经实际检验，达到了较好的识别精度，为新北油田开发后期调整井水淹层识别提出了新的思路和方法。

(2)逐步判别分析方法已被多个领域广泛应用，对于建立的判别函数的精度和实用性，取决于所选建立函数样本数据的数量和代表性，已知样品数量越多代表性越强时，所得的判别函数就越可靠，所以优选原始数据很重要。

(3)用新北油田数据建立的判别函数最适用于新北地区的油层水淹识别，而且效果非常好，但不一定适合其他地区的水淹层识别，针对不同地质特征油田用自己油田的数据建立不同的判别函数，才能有更好的识别效果。