含齿根早期裂纹损伤的行星齿轮箱故障机理研究

张 俊，李习科，汪 建，姚立纲，刘先增

含齿根早期裂纹损伤的行星齿轮箱故障机理研究

张 俊1，李习科1，汪 建1，姚立纲1，刘先增2

(1. 福州大学机械工程及自动化学院，福州350116；2. 天津大学机械工程学院，天津 300350)

行星齿轮箱中齿根早期裂纹损伤的故障特征微弱，导致其难以被识别．为揭示齿根早期裂纹的故障机理，采用集中参数法建立计入裂纹损伤效应的行星齿轮箱传动-结构耦合非线性动力学模型．首先，基于势能法建立含齿根裂纹损伤的齿轮副啮合刚度与传动误差计算模型，通过刚度激励函数与位移激励函数将裂纹损伤的效应纳入行星传动系统的非线性动力学模型，进而求解行星传动系统的振动响应，结果表明内、外传动支路之间的传动误差差异导致各支路载荷分配不均．其次，采用ANSYS Workbench建立箱体结构的有限元模型．将行星传动系统中太阳轮、行星架以及内齿圈的支承反力施加于箱体结构的相应轴承座处，并通过窗函数计入行星架旋转对信号的调制效应以获取行星齿轮箱的振动信号；通过对箱体振动信号的频谱分析，提取了行星齿轮箱齿根早期裂纹损伤的故障特征．最后，搭建动力传动故障模拟实验台，对存在齿根早期裂纹损伤的行星齿轮箱进行了振动测试．仿真信号与实测信号基本一致，表明所建行星齿轮箱传动-结构耦合动力学模型能准确揭示行星齿轮箱齿根早期裂纹损伤的故障机理．行星齿轮箱中齿根早期裂纹损伤的故障特征表现为以啮合频率为中心、故障特征频率的分数倍频及行星架转频为间隔的调制边带．

行星齿轮箱；齿根早期裂纹；故障特征；调制边带

齿根早期裂纹是行星齿轮箱中难以识别且危险程度较高的损伤模式之一．造成其难以被识别的主要原因有：①齿根早期裂纹引起的冲击信号微弱，使其容易被传动系统原有的振动信号所淹没；②微弱故障信号在经传动支路(齿轮—轴—轴承)传递到探测点的过程中逐渐被削弱．虽然故障特征微弱导致齿根裂纹难以被识别，但其高危险性又迫切要求识别出这一故障模式．为保障行星齿轮箱的安全运行，必须探明齿根早期裂纹的故障机理，建立故障与征兆间的内在联系与映射关系，这是诊断行星齿轮箱齿根早期裂纹损伤的理论基础．

围绕齿根裂纹的故障机理，学术界开展了大量研究[1-2]．齿根裂纹影响传动系统的内部激励，进而改变行星齿轮箱的振动特性．Wan等[3]计算了含裂纹损伤齿轮副的啮合刚度，并分析了裂纹损伤对齿轮-转子系统振动特性的影响．马锐等[4]分析了裂纹演化对齿轮副啮合刚度及单自由度齿轮系统动力学行为的影响．这些研究反映了含齿根裂纹传动系统的振动特性，但其中未考虑箱体结构的影响．

箱体作为传动支路的支承构件，其结构对振动特性具有显著影响，而结构的复杂性使其难以直接处理为集中参数模型．研究结果[5-8]表明：采用有限单元法可以提取箱体结构在连接节点处的集中参数，将提取的箱体质量、刚度、阻尼等参数引入传动系统模型，以此获得箱体结构对行星传动系统振动特性的影响．然而，箱体结构上任一探测点振动特征是有所区别的，因此集中参数法对分析不同探测点的振动特性并不适用．更为重要的是，这一方法未考虑箱体结构对振动传递特性的影响．

关于振动传递特性的研究，雷亚国等[9-10]建立了含“双抛物线”型齿根裂纹及“矩形状”剥落的齿轮副损伤模型，将其纳入传动系统动力学模型，构建了行星齿轮箱振动信号仿真模型，并据此分析了2种故障模式的振动响应特性，但所建的传动系统动力学模型仅考虑了各构件的扭转变形及太阳轮的平移变形．Liang等[11-12]进一步完善这一模型，建立了行星系统平移-扭转耦合动力学模型，通过加窗函数的方法模拟了行星架旋转对探测点信号的调制效应，并开展了齿根裂纹损伤的故障诊断．而这一研究所获取的行星齿轮箱振动信号是根据行星轮沿垂直方向的振动加速度合成的．Inlpolat等[13]与Liu等[14]则分别以内、外齿轮副啮合力和啮合线上的振动加速度为基础建立行星齿轮箱的振动信号模型．虽然上述研究考虑了传递路径的影响并建立振动信号模型，但啮合力和啮合线上的振动加速度均未考虑箱体结构、材料属性和探测点位置等对合成振动信号的影响，进而未能准确建立合成振动信号与力或加速度之间的映射关系．

针对以上问题，本文建立了传动-结构耦合动力学模型，并采用龙格-库塔法求解行星传动系统的无量纲动力学方程，将解得的动态响应作为箱体结构的激励．传动系统建模表征了齿根早期裂纹损伤的演化机理，箱体结构有限元建模则模拟了振动信号在箱体结构中的传递特性．搭建了动力传动故障模拟实验台，通过仿真与实验的对比，验证了所建传动-结构耦合动力学模型及参数计算方法的准确性．综合以上分析，揭示了齿根早期裂纹的故障机理，希冀为行星齿轮箱齿根早期裂纹的故障诊断提供理论依据．

1 传动系统动力学建模

1.1 齿根裂纹损伤建模

以30°切线法(＝30°)确定裂纹起始临界点的位置，建立齿根裂纹损伤模型，如图1所示．图1中：为裂纹扩展角；为裂纹深度；m为啮合轮齿之间的法向载荷；a、b为法向载荷的径向分力和切向分力；12为轮齿中线；为啮合点到基圆的距离；h为齿廓上任一点到中线的距离；为这一点到基圆的距离；c1为裂纹损伤轮齿齿廓受力边界线上任一点到中线的距离；为啮合点到中线的距离；为齿廓上距离基圆位置处对应的齿轮转角；1为齿廓上啮合点对应的齿轮转角；g为齿廓上裂纹终点位置对应的齿轮转角；b、f分别为基圆半径和齿根圆半径；b、f分别为基圆和齿根圆对应的中心角的一半；段为齿顶圆齿廓；段为渐开线齿廓；段为过渡圆弧齿廓；r为过渡圆弧半径；f为法向载荷线与中线交点到齿根圆的距离；f为齿根圆齿厚．

图1 齿根裂纹示意

基于渐开线齿轮的啮合原理，采用势能法计算太阳轮-行星轮及行星轮-内齿圈的啮合刚度．因轮齿挠曲变形储存在啮合轮齿中的势能可表示[3]为

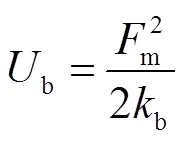
式中：b为弯曲势能；s为剪切势能；a为压缩势能；b为弯曲刚度；s为剪切刚度；a为压缩刚度．

各项势能计算式分别为

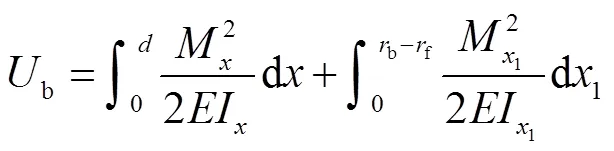
啮合刚度需计入接触刚度h及基体刚度f，即

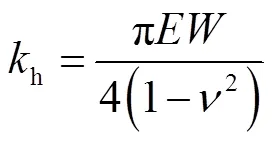
(6)

式中：为轮齿齿宽；为泊松比．篇幅所限，其他参数的定义及取值详见文献[15]．

一般地，直齿齿轮副的重合度介于区间(1，2). 由式(1)～(6)计算单齿啮合区的啮合刚度，即

而在双齿啮合区，两对啮合轮齿共有1个轮体，引入基体刚度修正系数减小啮合刚度偏差，得到双齿啮合刚度为

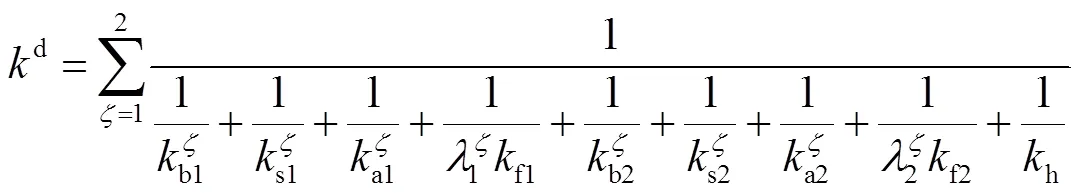
为便于数值求解，将内、外齿轮副的啮合刚度曲线拟合成傅里叶级数形式，即

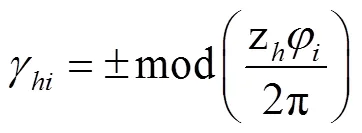
＝s，r；＝1，2，…，

由误差分析[18]可得齿轮副的传动误差E为

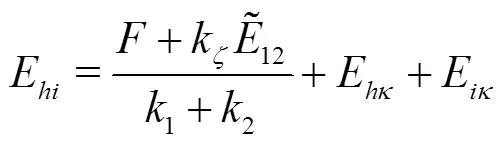
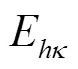
同样地，将内、外齿轮副的传动误差曲线拟合成傅里叶级数形式，即

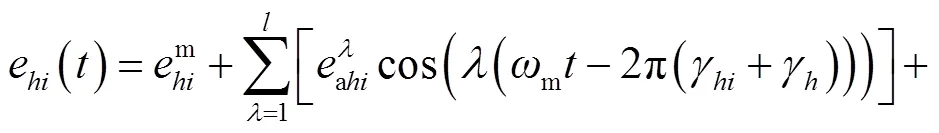
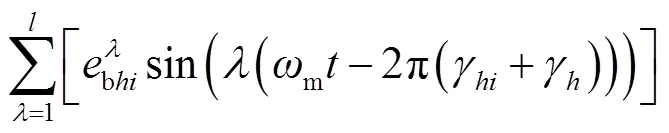
1.2 传动系统动力学模型

不失一般性，以2K-H型直齿行星轮系为对象，建立传动系统的非线性动力学模型，如图2所示．该行星轮系由太阳轮s、行星架c、内齿圈r和个均布的行星轮p等构件组成．其中，太阳轮s为输入构件，行星架c为输出构件，内齿圈r与箱体结构固联．为清晰起见，仅绘出了行星轮1．

为方便建模推导，做如下处理：①将各齿轮简化为具有集中质量的圆柱体，忽略轮体结构柔性；②各内、外齿轮副以弹簧阻尼单元表示，弹簧的弹性系数和阻尼器的阻尼系数为啮合刚度和啮合阻尼；③忽略啮合轮齿的摩擦效应，且各构件振动只发生在垂直于其轴线的平面内；④在轮系几何中心处建立随行星架同步旋转的中心构件连体坐标系，其轴通过行星轮p1的几何中心1，轴与轴垂直，且相位超前90°；在各行星轮几何中心O建立行星轮连体坐标系Oxy，其中x轴由点指向O点，y轴与x轴垂直，且相位超前90°．

图2 行星轮系的非线性动力学模型

图2中：x、y和u分别为构件(＝c，s，r，)沿、向的平动位移和沿向(绕其轴线方向)的扭转位移；k、k分别为构件在连体坐标系下沿、向和向的轴承支承刚度；c、c分别为构件在连体坐标系下沿、向和向的轴承支承阻尼；si、ri分别为太阳轮、内齿圈与行星轮p的啮合刚度；si、ri分别为太阳轮、内齿圈与行星轮p的传动误差；si、ri分别为太阳轮、内齿圈与行星轮p的啮合阻尼；si、ri分别为太阳轮、内齿圈与行星轮p的啮合间隙；s、c分别为太阳轮、行星架上的输入扭矩和负载扭矩．

1.3 变形协调方程与齿侧间隙函数

如图2所示，构件之间的相对位移关系如下．

(1) 太阳轮-行星轮沿啮合线相对位移为

(2) 行星轮-内齿圈沿啮合线相对位移为

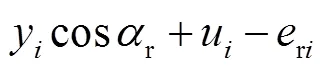
(3) 行星架-行星轮沿、向的相对位移分别为

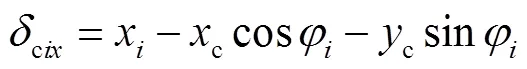
式中：si＝φ－s，为太阳轮与第个行星轮的啮合角，s为太阳轮压力角；ri＝φ＋r，为内齿圈与第个行星轮的啮合角；r为内齿圈压力角．

齿轮啮合时，为形成润滑油膜而不致齿轮“卡死”，内、外啮合齿面之间往往需预留一定的间隙量b．考虑相对位移的齿侧间隙函数表示为

1.4 动力学运动微分方程

以平移位移x、y和扭转位移u(u＝bjθ，bj为齿轮基圆半径，θ为扭转角位移)构成了单一构件的广义坐标向量，＝[x，y，u]，则行星传动系统的广义位移向量为＝[c，s，r，1，2，…，]T．基于牛顿第二定律，推导各构件的运动微分方程并组装成矩阵形式为

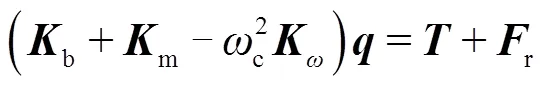
式中：为质量矩阵；为陀螺矩阵；b为支承刚度矩阵；m为啮合刚度矩阵；为向心刚度矩阵；r为内部激励列矢；为外部激励列矢；阻尼矩阵采用Rayleigh阻尼公式表示为

＝＋(b＋m)(19)

式中：为质量比例系数；为刚度比例系数．

由系统无阻尼自由振动，得模态矩阵．通过T和实现刚度矩阵和阻尼矩阵的对角化．

T＝T＋T＝

＋T(20)

式中：为单位矩阵；为模态刚度矩阵；＝b＋m；ξ、ω分别为阶阻尼比和固有频率．取行星传动系统前2阶阻尼比，推导式(21)即可计算质量比例系数及刚度比例系数．

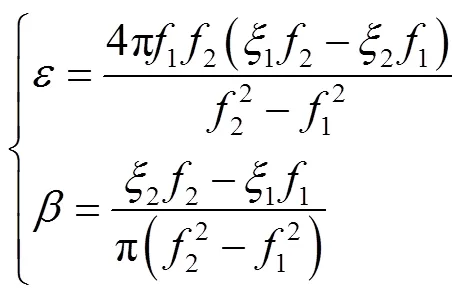
式中：1、2为行星传动系统的前2阶阻尼比；1、2为行星传动系统的前2阶固有频率．

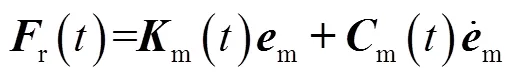
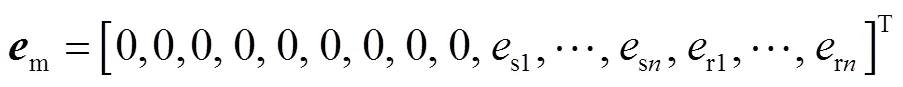
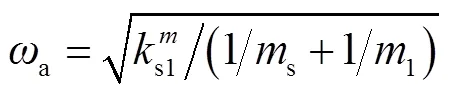
广义位移、速度和加速度等参数转化成无量纲形式，

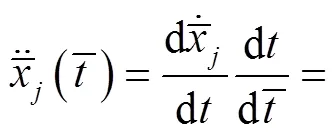
限于篇幅，其他参数的无量纲处理过程不再赘述．将无量纲参数代入式(18)，即可得到行星传动系统的无量纲运动微分方程．行星架、太阳轮、内齿圈和行星轮无量纲运动微分方程分别表示为

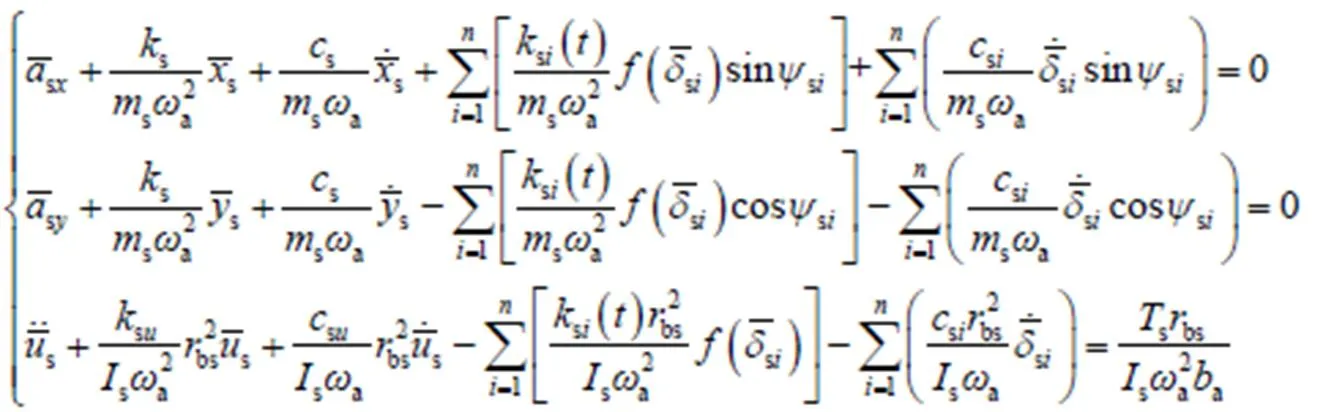
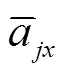
将各构件无量纲运动微分方程转换为无量纲形式

(33)

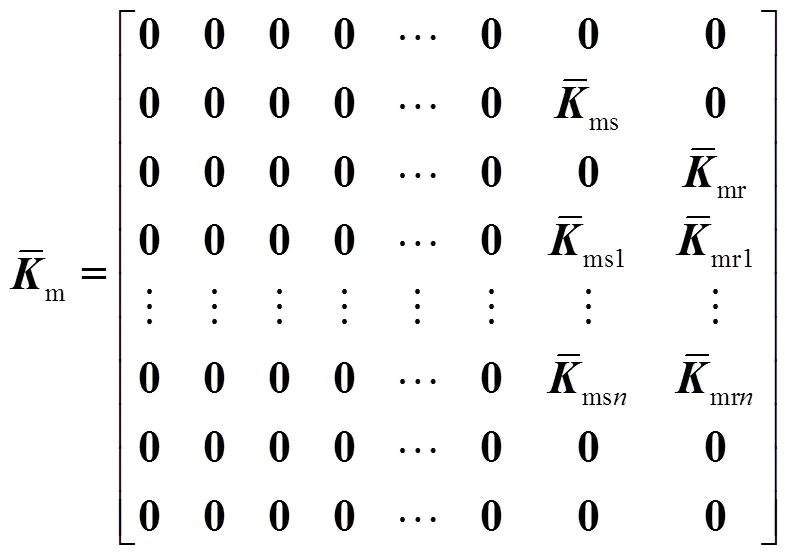
2 动态响应与实验验证

2.1 啮合刚度和传动误差的仿真计算

为方便讨论，以Spectra Quest Inc．公司研发的齿轮动力传动实验台中的行星齿轮箱为案例．齿轮箱中，齿轮精度等级为5级(GB10095—88)；已在太阳轮齿根部位做裂纹损伤预处理，裂纹参数为：扩展角＝70°，深度＝0.5mm，齿根裂纹初始宽度非常小.因此，忽略其初始宽度．计算得到式(19)中的质量比例系数＝160.655，刚度比例系数＝2.487×10-6.构件的其他设计参数与系统工况参数如表1所示．

表1 算例齿轮箱的设计与工况参数

Tab.1 Design and working parameters of example gearbox

行星齿轮箱第1相太阳轮-行星轮(s-p)、行星轮-内齿圈(p-r)的时变啮合刚度如图3所示．傅里叶级数拟合后，啮合刚度谐波系数见表2．

由图3可知，损伤轮齿在啮入至啮出过程，齿轮啮合位置由齿根处移至齿顶处，裂纹降低啮合刚度的幅度逐渐增大．具体而言，当太阳轮齿根部分存在0.5mm深的裂纹时，啮合刚度较健康状态逐渐下降，下降的最大值为6.674N/μm(约为健康轮齿啮合刚度最大值的3.381%)．尽管齿根裂纹降低了齿轮副的啮合刚度，但并不会改变内、外齿轮副的啮合特性，即啮合刚度仍呈现与重合度(外啮合：1.665，内啮合：1.901)变化一致的单—双齿交替啮合规律．

图3 第1相内、外齿轮副的时变啮合刚度

表2 时变啮合刚度谐波系数

Tab.2 Harmonic coefficients of TVMS N/μm

需指出的是不同的扭矩作用下，延长啮合对啮合刚度的影响差异很大．具体表现为扭矩越大，延长啮合的影响越明显[20]．而本文中的系统输入和负载扭矩都很小，故未计入延长啮合的影响．

行星齿轮箱第1相太阳轮-行星轮、行星轮-内齿圈的传动误差如图4所示．傅里叶级数拟合后，传动误差谐波系数见表3．由图4可知，裂纹损伤状态下传动误差与健康状态几乎重合．由此可知，对于齿根裂纹初始宽度小且精度等级较高的齿轮副，齿根裂纹损伤对传动误差的影响是微弱的．

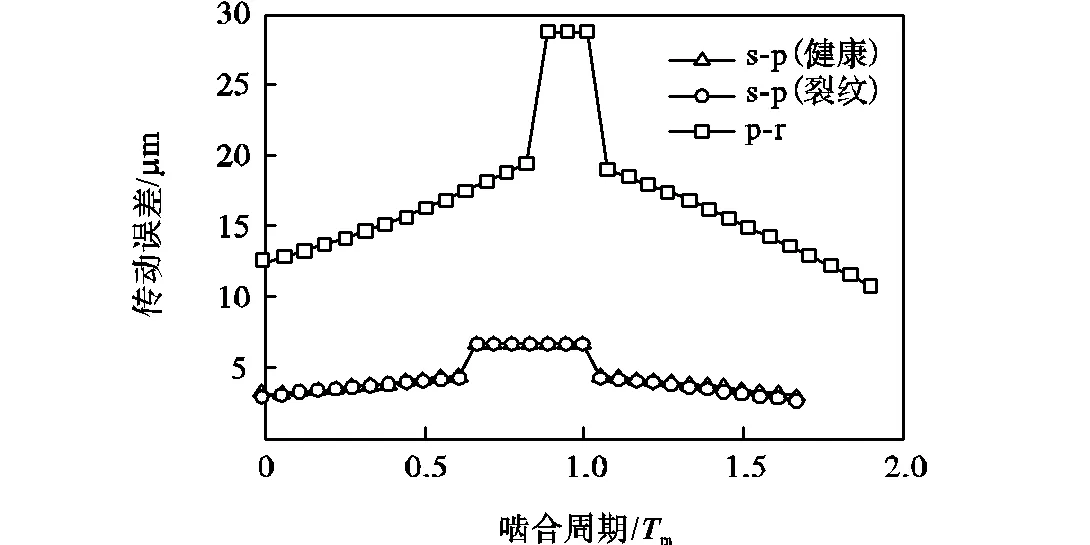
图4 第1相内、外齿轮副的传动误差

表3 传动误差谐波系数

Tab.3 Harmonic coefficients of transmission error mm

2.2 传动系统的动态响应

根据表1中行星齿轮箱的设计和工况参数，采用龙格-库塔法求解方程组(34)，将解得的无量纲动态响应还原为有量纲形式．

图5为健康状态下(内、外传动支路的各项误差一致)，行星轮系中太阳轮沿向的支承力．

由图5可知，太阳轮沿向的轴承支承力呈现出间隔周期为28m的啮合冲击，且每间隔7m出现1次振幅不同的啮合冲击．这一现象可解释如下：该行星齿轮箱中，太阳轮的齿数为28，行星轮个数为4，故存在齿根裂纹的太阳轮相对行星架每旋转一周，裂纹轮齿将分别与4个行星轮上的相应轮齿各啮合1次．换言之，每间隔7m，太阳轮上的裂纹轮齿将与某个行星轮啮合，产生1次啮合冲击；每间隔28m，太阳轮上裂纹轮齿将与同1个行星轮再次啮合，产生1次完全一致的啮合冲击．

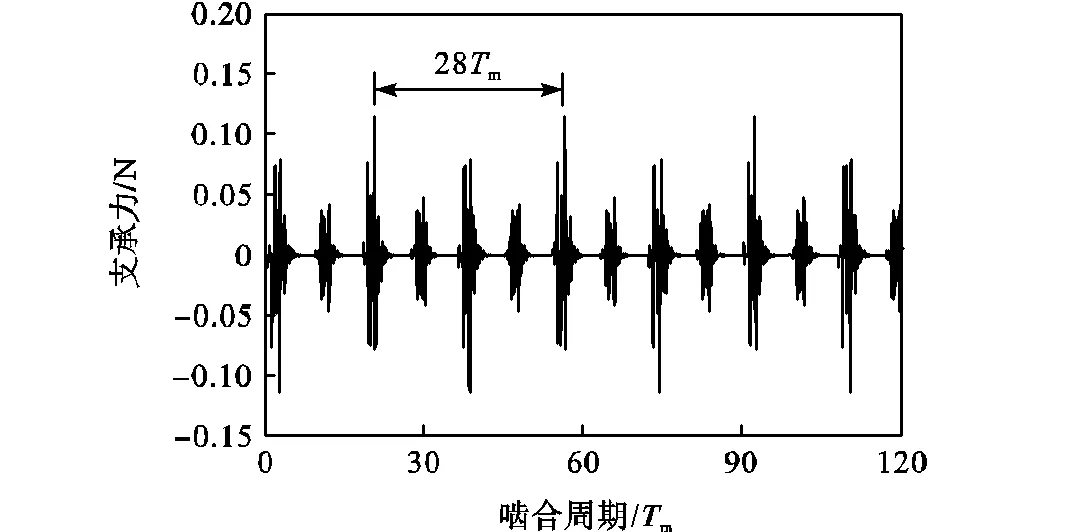
图5 太阳轮沿x向的支承力(健康)

进一步观察可知，由齿根裂纹引起的太阳轮支承轴承力波动幅值很小，冲击力的变化范围为[-0.120，0.120] N，而非啮合冲击处的支承力近似为零．这是由于在不考虑构件制造及安装误差差异的情况下，4条功率流支路完全均载，各相太阳轮-行星轮的啮合力相互抵消，使得轴承支承力近似为零，但就真实工况下的行星齿轮箱而言，其内部必然存在构件制造及安装误差．可以预见，误差会引起功率流支路之间不均载，进而使得轴承支承力的波动幅值远超由齿根裂纹引起的冲击波动．这就容易造成由齿根裂纹损伤引起的微弱振动信号被淹没在位移激励引起的振动信号中．

源于此，不妨考察制造/安装误差导致内、外啮合齿轮副的传动误差间隔相(1、3相和2、4相)分别存在5%、20%的差异时，行星齿轮系统的动态响应．图6为其太阳轮沿向的支承力．

图6 太阳轮沿x向的支承力(裂纹)

由图6可知，计入制造及安装误差后，太阳轮向的振动明显加剧，而在时域响应中，并未呈现由裂纹损伤引起的明显啮合冲击，这一现象与上述预见相符．4条传动支路的位移激励差异导致太阳轮轴承支承力沿局部坐标向发生偏移，轴承支承力的波动范围增大到[-0.215，3.968] N，远高于图5所示的理想状态下的范围[-0.120，0.120] N．由于轴承支承力的波动范围差距悬殊，导致难以识别出时域响应中被淹没的裂纹损伤特征．

尽管如此，采用快速傅里叶变换对轴承力信号进行频谱分析，仍然可以提取到微弱的裂纹故障特征，如图6所示．观察发现，啮合频率m(422.2Hz)两侧呈现出间隔为1/4倍(15.1Hz)裂纹故障频率crack(60.4Hz)的调制边带．这一现象可以解释为：齿轮局部故障的特征频率等价于啮合冲击的重复频率，而在单位时间(1m)内，损伤太阳轮依次与4个行星轮啮合，并产生4次啮合冲击，啮合冲击的重复频率为1/7m(60.4Hz)．再由图5可知，损伤太阳轮与4个行星轮啮合的冲击幅度是不尽相同的，这就导致1次完全一致的啮合冲击的重复频率为1/28m(15.1Hz)，因此，呈现间隔为15.1Hz的调制边带．从边频数量上观察到，仅1/4倍裂纹故障特征频率明显地反映在频谱图中，这一现象说明了裂纹引起的振动冲击所能激起的故障特征频率的阶次数是有限的，从而证明了齿根裂纹损伤引起的振动冲击非常微弱．

根据以上分析足以推断出，图6中所呈现出的边带间隔与行星轮个数是有关的，即行星齿轮箱中的行星轮个数为时，频谱信号中将会表现出以啮合频率为中心、裂纹故障频率的1/分数倍频为间隔的调制边带．

假定内啮合或外啮合齿轮副传动误差间隔相在0～30%范围变化，太阳轮沿向最大支承力见表4.由表4可知，内、外啮合齿轮副的传动误差间隔相在0～30%的范围变化时，太阳轮沿向的最大支承力呈现近似线性递增的变化规律，即太阳轮沿向的最大支承力随着内、外啮合齿轮副传动误差增加而增大.

表4 太阳轮沿向最大的支承力

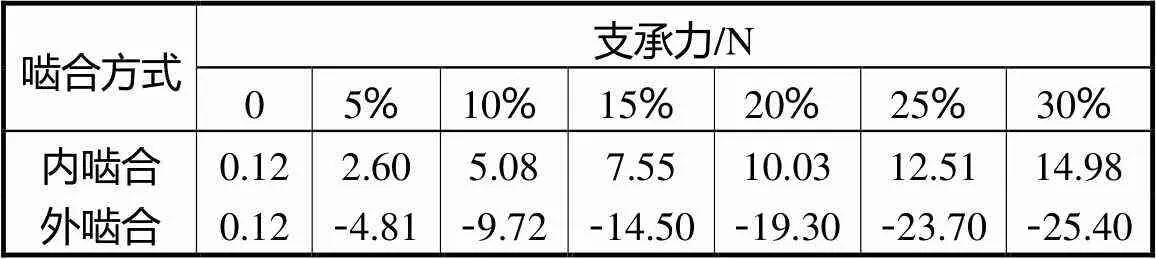
Tab.4 Maximum reaction force of the sun gear along xdirection

在箱体轴承座处施加轴承支承反力，将传动系统的振动特征引入箱体结构，进而分析箱体的振动状态．限于篇幅，仅给出内啮合齿轮副的传动误差间隔相之间存在5%的差异，以及外啮合齿轮副传动误差间隔相之间存在20%的差异时，内齿圈和行星架沿向的径向支承力，如图7和图8所示．

图7 内齿圈沿x向的支承力

图8 行星架沿x向的支承力

2.3 箱体结构的动态响应

如上所述，为仿真箱体的真实振动状态，建立如图9所示的箱体结构有限单元模型．

图9 箱体有限元模型

建模过程如下：①忽略箱体上油孔、倒角等局部结构；②建立箱体结构的三维实体模型，将其导入ANSYSWorkbench瞬态分析模块，并设置端盖与箱体、内齿圈与箱体的材料及其接触构件之间的连接关系，按照传动系统的运行时间设置瞬态分析的载荷步；③对箱体进行网格划分；④底座螺栓孔、箱体底面处设置绑定约束．根据力的作用方向，将各构件的径向支承力以轴承支承反力的形式施加于轴承-轴承座的接触面；⑤求解箱体结构的动态响应．

当太阳轮存在裂纹损伤时，损伤轮齿与行星轮的啮合点位置随行星架旋转而变化．随着行星架旋转，裂纹损伤点与行星轮的啮合位置逐渐远离/靠近传感器，传感器测试到的振动信号逐渐减弱/增强．这一现象可以通过以行星架旋转频率为基频的Hanming窗函数[10]来表示，即

设A1、B1点(如图9所示)为仿真信号采集点，采集A1、B1点的仿真振动信号后，对其进行频谱分析，结果如图10和图11所示．

图11 B1点沿y向的频谱信号

由图10可知，啮合频率m两侧呈现间隔为1/4倍裂纹故障频率crack、行星架旋转频率c(4.22Hz)的调制边带；频率m＋1/4crack两侧呈现间隔为行星架旋转频率c的调制边带，且啮合频率右侧，频率m＋1/4crack＋c比m＋1/4crack－c的频率成分更为明显，啮合频率左侧情况类似．

与图10对比可知，1位置的振动信号包含了与1位置相似的频谱成分，但1点较1点的频谱成分的整体峰值更高．这些现象可以解释为：行星齿轮箱是一个完备的机械系统，行星传动系统的啮合特征必然会影响箱体的振动状态，而啮合频率受到裂纹特征频率和行星架转率的调制，进而呈现3种频率的组合形式；又因1/4crack＋c与太阳轮旋转频率s(19.3Hz)重合，使得m＋1/4crack＋c频率成分更为明显；而1位置比1位置更接近内、外啮合点，导致1点较1点频谱成分的整体峰值更高．由以上分析可知，当行星齿轮个数为时，箱体振动也会呈现与裂纹故障频率1/倍频有关的频率特征，究其原因，各构件的轴承支承反力的激励作用受到行星轮个数的影响，当轴承支承反力施加于轴承座处后，力信号的频谱特征也反映在箱体结构的振动信号中，即表现出以啮合频率为中心、裂纹故障频率的1/分数倍频为间隔的调制边带．

2.4 实验验证

为验证所建模型即参数计算方法的准确性，搭建含太阳轮齿根裂纹损伤的行星齿轮箱动力传动故障诊断实验台．设置采样频率为12800Hz，采样时间为10.24s，其他实验数据与仿真一致．对应仿真信号采集点1、1，实验信号采集点表示为2、2，2、2位置如图12所示．

图12 动力传动系统实验台

采集2、2点的振动加速度信号，并对这一信号进行频谱分析，结果如图13和图14所示．

图13 A2点沿y向的频谱信号

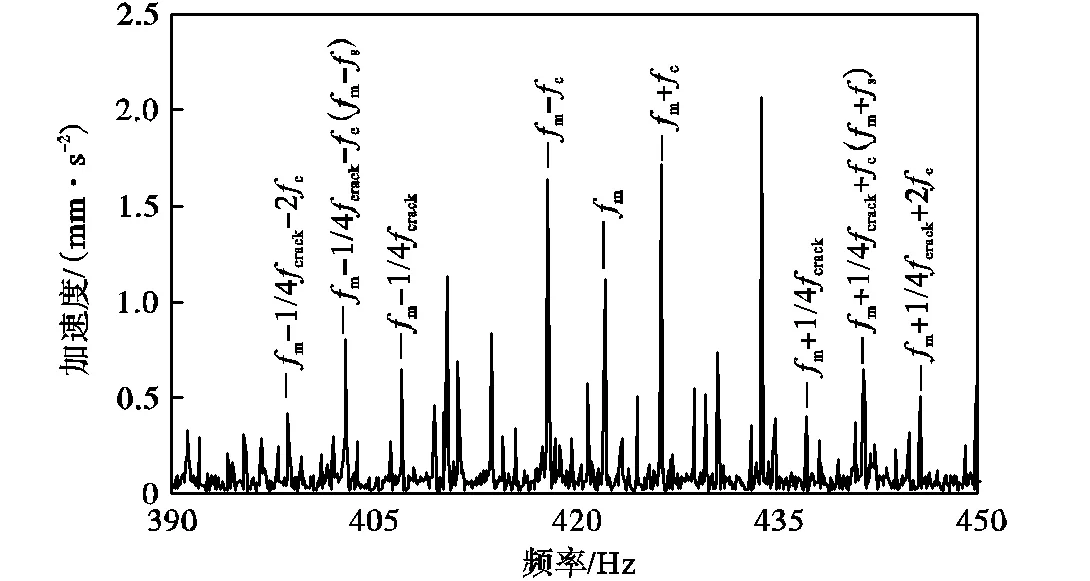
图14 B2点沿y向的频谱信号

由图13、图14可知，实验信号中的主要频率特征成分与仿真信号基本一致．但2、2点还包含1、1点没有的频率成分．究其原因，由于动力传动故障诊断实验台中包括高速级行星齿轮箱和低速级定轴齿轮箱，除上述行星齿轮箱外，定轴齿轮箱中的频率成分在频谱图中也有呈现．尽管如此，上述原因并不影响揭示行星齿轮箱中齿根裂纹损伤的故障机理及振动传动特性．

对比图10与图13、图11和图14可知，当太阳轮存在齿根裂纹损伤时：①在啮合频率两侧均呈现以裂纹故障频率crack的1/4倍频、行星架旋转频率c为间隔的调制边带；②频率m＋1/4crack两侧均呈现间隔为行星架转频c的调制边带，且啮合频率右侧，m+ 1/4crack＋c处的频率成分较m＋1/4crack－c处更为明显，啮合频率左侧情况类似；③1(2)点故障特征较点1(2)更为明显，频谱成分的整体峰值更高．

另外，对比各特征频率处的幅值可以发现，相比于实测信号，仿真信号的啮合频率及其边频成分的峰值较低．其现象可能的原因在于：①行星齿轮箱作为复杂的机械系统，其实体结构与运行工况复杂，而理论模型中计入的影响参数有限，导致仿真结果与实测结果仍有一定差异；②文中内、外齿轮副传动误差间隔相分别存在5%和20%的差异，而被试齿轮箱中的误差激励更为复杂，导致仿真计算的时频响应与实测结果仍存在一定出入．尽管存在特征频率处峰值不一致，但是仿真信号与实验信号各主要频率成分基本一致，据此可以断定所建行星齿轮箱的传动-结构耦合动力学模型及参数计算方法的准确性．因此，本文研究模型可以揭示行星齿轮箱的故障机理和信号传动特性，并应用于后续的故障诊断研究．

3 结 论

(1)建立了含齿根裂纹损伤的行星齿轮箱传动-结构耦合动力学模型．建模过程中，啮合刚度与传动误差的结果表明，齿根裂纹损伤会降低其所在轮齿的啮合刚度，但对传动误差的影响微弱．

(2)传动系统的动力学响应表明，制造及安装误差造成各传动支路不均载，加剧了系统振动，进而使齿根裂纹损伤引起的啮合冲击被淹没．

(3)有限元仿真结果与实验结果均表明，所建动力学模型能够正确揭示行星齿轮箱的故障机理，而故障特征与行星轮个数相关．具体表现为频谱图中存在以啮合频率为中心、裂纹故障频率的1/分数倍频及行星架旋转频率为间隔的调制边带．

(4)与仿真信号对比表明，实测信号中，各阶次谐波的能量分配关系较理论仿真信号更为复杂，这一问题后续将通过细化动力学模型做进一步研究．

［1］ Cooley C G，Parker R G. A review of planetary and epicyclic gear dynamics and vibration research[J]. Applied Mechanics Reviews，2014，66(4)：1-15.

［2］ Lei Y G，Lin J，Zuo M J，et al. Condition monitoring and fault diagnosis of planetary gearboxes：A review[J]. Measurement，2014，48(1)：292-305.

［3］ Wan Z G，Cao H R，Zi Y Y，et al. An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack[J]. Engineering Failure Analysis，2014，42(5)：157-177.

［4］ 马 锐，陈予恕. 含裂纹故障齿轮系统的非线性动力学研究[J]. 机械工程学报，2011，47(21)：84-90.

Ma Rui，Chen Yushu. Nonlinear dynamic research on gear system with cracked failure[J]. Chinese Journal of Mechanical Engineering，2011，47(21)：84-90(in Chinese).

［5］ 符升平，李胜波，罗 宁，等. 车辆变速器齿轮轴系和箱体动力学耦合研究[J]. 汽车工程，2016，38(9)：1186-1194.

Fu Shengping，Li Shengbo，Luo Ning，et al. A research on dynamics coupling between gear shafts and housing in a vehicle transmission[J]. Automotive Engineering，2016，38(9)：1186-1194(in Chinese).

［6］ 贺朝霞，常乐浩，刘 岚. 耦合箱体振动的行星齿轮传动系统动态响应分析[J]. 华南理工大学学报，2015，43(9)：128-134.

He Zhaoxia，Chang Lehao，Liu Lan. Dynamic response analysis of planetary gear transmission system with coupled gearbox vibration[J]. Journal of South China University of Technology，2015，43(9)：128-134(in Chinese).

［7］ 任亚峰，常 山，刘 更，等. 箱体柔性对齿轮传动系统动态特性的影响分析[J]. 振动与冲击，2017，36(14)：87-91.

Ren Yafeng，Chang Shan，Liu Geng，et al. Influence of housing flexibility on the dynamic characteristics of gear transmission systems[J]. Journal of Vibration and Shock，2017，36(14)：87-91(in Chinese).

［8］ 任亚峰，常 山，吴立言，等. 齿轮-箱体-基础耦合系统的振动分析[J]. 华南理工大学学报，2017，45(5)：38-44.

Ren Yafeng，Chang Shan，Wu Liyan，et al. Vibration analysis of gear-housing-foundation coupled system[J]. Journal of South China University of Technology，2017，45(5)：38-44(in Chinese).

［9］ 雷亚国，罗 希，刘总尧，等. 行星轮系动力学新模型及其故障响应特性研究[J]. 机械工程学报，2016，52(13)：111-122.

Lei Yaguo，Luo Xi，Liu Zongyao，et al. A new dynamic model of planetary gear and research on fault response characteristics[J]. Chinese Journal of Mechanical Engineering，2016，52(13)：111-122(in Chinese).

［10］ 雷亚国，汤 伟，孔德同，等. 基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[J]. 机械工程学报，2014，50(17)：61-68.

Lei Yaguo，Tang Wei，Kong Detong，et al. Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis[J]. Chinese Journal of Mechanical Engineering，2014，50(17)：61-68(in Chinese).

［11］ Liang X H，Zuo M J，Liu L B. A windowing and mapping strategy for gear tooth fault detection of a planetary gearbox[J]. Mechanical Systems and Signal Processing，2016，80(1)：445-459.

［12］ Liang X H，Zuo M J，Hoseini M R. Vibration signal modeling of a planetary gear set for tooth crack detection[J]. Engineering Failure Analysis，2015，48：185-200.

［13］ Inlpolat M，Kahraman A. A dynamic model predict modulation sidebands of a planetary gear set having manufacturing errors[J]. Journal of Sound and Vibration，2010，329(4)：371-393.

［14］ Liu X Z，Yang Y H，Zhang J. Resultant vibration signal model based fault diagnosis of a single stage planetary gear train with an incipient tooth crack on the sun gear[J]. Renewable Energy，2018，122：65-79.

［15］ Sainsot P，Velex P，Duverger O. Contribution of gear body to tooth deflections—A new bidimensional analytical formula[J]. Journal of Mechanical Design，2004，126(4)：748-752.

［16］ Ma H，Pang X，Feng R J，et al. Improved time-varying mesh stiffness model of cracked spur gears[J]. Engineering Failure Analysis，2015，55：271-287.

［17］ Parker R G，Lin J. Meshing phasing relationships in planetary and epicyclic gears[J]. Journal of Mechanical Design，2004，126(2)：525-534.

［18］ Chen Z，Shao Y. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism & Machine Theory，2013，62(4)：63-74.

［19］ 张 俊，宋轶民. NW型直齿行星传动的动力学建模与固态特性分析[J]. 天津大学学报，2011，44(8)：677-682.

Zhang Jun，Song Yiming. Dynamic modeling and eigenvalue of NW spur planetary gear unit[J]. Journal of Tianjin University，2011，44(8)：677-682(in Chinese).

［20］ Ma H，Zeng J，Feng R J，et al. An improved analytical method for mesh stiffness calculation of spur gears with tip relief[J]. Mechanism & Machine Theory，2016，98：64-80.

Investigation of Fault Mechanism of a Planetary Gearbox with Incipient Tooth Crack

Zhang Jun1，Li Xike1，Wang Jian1，YaoLigang1，Liu Xianzeng2

(1. School of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350116，China；2. School of Mechanical Engineering，Tianjin University，Tianjin 300350，China)

Identifying weak fault features caused by an incipient tooth crack in a planetary gearbox is difficult．To characterize the fault features ofincipient tooth cracks in a planetary gear train，this paper established a transmission-structure-coupled nonlinear dynamic model that includes the effect of crack damage with lumped parameter method．Based on potential energy method，a mathematical model of time-varying mesh stiffness and transmission error was established．The effect of crack damage was incorporated into the nonlinear dynamic transmission model through stiffness excitation and displacement excitation functions．Furthermore，the vibration response of the planetary transmission system was solved，indicating that the difference in transmission error between internal and external transmission branches is an important cause of non-uniform load distribution．Moreover，a finite element model of the gearbox was built in the ANSYS Workbench environment．After applying the reaction forces of the sun gear，the carrier and the ring gear on the bearing housings of the gearbox，and including the modulation effect of the carrier rotation with a window function，frequency analysis can be conducted on the simulated vibration signals to identify the damage mode of the tooth crack．Finally，a test rig of the planetary gearbox was constructed，based on which a set of vibration tests were conducted to detect the tooth crack．The consistencies of the simulated and experimental signals prove that the proposed transmission-structure-coupled dynamic model can accurately reveal the fault mechanism of the planetary gearbox with an incipient tooth crack．The fault features of this planetary gearbox demonstrate a set of modulated sidebands around the mesh frequency．Additionally，the intervals of the modulated sidebands are the fractional frequencies doubling of the fault frequency and carrier rotation frequency．

planetary gearbox；incipient tooth crack；fault features；modulated sidebands

TH132.4

A

0493-2137(2019)11-1117-12

10.11784/tdxbz201812035

2018-12-19；

2019-01-27.

张 俊（1981—  ），男，博士，教授.

张 俊，zhang_jun@fzu.edu.cn.

国家自然科学基金资助项目(51875105，51375013).

Supported by the National Natural Science Foundation of China(No.51875105，No.51375013).

(责任编辑：金顺爱)