大girth多进制阵列准循环LDPC码

刘 冰 任席闯 崔 洁

（中国人民解放军91469部队 北京 100841）

1 引言

1998年，Davey和Mackay重新发现了多进制LDPC（Low-DensityParity-Check）码［1］，并提出了用于译码的多进制和积算法（Q-arySum-ProductAlgorithm，QSPA），相比于二进制LDPC码来说取得了明显的编码增益，多进制LDPC码的出现为LDPC码的研究开拓了一个新的领域，也有许多关键问题亟待进一步研究。多进制LDPC码除了具备二进制LDPC码的一般特性外，还具有独特的优势，如当码长较短时具有更好的纠错能力，更强的抗突发错误能力，且适合高速率传输系统。

Tanner图中环的大小和分布是影响多进制LDPC码性能的重要因素之一，特别是短环的存在会破坏变量节点和校验节点信息传递的独立性假设，使相关信息在两类节点之间传递，影响码字的迭代收敛过程，造成译码性能急剧下降。一般构造码字之初就会考虑消除4环，而且此类研究成果已经非常丰富［2～5］。Tanner图中最短环的长度称之为 girth（围长）。小girth（最小环）会对低码率、长度较短的码字影响较大，消除这类码的短环或减少其分布可以带来明显的性能改善。另一方面，Tanner图的girth还与码的最小距离有关，一般girth越大，最小距离也将随之增大，但最小距离并不随girth增大而无限增大，一味地增大girth并不能提高码字的性能［6］。因此，构造大girth（girth≥8）的多进制LDPC码是多进制LDPC码的一个研究方向。

对于迭代译码的准循环（Quasi-Cyclic，QC）LDPC码来说，短环的存在不利于算法的收敛，性能损失的一部分原因归咎于小girth的存在。目前，大多数构造方法都考虑了消除4环，即girth至少为6。构造出girth为8，甚至更大girth且具备低复杂度的多进制QCLDPC码是当前的研究热点之一［7～10］。构造大girth的主要方法有直接构造法和短环删除法，其中直接构造法是根据设计的规则使得校验矩阵达到大girth的特性。本文从大girth指数矩阵出发，提出了在不同域上广义多进制位置向量和广义二维扩展方法，采用直接构造法确定短环线性约束方程，与大girth阵列码结合构造出了大girth多进制阵列LDPC码。

2 大girth多进制准循环LDPC码

2.1 大girth指数矩阵构造

阵列码是一种准循环的LDPC码，其校验矩阵是由许多个的循环置换矩阵阵列所组成，形式为

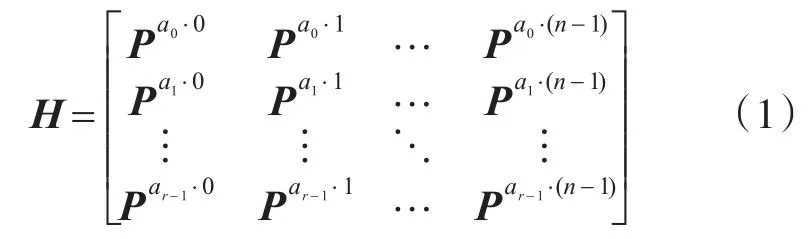
其中，P是大小为 p×p的循环置换阵，p为素数，阵列行序号 a0，a1，…，ar-1是取值范围为 [0，p-1]的不同整数。H的指数矩阵定义为

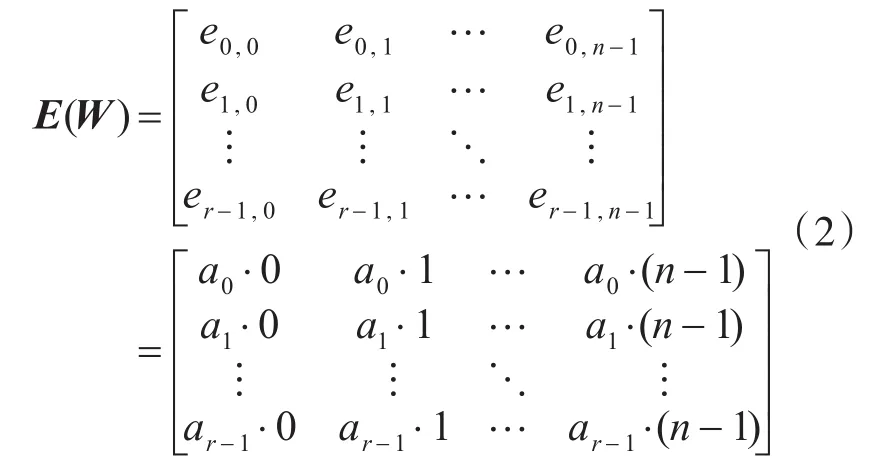
其中，ei，j=ai·j，0≤i≤r-1，0≤j≤n-1，W 表示校验矩阵H 的基矩阵。如果序列a0，a1，…，ar-1形成 等 差 数 列 ，即 对 于 i=0，1，…，r-2 ，ai+1-ai=d≠0，称对应的码为等差阵列码。如序列a0，a1，…，ar-1未形成等差数列，则称之为非等差数列码。

校验矩阵girth的控制主要放在指数矩阵层面上。任何奇偶校验矩阵H中长度为2i的闭环可形成阵列行和阵列列的序号对(r0，n0)，(r0，n1)，(r1，n1)，(r1，n2)， …，(ri-1，n0) ， 其 中 ，rk≠rk+1，nk≠nk+1，ri-1≠r0， ni-1≠n0，k=0，1，…，i-1。通过闭环可得到一个重要的定理。

定理1［4］：矩阵 H 对应的Tanner图的girth至少为2(i+1)充要条件是

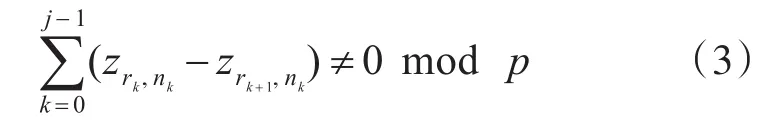
其中，2≤j≤i，0≤rk，rk+1≤m-1，0≤nk≤n-1，且r0=rr，rk≠rk+1，nk≠nk+1。 可 见 ，要 使 得girth≥2(i+1)，必须消除Tanner图中环长小于或等于2i的环。对于阵列码来说，由于存在r0，r1，n0，n1，r0≠r1，n0≠n1，则 (ar0-ar1)(n0-n1)≠0 ，进而得，根据定理1可知阵列码的girth至少为6。

考虑校验矩阵girth为8和10的两种情况，列重分别选取3和4。对于等差阵列码，由式（3）可化为

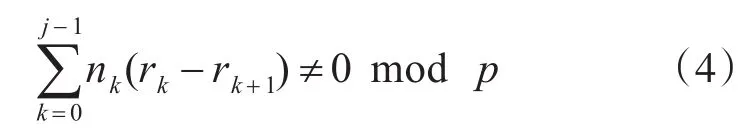
为了得到大girth，要尽量消除短环或减少短环的数量。首先对等差阵列码进行分析，考虑girth为8的情况，由于阵列码不存在4环的情况，只需从去除6环开始考虑。首先确定6环存在的条件。如果行重 r=3 ，阵列行序号 r0，r1，r2∈{0，1，2} ，由于r0，r1，r2，n0，n1，n2互不相等，存在6环的阵列列选择必定位于不同阵列列的序号上。不失一般性，取r0=0，r1=1，r2=2，由定理1可得如表1所示第一行存在6环的约束方程，只要在校验矩阵H选取的序列中，避免存在满足约束方程的序列即可消除相应的环长。

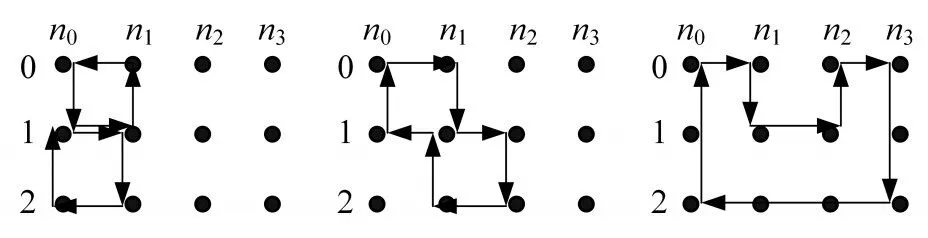
图1 存在8环的示例

对于表1中约束方程的计算，以存在8环，行重为 3 的 情 况 为 例 ，由 于 r0，r1，r2，r3∈{0，1，2} ，n0≠n1，n1≠n2，n2≠n3，n3≠n0，n0，n1，n2，n3是两两不相同的，因而矩阵中存在的环路需分3种情况：列号取值范围分别为2列、3列和4列。对应的示例图如图1所示。

表1 6环和8环存在的约束方程和避免6环和8环的列序列

对于2列的情况，假设n0=n2，n1=n3，存在8环的约束方程为

由于n0≠n1，满足约束方程的充要条件是r0-r1+r2-r3=0。当 r0=0，r1=1，r2=2，r3=1时，其充要条件r0-r1+r2-r3=0总是会满足的。在2列的情况下，这种8环是无法避免的。

对于3列的情况，可假设n0=n2或n1=n3，不失一般性，这里仅考虑n0=n2。存在8环的约束方程为

n0(r0-r1+r2-r3)-n1(r1-r2)+n3(r3-r0)=0（6）

由于阵列行序号 r0，r1，r2，r3∈{0，1，2}，表2给出了3列情况下存在8环不重复的约束方程。

表2 列数为3存在8环的约束方程

对于4列的情况，存在8环的约束方程为n0(r0-r1)+n1(r1-r2)+n2(r2-r3)+n3(r3-r0)=0（7）

由于阵列行序号 r0，r1，r2，r3∈{0，1，2}，表3给出了4列情况下存在8环不重复的约束方程。

表3 列数为4存在8环的约束方程

对于其他情况，分析方法与存在8环，行重为3的情况是类似的。具体的环约束方程和避免相应环的部分可选取序列如表1所示。

从上述分析可知，等差阵列码的girth不会大于8，在两个阵列列中，当r0=0，r1=1，r2=2，r3=1时，8环是不可避免的。而采用非等差数列码可以在两个不同的阵列列中避免这种8环的存在。

对于非等差数列码，式（3）变为

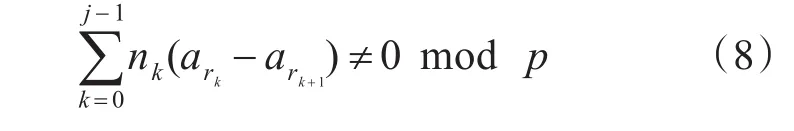
如同等差数列码的分析，对于2列的情况，假设n0=n2，n1=n3，存在8环的约束方程为

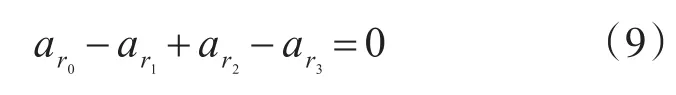
由于 ar0，ar1，ar2，ar3的集合域不在等差数列范围内选取，因而会带来一些优势和问题：选择的范围扩大，环约束的方程相应增多，搜索序列的复杂度会相应增加；可得到girth为10或12这样更大girth的码字。其分析与大girth等差阵列码中寻求阵列序列方式相同，如表4所示给出了列重为3、阵列行序号 ar0，ar1，ar2，ar3∈{0，1，3}、环长为 6和 8的约束方程以及避免相应环的列序列。

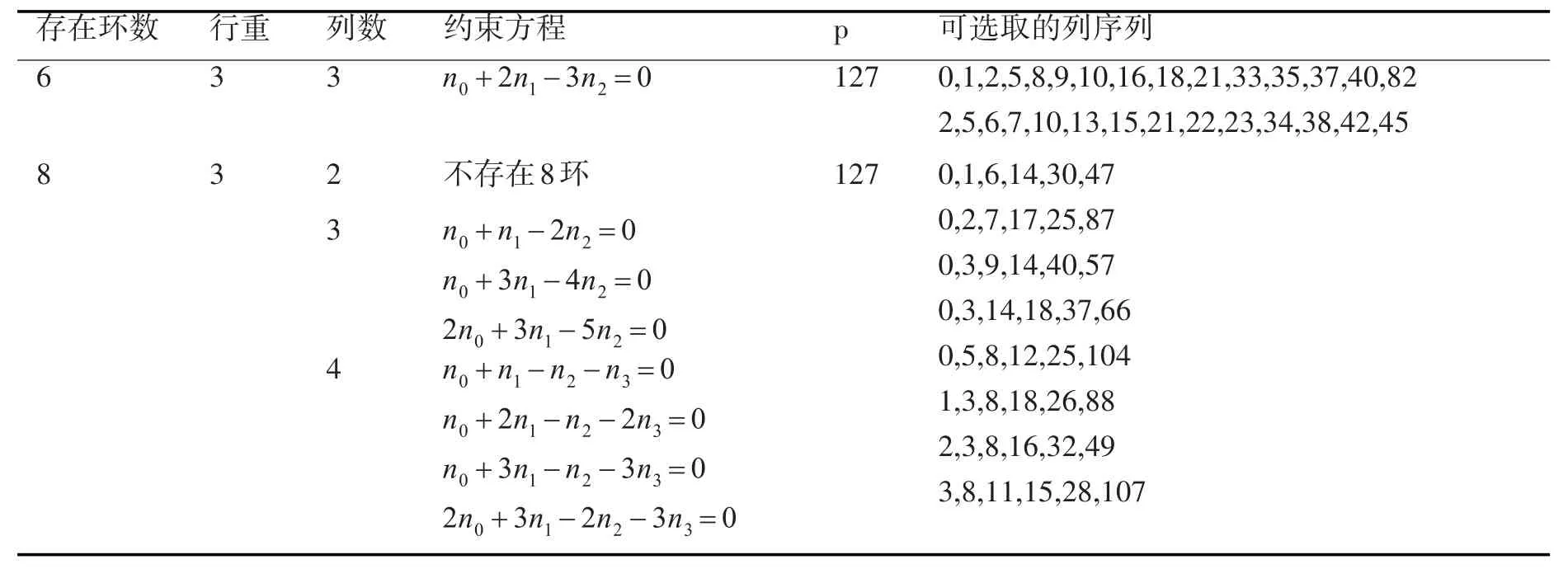
表4 非等差数列码6环和8环存在的约束方程和避免6环和8环的列序列

2.2 大girth多进制阵列码

根据上节约束关系选出的指数矩阵E(W)，可以保证多进制奇偶校验矩阵H的girth都为8和10，分别避免了环长6和8。也可产生出更大girth的校验矩阵，只是选取列序列受控的约束方程会更多，搜索的难度增大。无限增大girth最终对性能的提高也不会太大，并且阵列码无法避免长度为12的环［11］。

对于多进制阵列LDPC码校验矩阵的构造将从指数矩阵E(W)出发进行扩展，且循环阵中不存在零阵。广义多进制扩展方法基于两个不同域：GF(p)和GF(2l)。多进制LDPC码校验矩阵非零值的位置由GF(p)域决定，非零值的数值由GF(2l)域决定。这两个域的具体关系如下：(2l-1)·(rt-1)＜p＜(2l-1)·rt，其中，l∈Z，rt=

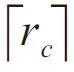
为GF(2

l

)域中所有非零元素重复的周期数，不足一个周期的，记为一个周期，并计入r

t

中，r

c

是重复周期的带分数表示，整数部分表示的是重复的整数周期数，分数中分母表示一个周期的长度，分子表示不足一个周期的剩余长度。l与 p值的具体关系由下式表示：

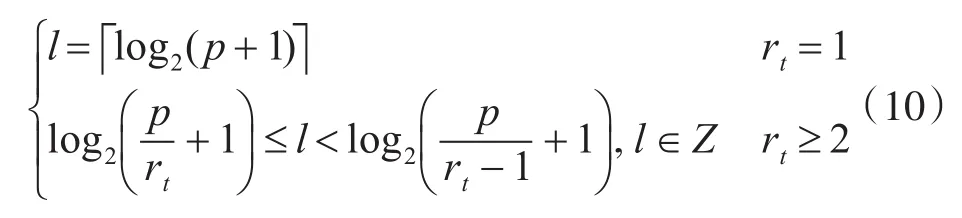
其中，

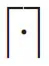
表示向上取整。

广义二维扩展包括水平扩展和垂直扩展。首先给出水平扩展的方式，即为提出的广义多进制位置向量。令 β是GF(2l)域的本原元。将基于GF(p)和GF(2l)域的广义多进制位置向量定义为z(I)=(z0，z1，…，zp-1)，其中 zi=βimod(2l-1)，i∈I ，其它所有分量为0。集合I是广义多进制位置向量中非零值所在的位置序号，多进制位置向量的重量等于集合I的势Card(I)。定义向量的数值取值范围是GF(2l)域中的2l-1个非零元素。当 z(I)是GF(2l)域上重量为1的 p重向量时，构造出校验矩阵的子阵列为广义循环置换矩阵，此时矩阵的非零位置数由指数矩阵决定；当z(I)是GF(2l)域上重量不为1的 p重向量时，构造出校验矩阵的子阵列为广义循环矩阵，此时非零位置数将由一个集合来决定。接着给出垂直扩展方式。令I是任一由GF(p)域中的元素组成的集合，广义多进制位置向量z(I+1)定义为位置向量z(I)向右循环移一位，移位后第1列至第 pm-1列的元素乘以β分别得到第2列至第 p列元素，而第 p列元素则乘以βrt(2l-1)-(p-1)后得到第1列元素。根据广义多进制位置向量的扩展规则，多进制位置向量z(I+γ)定义为集合I中元素依次加γ∈GF(p)后扩展得到的广义多进制位置向量，在GF(2l)域上可形成以I，I+1，…，I+p-1的广义位置向量为行的多进制p×p大小的循环矩阵PI。

二维 p重扩展可由上述垂直扩展和水平扩展两部分组成，对于任一集合 I，dispv(I)=[I，I+1，…，I+p-1]T为该集合的垂直扩展，而disph(I)=z(I)为该集合的水平扩展，其中无论集合I中元素取GF(p)域内何值，循环矩阵PI都不会为全零矩阵。集合I与循环置换矩阵PI是一一对应的关系：

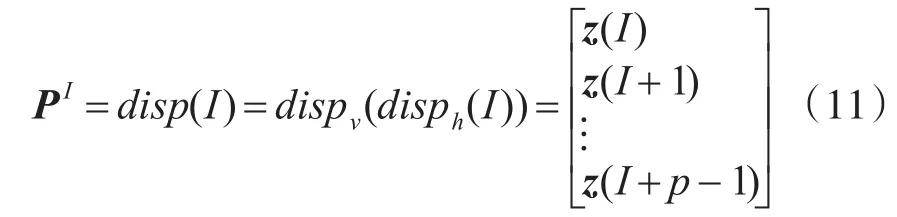
通过式（11）可从指数矩阵（对应于广义循环置换矩阵）或相应集合（对应于广义循环矩阵）构造出具有广义循环特性的多进制校验矩阵H。由于多进制校验矩阵非零值位置和数值的选取分别建立在GF(p)和GF(2l)两个不同的域上，构造出的二维 p重矩阵PI非零元素的分布具有两种情形：1）当rt=1时，在GF(2l)域上只具有部分域元素循环（rc＜1）或循环（rc=1）的特性；2）当 rt≥2时，所有GF(2l)域非零元素个数一般在矩阵中分布不均，但是当2l-1=rcp时，非零元素分布将是均匀的。为了便于表示，PI简化记为 Hi，j，由扩展的性质知Hi，j是广义循环矩阵，因此其可分解为一个非奇异的对角矩阵Y和一个循环矩阵之积。将 Hi，j表示为两个 p×p矩阵Y和的 乘 积 ，即，其中是一个 GF(2l)域上不具有乘 β性质的移位循环矩阵，如果单独来看，它是一个二进制矩阵，非零元素取值选自GF(q)域中的某个非零值，Y是一个以部分周期循环元素β0，β，…，β2l-2，β0，β，… 为主对角线，其余为 0 的p×p大小的方阵，记为Y=diag(β0，β，…)。设 c为码字向量，则，可知，与是等价的。所以说，矩阵和的零空间给出的码字是一样的。因此，通过可以找到具有系统或部分系统形式的生成矩阵，以实现有效的线性复杂度编码［10］。可以说通过广义位置向量扩展生成的多进制LDPC码充分考虑了编码和译码的实现复杂度，在编码上，由于校验矩阵是广义QC形式的矩阵，继承了QC矩阵的特性，可采用QCLDPC码的有效编码方法；在译码上，通过广义二维扩展，数值域建立在2的幂次上，使得译码可以采用高性能低复杂度的软判决译码算法，利于工程应用。

3 仿真结果及性能分析

本节将对构造的大girth多进制阵列LDPC码进行仿真比较，仿真中的信号均采用BPSK调制，且在双边功率谱密度为N02的AWGN信道中传输。译码采用FFT-QSPA算法且最大迭代次数设置为50，仿真中的误码率是在检测50帧错误的条件下得出的。为了便于比较，对于等差阵列码和非等差阵列码，取 p=127，其子阵列的大小为127×127，选择的列重都为3，行重都为6，因此，r=3，n=6。根据码的性质、girth和等差阵列码的数值域选择的不同构造出8种不同的多进制LDPC码。在构造出的LDPC码中，从构造性质的角度，有等差阵列码和非等差阵列码；从girth的角度，有girth为8和10的码；从数值构造域的角度，有128进制、64进制和32进制LDPC码。

仿真中等差阵列码阵列行序号选{0，1，2}，非等差阵列码阵列行序号选{0，1，3}。girth大小的选择按照表1和表4中给出的序列来抽取指数矩阵中相应的列。对于数值域GF(2l)选择如下：当l=7时，rt=1，rc=1，此时矩阵中元素分布是均匀的；当 l=6时，rt=3，；当 l=5时，rt=5，。根据三种GF(2l)域选择构造出不同的多进制LDPC码，但是选择的指数矩阵都是相同的。等差数列情况，R3G8码（3表示列重，8表示girth值）的指数矩阵为

R3G10码的指数矩阵为

非等差数列情况，R3G8码的指数矩阵为

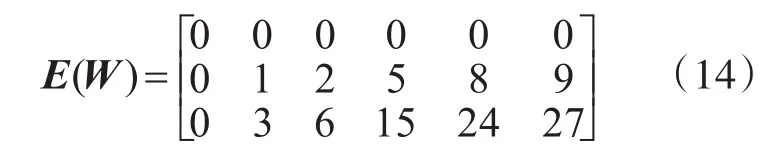
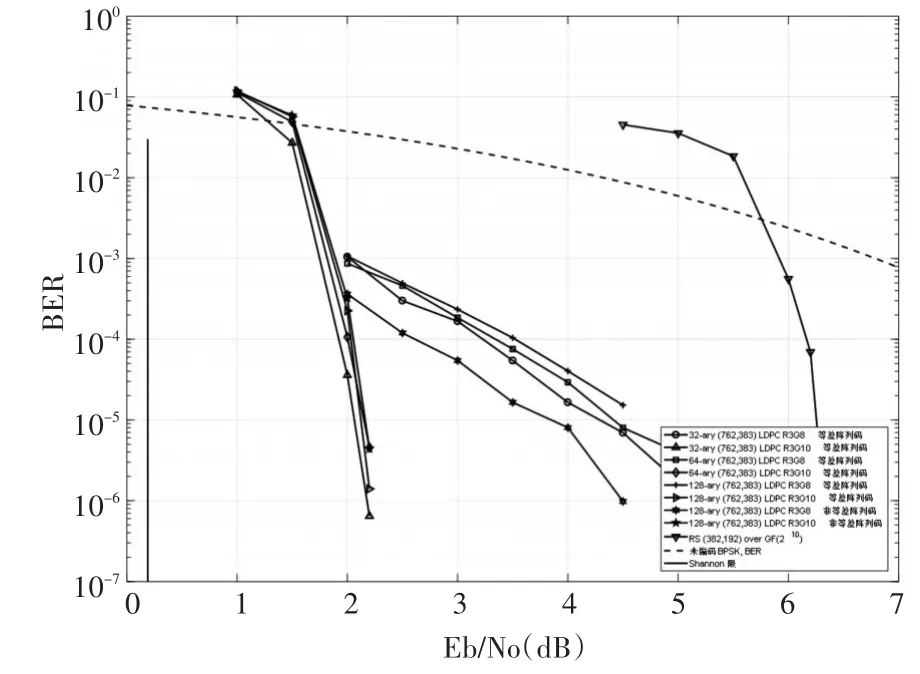
图1 不同参数的多进制（762，383）阵列LDPC码的误码性能比较

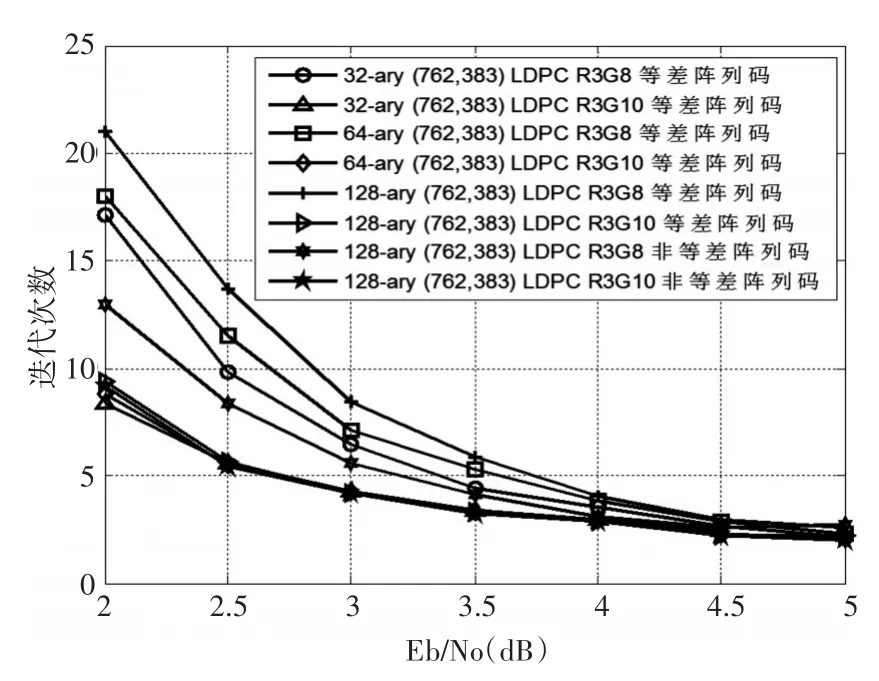
图2 不同参数的多进制（762，383）阵列LDPC码的迭代性能比较

R3G10码的指数矩阵为

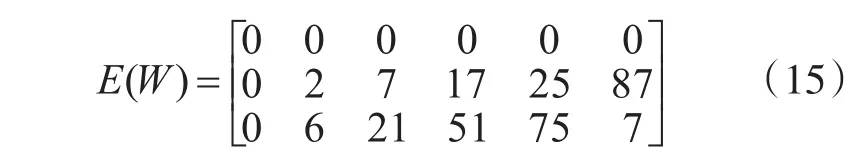
8种多进制（762，383）阵列LDPC码的误码性能和迭代性能分别如图1和图2所示。其中等差阵列R3G10码是存在8环的，但是通过列阵列的选取还是可以消除大部分存在的8环。为了便于比较，图1也给出了RS码BM算法的误码性能，在误比特率（BitErrorRate，BER）为 10-5处，32进制（762，383）R3G8LDPC 码相对于 GF(210)域（382，192）RS码来说，取得了大约4.24dB的编码增益。从图1和图2还可以得出：1）非等差阵列码在girth为8时取得的性能优于等差阵列码，但是girth为10时，其优势就不太明显了；2）尽管有的码只是部分消除了8环，但是girth为10的码比girth为8的码取得了更大的编码增益；3）等差阵列码中，随着进制数的减少，其性能越好，收敛越快，但是之间的差距并不大。进制数的减少同时也能降低译码的复杂度。对于结论3）这种现象Mackay也曾指出［1，12］：随着域阶数的增加，其误码性能并不总是单调提升，这一现象的产生与校验矩阵的构造密切相关。

下面考虑列重为4的大girth多进制LDPC码的性能。参数选取如下：p=509，l=6，这样构造出的广义多进制准循环校验矩阵位置和数值的选择分别基于GF(509)和GF(64)域，列重为4，行重为8，子阵列的大小为 509×509，rt=9，。

R4G8码的指数矩阵为

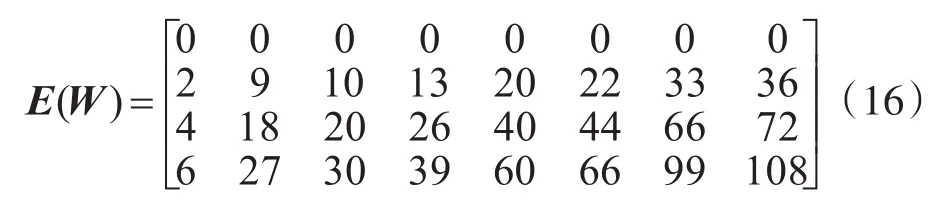
R4G10码的指数矩阵为

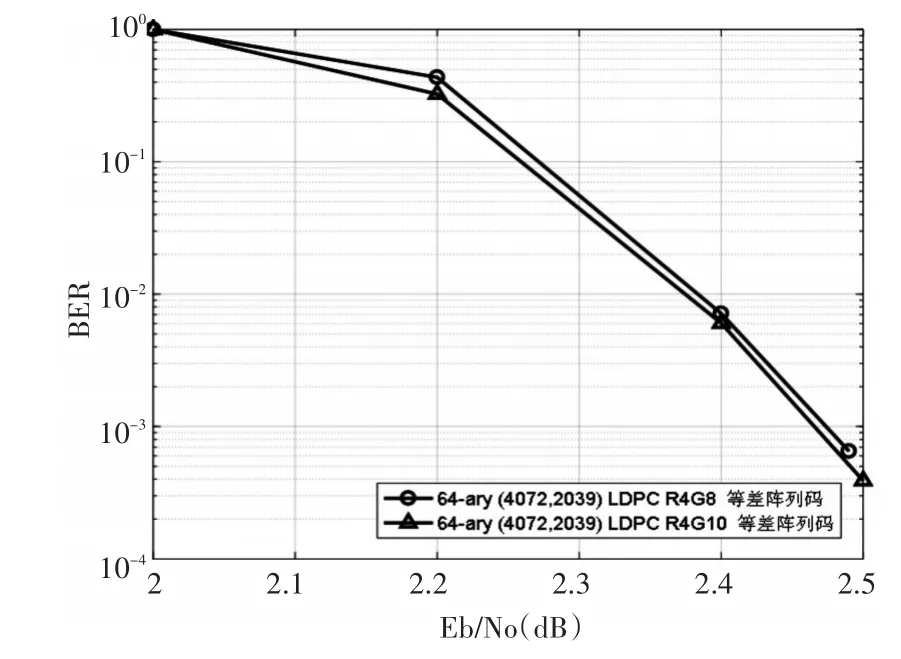
图3 64-ary（4072，2039）阵列LDPC码的误码性能曲线

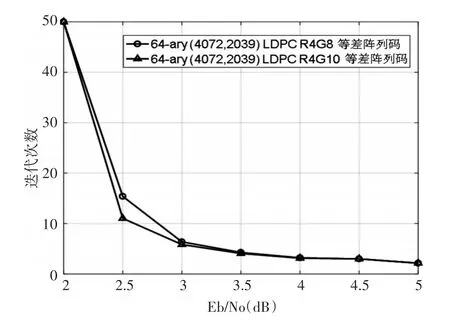
图4 64-ary（4072，2039）阵列LDPC码的迭代性能曲线

由上述两个指数矩阵构造的校验矩阵大小都为2036×4072矩阵的秩同为2033，其零空间给出了码率为0.5007的64-ary（4072，2039）阵列LDPC码，其误码性能和迭代性能分别如图3和图4所示。从仿真结果来看，girth为10的码取得性能略优于girth为8的码。

4 结语

大girth及其分布是保证码字性能的一个重要因素之一。为了构造大girth多进制LDPC码，从指数矩阵出发，选出避开短环的阵列列，并将广义二维扩展方法应用于指数矩阵，构造出不存在短环的校验矩阵。仿真结果表明，基于广义二维扩展方法的多进制大girth阵列LDPC码能取得良好的性能，利于有效的编译码，可减少存储空间。构造出的校验矩阵在一定程度上增大girth能明显提高码字的性能，保证信息的可靠传输，满足无线通信的高频带利用率。