基于预测函数控制的水面无人船航向控制器设计
2019-08-05夏云鹏杨田田
夏云鹏 杨田田
(1.中船重工第七一三研究所 郑州 450000)(2.武汉理工大学 武汉 430070)
1 引言
水面无人船是构建海洋智能体系的重要组成部分。随着无人船智能控制技术的发展,无人船在海事领域中的应用也越来越广泛[1]。无人船在推进海事智能管理、提高海洋搜救应急成功率等方面都有重要的应用价值。
模型预测控制(MPC)算法因其先预测后控制的思想,使得其对于被控对象的控制响应更加敏感,能够更快地针对外部扰动变化调整控制动作;同时控制动作产生于其内部优化控制器的在线优化过程,进一步提高了控制系统对被控对象存在的不确定性的处理能力[2~4]。预测函数控制被称为第3代MPC,其保留了MPC的基本特征,并加入对控制输入进行结构化的步骤,将控制量分解为基函数的线性组合,提高控制输入的规律性,降低算法参数在线计算量。依据MPC的上述特点,模型预测控制算法在无人船航向控制领域极具应用价值。水面无人船本身存在操舵约束,其航行过程中还存在风浪流等扰动,针对上述问题,本章采用预测函数控制算法设计无人船航向控制器,实现对航向的有效控制,并为间接航迹控制算法的设计提供支撑[5]。
2 基于经典PID算法的航向控制器
经典PID控制算法设计结构简单,在工程上已获得广泛的应用。图1表示了基于经典PID算法的无人船航向控制系统。无人船航向控制系统为典型的负反馈系统,其输入信号为无人船的目标航向角ψd,输出信号为无人船的实际航向角ψ;PID航向控制器的输入信号为无人船目标航向角ψd与实际航向角之间的偏差,输出信号为无人船的舵角控制量。
如图1所示,基于经典PID算法的无人船航向控制器包括比例、积分和微分三个环节。基于经典PID算法的无人船航向控制器的输出信号与输入信号之间的关系,可用式(1)表示。
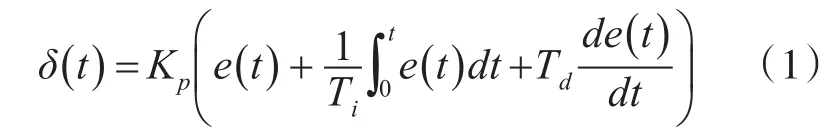
在进行控制器设计时,为方便分析和整定参数,一般令 Ki=KpTi,Kd=Kp*Td,进一步改写式(2)为
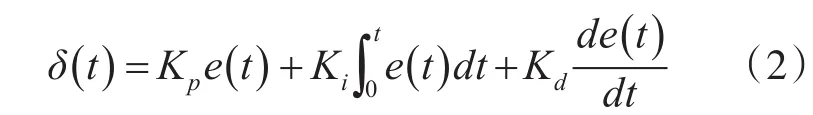
其中,Kp为比例系数,Ki为积分系数,Kd为微分系数。
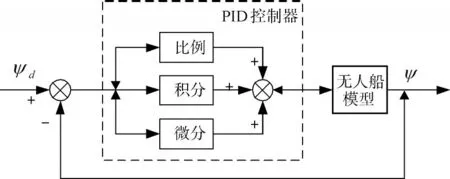
图1 基于PID的无人船航向控制系统框图
3 基于预测函数控制的航向控制器
基于预测函数控制(PFC)的水面无人船航向控制系统总体框图如图3所示。其中,航向控制系统的输入信号为无人船的目标航向角ψd,航向控制系统的输出信号为无人船的实际航向角ψ,基于预测函数控制的航向控制器的输入信号为无人船的目标航向角ψd和无人船的实际航向角ψ,基于预测函数控制的航向控制器的输出信号为无人船的输入舵角控制量δ。水面无人船航向控制系统中的预测函数控制器的控制过程主要包括以下几个步骤:
1)无人船预测模型根据当前舵角控制量计算预测时域内的无人船航向角预测输出值。
2)根据无人船的当前实际航向角输出与预测输出值的偏差对预测时域内的预测输出值进行校正。
3)优化控制器根据优化性能指标函数以及当前无人船的目标航向来计算控制时域内无人船舵角控制量的最优控制序列,并根据计算出的无人船舵角控制量的最优控制序列确定当前时刻施加于无人船上的舵角控制信号。
4)采用滚动优化策略持续上述计算过程(如图2),重复步骤1)~3)。
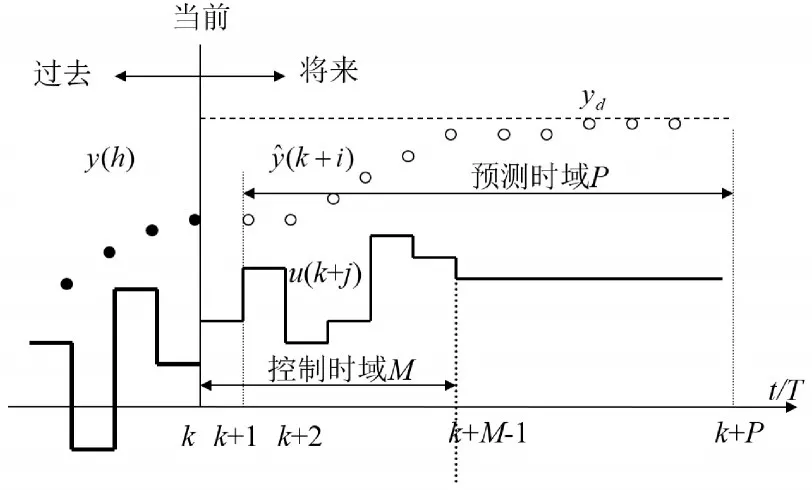
图2 预测控制基本思想
根据以上控制过程,该航向控制器的设计主要涉及无人船预测模型的确定、优化性能指标的确定、反馈校正策略的制定以及预测时域和控制时域的参数选择几个方面。下面将从这几个方面具体介绍基于预测函数控制的无人船航向控制器的设计过程。
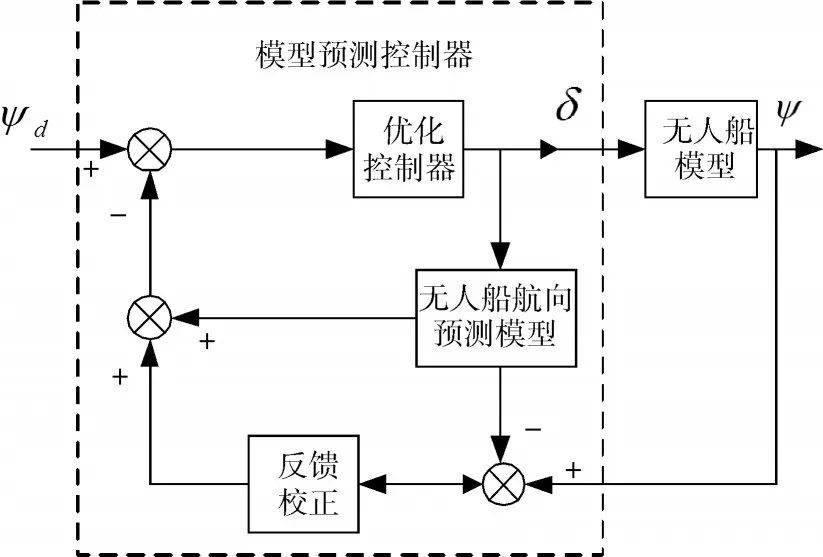
图3 基于PFC的无人船航向控制系统框图
3.1 预测模型
无人船航向控制系统的预测模型是指能够正确描述航向控制系统输入和输出关系的模型。在进行无人船航向控制研究时,采用能够描述无人船操纵性特点的野本方程作为预测模型。野本方程表示为

其中,K表示无人船的旋回性指数,T表示无人船的追随性指数。δ为无人船的舵角;ψ为无人船的艏向角。
取采样时间为Ts,对方程式(3)进行离散化,可得无人船预测模型的差分方程式表示为
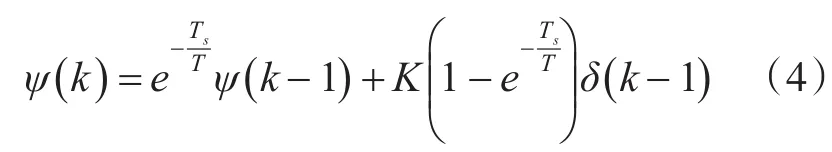
在方程式(3)中,无人船的旋回性指数K和无人船的追随性指数T可以通过对已有实验船进行10°10°的Z形操纵性试验来获得。本文中的实验船的基本参数如表1所示。
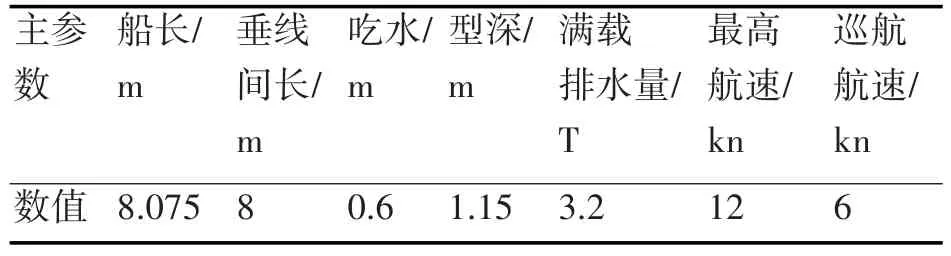
表1 无人船主要参数
在平静的湖面进行了实验船的Z形(10°10°)试验,获得的实验船艏向角和舵角关系变化曲线如图4所示,根据文献[6]中提到的计算方法,对无人船试验数据进行拟合,求得实验船的K、T参数的值为K=0.49,T=1.94。
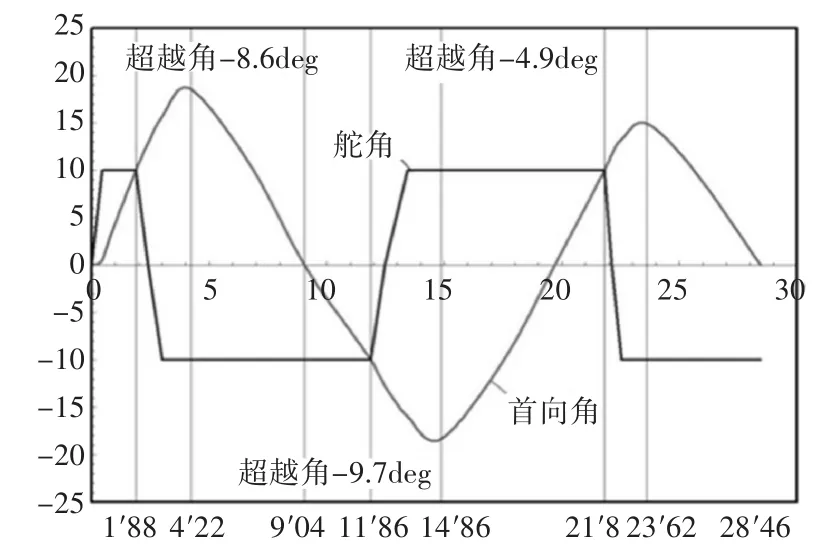
图4 10°10°Z形操纵试验结果
无人船在海上航行时容易受到风、浪的干扰,将这些干扰 fa等效成舵角干扰添加到预测模型中,即将式(3)改写为
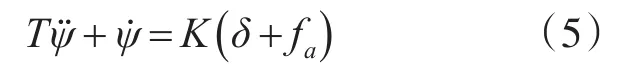
3.2 反馈校正
基于预测函数控制(PFC)的无人船航向控制器中的反馈校正环节主要是对无人船预测模型给出的预测时域内的航向预测输出值进行校正,以使其预测值更接近实际输出值。此处采用k时刻已知无人船预测模型的预测输出航向角ψm()k与系统实际输出航向角ψ()k之间的误差来校正系统未来预测时域内的预测输出航向角ψ^( )k+i。误差表达式为

则校正后的系统未来预测时域内的无人船预测模型的输出航向角ψ^( )k+i表达式为
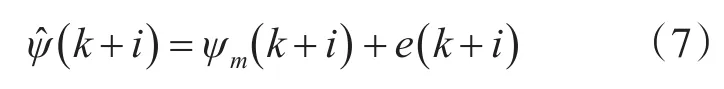
3.3滚动优化
基于预测函数控制的航向控制器通过滚动优化的方式来求解对应于每一个时刻的最优控制舵角输入量,该舵角控制量的求取标准是控制器对于预设航向的跟踪效果。另外,舵角控制量的选取在考虑航向最大化跟踪的同时,要考虑舵角的变化量符合无人船操舵的实际情况[7]。因此,构造如式(8)所示的标准函数J,对预测时域内航向跟踪误差的平方以及控制时域内舵角控制量变化增量的平方求加权平均值,并以标准函数J的最小化来获得无人船最优舵角输入控制量。通过调整标准函数中的加权因子来反应航向误差以及舵角增量在求解控制时域内最优舵角控制量时的重要程度。通常情况下,在满足无人船舵角约束的条件下,更注重航向控制效果,因此在式(8)中,航向误差加权因子ai要设置的比舵角控制量误差加权因子bi大。

其中,ψ是航向控制器的实际输出航向角,ψr是无人船的参考航向角,Hp是预测函数控制的预测时域,Hc是预测函数控制的控制时域,且满足Hc≤Hp,ai是航向误差加权因子,bi是舵角控制增量加权因子。
另外,根据无人船本身的控制特点,模型预测航向控制器在输出无人船的舵角控制量的过程中要考虑舵角约束。本文中使用的无人船模型舵角约束为
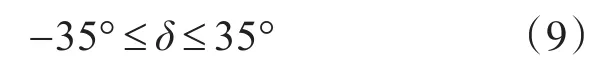
则滚动优化中求取k时刻最优舵角控制量问题可转化为如式(10)表示的局部最优控制问题,将k时刻式(10)求得的最优控制序列的第一个控制值作为k时刻最优舵角控制量作用于无人船航向控制系统,实现无人船的航向控制[8]。
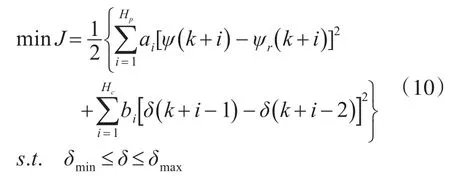
4 仿真验证及分析
本节以表1中介绍的无人船为基础,在Matlab仿真环境中对所设计的航向控制系统进行系统仿真,以验证控制器的可行性。系统仿真主要涉及航向保持和航向跟踪两个方面。具体参数设置如下:
1)无人船初始参数设置为:航速v=1m/s,航向角ψ=0°。
2)PID航向控制器参数设置:Kp=0.5,Ki=0.00005,Kd=0.9 。
3)PFC航向控制器参数设置:预测时域Hp=10;控制时域Hc=2。目标函数J中的航向误差加权因子 ai=1,i=1,2,…Hp,舵角控制增量加权因子 bi=0.1,i=1,2,…Hc[9]。
4.1 航向保持效果
在无干扰的理想情况下,对两种无人船航向控制器进行航向保持效果仿真。给定目标航向角ψd=10°的常值输入,获得的航向控制效果如图5所示,舵角控制量变化情况如图6所示。
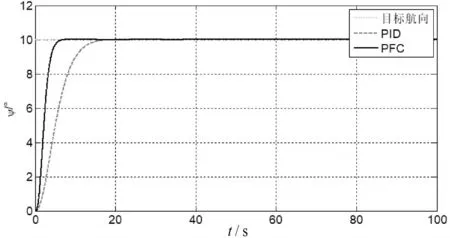
图5 航向保持效果图(无干扰)
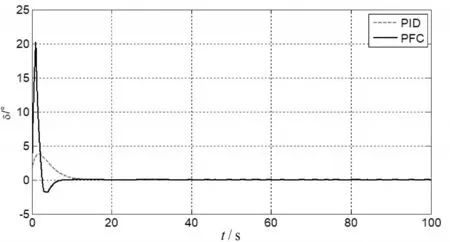
图6 航向保持舵角控制量(无干扰)
由图5和图6的仿真结果可以看出,在无干扰的理想情况下,基于PFC的航向控制器和基于PID的航向控制器都可以无超调的达到给定的目标航向角,基于PFC的航向控制器响应速度比基于PID的航向控制器要快,但是其舵角控制变化量较大。
在进行存在外部干扰的航向控制仿真中,风浪干扰项用一个白噪声乘以二阶波浪函数来代替[10],干扰信号中白噪声信号的均值为2,功率谱密度为0.5;二阶波浪函数表达式如式(11)所示,参数取值如下:增益常数 Kω=0.42,主导海浪频率ω0=0.606,阻尼系数ζ=0.3。

仿真实验中的干扰信号如图7所示。存在外部干扰情况下,两种航向控制器的控制效果如图8所示,对应的舵角控制量变化情况如图9所示。
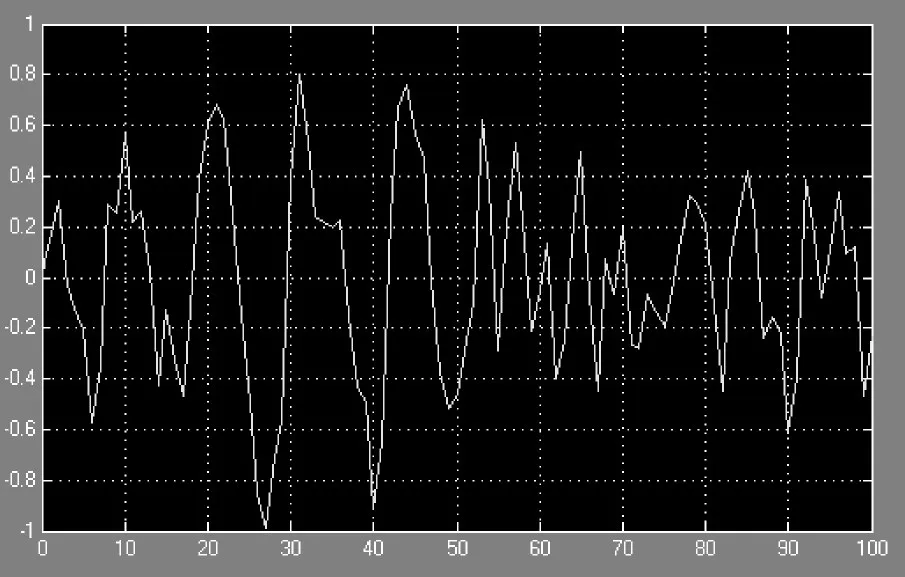
图7 风浪干扰信号
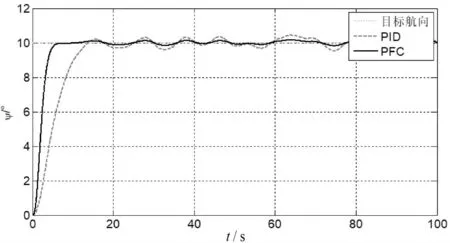
图8 航向保持效果(存在干扰)
根据图8和图9所示的仿真结果可以看出,当无人船航向控制系统存在外界风浪干扰时,预测函数控制的控制效果要优于经典PID控制。由图8的航向跟踪曲线可以看出,基于预测函数控制的航向控制系统能够更快地跟踪到目标航向,且在跟踪目标航向时的航向抖动更小[11~12]。由图9的舵角控制量变化曲线可以看出,基于预测函数控制的航向控制器的输出舵角控制量变化更加平滑。
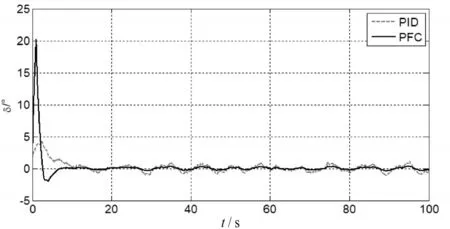
图9 航向保持舵角控制量(存在干扰)
4.2 航向跟踪效果
在无干扰的理想情况下,对两种航向控制系统的航向跟踪效果进行仿真。航向跟踪仿真实验给定无人船的目标航向角为幅值为90°、频率为0.02rad/s的正弦信号。仿真实验获得的两种控制器的航向跟踪效果如图10所示,舵角控制量变化曲线如图11所示。

图10 航向跟踪效果(无干扰)
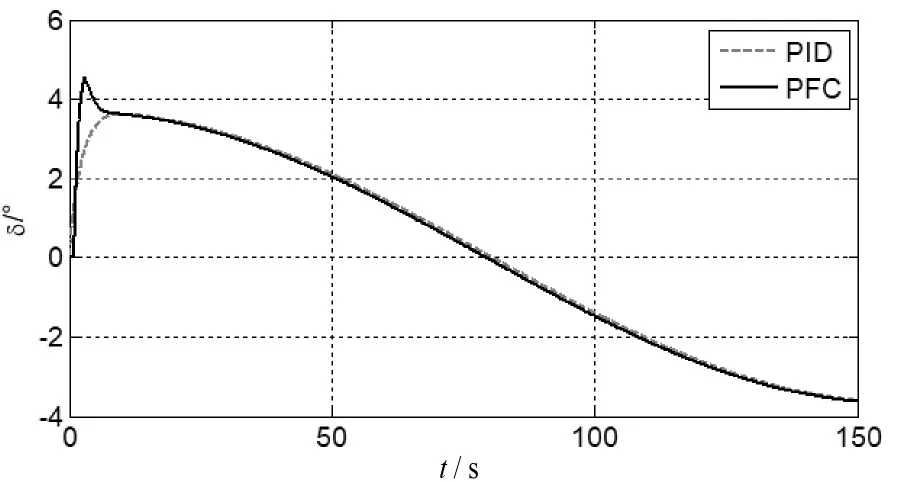
图11 航向跟踪舵角控制量(无干扰)
为了进一步分析基于PID的航向控制器和基于PFC的航向控制器的控制效果,表2给出了两种控制器的航向平均跟踪误差。从图10、图11以及表2可以看出,基于PFC的航向控制器能够实现稳定的航向跟踪性能,且跟踪速度和跟踪精度都高于传统的PID航向控制器。
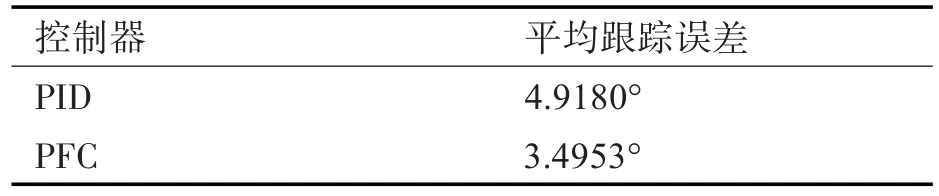
表2 航向跟踪误差
在存在外部干扰的情况下,给定无人船的目标航向角输入为幅值为90°,频率为0.02rad/s的正弦信号,进行两种航向控制器的航向跟踪效果仿真。干扰信号仍然采用式(11)所述的风浪干扰,干扰信号如图7所示。获得的航向跟踪效果如图12所示,舵角控制量变化如图13所示。
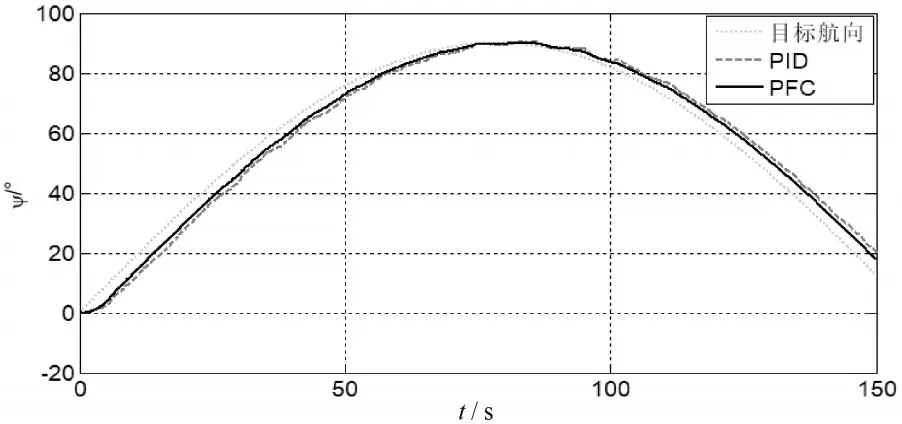
图12 航向跟踪效果(存在干扰)
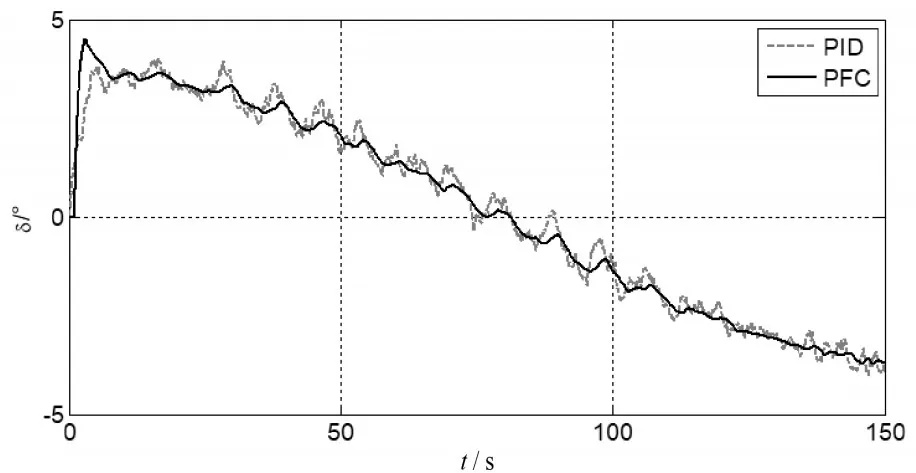
图13 航向跟踪舵角控制量(存在干扰)
为了进一步分析基于PID的航向控制器和基于PFC的航向控制器的控制效果,表3给出了两种控制器的航向跟踪误差。从图12、图13以及表3可以看出,基于PFC的航向控制器在有干扰的情况下也能够实现稳定的航向跟踪性能,且跟踪速度和跟踪精度都高于传统的PID航向控制器。

表3 航向跟踪误差(有干扰)
5 结语
基于预测函数控制的算法原理,与无人船航向控制的要求相结合,提出了一种基于预测函数控制的水面无人船航向控制器。通过将该航向控制器与基于经典PID算法的水面无人船航向控制器进行航向保持和航向跟踪的对比仿真实验,验证了基于预测函数控制的航向控制器有更好的航向保持和航向跟踪效果。
