基于SparkR的水文传感器数据的异常检测方法

刘子豪 李凌 叶枫

摘 要：为了高效地从海量的水文传感器数据中检测出异常值，提出一种基于SparkR的水文时间序列异常检测方法。首先，对数据进行清洗后，采用滑动窗口配合自回归积分滑动平均模型（ARIMA）在SparkR平台上进行预测;然后，对预测的结果计算置信区间，将在区间范围以外的判定为异常值;最后，基于检测结果，利用K均值算法对原数据进行聚类，同时计算其状态转移概率，对检测出的异常值进行质量评估。以在滁河获取的水文传感器数据为实验数据，分别在运行时间和异常值检测效果这两个方面进行了实验。结果显示：利用SparkR对百万级数据进行计算时，利用双节点计算的时间要长于单节点;但是对千万级数据进行计算时，双节点比单节点计算时间上更少，最多减少了16.21%，且评估过后的灵敏度由之前的5.24%提高到了92.98%。实验结果表明，在SparkR下，根据水文数据的特点并结合预测检验和聚类校验的方法对千万级水文时间序列进行检测时，能有效提高传统方法的计算效率，并且在灵敏度方面相比传统方法也有显著提升。

关键词：SparkR;自回归积分滑动平均模型;异常检测;水文时间序列;K均值

中图分类号： TP391

文献标志码：A

Abstract： To efficiently detect outliers in massive hydrologic sensor data， an anomaly detection method for hydrological time series based on SparkR was proposed. Firstly， a sliding window and Autoregressive Integrated Moving Average （ARIMA） model were used to forecast the cleaned data on SparkR platform. Then， the confidence interval was calculated for the prediction results， and the results outside the interval range were judged as anomaly data. Finally， based on the detection results， K-Means algorithm was used to cluster the original data， the state transition probability was calculated， and the anomaly data were evaluated in quality. Taking the data of hydrologic sensor obtained from the Chu River as experimental data， experiments on the detection time and outlier detection performance were carried out respectively. The results show that the millions of data calculation by two slaves costs more time than that by one slave， but when calculating the tens of milllions of data， the time costed by two slaves is less than that by one slave， and the maximum reduction is 16.21%. The sensitivity of the evaluation is increased from 5.24% to 92.98%. It shows that under big data platform， the proposed algorithm which is based on the characteristics of hydrological data and combines forecast test and cluster test can effectively improve the computational efficiency of hydrologic time series detection for tens of millions data and has a significant improvement in sensitivity.

Key words： SparkR; AutoRegressive Integrated Moving Average （ARIMA） model; anomaly detection; hydrologic time series; K-Means

0 引言

水文數据是按其物理量分为各种类型的水文时间序列。目前许多专家认为，水文时间序列一般由确定分量和随机分量组成。确定分量具有一定的物理概念，随机分量则由不规则的震荡和随机影响产生[1]。水文时间序列主要表现出随机性、模糊性、非线性、非平稳性和多时间尺度变化等复杂特性[2]。随着物联网、传感器技术的迅猛发展，水利信息化部门越来越多地采用传感器技术来获取水文数据，这里面往往也包含许多异常值。对于水文时间序列来说，与一般规律相差较大的数值， 便可以将其判定为异常数据[3]。异常值往往包含着重要的信息，通过精确找到隐藏在数据背后的隐藏值，对之后的分析决策意义重大。目前，对于水文时间序列，传统的方法只适用于小数据集，不适用于现在的大数据环境，且精度仅在特异度方面达到了99%[4]的水准，灵敏度仍有提升空间。以滑动窗口算法为例，虽然理论上它可以作用于任意长度的数据集，但是对于海量数据，它的计算复杂度较高且灵敏度低。

本文提出了一种基于SparkR的海量水文时间序列异常检测方法，将预测检验和聚类检测进行结合。首先，对得到数据进行清洗、降维、去重、筛选和排序;之后，采用滑动窗口配合自回归积分滑动平均模型（AutoRegressive Integrated Moving Average， ARIMA）进行预测，并对预测的结果计算置信区间，在区间范围以外的，将其判定为异常值。针对海量水文数据的特点，在检测完成后利用K均值（K-Means）对原数据进行聚类，同时计算其状态转移概率，对检测出的异常值进行质量评估，提高灵敏度。该方法可以在海量水文时间序列中有效提高滑动窗口法的计算效率，同时还给出了可靠的置信度来提升整体的灵敏度，能快速准确地在海量水文时间序列中检测出异常值。相比传统的滑动窗口检测算法，本文利用大数据处理平台SparkR提高了算法的计算效率;同时还提出了一种结合预测检验和聚类校验的异常检测方法，通过对传统的滑动窗口算法进行校验，保留了滑动窗口算法特异度高的优势，并解决了该算法灵敏度过低的问题。

1 相关工作

1.1 异常检测

异常值[5]是在数据集中偏离大部分数据的数据，这些数据疑似并非为随机误差所致，而是产生于完全不同的机制。对于异常检测，一些有代表性的方法包括：牛丽肖等[6]提出的一种基于小波变换和ARIMA的短期电价混合预测模型， 该模型确实可以检测到突变点的情况，但对非线性的部分或者时间序列过长的数据则存在着不足。任勋益等[7]提出了一种基于向量机和主元分析的异常检测，先用主元分析法降低维度，再用支持向量机（Support Vector Machine， SVM）建模并检验异常数据;但当数据中存在较多种类异常值时，该方法的检测精确度不高且计算复杂度高。孙建树等[3]提出了基于ARIMA-SVM的水文时间序列异常值检测，该方法使用ARIMA预测线性部分，使用SVM预测非线性部分，将两部分的值相加得到最终预测的结果并将不在置信区间的值判定为异常值。这类算法在处理小规模数据集时效果较好，但是无法处理多元和大规模的数据，而且阈值的确定也较为困难。

基于距离检测的方法是设定某种距离函数对数据点进行距离计算，当一个点与其余点距离过大时，将其视为异常点。Vy等[8]提出了针对时间序列可变长度的异常检测算法：先对时间序列分段;然后对每种模式的异常因子进行计算，计算出异常因子之间的距离;最后根据该异常因子距离判断是否为异常。该方法的优点是便于用户使用，时间复杂度相对较小，不足在于对局部异常点不敏感。

Breunig等[9]提出了局部异常因子（Local Outlier Factor，LOF）的概念来计算数据集密度。LOF越大，意味着对象离群程度越高，是异常值可能性就越高;但是不同密度的子集混合会造成检测错误，虽然后续又有人提出了相关改进方案，但是总体时间复杂度较高。

1.2 SparkR

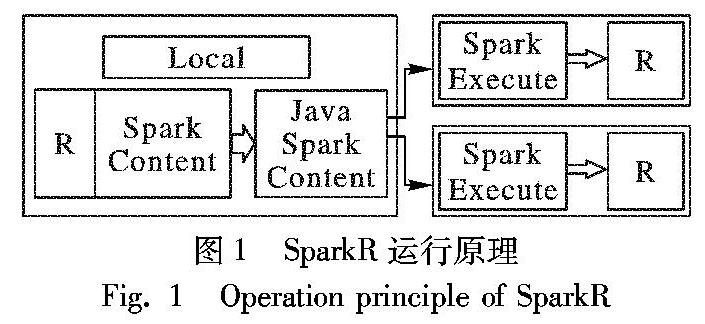
SparkR[14]是一个提供轻量级前端用于在R中使用Apache Spark的R包，它提供了分布式数据框架接口，可以支持选择、过滤、聚集等操作。到Spark2.3.0，SparkR可以用来操作数据框，而且可以通过MLlib使用分布式的机器学习。弹性分布式数据集（Resilient Distributed Dataset， RDD）是Spark的基础数据模型[15]，是容错、并行、只读的数据结构，它允许用户存储数据在磁盘和内存中，并且控制数据分区;同时，它也是一个分布式的内存抽象，代表一个只读部分记录的集合，并且只能被存储在稳定的物理存储或者其他现有的RDD中;它只能通过对数据集执行某些确定性的操作来创建;而且它只支持粗粒度转换，也就是说在许多记录上执行单个操作。DataFrame是Spark推出的应用程序编程接口（Application Programming Interface， API），主要应用于大数据处理方面，基于DataFrame，所有主要的数据源会被连接并自动转换为并行处理形式。DataFrame是Spark SQL、Streaming和MLlib的基础。SparkR支持常见的闭包功能，用户定义函数中引用的变量会自动发送到群集中的其他计算机。SparkR的运行原理如图1所示。

2 关键实现

2.1 算法描述

本文基于SparkR的水文时间序列异常检测算法结合了预测检验和聚类检测两个过程。首先，采用预测检验的思想对时间序列{x1，x2，…，xn}建立ARIMA模型，采用滑动窗口的方式得到预测出的置信区间，并与原数据进行对比，识别出异常值;在检测出异常值之后，采用K-Means算法对原始的数据进行聚类，聚类出结果之后计算出其状态转移矩阵，用状态转移矩阵对之前得到的异常值进行异常评估，最后确定异常值。

2.2 基于滑动窗口的异常值检测

定义水文时间序列X中待检测点Xi的滑动邻居窗口Li，为了降低算法复杂性，采用该点的前L个点作为预测模型输入参数进行计算。本算法选择预测节点的左鄰居窗口作为算法输入，单边定义如下：

基于滑动窗口的异常检测，核心是建立ARIMA模型[16]，通过滑动窗口的输入来预测观测点的值，得到一系列预测值。首先要对时间序列进行单位根检验，如果是非平稳序列，就要通过差分来转化为平稳序列。以AIC（Akaike Information Criterion）为准，需要确定自回归阶数p和移动平均阶数q，找出具有最小ACI值的p、q组合。ARIMA模型是针对非平稳时间序列建模，适用于水文时间序列。本文取置信区间为95%。将ARIMA模型计算出的置信区间与原始序列进行比较，不在置信区间内的即判定为异常值。

2.3 基于K-Means模型的异常值校验

2.3.1 状态转移概率矩阵

通过滑动窗口配合ARIMA识别出异常值之后，还要计算出异常点的置信度，用来判定该点是否确实为异常点，以减少误判，降低人工工作量。

K-Means算法属于聚类算法中的一种，其原理是：给定K（K代表要将数据分成的类别数）的值，然后根据数据间的相似度将数据分成K个类，也称为K个簇（cluster）。度量数据相似度的方法一般是用数据点间的距离来衡量，比如欧氏距离、汉明距离、曼哈顿距离等。一般来说，可使用欧氏距离来度量数据间的相似性。比如，对于二维平面上的两个点A（x1，y2）和B（x2，y2），两者间的欧氏距离为：（x1-x2）2+（y1-y2）2。

而对于每一个簇，用簇中所有点的中心来描述，该中心也称为质心（centroid）。通过对簇中的所有数据点取均值（mean）的方法来计算质心。具体来说，K-Means将整个时间序列{x1，x2，…}作为输入，序列T={T1，T2，…}作为输出，将时间序列上的点转换为各个聚类点，{T1，T2，…}表示这一时间点上属于哪一个中心，对时间序列进行了状态分类。之后用前面获得的异常值和其前一时刻值当作输入，提供给K-means模型后，计算每个样本与聚类中心的距离，即计算样本与状态向量的相似度，然后把聚类中心分配给每一个样本。

K-Means模型训练结束后，可以得到状态序列T，通过计算可以得到一个状态转移矩阵，为了便于之后的计算，将矩阵转换为数据框。该数据框有三列，第一列代表状态i，第二列代表状态j，第三列表示状态i转移到j的概率。假设某时间序列{xi，xi+1}通过 K-Means模型转换得到对应的状态序列为prob，Xi+1出现在Xi之后，换言之相当于发生了一次从状态Ti到Tj的转移，转移概率为：

pij=状态Ti转移到状态Tj的次数状态Ti转移到所有其他状态的次数

2.3.2 异常值校验

本文采用发生转移的概率与由前一时刻的状态转移到下一个最有可能的状态的概率相比，作为评价标准。假设Xi为待检验异常点，前一时刻的值为Xi-1，转换后得到的状态为Ti和Ti-1，Ti-1最有可能转移到的状态记为Tm，由此定义一个异常值概率：

pi=1-状态Ti-1转移到状态Ti的概率状态Ti-1转移到Tm的概率由上式可知，状态Ti-1转移到Tm的概率为定值，状态Ti-1转移到状态Ti的概率越小，pi越大，则Xi为异常值的概率越大。

由于现实中水文数据的异常判定往往以变化量大于2cm作为异常值的判定，利用K-Means作聚类可能会出现异常值和其前一时刻的值处于同一状态下而导致漏判的情况，故在判定异常值后需要将异常值概率为0但是相差大于2cm的值也判定为异常值。

2.3.3 SparkR

本次实验基于Spark RDD/DataFrame 形成数据模型，并将所有的数据通过相应的数据源输入并转换成RDD/DataFrame 模式。应用gapply函数可以实现在SparkR上运行R程序。

3 实验与讨论

3.1 实验环境和配置

本次仿真使用双节点：一台PC为8核，8GB内存;另一台PC为16核，8GB内存。相关软件版本如下：Java 1.8，Spark 2.3，Hadoop 2.7，R 3.4.4和SparkR 2.3。实验数据来自江苏省各个水文站从2016年到2017年的数据，共18910864条数据。

3.2 实验结果与分析

3.2.1 数据清洗

在进行异常检测之前，需要对取得的数据进行数据清洗，清洗前部分数据如表1所示。从表1可以看到，原始数据存在诸多问题，如重复、排序混乱、时刻格式不符合数据挖掘要求、存在无关数列等。针对以上问题，本文基于SparkR对初始的18910864條水文数据进行了清洗，并比较了计算资源和数据量的关系，结果如表2所示。

如表2所示，当选取15个站点时，双节点的运行速度慢于单个节点，但随着数据量的增加，用双节点计算的结果变化浮动较小，而只用单节点时间有着明显上升。SparkR在数据清洗后的部分数据如表3所示。可以看到，数据按照水文站编号进行了分组并按时间顺序排列，同时删除了跟结果无关的记录格式列，降低了计算量。经清洗后，数据只剩下水文站编号、时间以及水位值，符合数据挖掘要求。

3.2.2 检测时间

本节实验主要针对基于滑动窗口进行时间序列预测时计算复杂度高、运行计算时间过长的问题，采用SparkR进行计算，比较不同的计算资源下利用SparkR执行该算法的时间，结果如表4所示。可以看到，在选择的15个和35个水文站点数据下，双节点运行速度并不理想，但当数据量上升到千万级別时，双节点的优势就可以体现出来，时间增长速度以及计算时间都占据优势。可见，在更大的数据集下，双节点下运行速度更快，最快情况下检测时间减少了16.21%。

3.2.5 有效性与准确性

为了验证本文算法的有效性和准确性，本文将实验结果分为4类：第一类为TP（True Positive），表示实际为异常被判定为异常;第二类为FN（False Negative），表示实际为异常被判定为正常;第三类为FP（False Positive），表示实际为正常被判定为异常;第四类为TN（True Negative），表示实际为正常被判定为正常。TP和TN是最理想的情况，FN和FP是不希望出现的情况。本文定义了算法的灵敏度Sensitive=TP/（TP+FP）和特异度Specificity=TN/（TN+FN）作为评价指标。

本文采用的数据集为编号12910280水文站2016—2017年的数据，共计155464条，将传统滑动窗口算法和本文算法用于同一水文时间序列进行了对比，结果如表7所示。由表7可以看到，改进后的模型保留了滑动窗口检测的优势，在FN和TP方面保持不变，保留了传统方法在特异度方面的优势，但在FP方面，因为先前给予滑动窗口预测的方法在判断异常值方面界限比较模糊，对于日均水文数据，由于数值间相差较大，所以灵敏度即正确率比较高，但是对于每隔5min接收一次的水文传感器数据来说，水位变化较小，误检率就会变高，因此在检测完之后添加了异常值评估，这样可以显著减少错判，提升正确率。

經计算，在特异度方面二者相差无几，改进前为99.95%，改进后为99.97%，但灵敏度由改进前的5.24%提高到了92.15%，得到了显著的提高。这表明本文算法在传统算法的基础上引入SparkR后解决了传统滑动窗口算法计算复杂度高的问题，同时通过增加聚类校验能够有效地检测出水文时间序列中的异常值，且正确率也比较高。

4 结语

在大数据背景下，传统的检测算法已经不能够适应当今的需求。本文利用滑动窗口的特点，同时针对传统滑动窗口检验的缺陷，如时间复杂度高、误检率高等缺点，提出了一种基于SparkR的水文时间序列异常检测方法。该方法使用SparkR进行计算，减少了计算时间;而且结合了预测检验和聚类检测两个过程，利用ARIMA模型对时间序列的水文数据进行建模来预测可能的异常点，再利用K-means聚类后计算状态转移矩阵，根据水文数据的特点对异常点进行判定。结果表明：基于SparkR对百万级数据进行计算时，利用双节点计算的时间要长于单节点;但是对千万级数据进行计算时，双节点比单节点计算时间少，时间最多能减少1621%;且评估过后的灵敏度由之前的5.24%提高到了9298%。这表明本文算方法在对千万级水文数据进行检测时，利用SparkR通过增加节点的方式可以有效提高滑动窗口法的计算效率，而且在灵敏度方面相比传统滑动窗口检测方法也有显著提升。但是，本文算法在检测正确率上仍有进一步完善的空间，后续工作将聚焦于更加精确地辨识出哪些为异常值、哪些为由自然因素引起的正常波动。

参考文献：

[1] 吴德.水文时间序列相似模式挖掘的研究与应用[D].南京：河海大学，2007.（WU D. Research and application of hydrological time series similarity pattern[D]. Nanjing： Hohai University， 2007.）

[2] 桑燕芳，王中根，刘昌明.水文时间序列分析方法研究进展[J].地理科学进展，2013，32（1）：20-30. （SANG Y F， WANG Z G， LIU C M. Research progress on the time series analysis methods in hydrology[J]. Progress in Geography， 2013， 32（1）： 20-30.）

[3] 孙建树，娄渊胜，陈裕俊.基于ARIMA-SVR的水文时间序列异常值检测[J].计算机与数字工程，2018，46（2）：225-230. （SUN J S， LOU Y S， CHEN Y J. Outlier detection of hydrological time series based on ARIMA-SVR model[J]. Computer & Digital Engineering， 2018， 46（2）：225-230.）

[4] 余宇峰，朱跃龙，万定生，等.基于滑动窗口预测的水文时间序列异常检测[J].计算机应用，2014，34（8）：2217-2220，2226. （YU Y F， ZHU Y L， WAN D S， et al. Time series outlier detection based on sliding window prediction[J]. Journal of Computer Applications，2014，34（8）：2217-2220，2226.）

[5] HAWKINS D M. Identification of Outliers[M]. Berlin： Springer， 1980：27-41

[6] 牛丽肖，王正方，臧传治，等.一种基于小波变换和ARIMA的短期电价混合预测模型[J].计算机应用研究，2014，31（3）：688-691. （NIU L X， WANG Z F， ZANG C Z， et al. Hybrid model based on wavelet and ARIMA for short-term electricity price forecasting[J]. Application Research of Computers，2014，31（3）：688-691.）

[7] 任勋益，王汝传，孔强.基于主元分析和支持向量机的异常检测[J].计算机应用研究，2009，26（7）：2719-2721. （REN X Y， WANG R C， KONG Q. Principal component analysis and support vector machine based anomaly detection[J]. Application Research of Computers，2009，26（7）：2719-2721.）

[8] VY N D K， ANH D T. Detecting variable length anomaly patterns in time series data[C]// Proceedings of the 2016 International Conference on Data Mining and Big Data， LNCS 9714. Berlin：Springer， 2016： 279-287.

[9] BREUNIG M M， KRIEGEL H-P， NG R T， et al. LOF： Identifying density-based local outliers[C]// Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2000：93-104.

[10] 潘渊洋，李光辉，徐勇军.基于DBSCAN的环境传感器网络异常数据检测方法[J].计算机应用与软件，2012，29（11）：69-72. （PAN Y Y， LI G H， XU Y J. Abnormal data detection method for environment wireless sensor networks based on DBSCAN[J]. Computer Applications and Software， 2012， 29（11）： 69-72.）

[11] twitter/AnomalyDEtection [EB/OL]. [2015-09-01]. https：//github.com/twitter/AnomalyDetection.

[12] 杨志勇，朱跃龙，万定生.基于知识粒度的时间序列异常检测研究[J].计算机技术与发展，2016，26（7）：51-54. （YANG Z Y， ZHU Y L， WAN D S. Research on time series anomaly detection based on knowledge granularity[J]. Computer Technology and Development， 2016， 26（7）：51-54.）

[13] 刘雪梅，王亚茹.基于异常因子的时间序列异常模式检测[J].计算机技术与发展，2018，28（3）：93-96. （LIU X M， WANG Y R. Anomaly pattern detection in time series based on outlier factor[J]. Computer Technology and Development， 2018， 28（3）：93-96.）

[14] Spark R （R frontend for Spark） [EB/OL]. [2016-06-11]. https：//github.com/amplab-extras/SparkR.pkg.

[15] 譚旭杰，邓长寿，董小刚，等.SparkDE：一种基于RDD云计算模型的并行差分进化算法[J].计算机科学，2016，43（9）：116-119，139. （TAN X J， DENG C S， DONG X G， et al. SparkDE： a parallel version of differential evolution based on resilient distributed datasets model in cloud computing[J]. Computer Science， 2016， 43（9）：116-119，139.）

[16] CONTRERAS J， ESPINOLA R， NOGALES F J， et al. ARIMA models to predict next-day electricity prices[J]. IEEE Transactions on Power Systems，2003，18（3）：1014-1020.