基于最优最小生成树的三维模型形状优化方法
2019-07-31韩丽刘书宁于冰徐圣斯唐棣
韩丽 刘书宁 于冰 徐圣斯 唐棣


摘 要:针对海量、异构、复杂的三维模型高效形状分析需求,提出基于最优最小生成树的三维模型形状优化方法。首先基于三维模型的初始最小生成树(3D-MST)构造模型的结构描述;其次通过拓扑结构与几何形状检测并结合双边滤波与熵权值分布进行局部优化,获得模型的优化MST表示;最终基于优化的Laplacian谱特征,结合薄板样条函数(TPS),实现模型的形状分析与相似性检测。实验结果表明,所提方法不仅有效地保留了模型的形状特征,而且可高效地实现复杂模型的稀疏优化表示,能进一步提高几何处理与形状检索的高效性和增强鲁棒性。
关键词:最小生成树; 体积; 双边滤波; 熵权值; 谱嵌入
中图分类号: TP391.41
文献标志码:A
文章编号:1001-9081(2019)03-0858-06
Abstract: For the efficient shape analysis of massive, heterogeneous and complex 3D models, an optimization method for 3D model shape based on optimal minimum spanning tree was proposed. Firstly, a model description based on 3D model Minimum Spanning Tree (3D-MST) was constructed. Secondly, local optimization was realized by topology and geometry detection and combination of bilateral filtering and entropy weight distribution, obtaining optimized MST representation of the model. Finally, the shape analysis and similarity detection of the model were realized by optimized Laplacian spectral characteristics and Thin Plate Spline (TPS). The experimental results show that the proposed method not only effectively preserves shape features of the model, but also effectively realizes sparse optimization representation of the complex model, improving the efficiency and robustness of geometric processing and shape retrieval.
Key words: Minimum Spanning Tree (MST); volume; bilateral filtering; entropy weight; spectral embedding
0 引言
随着三维扫描、三维重建技术的发展,三维模型已经广泛应用于建筑、医疗、教育、影视娱乐等各行各业,尤其随着互联网及大数据技术的发展,三维模型的数据量与复杂度更是显著提高,基于三维模型优化的形状分析方法更显得尤为重要。
三维模型形状分析的关键在于特征描述符的选择,通过对比特征描述符获得模型的相似性。目前常用的三维模型形状特征描述符有基于几何特征统计直方图的方法、基于骨架拓扑结构的方法、基于视觉相似投影的方法以及基于谱分析的方法。其中,基于几何特征统计直方图的方法是通过计算模型顶点和网格的几何信息分布特征来分析三维模型,如Osada等[1]提出了一种形状分布(Shape Distribution, SD)直方图算法,选择恰当的形状函数度量模型,如通过计算顶点间的欧氏距离获得模型的形状分布直方图; Pickup等[2]提出基于模型表面积的分布直方图(Surface Area, SA)。该类方法能有效描述模型的全局特征,但是忽略了模型的局部特征。李海生等[3]针对局部细节特征提出一种基于模型内二面角的分布直方图的特征描述方法,但该方法在噪声干扰、网格简化时,鲁棒性较差。基于骨架拓扑结构的方法是通过简化算法获取模型的拓扑结构,有效去除模型的冗余信息,提供更直观、简洁的形状描述,被广泛应用于模型的形状匹配与检索,如Reeb图[4]、中轴线法[5]。这类方法虽然对扰动噪声具有鲁棒性,能够表现出模型的整体特征,但是缺乏对细节的描述,并且计算量大。为此,王飞等[6]针对局部细节特征的不足,提出一种拓扑与形状特征相结合的三维模型描述方法。该方法虽然能较好地提取模型的局部特征形状,但是对于高精度的模型还需深入研究。 基于视觉相似方法是通过比较多视角下三维模型的二维图像进行匹配。如文献[7]利用马尔可夫链(Markov Chain, MC)模擬同一物体多视角的统计特性来进行模型的相似性分析;文献[8]提出一种多视角与图方法结合的多视角权重匹配方法,具有较好的效果,但是该类方法不具有旋转、缩放的特性,且计算量大。
近年来,谱分析的方法广泛应用于三维模型的检索与匹配[9-12]。基于谱分析的方法是利用拉普拉斯算子将三维模型映射到谱特征空间,不仅能较好地保持模型的内蕴属性,具有等距不变性,并且能够有效提高非刚性模型的匹配精度。例如,Lipman等[9]基于谱方法实现全局内蕴的检测;Sahillioglu等[10]在谱域构造初始化匹配,采用贪婪算法结合等距性优化匹配结果;Sun等[11]基于模型表面热扩散提出热核特征(Heat Kernel Signature, HKS);Aubry等[12]将波动方程引入模型,提出波核特征(Wave Kernel Signature, WKS)的形状分析方法。谱特征由于具有较强的稳定性与抗噪性,被进一步应用于模型对称性检测、形状配准、深度学习中。文献[13]使用选举和谱分析方法提出一种模型局部内蕴对称检测算法;文献[14]基于热核分布识别精度不突出问题,提出热模态特征,提高了模型的检索精度。
然而,针对既能突出模型的局部细节,又能反映模型的整体特征的高效分析算法仍需进一步研究。本文提出一种兼顾模型全局结构与局部几何细节的模型形状分析与匹配算法,通过拓扑结构与几何形状检测,并结合图像中双边滤波的思想与熵权值分布实现三维模型最小生成树(Three-dimensional model Minimum Spanning Tree, 3D-MST)的优化,构造模型的稀疏表示;进而获得优化的3D-MST谱特征;最终基于薄板样条函数(Thin Plate Spline, TPS),实现模型的形状分析与相似性检测,本文方法有效提高了模型优化表示与形状分析效率。
1 相关理论
1.1 三维模型最小生成树
最小生成树(Minimum Spanning Tree, MST)是一个优化的数学模型,可有效描述模型的拓扑结构,被广泛用于网络设计[15]和数据挖掘[16]等领域。其经典算法有Prim算法和Kruskal算法。Prim以任意顶点出发,逐次加入生成树点集中最近的模型顶点,适用于边稠密的最小生成树。而Kruskal算法算法适用于边稀疏的最小生成树。为了有效保持复杂模型的形状结构,本文采用Prim算法构建初始的三维最小生成树(3D-MST)。
图1为虎的原始网格模型、三维模型最小生成树以及基于本文算法优化后的三维模型最小生成树。
1.2 几何形状特征
稳定有效的形状特征描述是形状分析的至关重要因素。最常用的形状描述符有高斯曲率(Gaussian Curvature, GC)[17]、可视化体积[18] 、形状直径(Shape Diameter Function, SDF)[19]、平均测地线距离(Average Geodesic Distance, AGD)[20]、形状分布(SD)[1]等。
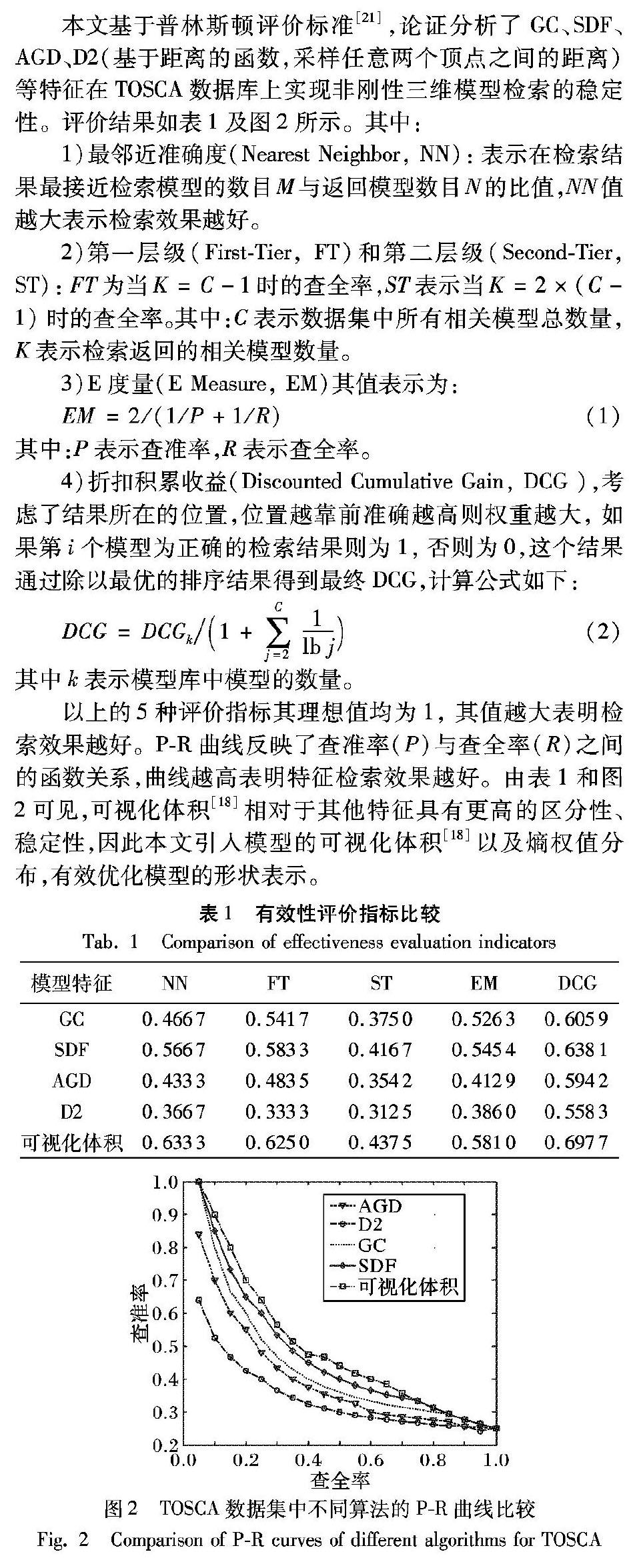
本文基于普林斯顿评价标准[21],论证分析了GC、SDF、AGD、D2(基于距离的函数,采样任意两个顶点之间的距离)等特征在TOSCA数据库上实现非刚性三维模型检索的稳定性。评价结果如表1及图2所示。其中:
1)最邻近准确度(Nearest Neighbor, NN):表示在检索结果最接近检索模型的数目M与返回模型数目N的比值,NN值越大表示检索效果越好。
2)第一层级(First-Tier, FT)和第二层级(Second-Tier, ST):FT为当K=C-1时的查全率,ST表示当K=2×(C-1)时的查全率。其中:C表示数据集中所有相关模型总数量,K表示检索返回的相关模型数量。
3)E度量(E Measure, EM)其值表示为:
4)折扣积累收益(Discounted Cumulative Gain, DCG ),考虑了结果所在的位置,位置越靠前准确越高则权重越大,如果第i个模型为正确的检索结果则为1,否则为0,这个结果通过除以最优的排序结果得到最终DCG,计算公式如下:
其中k表示模型库中模型的数量。
以上的5种评价指标其理想值均为1, 其值越大表明检索效果越好。P-R曲线反映了查准率(P)与查全率(R)之间的函数关系,曲线越高表明特征检索效果越好。由表1和图2可见,可视化体积[18]相对于其他特征具有更高的区分性、稳定性,因此本文引入模型的可视化体积[18]以及熵权值分布,有效优化模型的形状表示。
2 三维模型MST优化表示
为获取稳定的形状检测,减少噪声的影响,本文从局部双边滤波到整体信息熵优化,高效实现模型的最优表示。
2.1 基于双边滤波的局部优化
双边滤波是一种非线性滤波的方法,广泛应用于图像处理中[22],可以达到保边去噪的效果。滤波器由两个测量函数构成:一个几何空间的距离测量,决定滤波系数d;另一个是像素灰度的特征测量,决定滤波系数r。像素的输出值依赖于邻域的像素值的加权组合。
本文基于图像双边滤波思想与信息熵理论,通过测地线距离度量几何空间差异,采用体积特征度量模型的特征差异,与三维模型MST相结合构造模型的优化表示。
距离滤波系数为:
图3为victoria模型滤波前后的局部顶点的体积特征对比折线图,可见滤波后的体积特征,不仅保持模型的整体形状特征,而且有效实现模型的平滑过渡。
2.2 基于信息熵的全局优化
熵本身是热力学概念,用来表达分子状态杂乱程度的一个物理量。美国信息论创始人香农引入信息熵用来表示信息量,信息熵越大表示信息量越小,反之信息量越大。近年来信息熵被广泛引用于图形图像的检索与特征选择[23]。但信息熵强调整體模型的特征分布,忽略了模型的局部信息。本文引入局部滤波的形状特征,结合信息熵分布,实现全局的模型优化表示。
若d≤γ,则保留父节点,删除其子节点;若d>γ,则两节点均保留。
图4分别表示victoria模型的最小生成树、模型的特征点分布以及最优最小生成树。模型的特征点不但降低了模型的密度,而且可以提高模型的检索效率。
图5为本文方法在不同模型上的优化结果, 从左到右依次为优化30%、50%、70%的MST。
图7为不同模型在不同优化率下的熵权分布情况。由折线图可以看出,对于同类模型虽然优化率不同,但模型的熵权概率分布相似(如站和抬腿),表明了体积的熵权值,具有稳定的形状描述能力,能够在不同优化率下很好地保留模型的形状特征,对噪声具有较强的鲁棒性,能够有效地识别不同种类模型(如人体模型与狼模型)。
3 基于谱图的形状匹配
3.1 模型特征点的谱嵌入
拉普拉斯映射的谱嵌入将高维数据嵌入到低维空间,可以有效保持模型的内蕴特征。本文基于最优最小生成树建立拉普拉斯矩阵,计算模型的谱特征 [24-25],并结合TPS配准方法,实现模型的形状配准与分析。
如图8表示,其中第一列为初始模型,第二列为模型的拉普拉斯谱域,第三列为实现MST优化后的稀疏谱图。所示,稀疏表示的谱图有效保持原有模型的整体结构特征。
综上所述,完整的最优最小生成树的模型相似性度量算法步骤如下:
输入: 待匹配的模型X,Y;
输出: 模型的谱域配准率sim(X,Y)。
步骤1 提取模型的初始MST;
步骤2 提取模型的内部可视化体积并使用双边滤波进行优化;
步骤3 计算模型的熵权值;
步骤4 利用熵权分布及初始MST获取模型特征点;
步骤5 获取特征点的最优MST并提取其谱域;
步骤6 利用TPS获取模型的配准率sim(X,Y)。
如图9表示不同模型间的配准结果。
4 实验结果与分析
本文实验在TOSCA三角网格数据库(简称TOSCA数据库)上进行测试,所有实验都在平台为Pentium 3.2GHz CPU, 8GB内存Windows7操作系统的PC上完成的,并使用VC++6.0和OpenGL2.0图形库作为可视化开发环境。
本文算法主要由四阶段组成,1)原始模型最小生成树的生成;2)基于双边滤波的局部特征优化;3)基于熵权值分布的整体3D-MST优化;4)基于谱图的模型匹配。
为了验证本文模型优化方法的稳定性,将本文方法与文献[25]方法和CPD[27]在TOSCA数据库进行实验对比。该数据中包含12个类,148个模型非刚性模型,尽管该数据库规模较小,但是选取的模型的不同姿势具有代表性。该模型数据库中的部分模型如图10所示。
图11(a)、(b)、(c)为本文方法、文献[25]方法与CPD方法的谱域配准实验结果,图11(d)为稀疏谱域配准点在空域中模型形状匹配结果显示。
图12表示基于三种不同方法,以猫模型为待检索样本,在数据库中获得的三维模型检索结果。
可见本文方法对于同类模型不仅配准率稳定,而且模型顶点优化率高、更为高效(如表2所示),对于不同类模型更能进行有效的区分。因此运用本文方法不仅实现模型的优化稀疏表示以及形状检测,更有效提高模型的检索效率。
如图13所示,不同优化率下,同类模型之间具有较高的匹配度。当优化率为80%以下时,稀疏后的模型能够保留稳定的形状信息,具有较高的模型识别度和匹配度,但是当优化率大于80%时,由于剩下的形状信息较少,配准率急速下降。因此,实验中为了有效保留形状信息,本文约束模型的优化率取为80%。
图14为相关方法的P-R曲线,可见,本文方法对于同类模型不仅配准稳定与精准,对于不同类模型更能进行有效的区分。
5 结语
针对三维模型的高效形状分析与检索需求,提出了一种三维模型最小生成树优化表示算法。通过内部可视化体积获取模型顶点的熵权分布,运用熵权值对模型MST自下而上进行三维模型的优化,最终得到三维模型的MST优化表示。
为了验证优化模型的形状稳定性,本文提取优化模型的谱特征,运用TPS方法,进行模型的配准与相似性分析,实验结果进一步验证了本文方法有效保持模型的形状特征,实现了复杂模型的稀疏优化表示,为进一步的模型几何处理以及检索等应用奠定了基础。本文方法使用了TPS非刚性配准算法,在大规模线性求解方面效率较低,容易产生不稳定的解,在建立点对点的对应关系时可能会出现配准误差。在接下来的工作中,将基于现有的研究与理论进一步提高模型的配准效率。
参考文献 (References)
[1] OSADA R, FUNKHOUSER T, CHAZELLE B, et al. Shape distributions [J]. ACM Transactions on Graphics, 2002, 21(4): 807-832.
[2] PICKUP D, SUN X, ROSIN P L, et al. Shape retrieval of non-rigid 3D human models [C] // 3DOR '14: Proceedings of the 7th Eurographics Workshop on 3D Object Retrieval. Aire-la-Ville, Switzerland: Eurographics Association, 2014: 101-110.
[3] 李海生,孫莉,吴晓群,等.基于模型内二面角分布直方图的非刚性三维模型检索[J].计算机辅助设计与图形学学报,2017,29(6):1128-1134.(LI H S, SUN L, WU X Q, et al. Non-rigid 3D shape retrieval based on inner dihedral angle histogram [J]. Journal of Computer-Aided Design and Computer Graphics, 2017, 29(6): 1128-1134.)
[4] HILAGA M, SHINAGAWA Y, KOHMURA T, et al. Topology matching for fully automatic similarity estimation of 3D shapes [C]// SIGGRAPH '01: Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 2001: 203-212.
[5] DU H, QIN H. Medial axis extraction and shape manipulation of solid objects using parabolic PDEs [C]// SM '04 Proceedings of the 9th ACM Symposium on Solid Modeling and Applications. Aire-la-Ville, Switzerland: Eurographics Association, 2004: 25-35.
[6] 王飛,张树生,白晓亮,等.拓扑和形状特征相结合的三维模型检索[J].计算机辅助设计与图形学学报, 2008, 20(1): 99-103.(WANG F, ZHANG S S, BAI X L, et al. 3D model retrieval based on both the topology and shape features [J]. Journal of Computer-Aided Design and Computer Graphics, 2008, 20(1): 99-103.)
[7] LI F, DAI Q, XU W, et al. Statistical modeling and many-to-many matching for view-based 3D object retrieval [J]. Signal Processing Image Communication, 2010, 25(1):18-27.
[8] GAO Y, DAI Q, WANG M, et al. 3D model retrieval using weighted bipartite graph matching [J]. Signal Processing: Image Communication, 2011, 26(1): 39-47.
[9] LIPMAN Y, CHEN X, DAUBECHIES I, et al. Symmetry factored embedding and distance[J]. ACM Transactions on Graphics, 2010, 29(4): Article No. 103.
[10] SAHILLIOGLU Y, YEMEZ Y. Minimum-distortion isometric shape correspondence using EM algorithm [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2203-2215.
[11] SUN J, OVSJANIKOV M, GUIBAS L. A concise and provably informative multi-scale signature based on heat diffusion [J]. Computer Graphics Forum, 2009, 28(5): 1383-1392.
[12] AUBRY M, SCHLICKEWEI U, CREMERS D. The wave kernel signature: a quantum mechanical approach to shape analysis [C]// Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops. Washington, DC: IEEE Computer Society, 2011: 1626-1633.
[13] 姜巍,徐凯,程志全,等.一种通用的局部内蕴对称检测算法[J].计算机辅助设计与图形学学报,2013,25(7):974-979.(JIANG W, XU K, CHENG Z Q. et al. A generalized algorithm for partial intrinsic symmetry detection [J]. Journal of Computer-Aided Design and Computer Graphics, 2013, 25(7): 974-979.)
[14] 匡振中,李宗民,田伟伟,等.热模态特征与非刚体模型检索[J].计算机辅助设计与图形学学报,2015,27(8):1426-1433.(KUANG Z Z, LI Z M, TIAN W W, et al. Modal feat feature and non-rigid 3D model retrieval [J]. Journal of Computer-Aided Design and Computer Graphics, 2015, 27(8): 1426-1433.)
[15] LAU L C, NAOR J S, SALAVATIPOUR M R, et al. Survivable network design with degree or order constraints [J]. SIAM Journal on Computing, 2017, 39(3):1062-1087.
[16] 朱利,邱媛媛,于帅,等.一种基于快速k-近邻的最小生成树离群检测方法[J].计算机学报,2017,40(12):2856-2870.(ZHU L, QIU Y Y, YU S, et al. A fast kNN-based MST outlier detection method [J]. Chinese Journal of Computers, 2017, 40(12): 2856-2870.)
[17] GAL R, COHEN-OR D. Salient geometric features for partial shape matching and similarity [J]. ACM Transactions on Graphics, 2006, 25(1): 130-150.
[18] HAN L, HU J Y, LI L. Volume-based skeleton extraction [J]. ICIC Express Letters, 2014, 8(3): 859-865.
韩丽, 胡江月. 体积分布的三维模型形状分析方法[J]. 计算机工程与应用, 2015, 51(23):195-198.(HAN L, HU J Y. Shape analysis method of 3D models based on volumetric distribution [J]. Computer Engineering and Applications, 2015, 51(23): 195-198.)
[19] SHAPIRA L, SHAMIR A, COHEN-OR D. Consistent mesh partitioning and skeletonisation using the shape diameter function [J]. Visual Computer, 2008, 24(4): 249-459.
[20] SHAPIRA L, SHALOM S, SHAMIR A, et al. Contextual part analogies in 3D objects [J]. International Journal of Computer Vision, 2010, 89(2/3): 309-326.
[21] SHILANE P, MIN P, KAZHDAN M, et al. The Princeton shape benchmark [C]// SMI '04Proceedings of the 2004 Shape Modeling Applications. Washington, DC: IEEE Computer Society, 2004: 167-178.
[22] YANG Q. A non-local cost aggregation method for stereo matching [C]// CVPR '12 Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2012: 1402-1409.
[23] AFSAL S, RAFEEQ A K, JOTHYKUMAR J, et al. A novel approach for palm print recognition using entropy information features [C]// Proceedings of the 2016 International Conference on Wireless Communications, Signal Processing and Networking. Piscataway, NJ: IEEE, 2016.
AFSAL S, RAFEEQ A K, JOTHYKUMAR J, et al. A novel approach for palm print recognition using entropy information features [EB/OL]. [2018-07-12]. https://ieeexplore.ieee.org/document/7566374/.
[24] 王年,周梅菊,张江,等.基于最小生成树的LAPLACE谱图像匹配算法[J].系统仿真学报,2009,21(17):5481-5485.(WANG N, ZHOU M J, ZHANG J, et al. Laplacian spectrum image matching algorithm based on minimum spanning tree [J]. Journal of System Simulation, 2009,21(17): 5481-5485.)
[25] 韓丽,颜震,徐建国,等.基于显著特征谱嵌入的三维模型相似性分析[J].模式识别与人工智能,2015,28(12):1119-1126.(HAN L, YAN Z, XU J G, et al. Three-dimensional model similarity analysis based on salient features spectral embedding [J]. Pattern Recognition and Artificial Intelligence, 2015, 28(12): 1119-1126.)
[26] CHUI H, RANGARAJAN A. A new point matching algorithm for non-rigid registration[J]. Computer Vision and Image Understanding, 2003, 89(2):114-141.
[27] MYRONENKO A, SONG X. Point set registration: coherent point drift [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2262-2275.