基于HPM视角的初等数论课程教学探究

张四保

(喀什大学 数学与统计学院， 新疆 喀什 844008)

“数学是科学的皇后，而数论是数学皇冠”[1]，对于数论在数学中的地位，高斯曾作过如此评价。初等数论是研究数，尤其是研究整数性质的一个最古老的数学分支，它所使用的方法初等与朴素的。在数论中有的命题表述极为简洁，而要证明命题却极为艰难。如哥德巴赫猜想、孪生素数猜想等大量的“皇冠上的明珠”等难题尚未解决。初等数论在诸多理论中的命题有着广泛的应用，如信息安全、代数编码、密码学等。“初等数论”课程包含了现行基础教育新课程标准下高中数学选修系列4“初等数论初步”模块的全部内容[2]，同时整数的整除、公因数、公倍数等内容都是现行小学数学的主要内容，师范院校的师范专业数学与应用数学专业、小学教育专业把“初等数论”课程作为专业主干课程。任课教师如何使得学生对于“初等数论”课程易学、易理解、易掌握，已成为这一课程教学改革的一个迫切需要解决的问题。基于HPM视角的课程教学，为解决问题提供了一个行之有效的途径。

何为HPM? HPM是History and Pedagogy of Mathematics的简写，它源自第二届国际数学教育大会上的一个工作小组，是专门研究数学史与数学教育之间关系的组织。主要的研究内容如图1所示，其目的是通过研究数学教学过程中的应用数学史，提高数学教育质量与成效。

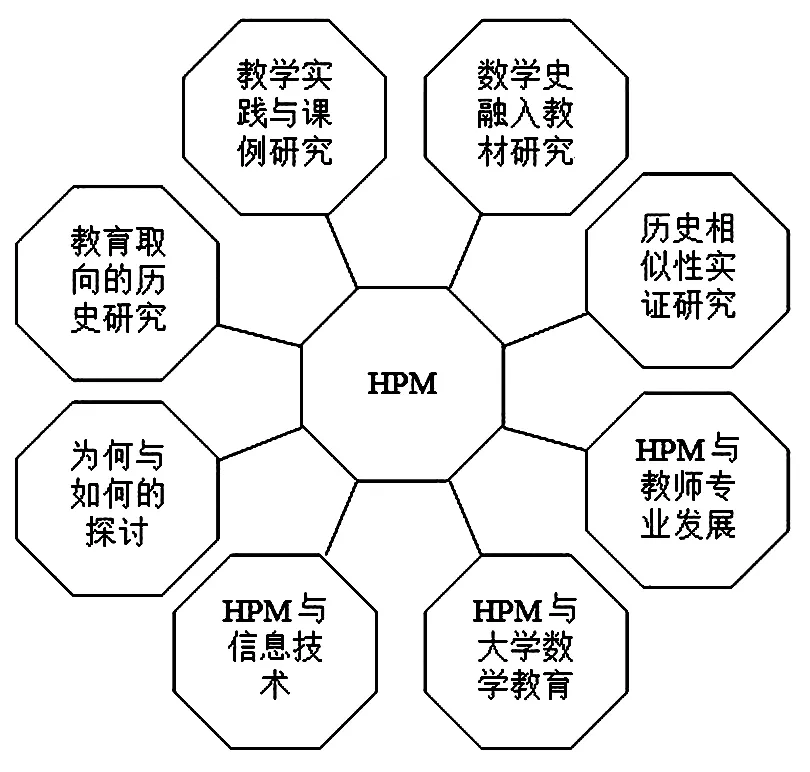
图1 HPM的主要研究内容

1 HPM对初等数论课程教学的作用

1.1 有助于激发学生学习初等数论课程的兴趣

HPM的先驱者卡约里指出：“如果用历史轶事点缀枯燥的证明和计算，学生的兴趣就会大大增加……”也就是说一旦一个人对某一事物产生了浓厚的兴趣，他就会主动地去求知、探索与实践，并在求知、探索与实践的过程中体验其中的乐趣。同样，学习的过程也是如此，若学生对某一课程产生了浓厚兴趣，学生就会主动地去学习这一课程；反之，就会倦怠这一课程。2018年，教育部发布了《教育部关于狠抓新时代全国高等学校本科教育工作会议精神落实的通知》，文件要求狠抓本科教学，淘汰“水课”、打造“金课”。学生几乎不听课甚至逃课，这种课程就是“水课”的特征之一。出现“水课”的一个最主要的原因是任课教师讲课的方式过于呆板，照本宣科，甚至读课本，课程气氛枯燥，任课教师没有调动起学生的学习兴趣。而初等数论课程的内容较为陈旧且理论性很强，若教学方式方法单一，很难引起学生的学习兴趣。自然课程的教学效果就是事倍功半的，它距离“水课”就不远了。若在教学过程中，任课教师适时、适当、适量引入与教学内容有关的历史资料，激发学生对课程的学习兴趣，就会达到事半功倍的教学效果。

1.2 有助于提高学生对初等数论知识体系了解

数学知识主要体现在概念、思想与方法之上，思想与方法是对知识的再概括与再凝练。在讲授初等数论课程过程中，适当介绍前人进行探索的历史背景，了解前人的研究方法，透过现象看本质，可以加深学生对一些知识体系的了解，感受前人研究创造的激情。

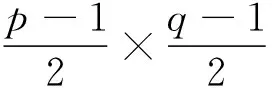
2 基于HPM视角的初等数论课程某些内容的实践教学

2.1 不定方程

不定方程是指未知数的个数多余方程个数的方程(组)。在讲解本章内容时，可以将以下史料融入课堂教学过程中。

古希腊亚历山大后期的重要学者和数学家丢番图，在撰写的用纯分析的途径处理数论与代数问题的《算术》(Arithmetic)中，主要是以不定方程的求解而著称。在此之前，阿基米德就接触过类似问题，提出了“牛群问题”(The cattle problem)。但丢番图是对不定方程问题作深入研究的第一人，因而也将不定方程称为“丢番图方程”。

在《算术》中有一个出名的不定方程问题：将一个已知的平方数分为两个平方数。这一问题之所以出名，主要是因为大约在1637年前后，“业余数学家之王”费马在阅读《算术》拉丁文译本时，对这一问题作了个边注写道，“将一个立方数分成两个立方数之和，或一个四次幂分成两个四次幂之和，或者一般地将一个高于二次的幂分成两个同次幂之和，这是不可能的。关于此，我确信已发现了一种美妙的证法 ，可惜这里空白的地方太小，写不下”，从而引出了“引无数英雄竞折腰”，耗时300多年才被解决的举世瞩目的“费马大定理”。

我国是研究不定方程最早的国家。大约成书于公元前1世纪的数学巨著《九章算术》中，有一道涉及不定方程的“五家共井”的问题。五家共井，甲二绠(汲水用的井绳)不足，如(接上)乙一绠；乙三绠不足，如丙一绠；丙四绠不足，如丁一绠；丁五绠不足，如戊一绠；戊六绠不足，如甲一绠，皆及，这标志我国很早就对不定方程理论有了系统研究。而这样相同的问题在13世纪意大利斐波那契《算经》与15世纪阿尔·卡西《算术之钥》中都曾出现过。

2.2 中国剩余定理

中国剩余定理又称孙子定理，因它最早记载在我国古代数学著作《孙子算经》，它是数论中的一个重要且广泛应用的定理，其内容如下：

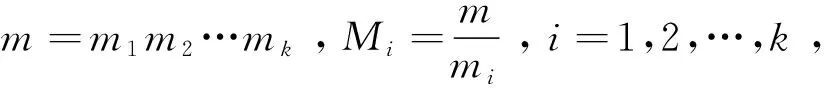
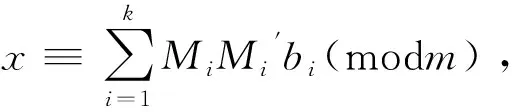
对于涉及这部分的内容，任课教师可适当地讲解一下以下史料。大约公元4世纪，我国古代重要的数学著作《孙子算经》记载着“物不知数”问题。今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？ 答曰“二十三”。这就是今天关于一次同余式组的解法问题。我国宋代大数学家秦九韶进一步推广了“物不知数”问题，开创了对一次同余式理论的研究工作。秦九韶在《数书九章》提出了“大衍总数术”，系统阐述了求解一次同余式组的一般方法，其中最关键的是“大衍求一术”，这是秦九韶对古历算家在求历法上元的总结。到了18、19世纪，欧拉与高斯分别对一次同余式组进行了深入的研究，获得了与秦九韶“大衍求一术”相同的定理。1876年德国马蒂生指出秦九韶的求解一次同余式组方法与高斯算法是一致的，这才引起欧洲对这一问题的重视。对于“物不知数”问题，我国明代数学家程大位在《算法统宗》(《新编直指算法统宗》)一书中用歌诀形式给出了解法：三人同行七十稀，五树梅花廿一枝，七子团圆正半月，除百零五便得知。其大意是用被3除的余数乘以70，用被5除后的余数乘以21，用被7除后的余数乘以15，然后相加，如大于105，便一次次地减去105，直至小于105为止。

2.3 素数

素数在整数理论中所占的地位是很重要的。根据算术基本定理，设整数a>1，a能被唯一的分解成a=p1p2…pk，其中pi(1≤i≤k)是满足p1≤p2≤…≤pk的素数，可以说素数是构成整数的基本单元。在数论中涉及有关素数的难题是很多的。任教者可适当讲解有关素数一些难题的研究进展情况，让学生直接与难题“对话”，去揭开难题的“面纱”。

梅森素数：梅森素数是形如2P-1的素数，其中P为素数，它是以17世纪法国数学家马林·梅森的名字命名，并记为MP。2300多年前，古希腊数学家欧几里得在《几何原本》中证明了素数的个数是无穷的，并提出一些素数可写成2P-1(其中P也是素数)的形式。自梅森素数提出以来，到目前为止只已发现了51个。第51个梅森素数M82589933于2018年12月7日由Patrick Laroche利用“互联网梅森素数大搜索(GIMPS)”项目被发现，它的位数高达24 862 048位，它是当今所知的最大素数。在探索的过程中出现了很多有趣的事情，如“梅森猜测”“欧拉是我们每一个人的老师”“一言不发的演讲”“美国伊利诺伊大学发行的纪念邮戳”“周氏猜测”神奇的书《2017年最大の素数》、研究梅森素数的重大意义等。任课教师可以选择性地讲解，让学生对梅森素数有初步的认识，也可能会产生意想不到的结果。

哥德巴赫猜想：1742年6月7日，哥德巴赫在给欧拉的一封信当中提出了一个假设：每个偶数是两个素数之和，每个奇数是三个素数之和。这就是闻名遐迩的哥德巴赫猜想。对于哥德巴赫给出的这一命题，1742年6月30日欧拉在给哥德巴赫的回信中给予了肯定。同时在回信中，欧拉也提出了另一个他也没能证明的命题：任何一个大于2的偶数都是两个素数之和。哥德巴赫猜想自1742年被提出来以后，直到20世纪初才有本质性的研究进展。对于奇数哥德巴赫猜想，1937年苏联数学家维诺格拉多夫利用圆法和指数和估计给出了证明，这是哥德巴赫猜想证明的第一个实质性的突破。而对于偶数哥德巴赫猜想的研究进展，主要是依靠改进筛法来取得。在哥德巴赫猜想研究领域中，我国是占据着领先地位的。在哈代名下从事数论研究的数学家华罗庚参与中国科学院数学研究所的筹建，并于1952年出任所长。1953年，华罗庚组织领导哥德巴赫猜想讨论班，并取得了丰硕的成果，这就包括王元的成果与潘承洞的成果，尤其是陈景润的成果。1966年，数学家陈景润宣布证明了“1+2”。后经改进，其“1+2”的详细证明于1973年发表在《中国科学》，后被国际数学界公认是“筛法理论的光辉顶点”。他的成果被国际数学界称为“陈氏定理”，写进美、英、法、苏、日等六国的许多数论书中。因这一成就，1978年他与王元、潘承洞共同获得国家自然科学奖一等奖，这个成果的水平至今都无人超越。

3 结语

本文只是列举了几个有关初等数论课程中所涉及数学史方面的内容，而这一方面的内容是很多的，这需要我们教育者认真地去收集与挖掘。HPM视角下将数学史料渗透于初等数论课程实践教学，可将枯燥的课堂生动化，这将有助于提高学生对理论知识本质的理解，增强学生自主学习的主动性，提升课堂教学效果，同时也可以使学生体会到数学史的教育价值。但是，需要指出的是，在具体的实践教学过程中，不能一味地将数学史料进行堆砌，而是要“活用活讲”，这样才能收到预期的教学效果。