基于Web 的复杂网络可视化仿真平台VPCN 的设计与实现∗

王月明 张 琨 张佳慧 蔡 颖 麻孟越

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

复杂网络［1］是指具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络［2］。复杂网络科学研究的是各不相同的复杂网络之间的共性和处理它们的普适方法，利用分析实际网络过程中产生的共性的概念、方法和理论，可以反过来为各种实际网络的分析与设计提供宏观指导和具体手段。复杂网络可视化仿真平台将成为研究复杂网络的基础和必不可少的重要工具，仿真平台的设计与实现已成为复杂网络研究的热点。现如今，国外知名的复杂网络可视化仿真平台包括Cytoscape、Netdraw、Matlab、Pajek 等［3］，为我国研究学者研究复杂网络带来了新的思维和良好的支持［4］。但是这些平台具有一定的应用背景，源代码不开放，二次开发难度较大，且大部分是基于单机版本，运行效率低，不能较好地处理大规模复杂网络的参数计算和特性分析。因此，本文基于Web 技术，自主设计和实现了一个复杂网络可视化仿真平台，并通过实际应用，验证了平台的有效性和可靠性。

2 传统复杂网络可视化与基于Web的复杂网络可视化研究概述

2.1 传统的复杂网络可视化技术

传统的复杂网络可视化平台［5］使用如VC++、Java等编程语言中的图形绘制库，在程序窗体之中调用图形绘制函数分别绘制网络点和线来实现网络可视化。关于图形绘制库，在VC++中常常使用CGraph，在 Java 中则是 Graphics2D，两者的思路都是在窗体类创建的窗体内部绘制网络图形，并在窗体的文本显示区域输出运行结果。

经过长时间的VC++、Java 复杂网络平台的使用和对平台代码的调试，发现传统复杂网络可视化的效果受图形绘制库的性能影响很大，在网站规格较大的时候显示会有一定延迟。而且由于编程语言的特点，调用图形绘制函数的代码往往和正常的网络参数计算代码交叉在一起影响识别，增加了图形显示的工作量，影响了基于复杂网络的可视化显示。

2.2 基于Web的复杂网络可视化技术

基于Web 的复杂网络可视化仿真平台的核心在于利用具有开放式接口的Web图形显示服务，来为复杂网络可视化提供有效支持。

在数据运算方面，基于Web的复杂网络可视化仿真平台使用了J2EE技术为Web界面提供数据支持。利用Java 的多种技术实现数据处理算法的区分和插件式管理，对应于Web界面的每类功能能够有对应的功能模块处理相关数据。

为加速数据处理算法的运算，本平台将计算规模扩大，使用Spark集群，采用了一种适用于网络参数计算的高效并行作业执行框架。网络参数计算作业提交后，根据各个节点的状态，作业调度器将网络参数计算任务分割并提交到空闲节点上并行执行。

3 基于Web 的复杂网络可视化仿真平台（VPCN）的设计

3.1 总体设计框架

本平台支持真实拓扑、典型网络拓扑的自动导入和网络拓扑的生成［6］，支持对网络拓扑的动态调整和关键节点的识别与显示，支持网络度分布、聚集系数、中介中心性、节点中心度、网络直径、网络最短路径参数等拓扑属性参数［7］的计算，网络拓扑规模最大可支持6500 个节点，并能够根据属性参数自动挖掘关键节点。本平台总体设计框架如图1所示。

图1 VPCN总体设计框架

3.2 功能模块

VPCN 的功能模块如图2 所示，具体包括四大功能模块:复杂网络生成导入模块、复杂网络调整模块、复杂网络参数计算模块和仿真结果表现模块。

图2 VPCN功能模块

1）复杂网络生成导入模块:复杂网络生成导入模块在VPCN 仿真平台启动后，用于为整个复杂网络仿真进行网络数据生成和导入，包括经典随机网络生成和真实交通网络导入。

2）复杂网络调整模块:复杂网络调整模块是在复杂网络生成或导入后对复杂网络点和边进行调整的模块，用于为复杂网络仿真的细节更改提供可视化支持。

3）复杂网络参数计算模块:复杂网络参数计算模块负责计算复杂网络的各种参数，在实现时具体分为两类参数。一类是复杂网络基本参数，包括度分布、网络直径、网络最短路径、中介中心性等；另一类是一些用于复杂网络及节点重要性、演化等内容研究所设计的扩展参数，包括节点中心度、聚集系数、最大邻居连通度、最大邻居连通密度、聚集系数等。

4）仿真结果展示模块:仿真结果展示模块是对整个仿真平台输出结果表现方式的确定，目前采用了两种输出方式表现整个仿真结果。

（1）将结果输出至指定的文件:这种表现方式是将一些计算的参数结果和仿真过程中的信息保存至指定的文件，便于用户的研究分析和事后处理；

（2）在可视化图形界面表现结果:在仿真结束后，可在复杂网络拓扑窗口中直接显示一些结构，例如，标出重要节点、显示网络结构信息等，给用户一种直观的效果。

4 基于Web 的复杂网络可视化仿真平台（VPCN）的实现

4.1 复杂网络的基本定义以及关键类设计

定义1:复杂网络基本模型。复杂网络用简单连通图G=(V ,E )表示。其中，图中的节点集V={v1,v2,…,vn} 代表节点集合；n= |V |表示节点的总数。 复杂网络的边（ 连接）集为E={e1,e2,…,em} ，m= |E |表示整个复杂网络的边的总数［8］。对每条边 es∊E(1 ≤ s ≤ m )，在 V 中有一对节点(vi,vj)(1 ≤i ≤n,1 ≤j ≤n )与之对应。

定义2:关键节点。复杂网络中相对于其它点具有较高价值的点称为关键节点，点的价值的评价标准不同，对应的关键节点也会不同。对于无向网络，常见的点的价值评价标准有度分布、中介中心性、聚集系数等。在公共交通中，站点抽象成的点的价值，表示该站点相对于其它站点在结构上有着特殊的重要性［9］。其度数越大，表明经过的公交路线越多，往往重要性也就越高。

根据上述定义，设计如下。

4.1.1 关键类设计

在复杂网络中，点、边以及图的类的设计往往对复杂网络仿真平台的设计有着重要的作用，因此设计点、边以及图的类如下。

class Node//网络点的类

｛

String name；//节点名称

double lng；//节点经度

double lat；//节点纬度

｝

class Line//网络边的类

｛

Node［］nodelist；//线路节点序列

int nodeinline；//节点数量

String linename；//线路名称

｝

class Map//网络图的类

｛

int nodenum；//网络节点总数

int linenum；//网络线路总数

Line［］linelist；//网络线路序列

int［］［］map；//网络邻接矩阵

int［］［］neighbor；//网络邻接表

｝

4.1.2 复杂网络拓扑展示区域设计

为有效实现复杂网络仿真平台的可视化，本平台利用百度地图技术，将复杂网络拓扑中的节点分布于百度地图的背景所规定的大小的笛卡尔坐标系上，生成随机图时将分别产生随机浮点数作为各个节点的坐标，实现复杂网络拓扑的可视化。本平台使用的百度地图版本为2.0 版，调用Map（）函数构造百度地图显示区域，使用PointCollection（）函数支持海量点的显示，利用Polyline（）函数实现边的绘制，通过Label（）函数展示网络的相关文本信息。设计成矩形区域可以适应人类的浏览习惯，且生成随机点的方法便于计算以及后续将随机点与数据结合进行处理，还可以在保证显示效果的同时提高图形的显示速度。

4.2 复杂网络的关键算法设计

4.2.1 无标度随机网络生成算法

无标度随机网络的无标度性质用于描述大型复杂网络整体上严重不均匀分布的一种内在性质，是随机网络的一种经典类型。

目前常用的无标度随机网络生成算法为B-A无标度网络生成算法，该算法中节点连接选择的择优概率公式为

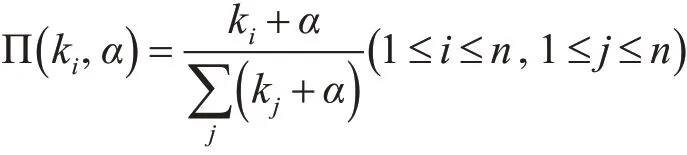
其中n 代表网络中的节点总数，ki代表第i 个点在网络中的连接数，α 为常数，代表初始连接数。本平台采用以上的择优概率公式提供了生成无标度随机网络的一种算法，算法步骤如下:

2）生成一个1到n 之间的随机整数 a，作为第一个点的序号；

4）判断 (va,vb)节点对所对应的边是否存在，即rab和rba为是否为1，如果存在回到步骤2）；

5）将 (va,vb)节点对所对应的边添加进连通数组R，即设置rab和rba为1，同时更新连接概率数组 P ，即 pa和 pb自增1；

6）判断添加的边的数量是否到达设定的最大值，是则网络生成技术，否则回到步骤2）继续。

4.2.2 复杂网络参数计算算法-中介中心性

复杂网络参数计算算法常见的有度分布、聚集系数、中介中心性、节点中心度、网络直径、网络最短路径等［10］，下面以中介中心性为例介绍本平台的复杂网络参数计算流程。

复杂网络中点的中介中心性反映途经这一节点的最短路径数目在全部路径中所占的比例，体现了节点对于整个网络的最优交通路径的影响力，对于复杂网络的优化研究具有重要意义。本平台提供了生成计算复杂网络中介中心性的一种算法，复杂网络其中最短路径数计算步骤如下:

点i 和节点 j 之间存在的最短路径数量，初始值为rij，最短路径长度矩阵，其中lij(1 ≤i ≤ n,1 ≤ j ≤ n )表示节点 i 和节点 j 之间存在的最短路径数量，初始值为0 ，邻居矩阵，其中hij(1 ≤ i ≤ n,1 ≤ j ≤ n )表示节点i 的第 j 个邻居的序号，空值为0，初始化节点标志位 p，表示当前访问的节点序号，初始值为1；

2）新建一个空的队列结构Q，满足先进先出原则，初始化访问标志位数组T={t1,t2,…,tn} ，其中ti(1 ≤i ≤n )表示第 i 个节点已经被访问，初始值为0，第 p 个点进入队列结构Q；

3）队列结构Q为空则转至步骤7），非空则队首元素x出队，按照邻居矩阵H 遍历该节点的邻居节点值hxq(1 ≤ q ≤ n )，tx置 1；

4）邻居节点 hxq如果为0，则跳转到步骤3），否则到步骤5）；

5）邻居节点hxq与节点 p 是否已经存在最短路径，是则转至步骤7）；

6）初始化最短路径长度矩阵L 中lpq值为lpx+1，最短路径计数矩阵C 中的cpq值为cpx；

7）当前搜索路径长度lpx+1与最短路径长度矩阵L 中lpq比较是否相等，是则更新最短路径计数矩阵 C ，即设置 cpq自增 cpx，q 自增 1，转至步骤4）；

8）p 是否为n，是则运算结束，否则 p 自增1，回到步骤2）。

根据以上流程计算出的最短路径数，根据中介中心性的计算方法，节点 p 的中介中心性计算公式为

公式中用到的cij、lij等数值取自最短路径计数矩阵C 和最短路径长度矩阵L，经过该公式计算可以求得复杂网络中介中心性的值。

5 复杂网络节点重要性评价方法仿真实例

本节通过多种复杂网络节点重要性评价方法的仿真实例对本仿真平台的有效性进行说明。仿真平台中内置了北京公交网络数据，该数据来源为百度地图 api（http://map.baidu.com/）和图吧公交（http://bus.mapbar.com），对北京公交站点和路线组成的复杂网络进行节点重要性评价。

该平台立足于公共交通的应用背景，故选用真实的北京公交网络进行网络的显示和网络参数的计算，平台可视化的效果如图3、图4所示。

图3 交通网络图

图3 所用的交通网络数据来源于北京市公交网络，选取了含有7504个节点和17667条边的数据进行显示。可以看到交通网络在地图背景下显得更为真实，实际加载时间和地图缩放延迟都体现了该可视化平台的实时性特点。同时网络的调整功能可以对网络进行一定的操作，如图中演示的网络节点删除功能。

图4 显示的是网络关键节点的可视化效果。参数运算部分运行完成后可以即时传至网页端表格显示，关键节点可以在信息计算完成的同时立即显示。

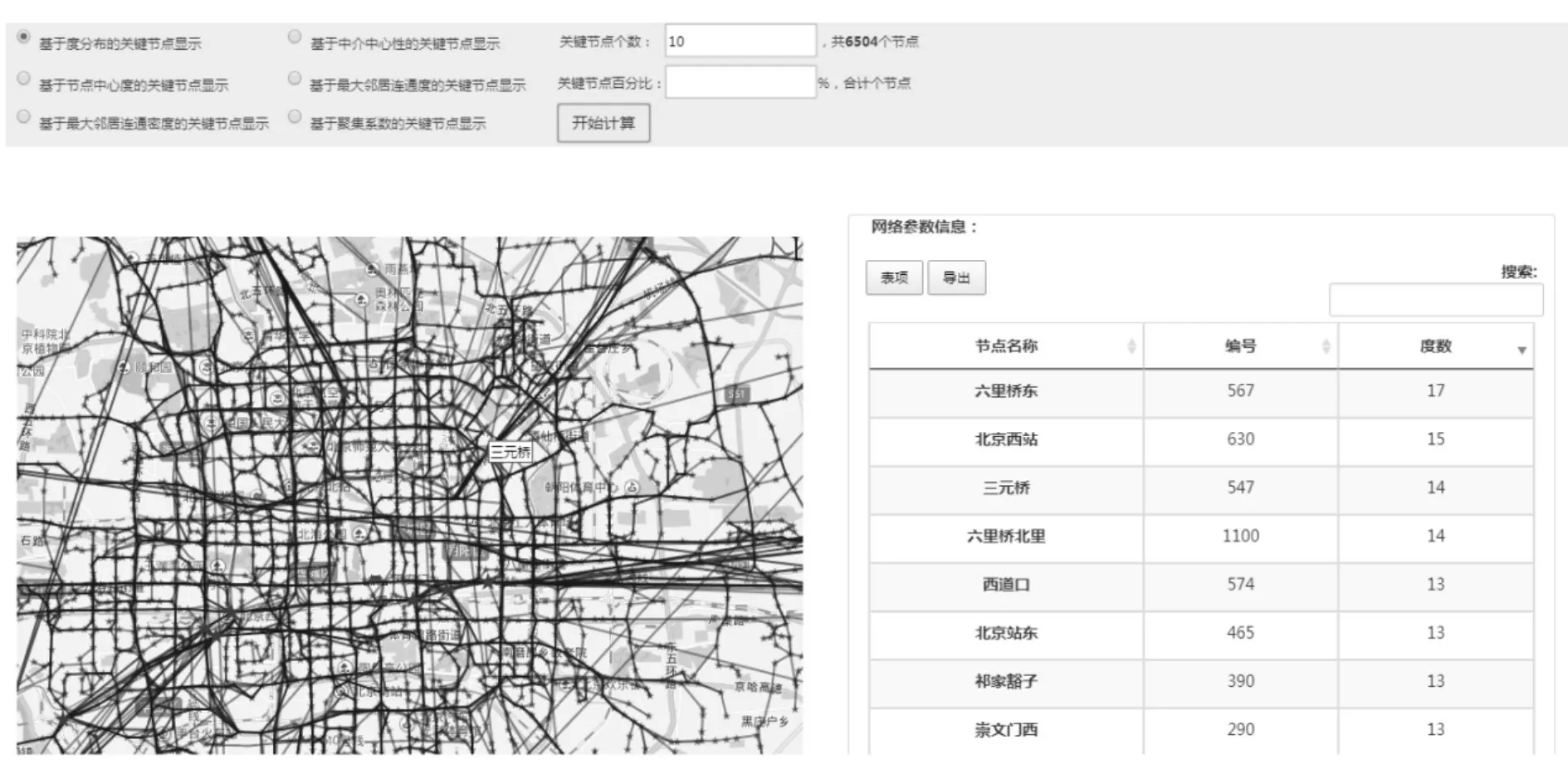
图4 关键节点显示图

本平台实验中选取网络度分布、聚集系数、中介中心性、节点中心度参数对北京市公交网络进行参数分析，得到参数计算结果如图5 所示，可以看出本平台能够有效发掘复杂网络关键节点的信息，通过序号和节点名称的形式准确查找到关键节点的位置，是一种高效且可视化效果优秀的复杂网络可视化仿真平台。

图5 复杂网络参数计算结果图

6 结语

从网络可视化效果可以看出，基于Web的复杂网络可视化仿真平台相对于传统的复杂网络可视化平台有着更好的显示效果，能够通过在网络图上添加网络相关信息的方式有效提升复杂网络的可视化效果，从而为公共交通的分析提供有效支持。

在网络性能方面，规模较大的网络可以实现较为流畅的显示，网络缩放功能也能够在保持操作流畅的情况下提升网络所能容纳的信息量，充分展现网络的利用价值，为公共交通的设计提供有效参考。

从拓展性角度上看，该基于Web的复杂网络可视化仿真平台和地理信息的结合度较高，比较适合网络按照地理位置分布并与地理信息有高度相关性的网络，除公共交通网络之外还有在电力网络、生物迁徙网络、病毒传播网络等等场景下的应用可能性。研究方向上，未来还将添加对于复杂网络抗毁性［11］的连通度［12］、复杂网络聚类算法［13］的改进［14］和数据场［15］的应用方面的研究。性能提升方面，为了应对超大规模网络上高复杂度算法的运算，未来将在Java平台的基础上改进连接Spark［16］大数据运算平台运算的部分以加快运算速度。