基于灾变因子的量子遗传算法研究∗

张秋艳 王默玉 申晓留 武书舟 闫丽娜 曹柳青

（华北电力大学控制与计算机工程学院 北京 102206）

1 引言

在现实生活中，许多优化问题要求人们不仅要计算出其极值，还要得出其最优值。这类问题对传统的算法造成的严峻的挑战。在这种情况下，越来越多的群智能算法相继的提出，遗传算法是由美国密歇根大学的John Holland 教授和他的同事与学生最早开始研究和应用的。是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应搜索算法［1］。简而言之，它使用了群体搜索技术，将种群（population）代表一组问题解，通过对当前种群施加选择（selection）、交叉（crossover）和变异（mutation）等一系列遗传算子（operator），从而产生新一代种群，并逐步使种群进化到包含近似最优解的状态。由于其思想简单、易于实现以及表现出来的健壮性，遗传算法赢得了许多应用领域，特别是近年来在问题求解、优化和搜索、机器学习、智能控制、模式识别和人工生命等领域取得了许多令人鼓舞的成就。

2000 年，K.H，HAN 等在文献中提出在遗传编码过程中加入量子的态矢量表达，首次创造性地提出了量子遗传算法并在量子旋转门的基础上，实现了个体染色体的基因调整策略，大大提高了量子遗传算法在量子计算机上运行的可能性。

2 量子遗传算法理论与方法

在量子遗传算法中，最重要的是量子编码和量子门的引入。量子编码是将染色体用量子的态矢量表示，使一条染色体表达为多个态的叠加，从而增加了种群多样性，使算法能够在较小的种群规模下求得最优解；而量子门的引入使算法具备了开发能力和探索能力，可以保证算法收敛［14～15］。目前，量子遗传算法被应用到了多个领域，如电网规划以及图像处理等［2～4，13］。

2.1 量子编码

在量子遗传算法中，使用了一种新颖的基于量子比特的编码方式，即用一对复数定义一个量子比特位，一个具有m 个量子比特位的系统可以描述为

其中，|αi|2+ |βi|2=1(i=1,2,…,m)。

量子比特位可以同时处于两个量子态的叠加态 φ =α0 +β1 中，如:其中 0 和 1 分别表示自旋向下态和自旋向上态，φ 为一种量子态的表示，式中 α 和 β 为复数，表示量子位状态的概率幅，| α|2i可看成量子处于自旋向下态的概率，| β|2可看成量i子处于自旋向上态的概率。

若有一个具有三个量子比特位的量子编码:

则该量子编码可以转换为如下形式的二进制编码。

即该量子编码转换为|000|、|001|、|100|、|101| 的概率分别为1/8、3/8、1/8、3/8。所以，该量子编码具有四个二进制编码的信息，显然这种编码方式能够使种群拥有更好的多样性，且随着 |α|2、| β|2ii趋于0 或1，染色体将收敛于一个单一态。因此，与遗传算法相比，量子遗传算法在较小的种群规模下就可以得到最优解。

2.2 量子门

量子门作为完成进化的操作机构，可以根据具体情况进行选取，目前已有多种量子门，按照量子遗传算法的特点，选择量子旋转门作为执行机构较为合适。

通过量子门变换矩阵可以实现种群的更新实际上量子门变换矩阵是一个可逆的归一化矩阵，即需要满足UU*=U*U=1。

常用的量子旋转门为

其中[α ,β]T为染色体中的第i 个量子位，θ 旋转iii角。

2.3 量子遗传算法流程

量子遗传算法首先取规模为N 的种群进行初始化，一般情况，种群中全部染色体的所有基因都被初始化为(1/ 2,1/ 2)；然后对初始种群每个个体实时一次测量，得到一个状态P（t），然后对这一组解进行适应度评估，记录下最佳最适应度个体作为下一步演化的目标值［5］。并实时记录最佳个体及其适应度值。具体算法基本步骤如下:

t=0

对Q（t）初始化

通过观察Q（t）的状态确定P（t）

评价P（t）保存中的最优个体

如果不满足终止条件

Begin

t=t+1 ；

通过观察Q（t）的状态确定P（t）

评价P（t）保存中的最优个体

用量子门U（t）更新Q（t）

保存P（t）中的最佳个体

直至满足终止条件

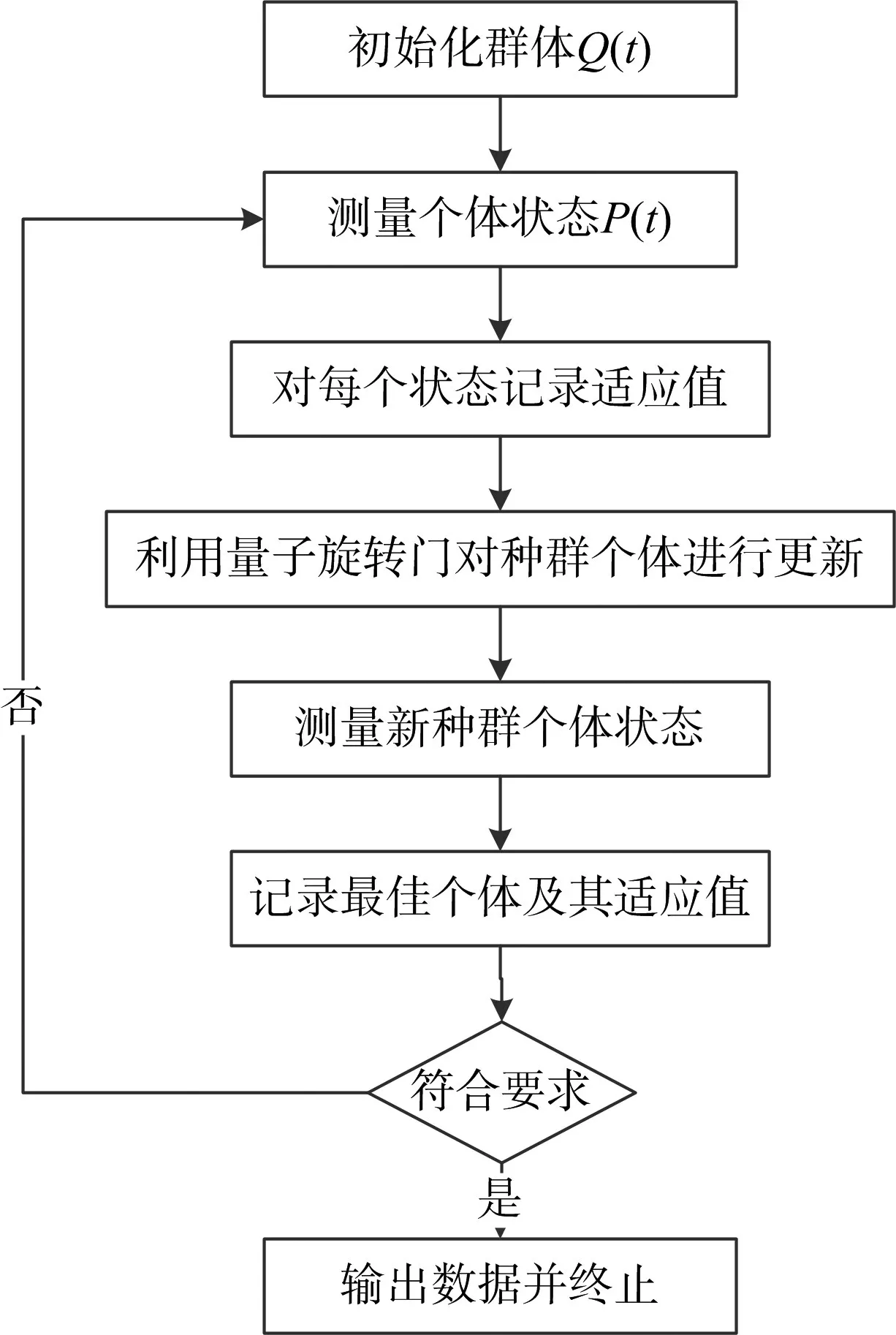
图1 量子遗传算法流程

2.4 灾变因子

为了进一步提高全局搜索性能，引入“灾变”概念到遗传算法中。在生物进化过程中，“灾变”就是外部环境的巨大变化，如冰河期、森林大火、大地震和瘟疫等，是对绝大多数生物的灭顶之灾，造成了大量物种或者个体的灭绝，只有个别适应能力特别强的物种或者个体得以生存，在“灾变”过后重新繁衍后代。显然“灾变”后幸存的物种或个体的生存能力更强［8～10］。

当经过若干代之后，算法中群体已经获得某个局部最优解，而此时的群体隐含着大量与该局部最优相关的信息，趋向于早熟收敛，依靠交叉和变异等遗传操作跳出来的可能性较小，这时可以引入“灾变”，除了原最好解留下来，其他个体重新随机产生，获得一些全局性的有效信息，以较大的概率得到远离原局部最优，使得在较小的群体规模下获得较大的多样性，则可以更有机会摆脱原先的局部最优解，因为现在的候选解往往不再局限于以前的某个角落了［11～12］。

灾变因子引入思路简示如下:

1）灾变次数初始化；

2）进行某阶段的遗传进化操作和适应度评估；

3）灾变次数增加1；

4）如果达到预定值则输出结果并结束，否则存当前最好解并返回第2）步。

2.5 基于灾变因子的量子遗传算法

当种群中个体之间的差别很小的时候，认为算法将要陷入不成熟收敛了，此时采用灾变算子来提高个体之间的多样性，以保证算法能够找到全局最优解。

灾变的实施也有很多的方法:1）突然增大变异率；2）保留最好解，重新初始化其他的个体；3）对不同的个体实施不同规模的变异。本文采用的是第二种方法。

基于灾变因子的量子遗传算法流程如图2。

图2 基于灾变因子的量子遗传算法

加入灾变因子后，当最优值保持一定次数后，则认为进化已经进入了不成熟的收敛阶段，设定灾变因子disater_factor，当最优值持续一定程度后，保留最优值并对种群进行新的初始化，确保算法跳出局部最优

3 实验对比

本文采用三个标准函数针对量子遗传算法与标准遗传算法作对比:

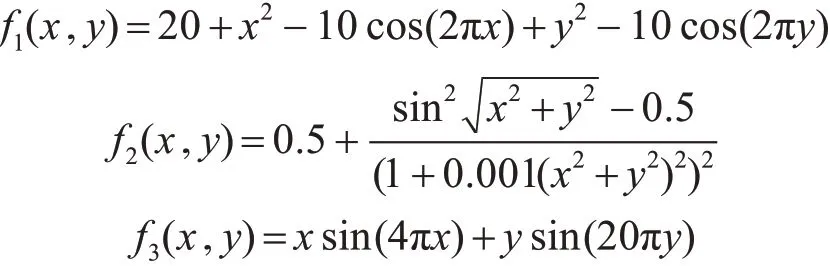
这几个典型的标准函数都具有全局极值点，并且有多峰值函数，有多个峰值陷阱，这样一般优化算法容易陷入局部收敛，用它们来比较各种算法的性能是合适的。在这里种群大小设置为40，最大遗传代数基础设置为100，分别测试标准遗传算法SGA 以及基于灾变因子量子遗传算法QGA 的寻优效果，结果如图4～6所示。

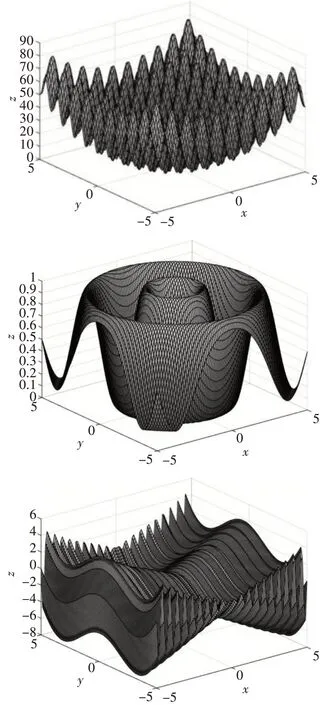
图3 测试函数空间曲面图

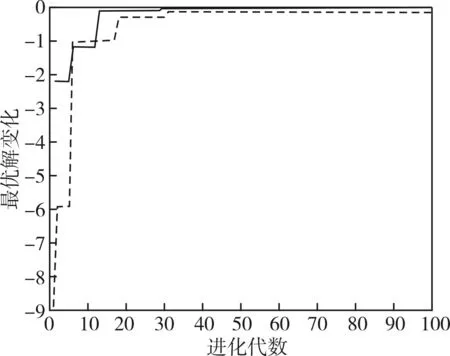
图4 F1函数进化代数与最优解变化

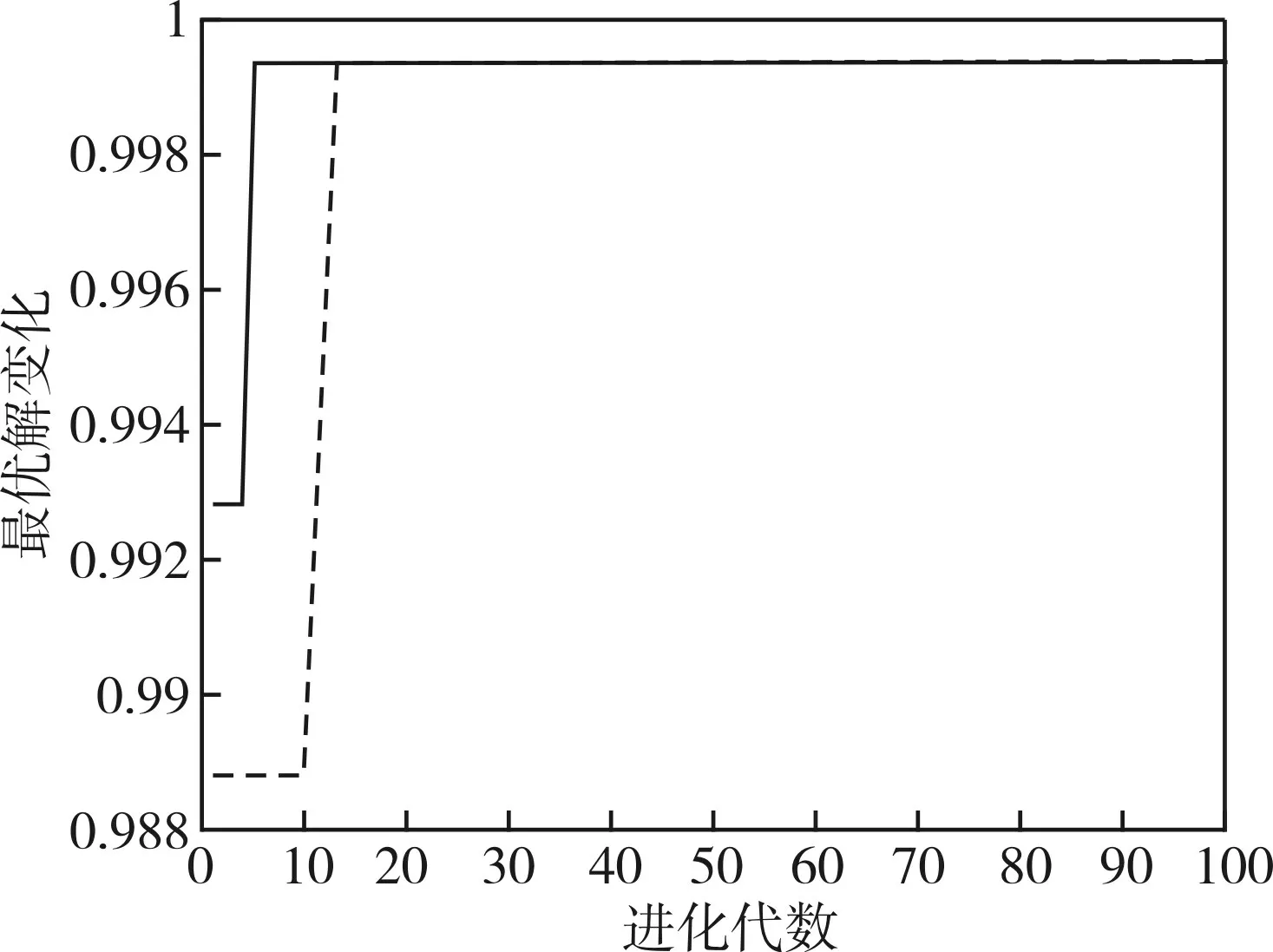
图5 F2函数进化代数与最优解变化

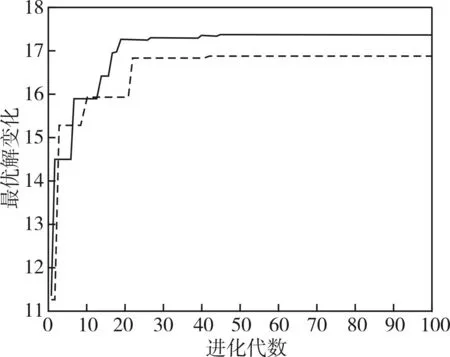
图6 F3函数进化代数与最优解变化

上图中，虚线表示标准遗传算法的最优解与进化代数的关系，实线表示基于灾变因子量子遗传算法的最优解与进化代数的关系。可以得出在多峰值函数寻优过程中，基于灾变因子量子遗传算法收敛速度快，寻优结论相比较之下要比标准遗传算法更加准确。标准遗传算法在多峰值情况下的寻优会出现过早收敛，无法调出局部最优的问题，寻优结果不稳定。相比较之下，基于灾变因子量子遗传算法使用量子门对种群进行更新，加入灾变因子，更快跳出局部最优，有效阻止了局部最优解的产生，由此可见，基于灾变因子的量子遗传算法与标准遗传算法相比，由于算法迅速地从某个局部区域中摆脱出来，并在新的解空间中进行继续的搜索，因而能大大改善了量子遗传算法的收敛性。

4 结语

基于灾变因子量子遗传算法是在遗传算法的基础上，将量子计算在计算方面的优势引入遗传算法里，并且引入了灾变因子，弥补了传统遗传算法的缺陷，它仍属于遗传算法的范畴，但比遗传算法的优化性能高。

本文是通过把基于灾变因子的量子遗传算法和遗传算法分别应用于三个测试函数进行仿真测试，对测试结果进行图表分析，然后得出结论。所选的三个测试函数都是具有峰值的函数。从实验的图表中可以得出:

1）基于灾变因子的量子遗传算法在对同一峰值函数进行测试求解，所求得的最优解的精确度会随着其迭代次数的增大而提高。

2）基于灾变因子的量子遗传算法对峰值函数进行测试求解时，在相同的迭代次数下，用量子遗传算法所求得的峰值函数的最大值的精确度要高于用遗传算法所求得。

这表明了量子遗传算法算法在连续空间优化的可行性和有效性，同时也表明了量子遗传算法算法具有良好的应用前景。