快速求解关联运动的速度
2019-07-30钟俊敏
钟俊敏
(江西省新余市第四中学,江西 新余 338000)
两个相互接触的物体的关联速度的求解,一直是关联运动的教学难点,又往往成为考查的重点.因为它能较好地检测学生对运动合成与分解的掌握程度,又能较好地甄别学生矢量运算能力.
关联体是指两个(或以上)相互关联的物体,通常由轻绳或轻杆系在一起,或直接挤压在一起运动.由轻绳(或杆)连接的两个物体沿着绳子(或杆子)方向的分速度相等,这类关联体运动比较形象,学生容易掌握.本文主要研究后者,即两个直接挤压接触在一起的物体的运动(如图1所示).将物体的实际运动(即合运动),分解成几个简单的分运动,逐个研究,找出其分运动的速度,再按其效果合成.如匀加速直线运动(位移):x=v0t+at2/2,分解为x1=v0t的匀速直线运动,与x2=at2/2的匀加速直线运动,两个运动分别进行,再将两个分运动合成.不在一条直线上时,按矢量的平行四边形定则合成.这样,教师讲解思路清晰,学生理解过程简单,能准确找出关联的关系,快速得出正确结果.
例1.如图1所示,将倾角为的θ楔型木块B放在光滑水平面上靠墙边处,并用手扶着,然后在木块和墙面之间放入一个小球A.放手让小球和木块同时由静止开始运动,某一时刻二者速度分别为vA和vB,则
(A)vA∶vB=1∶1.
(B)vA∶vB=sinθ∶cosθ.
(C)vA∶vB=cosθ∶sinθ.
(D)vA∶vB=sinθ∶tanθ.
解析:小球A的实际的速度vA(合运动)竖直向下,它的运动有两个效果,一是沿斜面向下的运动,设其速度v1,二是垂直斜面向下的运动,设其速度为v2,如图2(甲)所示,则有v2=vAcosθ.

图1

图2
楔形木块B的实际的速度vB(合运动)水平向右,它的运动也有两个效果,一是沿斜面向上的运动,设其速度v3,二是垂直斜面向下的运动,设其速度为v4,如图2(乙)所示,则有v4=vBsinθ.
又因二者在垂直斜面方面上紧紧地挤压在一起,则它们在垂直斜面方向上的分速度相等,于是有v2=v4.
由以上各式得vA∶vB=sinθ∶cosθ,故选(B).
这种解法要分解两个矢量,学生对一个矢量分解就不易理解.并且学生对于“两个物理沿弹力方向的速度相等”更不好理解.形成了思维障碍,导致了教学难点.
新解:运用运动的分解方法,把A球的运动分解成二个运动(如图3所示):A随B水平向右的匀速直线运动[如图3(甲)所示],速度为vB;A沿斜面B向下的匀速运动[如图3(乙)所示],速度为v,两个运动是同时进行的,故合速度vA与两个分速度矢量关系如图3(丙)所示.这样只有一个矢量图,几何关系明显,由vA∶vB=tanθ,得(B)正确.

图3
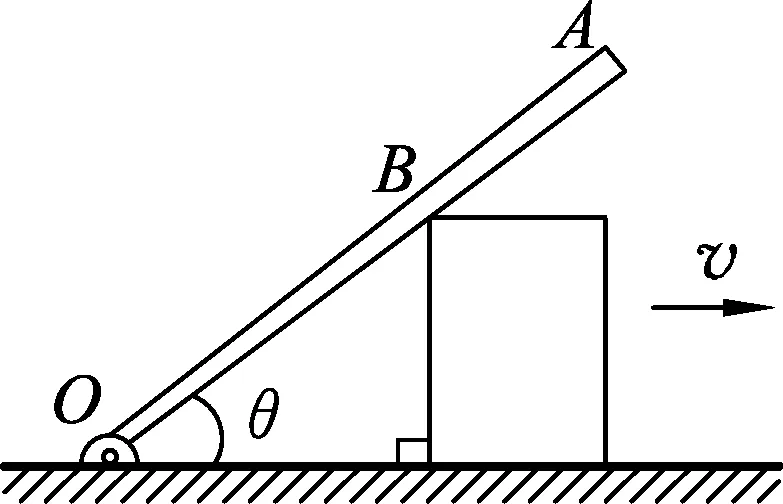
图4
练习1.如图4所示,一根长为L的轻杆OA,O端用铰链固定,轻杆靠在一个质量为M,高为h的物块上.若物块与地面的摩擦不计,杆上B点垂直杆的速度为v2,此时杆与水平方向的夹角为θ,求此时物块向右运动的速度v.
解析:将物体的运动分解为沿杆方向的平动v1,和沿O点转动,即切线方向垂直于杆的运动v2,如图5所示,可见v2=vsinθ.

图5

图6
例2.一个半径为R的半圆柱体沿水平方向向右以速度v0匀速运动.在半圆柱体上搁置一根竖直杆,此杆只能沿竖直方向运动,如图6所示.当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ时,求竖直杆运动的速度.
解析:由于半圆柱体对杆的弹力沿OP方向,所以将竖直杆向上的速度v沿OP方向和沿半圆的切线方向分解,如图7(甲)所示,将半圆柱体水平向右的速度v0也沿OP方向和沿半圆的切线方向分解,如图7(乙)所示.二者在垂直于接触面的方向上(即OP方向)的分速度相等,于是有:v0sinθ=vcosθ,解得v=v0tanθ.
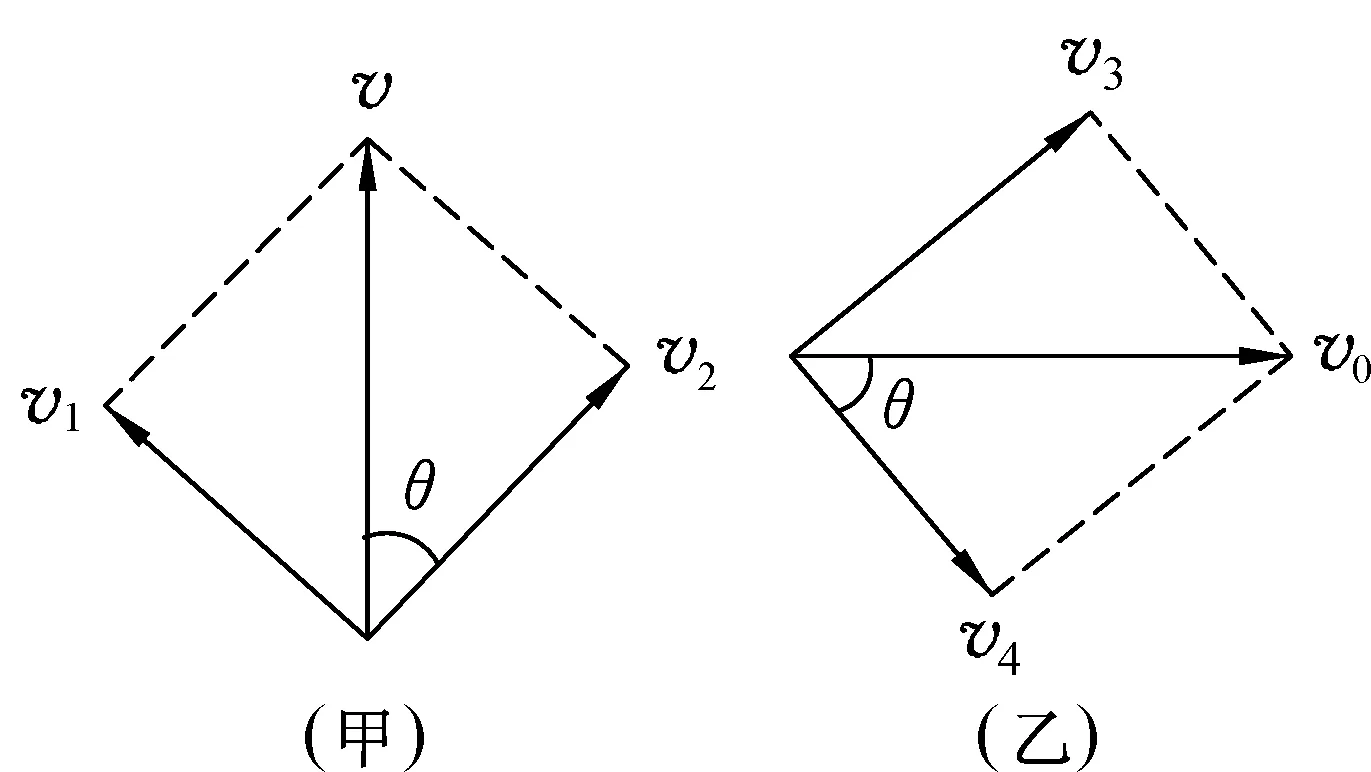
图7
这种解法同样要分解两个矢量,学生不易理解.
新解:将竖杆的运动分为二个运动:一个沿柱面做圆周(曲线)运动,速度v1与圆面相切,垂直于OP向上[如图8(甲)所示];杆与柱面共同向右平动,速度为v0[如图8(乙)所示],水平向右.而杆的实际运动(即合运动)竖直向上,大小为v,因为同时进行,故矢量图[如图8(丙)所示],得v=v0·tanθ.
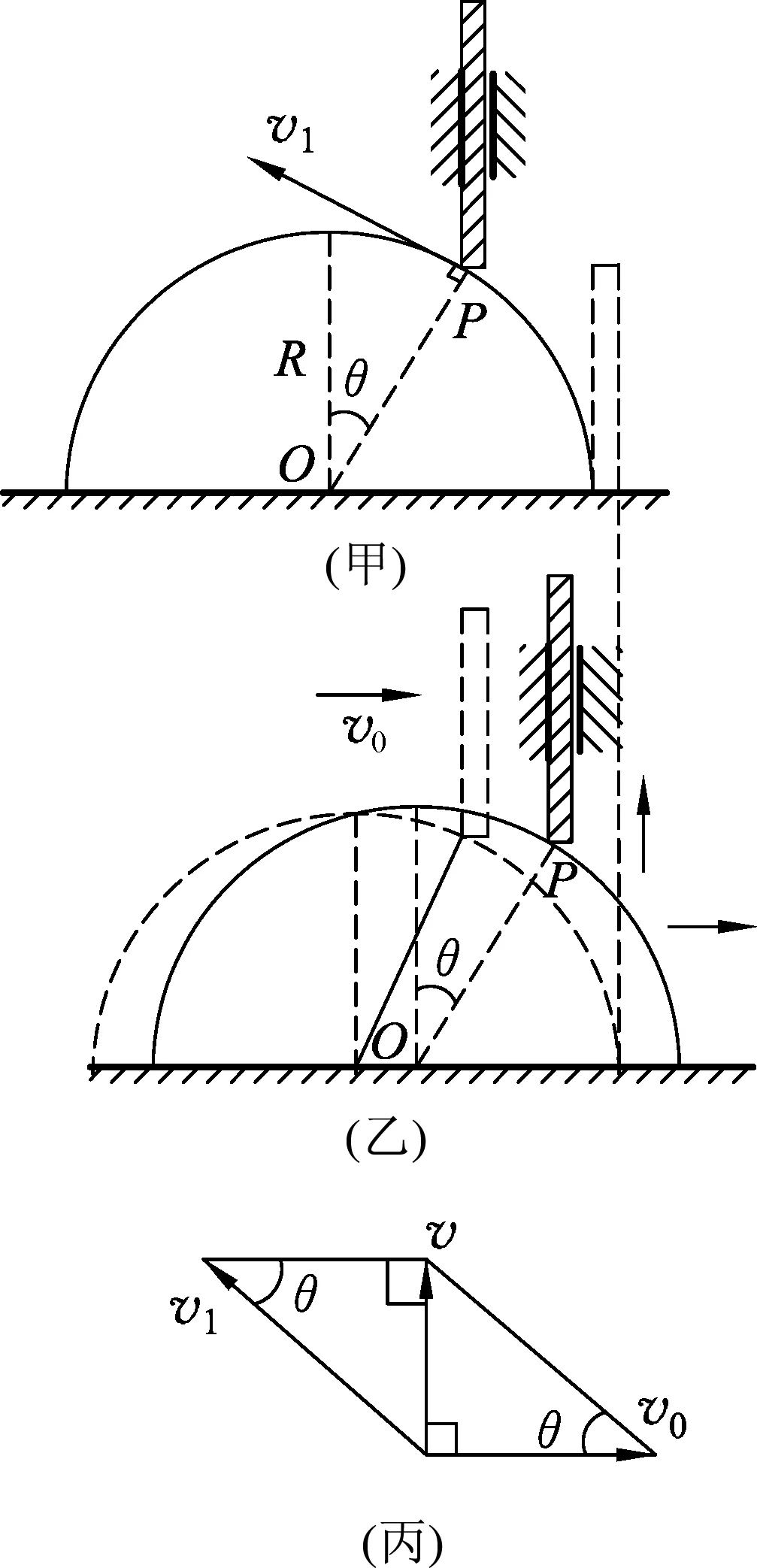
图8
练习2.如图9所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面向右以速度v匀速运动至图中虚线位置,运动中始终保持悬线竖直,下列说法正确的是

图9
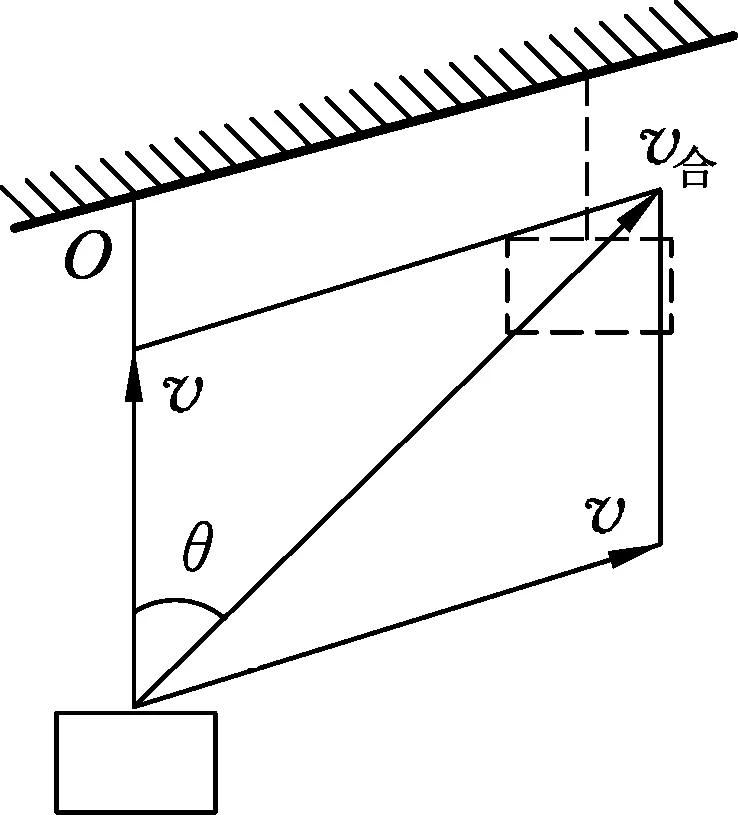
图10
(C) 橡皮的速度与水平方向成60°角.
(D) 橡皮的速度与水平方向成45°角.

上述方法,把一个运动分解为两个简单运动,分别进行研究.学生容易理解,也容易找出分运动的速度.合成时只有一个矢量图,学生容易理解,降低了难度,不防一试.
