例析天津高考压轴题与竞赛题渊源
2019-07-30李鑫
李 鑫
(浙江省桐乡第一中学,浙江 嘉兴 314500)
高考压轴题历来承担着选拔优秀学生的作用,一般物理的压轴题都会在物理建模、物理情景复杂程度以及数理逻辑链上增加难度.[1]由于竞赛问题天然具有这样的性质,所以把竞赛问题进行降阶处理,是高考压轴题的一个重要题源.[2]在各种级别的考试中,试题有明显的“自上而下”的流动形态,[3]即在高级别测试的复杂问题经过简化“下放”到低一级考试当中.实际上,历年物理竞赛决赛题或复赛题,就有科研一线实际问题的简化降阶,在美国AP和SAT测试中,[4]这样的现象亦屡见不鲜.
2004年以来,天津物理试题开始自主命题.天津卷一直坚持自己理念,辨识度高,尤其在最后一题选择上颇多亮点.历年天津卷压轴题,有高级物理技巧的要求、有现实模型的建立、也有深刻物理原理的追问.这些试题不少来源于各级别竞赛试题,本文遴选4道真题并追本溯源,找到各自题源做对比,首先进行分类,然后讲述试题演化历程,评析试题物理内涵和选拔功效,最后提出竞赛和高考的一些联系,以及师生应对的策略.
1 2015年天津高考压轴题与“正则动量”
1.1 原题展现
现代科学仪器常利用电场、磁场控制带电粒子的运动,如图1,真空中存在着如图1所示的多层紧密相邻的匀强电场和匀强磁场,电场与磁场的宽度均为d,电场强度为E,方向水平向右;磁感应强度为B,方向垂直纸面向里.电场、磁场的边界互相平行且与电场方向垂直.一个质量为m、电荷量为q的带正电粒子在第1层电场左侧边界某处由静止释放,粒子始终在电场、磁场中运动,不计粒子重力及运动时的电磁辐射.
(1) 求粒子在第2层磁场中运动时速度v2的大小与轨迹半径r2;
(2) 粒子从第n层磁场右侧边界穿出时,速度的方向与水平方向的夹角为θn,试求sinθn;
(3) 若粒子恰好不能从第n层磁场右侧边界穿出,试问在其他条件不变的情况下,也进入第n层磁场,但比荷较该粒子大的粒子能否穿出该层磁场右侧边界,请简要推理说明之.
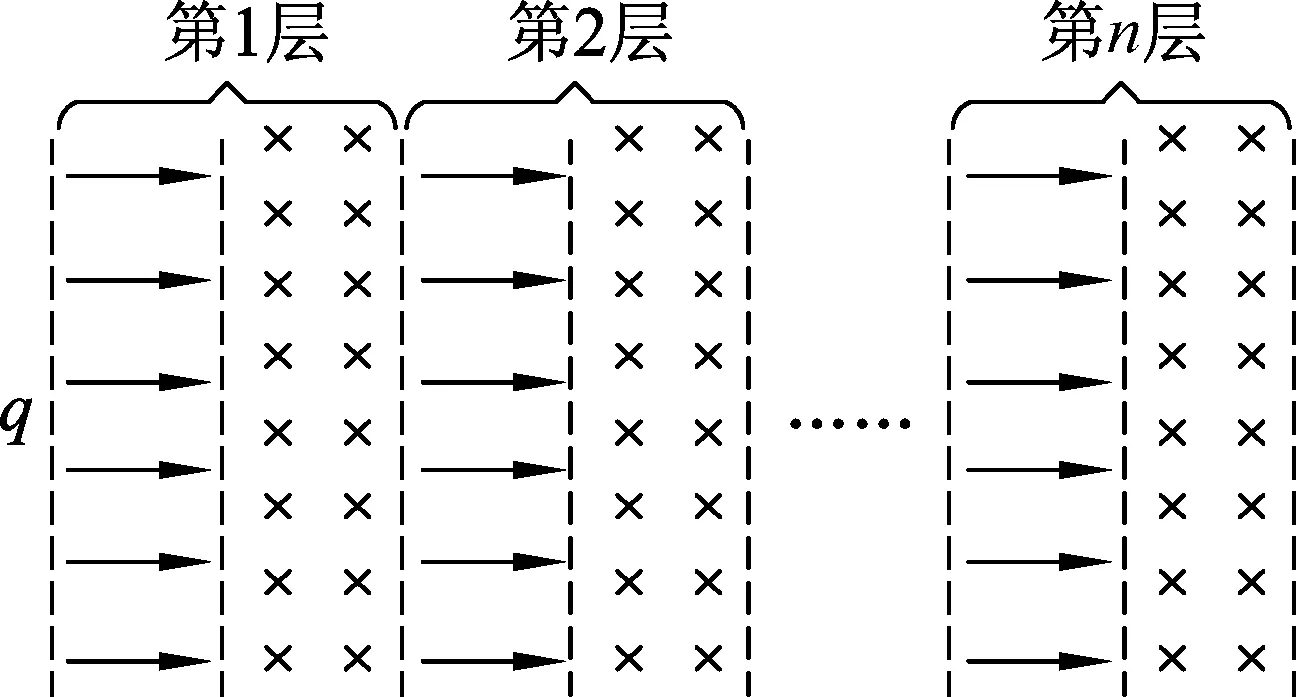
图1
1.2 高考角度
天津历年压轴题设问方式非常统一,一般都是3个小问,3个设问很注重梯度性,第一问是送分问题,照顾绝大数学生,第二问是此题精华,最具区分度,第三问是基于第二问的定性讨论,很考验物理思维.下面的例子也会充分体现这个规律.
在高考物理试题中,一般数学处理技巧难度不大,试题更加侧重于学生对物理情景的认知和物理过程的建立.本题第二问首先需要学生对于粒子在多层电磁场中的运动轨迹有清晰的把握,然后能根据物理关系和几何关系建立递归关系,难点集中在递归关系建立上,即便对于高中的数列压轴题中,递归数列的问题也是一个难点.所以本问不仅物理情景复杂,数学关系的构建更难.

图2
解析:如图2所示,粒子进入第n层磁场时,速度的方向与水平方向的夹角为αn,从第n层磁场右侧边界穿出时速度方向与水平方向的夹角为θn,粒子在电场中运动时,垂直于电场线方向的速度分量不变.
设粒子在第n层磁场中运动的速度为vn,轨迹半径为rn(下标表示粒子所在层数),有
(1)
(2)
vn-1sinθn-1=vnsinαn.
(3)
由图2根据几何关系可以得到
rnsinθn-rnsinαn=d.
(4)
联立可得
rnsinθn-rn-1sinαn-1=d.
(5)
由此可看出r1sinθ1,r2sinθ2,…,rnsinθn为一等差数列,公差为d,可得
rnsinθn=r1sinθ1+(n-1)d.
(6)
当n=1时:
r1sinθ1=d.
(7)
联立可解得
(8)
1.3 竞赛角度
带电粒子仅受洛伦兹力情况下,水平方向速度对应的洛伦兹力在竖直方向上,利用动量定理,有
qvxBdt=d(mvy),
积分得
qBx=mvy.
(9)
所以粒子在磁场中在竖直方向获得的速度是由粒子在磁场中水平方向位移所决定的.
经历n个区域电场加速
(10)
qvxBdt=d(mvy).
(11)
经历n个磁场区域偏转,得
qBnd=mvy.
(12)
即
(13)
1.4 对比分析
第1种解法需要学生有耐心分析物理过程的能力,还要有出色的数学处理能力,至少是要具备构建并求解等比数列和分析几何图形的能力,如果学生都按照这些要求得出正确答案,选拔出来的学生无疑是极为出色的.第2种解法体现出很大优越性.对于竞赛生来说,[5]这道题就是一个结论题,掌握熟练的学生甚至可以在考场上秒杀这道题.
2 两种模型,不同降阶
2016年和2013年天津压轴题背景都是经典模型,这两个模型都源自竞赛问题,天津卷对此做了截然不同的降阶处理方式.
2.1 “磁阻尼”问题题源对比
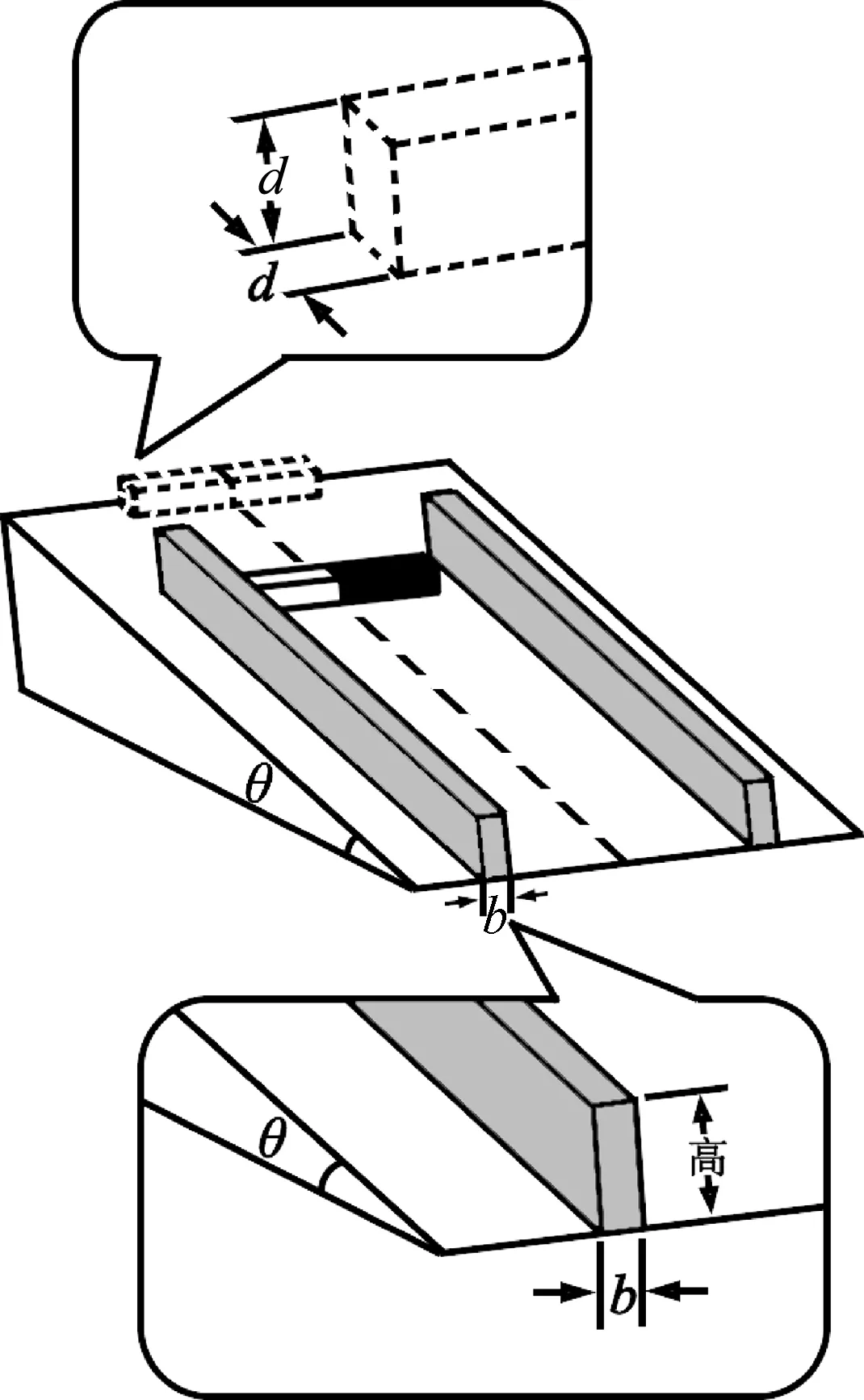
图3
原题.(2016年天津高考题)电磁缓速器是应用于车辆上以提高运行安全性的辅助制动装置,其工作原理是利用电磁阻尼作用减缓车辆的速度.电磁阻尼作用可以借助如下模型讨论:如图3所示,将形状相同的两根平行且足够长的铝条固定在光滑斜面上,斜面与水平方向夹角为θ.一质量为m的条形磁铁滑入两铝条间,恰好匀速穿过,穿过时磁铁两端面与两铝条的间距始终保持恒定,其引起电磁感应的效果与磁铁不动、铝条相对磁铁运动相同.磁铁端面是边长为d的正方形,由于磁铁距离铝条很近,磁铁端面正对两铝条区域的磁场均可视为匀强磁场,磁感应强度为B,铝条的高度大于d,电阻率为ρ.为研究问题方便,铝条中只考虑与磁铁正对部分的电阻和磁场,其他部分电阻和磁场可忽略不计,假设磁铁进入铝条间以后,减少的机械能完全转化为铝条的内能,重力加速度为g.
(1) 求铝条中与磁铁正对部分的电流I;
(2) 若两铝条的宽度均为b,推导磁铁匀速穿过铝条间时速度v的表达式;
(3) 在其他条件不变的情况下,仅将两铝条更换为宽度b′>b的铝条,磁铁仍以速度v进入铝条间,试简要分析说明磁铁在铝条间运动时的加速度和速度如何变化.
(第6届亚赛题)[6]当一磁铁在靠近非磁性导体如铜和铝旁边运动时,磁铁将会受到耗散力的作用,运动将减缓甚至停止,这一效应称为磁刹车效应.在物理演示实验室中,常常表演这一效应.实验表明,磁刹车力依赖于磁铁的磁矩、非磁性导体的电导、磁铁和导体的尺寸和形状、磁铁到导体表面的距离和磁铁相对导体的运动速度.磁刹车力满足如下经验关系
FMB=-k0dpvn,
式中k0是一常数,与磁矩、导体的电导和导体及磁体的几何形状有关,d为磁铁中心到导体表面的距离,v为磁铁的运动速度.实验仪器:圆环形的钕铁硼磁铁,厚度tM=(6.3 ±0.1) mm,外环直径dM=(25.4 ±0. 1) mm, 质量m=(21.5 ±0.5) g.磁极在两侧面上.另有2根铝条,塑料支架,数字秒表, 直尺,倾斜放置的有机玻璃板,板上有一直线的轨道供磁铁在其上运动.
实验方法和问题:
(1) 让磁铁沿斜面上的轨道向下滚动,注意斜面的倾斜角要选择适当,不要让磁铁滚动太快,当磁铁的磁场很强时,由于地磁场作用,磁铁会受到显著的力矩作用,使得磁铁滚动时发生扭转而与轨道发生摩擦,如何摆放实验装置才能使得这一力矩最小?并作图表示.
(2) 如图4所示,将2条铝条放置在斜面轨道两边,图中d=5 mm.再次让磁铁在轨道上运动,磁铁的滚动因为磁刹车效应而比没有铝条时缓慢得多.画出磁感应线分布图以及铝条和磁铁的受力图,解释磁刹车机理.

图4
(3) 研究磁刹车力与幂指数p和n的关系.实验装置如图4所示,磁铁与导体间d=5 mm(磁铁与两侧导体表面间距约为2 mm).
① 保持间距d不变,研究磁刹车力与速度的关系.确定式(1)中速度幂指数n的大小.
② 对称地移动磁铁两侧的铝条以改变导体到磁铁的间距d,研究磁刹车力与磁铁与导体间 距d的依赖关系.确定方程(1)中间距d的幂指数.
毫无疑问,两道题同出一源.
无论是亚赛题还是天津题,这个物理模型其实不难定性理解,磁铁在下滑过程中,在正对铝条上会产生涡流,于是会对磁铁有阻碍,但是如何从定性分析转换到定量求解,两道题都做了不同程度的精彩演绎,亚赛题是把它设计成一道实验题,用到的模型自然就是涡流的模型.
(14)
回路中的电阻为R,则消耗的电功率
(15)
则磁铁所受的阻力为
(16)
即只要磁铁和铝棒之间的距离保持不变,那么磁刹车力的大小与磁铁速度成正比.[7]
有了以上对学生理论分析能力的要求,本题自然就可以设计出第3问,探究磁刹力和速度以及其他影响因素的关系,本题是一道实验题,完美地把理论分析和实验探究融合起来,非常漂亮.
高考题处理模型方式完全不同,立足点是遴选出高考要求下优秀的学生,试题不能大幅度超纲,所以定量分析涡流模型是不行的,于是做了非常巧妙的设定.(1) 只有正对磁铁部分的铝块有磁场,(2) 只有正对磁场部分的铝块有电阻,这两个设定很精彩的对原模型做了降阶处理,把涡流模型变成了动磁场下的切割模型,铝块相对于磁铁向上运动,正对部分铝块相当于是电源,既有电动势也有内阻,而且内阻就是全部电阻.经过这样的设定,就可以转换成高考生可以解决的问题,匀强磁场中导体棒相对运动问题是一个经典话题,可以起到充分选拔作用.
高考题第(2)问求解.
磁铁穿过铝条时,在铝条中产生的感应电动势有
E=Bdv.
(17)
铝条与磁铁正对部分的电阻为R,由电阻定律有
(18)
由欧姆定律有
(19)
联立上式可得
(20)
2.2 “超导”问题题源对比
2.2.1 题源介绍
天津高考和竞赛渊源另一个经典例子是2013年压轴题,此题关注的是超导模型,超导体自诞生以来一直都是热门话题,此题的题源有两个:分别出自第25届复赛和第16届复赛.[8]限于篇幅,这里对比第25届和天津2013年压轴题.
2.2.2 原题展现
(第25届复赛题)零电阻是超导体的一个基本特征,但在确认这一事实时受到实验测量精确度的限制.为克服这一困难,最著名的实验是长时间监测浸泡在液态氦(温度T=4.2 K)中处于超导态的用铅丝做成的单匝线圈(超导转换温度TC=7.19 K)中电流的变化.设铅丝粗细均匀,初始时通有I=100 A的电流,电流检测仪器的精度为ΔI=1.0 mA,在持续一年的时间内电流检测仪器没有测量到电流的变化.根据这个实验,试估算对超导态铅的电阻率为0的结论认定的上限为多大.设铅中参与导电的电子数密度n=8.00×1020m3,已知电子质量m=9.11×10-31kg,基本电荷e=1.60×10-19C.(采用的估算方法必须利用本题所给出的有关数据)
(2013年天津高考题)超导现象是20世纪人类重大发现之一,日前我国己研制出世界传输电流最大的高温超导电缆并成功示范运行.
(1) 超导体在温度特别低时电阻可以降到几乎为0,这种性质可以通过实验研究.将一个闭合超导金属圈环水平放置在匀强磁场中,磁感线垂直于圈环平面向上,逐渐降低温度使环发生由正常态到超导态的转变后突然撤去磁场,若此后环中的电流不随时间变化,则表明其电阻为0.请指出自上往下看环中电流方向,并说明理由.
(2) 为探究该圆环在超导状态的电阻率上限ρ,研究人员测得撤去磁场后环中电流为I,并经一年以上的时间t未检测出电流变化.实际上仪器只能检测出大于ΔI的电流变化,其中ΔI≪I,当电流的变化小于ΔI时,仪器检测不出电流的变化,研究人员便认为电流没有变化.设环的横截面积为S,环中定向移动电子的平均速率为v,电子质量为m、电荷量为e.试用上述给出的各物理量,推导出ρ的表达式.
(3) 若仍使用上述测量仪器,实验持续时间依旧为t,为使实验获得的该圆环在超导状态的电阻率上限ρ的准确程度更高,请提出你的建议,并简要说明实现方法.
2.2.3 对比分析
和上一题不同,这道“超导”的问题高考题完全脱胎于第25届的复赛题,并没有做“模型”认知上的降阶.只做了两点变化,其一是设了3个小问,让学生有分可拿,其二是把原题的具体数值舍去,降低了数值计算的要求,当然,抛却了具体数值也降低了题目设计上的难度,避免了科学性错误.对于学生,建模难度也会下降,因为不会受到数值的干扰,全部注意力都在物理量上,高考题比复赛题设问指向性更明显,复赛题的建模含义有些模糊,需要学生判断清楚.
细致分析高考题设问,试题没有体现出分层设问的特点,第1问是送分问题,并没有为第2问做铺垫,第2问是此题核心一问.这种设问方式和过去高考压轴题只有一问的方式没有本质区别,因为题目设计者并没有充分搭设桥梁,为学生建模开拓思维.笔者以为此题做为高考题实在太难了,这可是物理竞赛的复赛试题,对于学生物理素养提出极高要求,而且中间还涉及到电流微观表达式和小量计算,需要学生对高中物理知识的本源有非常透彻的了解.下面是高考题第(2)问求解过程.
设圆环周长为l、电阻为R,由电阻定律得
(21)
设t时间内环中电流释放焦耳热而损失的能量为ΔE,由焦耳定律得
ΔE=I2Rt.
(22)
设环中单位体积内定向移动电子数为n,则
I=nevS,
(23)
式中n、e、S不变,只有定向移动电子的平均速率的变化才会引起环中电流的变化,电流变化大小取ΔI时,相应定向移动电子的平均速率的变化得大小为Δv,则
ΔI=neSΔv.
(24)
设环中定向移动电子减少的动能总和为ΔEk,则
(25)
由于ΔI≪I,可得
(26)
根据能量守恒定律
ΔE=ΔEk.
(27)
联立上述各式,得
(28)
t=365×24×3600 s=3.15×107s.
ρ=1.4×10-26Ω·m.
所以电阻率为0的结论在这一实验中只能认定到ρ≤1.4×10-26Ω·m.
2.3 小结
对比2013年和2016年天津高考压轴题,共同之处都是来源于竞赛的物理模型,但是2013年的压轴题没有经过什么“降阶”处理,几乎是照搬竞赛原题,或许是前车之鉴,2016年天津压轴题的设计要精彩得多,把看似高考考生没办法解决的问题通过两点假设约定变成了可以解决的问题,是一个经典的从竞赛到高考的好问题.
3 “磁悬浮”列车问题的“前世今生”
天津高考压轴题和竞赛最经典例子还要数2008年的高考压轴题,此题也可以说是天津高考压轴和竞赛的渊薮,[9]试题的背景是当时很热的磁悬浮列车,题源是第23届全国中学生物理竞赛复赛的第5题,第23届考试时间是2006年,2007年上海的最后一题就是承接此题,2008年天津压轴题可以视作一脉相承,下面就来比较这3道题.
3.1 试题对比
(第23届复赛题)磁悬浮列车是一种高速运载工具.它具有两个重要系统.一是悬浮系统,利用磁力(可由超导电磁铁提供)使车体在导轨上悬浮起来与轨道脱离接触.另一是驱动系统,在沿轨道上安装的三相绕组(线圈)中,通上三相交变电流,产生随时间、空间作周期性变化的磁场,磁场与固连在车体下端的感应金属板相互作用,使车体获得牵引力.
为了有助于了解磁悬浮列车的牵引力的来由,我们求解下面的问题.
设有一与轨道平面垂直的磁场,磁感应强度B随时间t和空间位置x变化规律为B(x,t)=B0cos(ωt-kx)式中B0、ω、k均为已知常量,坐标轴x与轨道平行.在任一时刻t,轨道平面上磁场沿x方向的分布是不均匀的,如图5所示.图中Oxy平面代表轨道平面,“×”表示磁场的方向垂直Oxy平面指向纸里,“·”表示磁场的方向垂直Oxy平面指向纸外.规定指向纸外时B取正值.“×”和“·”的疏密程度表示沿着x轴B的大小分布.一与轨道平面平行的具有一定质量的金属矩形框MNPQ处在该磁场中,已知与轨道垂直的金属框边MN的长度为l,与轨道平行的金属框边MQ的长度为d,金属框的电阻为R,不计金属框的电感.
(1) 试求在时刻t,当金属框的MN边位于x处时磁场作用于金属框的安培力,设此时刻金属框沿x轴正方向移动的速度为v.
(2) 试讨论安培力的大小与金属框几何尺寸的关系.

图5
(2007年上海高考题)如图6(a)所示,光滑的平行长直金属导轨置于水平面内,间距为L、导轨左端接有阻值为R的电阻,质量为m的导体棒垂直跨接在导轨上.导轨和导体棒的电阻均不计,且接触良好.在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为B.开始时,导体棒静止于磁场区域的右端,当磁场以速度v1匀速向右移动时,导体棒随之开始运动,同时受到水平向左、大小为f的恒定阻力,并很快达到恒定速度,此时导体棒仍处于磁场区域内.

图6
(1) 求导体棒所达到的恒定速度v2;
(2) 为使导体棒能随磁场运动,阻力最大不能超过多少?
(3) 导体棒以恒定速度运动时,单位时间内克服阻力所做的功和电路中消耗的电功率各为多大?
(4) 若t=0时磁场由静止开始水平向右做匀加速直线运动,经过较短时间后,导体棒也做匀加速直线运动,其v-t关系如图6(b),已知在时刻t导体棒瞬时速度大小为vt,求导体棒做匀加速直线运动时的加速度大小.
(2008年天津高考题)磁悬浮列车是一种高速低耗的新型交通工具,它的驱动系统简化为如下模型,固定在列车下端的动力绕组可视为一个矩形纯电阻金属框,电阻为R,金属框置于xOy平面内,长边MN为l平行于y轴,宽为d的NP边平行于x轴,如图7(a)所示.列车轨道沿Ox方向,轨道区域内存在垂直于金属框平面的磁场,磁感应强度B沿Ox方向按正弦规律分布,其空间周期为λ,最大值为B0,如图7所示,金属框同一长边上各处的磁感应强度相同,整个磁场以速度v0沿Ox方向匀速平移.设在短暂时间内,MN、PQ边所在位置的磁感应强度随时间的变化可以忽略,并忽略一切阻力.列车在驱动系统作用下沿Ox方向加速行驶,某时刻速度为v(v (1) 简要叙述列车运行中获得驱动力的原理; (2) 为使列车获得最大驱动力,写出MN、PQ边应处于磁场中的什么位置及λ与d之间应满足的关系式; (3) 计算在满足第(2)问的条件下列车速度为v时驱动力的大小. 图7 显然上面3道题是一脉相承的,3道题目最本源的区别在于对磁悬浮列车驱动电机建模,深圳大学编拟的竞赛题采用的是真实物理情景,而天津高考题和上海高考题都做了不同程度的简化.上海高考题简化程度更大些,而天津高考题的磁场随空间还是交变的,难度相应也较大. 评断一道试题的编拟好坏可以看一看跟随者的脚步,在往后的各地市模拟题中,关于磁场和导体棒相对运动的问题基本上都假定磁场是匀强磁场,从这个角度来说,上海试题的处理更近地气一些.但是笔者认为上海的模型过于简约了.天津卷第2问为了降低难度,提醒学生关注金属框和磁场的相对运动问题,第3问则对学生理解感生电动势提出了更本质的追问,需要分析清楚磁通量变化量,本题对于物理知识迁移和实际情景把握更加真实有力. 当然此题更大价值在于引发电磁感应试题一场“小革命”,此后,磁场和导体相对运动模型、关于磁悬浮列车诸种问题如雨后春笋般出现,而且各设问角度,如相对速度、安培力电功率等都来源于这3道题,[10]可以算是一大类问题的渊薮.限于篇幅,关于这3道题目详细解析可以参见《中学物理原创题集》中关于这三道题目的文章.[11] 天津高考压轴题设问方式有如下特征: (1) 问面向全体学生的基础问题,比较容易拿分; (2) 问全题核心一问,难度大,对学生建立物理模型或者数理过程分析能力提出高要求;(3) 问基于第二问发散的问题,通常是定性半定量问题. 通过前文对比分析,天津压轴题来源于竞赛的问题通常是3类,即来源于数理技巧问题、实际物理模型、物理本质追问,关于物理模型处理方式又可以进一步分类: (1) 数理技巧应用(2013、2015年压轴题)二阶小量计算、正则动量应用; (2) 实际物理模型(2008年压轴题)磁悬浮列车模型; (3) 实验室模型(2016年压轴题)磁阻尼模型降阶成相对运动切割模型; (4) 物理本质问题(2013年压轴题) 超导模型、把握能量守恒本质. 从竞赛到高考是一个历久弥新的话题,教师经常在高考压轴题复习时,对如何挑选试题源挑选的困惑.本文指出从竞赛题里寻觅灵感是一个不错的选择,[12]不妨从物理模型、物理本质和数理技巧3个层面进行分类,注重试题演化过程,尤其是竞赛题、高考题和模拟题之间的关联,这样系统的梳理有助于学生把握试题的动向和提升建模分析物理情景的能力.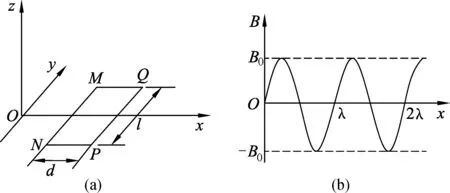
3.2 分析
4 总结
