“拉船”问题通透看

吴珍发

(福建莆田第十中学,福建 莆田 351146)

1 问题的提出

图1

如图1,绳子拉船从A运动到B按运动的合成与分解可以看成是先把船沿着以滑轮为中心的从A转到C,再把船沿绳子方向从C拉到B两个运动的合运动;或者把绳子拉船从A运动到B看成先把船沿绳子方向的从A拉到D,再把船沿以滑轮为中心从D转到B的两个运动的合成．其中合运动和分运动之间的速度关系为v转=v船sinθ,v绳=v船cosθ．

依教材这样的分析对高一的学生还是算有点儿突然但也很巧妙,但是理解起来总的还是觉得有些陌生．对高一的学生,我们不妨另辟蹊径,从其他角度入手,以加强对拉船问题的全面和透彻地理解．

2 横岭侧峰多角度通透看“拉船”

图2

2.1 从三角形三个边之间关系粗浅看

初中学生都学过三角形两边和大于第三边两边差小于第三边这个原理,对于刚升入高中的高一学生,我们可以先从他们很熟悉的三角形边间的关系初步入手研究拉船.

如图2,假设船从A运动到B.在△ABC中，有LAB>LOA-LOB,又v船=LAB/Δt,v绳=(LOA-LOB)/Δt,由此,显然有v船>v绳．

这样我们从学生已知的很粗浅的数学知识入手,粗略知道了船速跟绳速之间的大体关系,对此拉船问题有了初步的理解．

2.2 从极限思想精确分析“拉船”

在高中物理学习中极限思想方法很重要,有关的数学知识会逐步学到,而且极限思维在物理里面的应用也很广泛,其实绳拉船各种瞬时速度关系在极限思维方面可以看成是瞬时速度就是指船在无穷小的时间内通过的位移,也就是为绳拉船通过的无穷小的位移和无穷小的时间的比值．现我们由极限的思维入手分析.

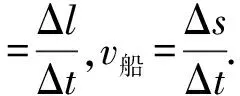
从图中的几何关系可知:

l2=s2+h2.

(1)

(l-Δl)2=(s-Δs)2+h2.

(2)

上两式(1)-(2)并两边同除以Δt,得

当Δt→0时,Δl→0,Δs→0.

由此可得2lv绳=2sv船,

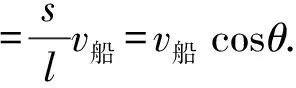
这样分析十分自然,学生由此也加深了对瞬时速度的理解,同时也培养了学生的高中物理学习中极其重要的极限思维思想,从一个崭新的角度加深了对绳子拉船问题的熟悉和精确理解．

2.3 换个角度从功能原理方面看

极限问题比较抽象,我们还可以从我们熟悉的功能关系入手,其实,绳子拉船也是一个利用任何机械都不省功的功的原理问题．

当船水平前进时有

Wf=f·Δs,WF=F·Δl，

又由受力分析可知f=Fcosθ，根据功能原理利用任何机械都不省功,即WF=Wf.可得Δl=Δs·cosθ.两边同除以Δt得

从以上分析可知,无论船水平加速还是匀速都是v绳=v船cosθ．这样我们又从学生很熟悉的物理知识入手解决绳拉船问题,这就犹如桃花源记里面说的,我们的思路经过刚才前面的抽象极限思维如一段狭窄的路段后前面又是一个一马平川的“桃花源”.

2.4 用导数方法彻底解决

其实极限思维也就是大学中学到的导数方法,高中学生后面数学越来越深入也会粗浅学到导数方法．现在我们用导数方法极其简便并彻底解决拉船问题．

如图2,拉船过程中任意时刻,岸高h,定滑轮与船间的绳子长l和船距岸边距离s有如下关系:l2=s2+h2.

显然l和s都是时间的函数,对左右两边对t求导,有2l·l′(t)=2s·s′(t).则

由导数定义可知:s′(t)即为船速,l′(t)即为拉绳速度,因此

即v绳=v船cosθ.

导数作为高等数学的基础,解决此类问题具有初等数学难以企及的优势,但导数知识的方法一般出现在高二下学期的数学课程中,而拉船问题却出现在高一物理中,应注意学生在学完导数都的后续物理学习和复习中点明和使用运用导数,可使学生对此类问题更加深刻理解,获得新的处理物理问题的方法,其实导数方法本质上也是一种极限的思维.这种方法特别对于难度大的比如物理竞赛中应用非常普遍,这也为学生大学的学习打下良好的基础．

3 总结

至此,我们经过多角度的研究,对于拉船问题速度关系的正确答案已经确定无疑,如此经过几种方法多角度的探究,我们拉船问题可以说是已经理解通透．其实,绳子拉船问题高考也常有涉及,比如全国卷或者福建卷好几年都有出现．学生经过如此另辟蹊径从各个角度透彻理解加深印象,特别是对数学里面导数方法应用,在物理竞赛和其他物理问题经常有用到,有时候解题犹如战场的轻骑兵,很快就可以解决问题．当然对于大部分的高中绳子拉船问题解题时还是应该多多运用运动的合成和分解方法或者功的原理方法进行解题,这样的解答方法在普通解题过程中比较常用,特别是这样的解法物理过程明白物理分析味道浓厚,较为普遍得到师生的青睐和推崇．