迈克尔逊干涉圆环中心点漂移对波长测量结果的影响分析

魏茂金 张武威 杨秀珍

(1. 装备智能控制福建省高校重点实验室, 福建 三明 365004; 2. 三明学院机电工程学院,福建 三明 365004)

迈克尔逊干涉仪是利用分振幅法实现薄膜干涉的精密仪器,对物理学和计量学发展产生重大的影响．利用迈克尔逊干涉仪可观察到等倾干涉条纹、等厚干涉条纹以及白光的干涉现象,在科学研究与工程实践中具有重要的实际意义与应用价值．[1-4]在大学物理实验中,常用它来测量钠光和He-Ne激光器波长．在实验过程中,圆环中心漂移是很常见的现象,然而文献很少涉及圆环中心漂移问题,本文将利用几何学与光学知识,从理论上分析动镜M1移动过程中干涉圆环中心发生漂移的原因,设计实验方案,探究圆环中心位置漂移对波长测量精度的影响．

1 迈克尔逊干涉仪测波长的原理

1.1 迈克尔逊干涉仪的原理

图1 迈克尔逊干涉仪光路图

迈克尔逊干涉仪的光路如图1所示．[1]G1为分光板,G2为补偿板,M1为可移动反射镜,M2为固定反射镜,M2′为M2在半反射膜的虚像．当M1和M2垂直时,可看到等倾干涉图样,调节M1位置,可看到干涉圆环中心的吞吐现象．

若M1移动Δd,干涉圆环中心条纹涌出或陷入级数Δk,则[5]

(1)

利用上式,可测入射光波长．

1.2 M1与M2′存在夹角时干涉条纹形状

当M1与M2′存在夹角时,将产生等厚干涉条纹．由光程差公式

δ=2nhcosi.

(2)

微分方程为

∂δ=-2nhsini∂i+2ncosi∂h.

对于同一级条纹,由于∂δ=0,则

-hsini∂i+cosi∂h=0.

(3)

从(2)式可以看出:对同一级条纹,入射光倾角增大,必须增大厚度．[5]如图2(a)所示,相较而言,等厚线上P1点的倾角比P2点小,因此干涉条纹就偏离到了更厚的点P2′上,所以看到的干涉条纹变成了一条条的曲线．在图2(b)中的一条条平行直线是十分严格的等厚线,图中的同心圆环是M1和M2严格垂直时的等倾干涉线．图2(b)中P1、P2′、P3′、P4′各点的光程差δ相同,都是在同一根干涉条纹上．从(3)式中还可以看出,相同倾角变化∂i,h越大或sini越大,∂i对光程差δ的影响也就越大．因此,干涉条纹对等厚线的偏离也就更加的显著．所以在人眼注视干涉图样时,同一等厚线上因人眼观察的倾角不同,导致人眼所看到的干涉图样不再是一条条明暗相间的直条纹,而是一条条曲线．

图2 干涉对等厚线的偏离

因此,当M1与M2′有一定倾角时,在毛玻璃片中看到的是一条条弯曲的曲线．当动镜M1′与定镜M2之间存在的倾角非常小时,只要通过改变M1与M2′的距离,还是可以看到曲线弯曲成了一个个同心圆环,只要将圆环中心调至视场中心,此时干涉图样与等倾干涉图样看起来并没有太大的差别．

2 迈克尔逊干涉圆环中心位置漂移的理论分析

2.1 圆环中心位置漂移的原因

如图3为迈克尔逊干涉仪等效光路图．当M1与M2′未平行时,设M1与M2′之间的夹角为α．令S为光源经分光板反射的像位置,M1与M2′间距为d,M1移动到M1′的距离为Δd．S经M1所成的像S1,经M2所成的像S2,经M1′后所成的像S1′．即S1、S2、S1′为等效的虚光源．同时,以毛玻璃片所在位置为x轴,并连接S1、S1′作为y轴,建立直角坐标系．

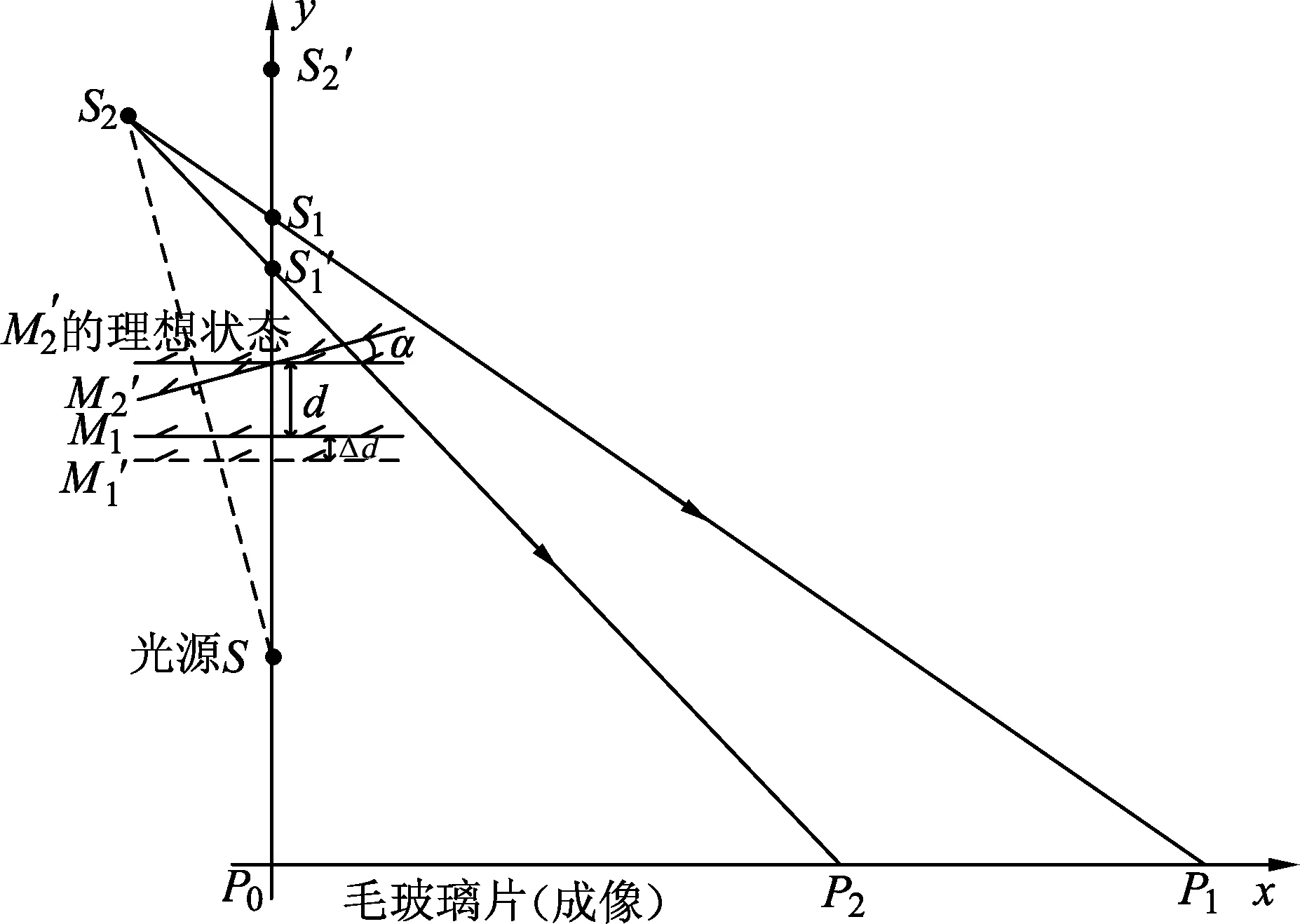
图3 迈克尔逊干涉仪等效光路图

当M1与M2′平行时,假设此时S经M2′(理想状况下)成像于S2′．等效光源S2′、S1在同一直线y轴上,迈克尔逊等倾干涉圆环是以P0为中心的同心圆条纹．此时,M1移动了Δd到达M1′时,光源S成像于S1′,那么虚光源S2′与S1′发生干涉,其干涉图样圆环中心圆环的中心仍在y轴方向P0位置,不会随M1移动而漂移．

当M2′与M1存在一定的夹角时,此时,光源S经M2的像为S2,S2与S1发生干涉时,其干涉圆环中心在S1与S2的连线P1处．当动镜移到M1′时,虚光源S1变为了S1′,S2与S1′发生干涉,干涉圆环中心在S1′与S2的连线P2处,即干涉圆环的中心由P1移动到P2．因此,当M1与M2′不严格平行时,调节M1前后位置,迈克尔逊干涉圆环中心位置会发生漂移,且M1与M2的倾角α越大,圆环中心的漂移量越大．

2.2 圆环中心漂移对波长测量结果的影响

在M1与M2严格垂直时,等倾干涉圆环中心点始终处在y轴方向,不会随M1移动而漂移,M1移动距离Δd时,光程差变化Δδ为

根据干涉条件,可得Δd与干涉圆环中心级数变化Δk的关系为

当M1与M2′存在夹角时,如图3所示,光程的变化量是

显然Δd′≠Δd,此时,采用(1)式将Δd代入得出λ,将会产生较大的测量误差．因此,在实验中干涉圆环的中心位置发生漂移,需要对公式(1)进行修正．

当M1与M2′存在夹角α时,可得修正公式为[6]

(4)

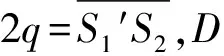
由于在实际操作中,M1也并不是严格垂直于丝杆的轴线．若存在α′夹角,则修正公式为[6]

(5)

3 圆环中心点漂移量对波长测量结果的实验研究

根据以上分析,从理论上可以看出圆环中心漂移对波长测量的存在一定的影响．对此,本文将设计实验方案,在M1起始位置基本相同的情况下,通过微调M1与M2′之间的夹角,测出在动镜M1与M2′之间不同的夹角下圆环中心的偏移量和He-Ne激光的波长,进而探讨干涉同心圆环中心漂移量与波长测量误差之间关系．

3.1 实验内容与方法

如图1迈克尔逊干涉仪,采用He-Ne激光器做光源,调出迈克尔逊干涉圆环,并使干涉圆环圆心调至视场中心,标记干涉圆环中心的位置;通过旋转微调手轮,观察干涉圆环中心每陷入25级后,记下反射镜M1的位置d;当中心圆环数陷入225级时,再次标记干涉圆环中心位置,并使用游标卡尺测量干涉圆环中心的漂移距离X,重复读取3次记录X1、X2、X3,至此完成一次测量．根据上述方法,重新调节迈克尔逊等倾干涉圆环,按上述实验方法进行下一次测量．

为了保证测量的波长值只受到圆环中心点偏移量的影响,在测量的过程中应尽量保证每一次测量时He-Ne激光器的入射角度、M1的起始位置等各个因素都要尽量相同．

3.2 实验数据与结果

3.2.1 实验数据

如表1为调节M1位置与圆环中心漂移量实验数据表,本实验14组数据分别表示M1与M2在不同倾角下,所测量的调节M1位置与圆环中心漂移量．每组实验数据分别测出He-Ne激光干涉图样圆环中心每陷入25级条纹时M1位置d．其中动镜M1的起始位置30.99000 mm,表1中X1、X2、X3分别表示干涉圆环中心陷入225级后,圆环中心的偏移量的3次测量数据．

表1 M1位置与圆环中心漂移量实验数据

对表1数据用逐差法处理,即每隔125圈,计算一次M1的移动距离Δdk，

Δdk=da+125-da.(其中a=0,25,50,75,100)

因此,表1中每组数据经计算,可得到表2中Δd1～Δd5共5组数据．

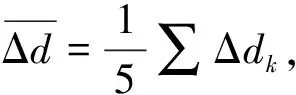
利用式(1),有

由上式可计算求出Ne-He激光波长实验测量值λ,及与标准波长632.8 nm的偏差值Δλ,如表2所示,表中ΔX表示条纹涌出225级后,对干涉同心圆环中心漂移量3次测量之后的平均值．即

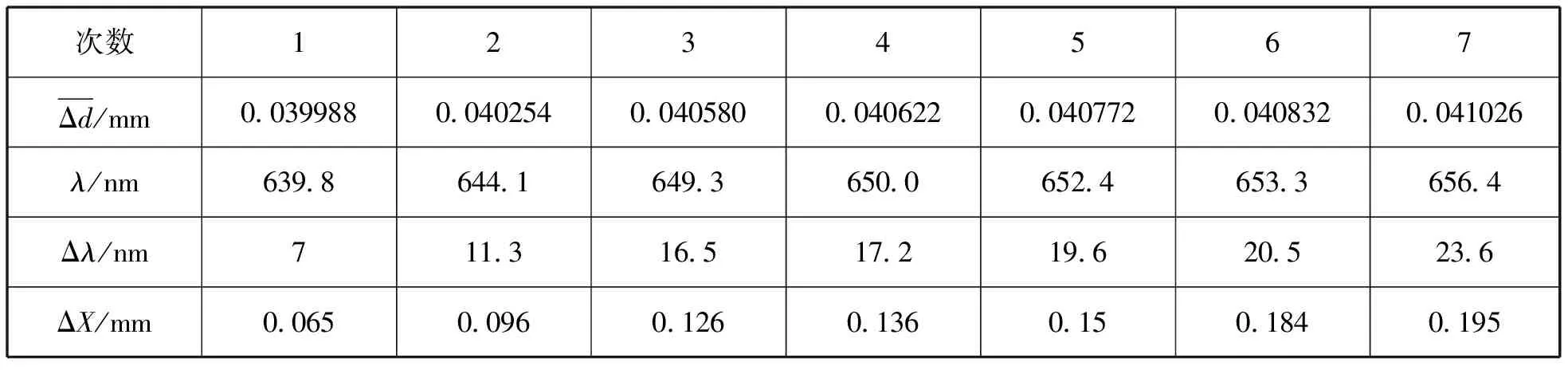
表2 波长与圆环中心漂移量数据计算

由表2数据,以ΔX为横坐标,Δλ为纵坐标,得到干涉图像圆环中心漂移量与λ测量误差的关系曲线,如图4所示．图中的黑点代表原始数据,用实线对原始数据用二次曲线进行拟合．

图4 圆环中心漂移量与波长误差关系

3.2.2 实验结果

从图4不难看出,波长的测量误差与干涉图样同心圆环中心的偏移量总体上呈现出一种正相关的趋势,波长的测量误差大体上随干涉图样同心圆环中心偏移量的增加而逐渐上升,偏移量ΔX越大,λ的测量误差也越大,二者基本呈二次曲线关系．

M1与M2之间的夹角越大,干涉同心圆环中心的漂移量随之增大,波长λ测量误差也进一步加大．此外,还可以利用这一规律来判别M1与M2是否严格的垂直．当M1与M2越接近垂直时,干涉圆环中心的漂移量越小,λ的测量值也就越接近于标准值．因此,为了提高实验的精确性,应前后大幅度的转动粗调节旋钮,对圆环中心的漂移量进行大致的判断,若干涉同心圆环中心的漂移较大,就继续微调M1与M2后的螺丝．如此反复,直到找到一个圆环中心漂移量最小的一个位置,再开始测量波长．这样可以大大减低M1与M2不严格垂直时所带来的实验误差,避免了实验过程中的盲目性,进一步加大了实验的精确性．

4 总结

综上所述,本文主要研究迈克尔逊干涉仪干涉图样同心圆环中心点漂移对波长测量结果的影响,通过对迈克尔逊干涉仪成像的等效光图进行分析,可知当M1与M2未垂直时,干涉圆环中心发生了漂移．M1与M2的倾角越大,干涉同心圆环中心的漂移量ΔX就越大．在M1与M2在未严格垂直的情况下,实验测出He-Ne激光器波长与圆环中心的漂移量,通过对实验数据的分析中可以看出:干涉圆环中心的漂移量越大,波长测量误差也越大,二者基本呈二次曲线正相关关系．此外,利用干涉圆环中心漂移现象,还可判断M1与M2是否严格的垂直,有效地减少了实验过程的盲目性,增加实验的准确性．