静电阵列探测理论与数值模拟方法*

李炜昕，陈若飞，李建伟,赵文龙，周学安

(1 上海无线电设备研究所, 上海 200090； 2 上海市目标识别与环境感知工程技术研究中心， 上海 210090；3 上海机电工程研究所， 上海 200090)

0 引言

随着空中来袭目标的迅速发展，在隐身技术、人工有源干扰，甚至恶劣的电磁环境情况下，基于无线电、激光原理的传统的探测体制存在明显缺陷或不足，甚至无法正常工作，失去作战效能。静电探测就是通过检测目标的静电场而获得目标信息的探测方法，在静电隔墙探测、气固两相流参数测量、航空发动机的状态监测、狙击手方位探测及空中飞行目标的方位探测等领域具有广泛的应用前景[1-2]。

目前，国内外对静电探测数值模拟技术的研究已经相当深入和广泛。Fujiwara等人[3]基于Maxwell电磁场基本理论对地板表面电势进行了建模分析，获取了地板表面电势分布特征。Neil等人采用缩小模型模拟方法，实验测量了F4-J飞机的静电场，初步表明飞机的翼展和尾部有较强的电场，并给出了具体的数值，等效获取了弹目交会过程中环形感应电极的变化曲线。Vinci等人[4]基于有限元方法建立MOM计算模型，分析了近地面和墙面处目标的电场密度分布，获取放大因子与荷电量、脱靶量相关。刘尚合等人[5]建立飞机穿云摩擦起电理论模型，通过数值建模和仿真分析研究了各因素对飞行器带电量和电位的影响。

但是，在可查文献中所进行的研究主要是目标电荷密度分布、静态条件下目标静电场分布等内容，对于弹目交会特性的研究尚不成熟[6-8]。文中基于静电探测和静电场计算基本理论，建立弹目交会有限元数学模型，探讨了感应电极表面电荷变化特征，为静电探测系统的优化设计提供理论支撑。

1 静电探测系统理论模型

静电探测技术是通过检测目标的静电场的变化而获得目标信息的探测方法，由于静电感应在静电探测系统敏感元件的内外侧感应出大小相等、极性相反的静电荷。静电探测系统敏感元件与弹体处于静电场中，相互之间存在耦合电容和泄漏电阻，因此，电荷灵敏等效数学模型如图1所示。静电探测系统对外接口电路可以看作是一个电荷源，输入阻抗由Cp和Rp构成，包括泄露电阻和耦合电容。反馈网络由Rf和Cf组成，实现对电荷信号的放大和阻抗匹配功能。

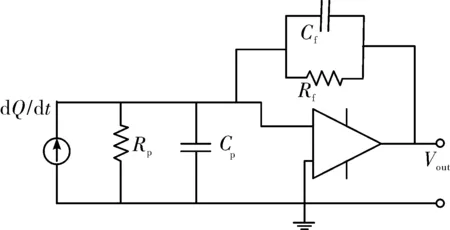
图1 电荷灵敏型理论模型

输出电压与静电探测系统感应电量Q之间关系的复数表达式如下：

(1)

电荷放大器的低频截止频率取决于反馈网络频率，电荷放大器的下限频率为：

fmin=1/(2πRfCf)

(2)

假设t=0表示目标经过坐标位置x=0的时刻，可得到下述表达式:

(3)

探测电极所获取的感应电荷量表达式可简化为：

(4)

基于电荷放大器电路模型，上式可用于计算静电探测系统输出信号。

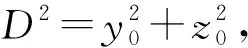
(5)

静电感应电极获取的最大感应电荷量为：

(6)

感应电荷表达式可等效为：

(7)

2 数值计算控制方程

交会过程中携带电荷的离散相与感应电极通过静电感应而达到静电平衡状态形成静电场，可以用Poisson方程和相应的边界条件来描述，其对应的等价变分问题为:

(8)

由于弹目交会过程中空间电荷的分布十分复杂,难以获得三维静电场问题的解析解。因此可采用有限元方法进行数值计算,利用四面体单元对求解场域进行离散化，获得电极上感应电荷的分布情况。

(9)

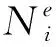
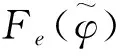
(10)

将式(10)代入式(8),并对φi求导可得:

(11)

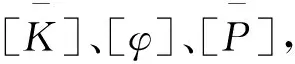
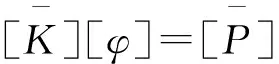
(12)

结合边界条件，求解式(12)可以得到场域内的电场分布，进一步分析就能够求得场强分布和电极上的感应电荷。

3 数值计算结果分析

3.1 有限元模型

由于耦合模型需要进行静态和参数化动态分析，且形状相对复杂，简化为二维模型较困难，故采用三维模型进行电场仿真计算。利用有限元仿真分析软件Maxwell，以某型导弹为研究对象，建立有限元数学计算模型，如图2所示。

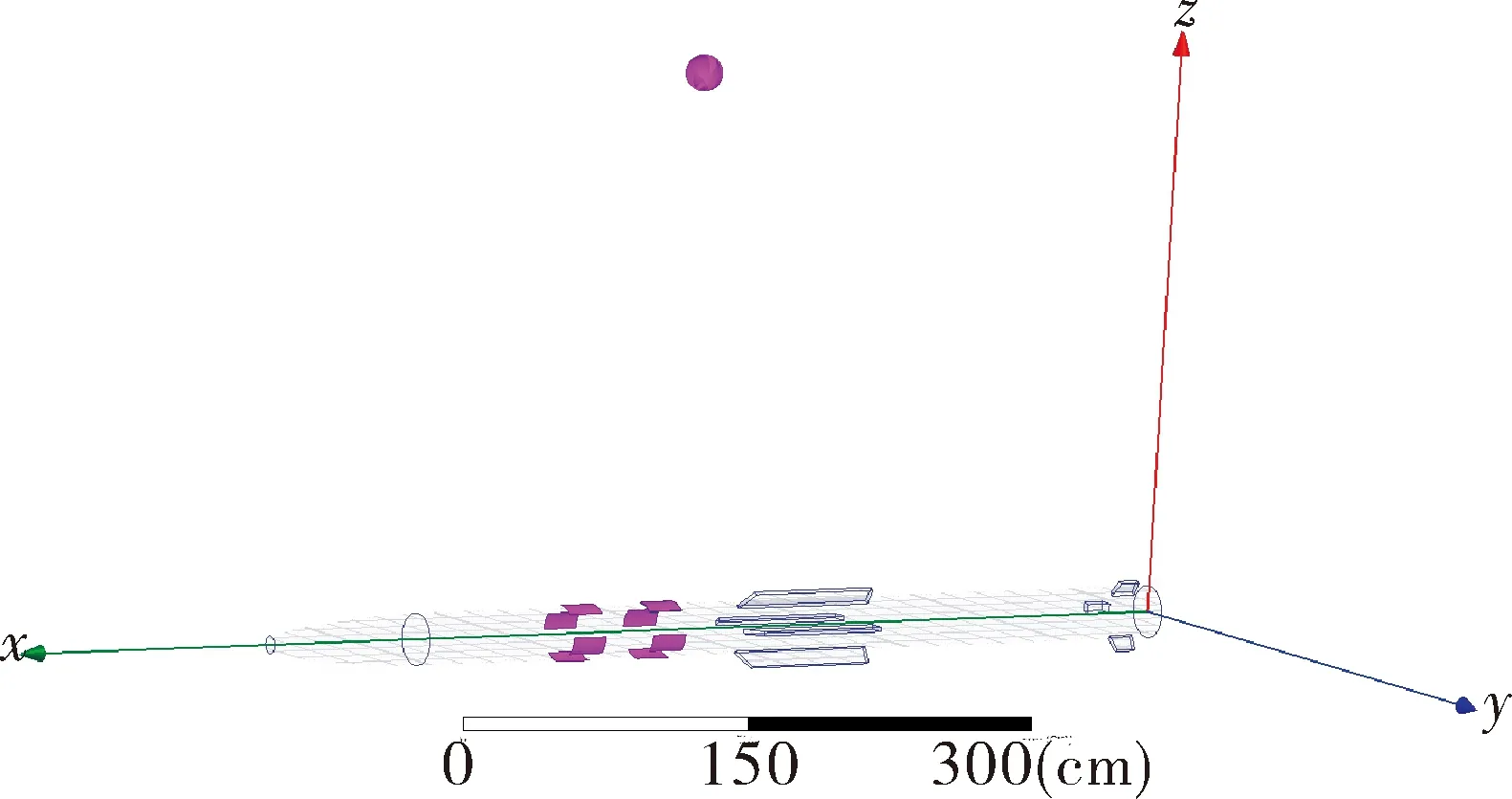
图2 有限元数学计算模型

交会目标为400 mm小球，材料为铝，运动方向为x轴方正向；感应电极由两组片状铜板构成，厚度为1 mm，两组电极间距0.4 m，每组电极呈正交分布；求解域为矩形空气场；感应电极和导弹均设置为悬浮状态。

3.2 目标静电场分布

激励电压为2 kV，在导弹周围无其他带电物体影响条件下，得到导弹模型表面电荷分布情况如图3所示。

图3 导弹表面电荷分布

从仿真结果中可以看出，导弹的头部、舵部、翼部和尾部的感应电荷量相对集中，表面电荷密度较高，而弹身其他地方的表面电荷密度则较低，这种现象主要是由于尖端效应引起的。当导弹尖端越尖时，其曲率就会越大，从而面电荷密度就越高，其附近场强也越强，表面电荷分布在空中呈现较好的对称性。

3.3 探测距离分析

在Maxwell中对弹目交会过程进行参数化建模，利用参数动态扫描功能使导弹感应电极中心与目标做水平交会运动，脱靶量为3 m，交会距离从两者水平距离为-10 m开始到10 m结束。利用Maxwell场计算器中的公式，获得在交会过程中电极体外表面的总电荷量，感应电极表面电荷密度分布如图4所示，感应电极1获取的感应电荷信号如图4所示。

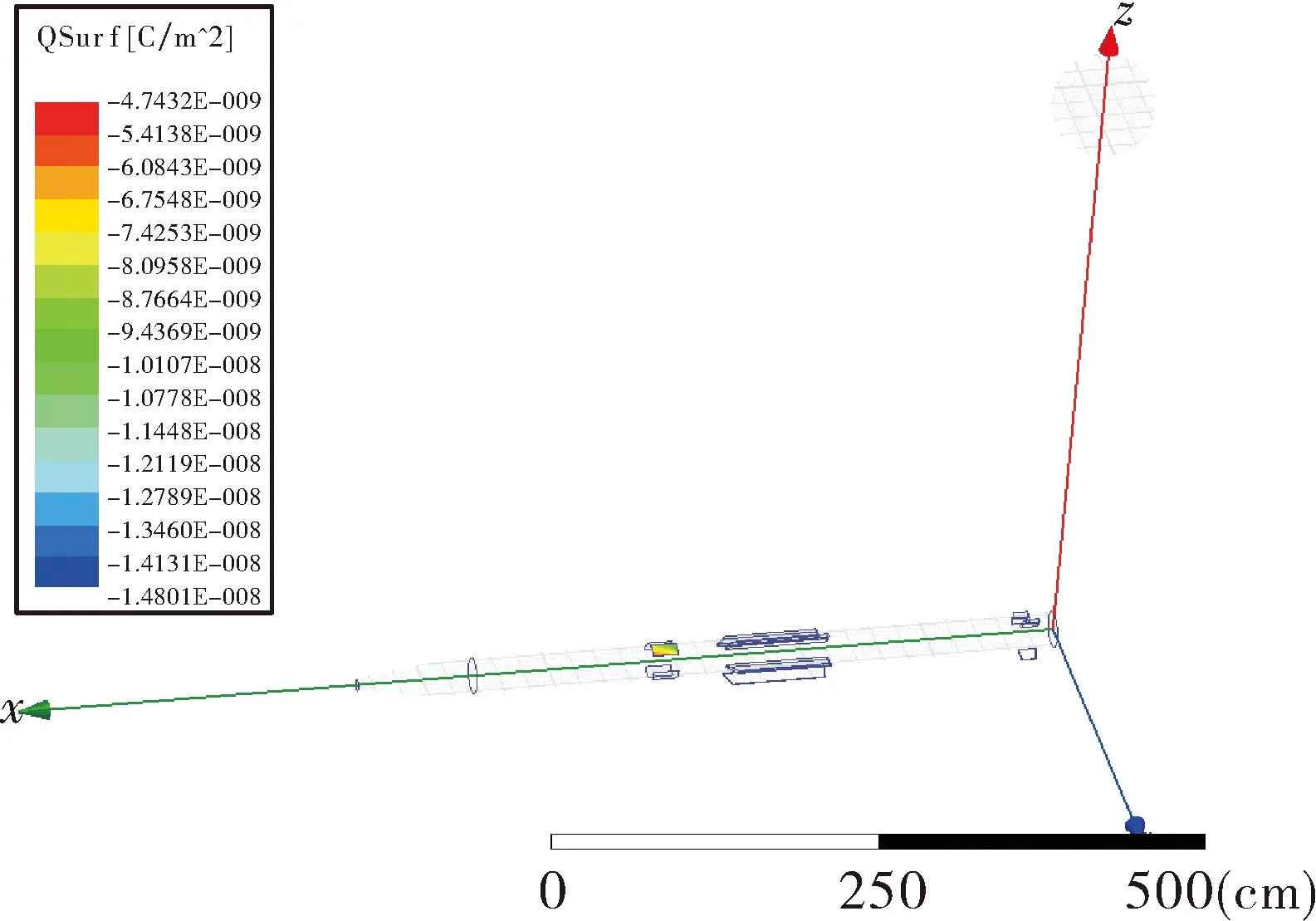
图4 感应电极表面电荷密度

根据图5仿真结果可知，感应电极1电荷量曲线与理论计算趋势一致，在由远及近的交会过程中，感应获取的电荷极性与目标电荷极性相反。电荷总量随着弹目距离的变化而变化，在接近目标过程中电荷总量逐渐增大直到脱靶量时刻的最大值，在远离目标过程中电荷总量逐渐减小直至消失。

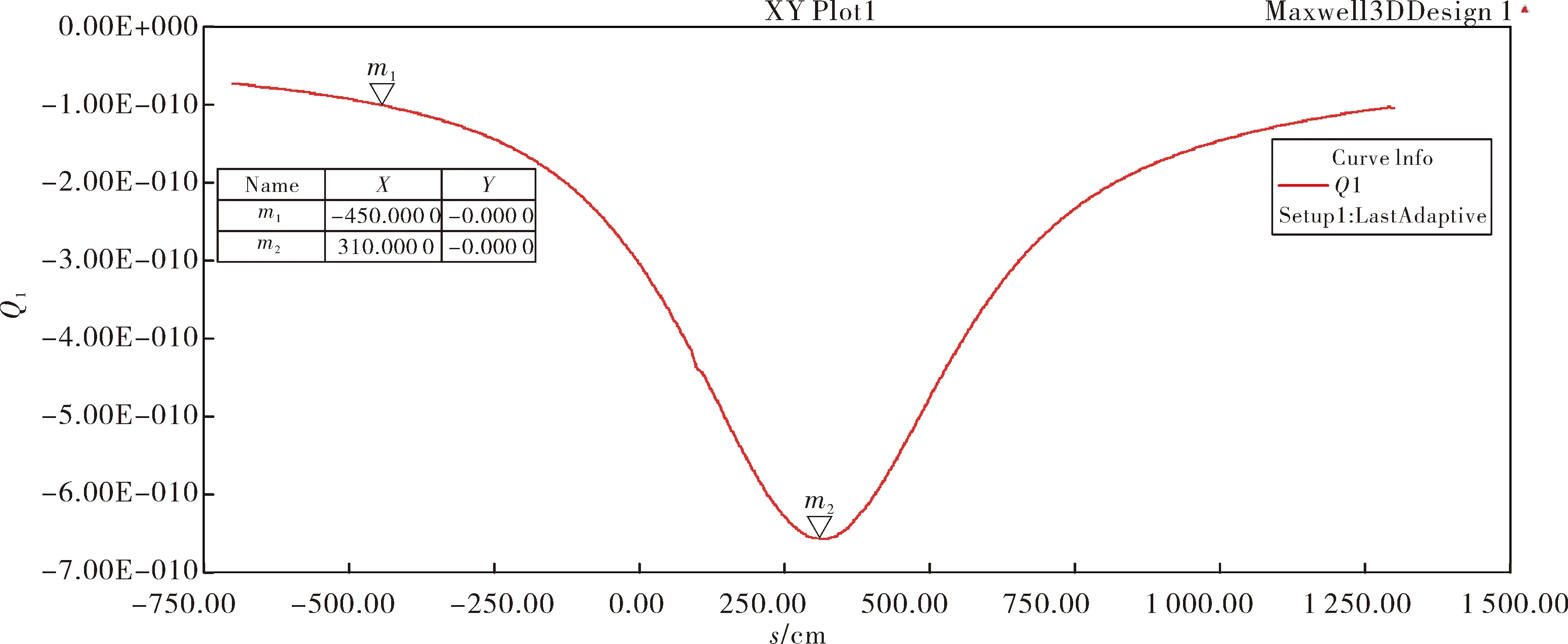
图5 感应电极1获取的电荷量

在感应电荷量变化曲线上分别取2个采样点m1、m2，对应的电荷总量分别为-1E-10 C、-6.8E-10 C。由静电探测基本原理，感应电荷需经过静电探测传感器输出能被信号处理机处理的电压信号，因此静电探测传感器灵敏度成为静电探测系统的关键。调研国内外微弱信号检测水平，美国吉时利、丹麦BK、德国奇石乐以及国内多家传感器公司均拥有pC量级的电荷检测能力。综上分析，在m1位置相对水平距离7.9 m处，即弹目距离为8.45 m时静电探测系统已完全具备探测目标的能力。

3.4 感应电荷分布特性

根据第1节静电目标方位探测理论模型，建立8电极有限元数值仿真分析模型，小球目标在感应电极原点(-3 m，0，3 m)的位置(以感应电极阵列中心为原点)，感应电荷分布如图6所示。

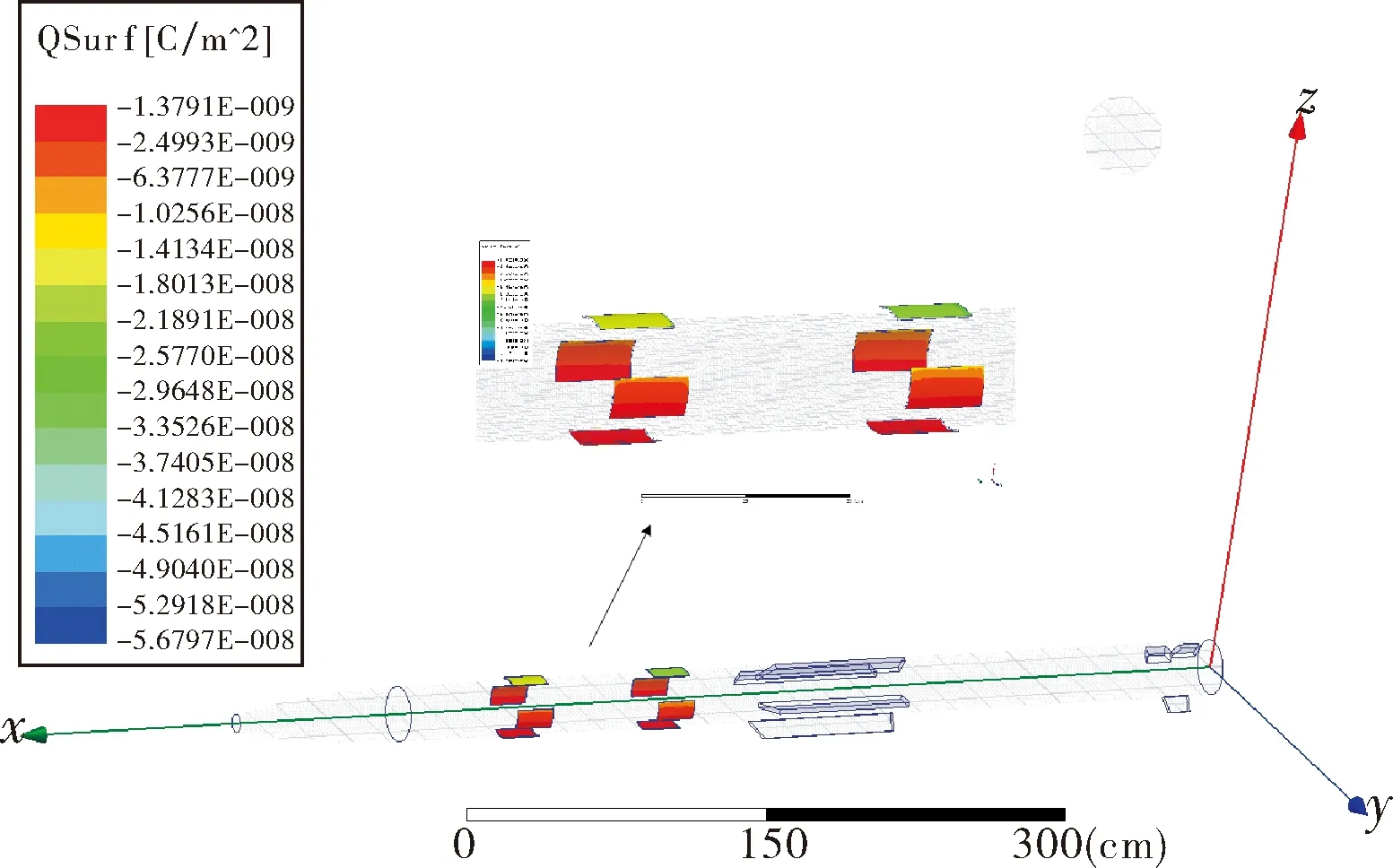
图6 感应电荷分布特性

从仿真结果可以看出，感应电极由于静电感应的作用获取与目标极性相反的电荷；感应电荷密度与弹目相对距离有关，随着距离的增大，感应电荷密度减小；同一感应电极平面上，感应电荷密度也不相等，距离目标(电荷源)较近的区域电荷密度较大；8个感应电极由于距离目标位置的不同，通过感应机理所获取的电荷密度不同。

3.5 交会特征信号分析

进行参数化建模计算，利用Maxwell场计算公式获取阵列感应电极的感应电荷总量，交会过程中感应电荷曲线如图7所示。

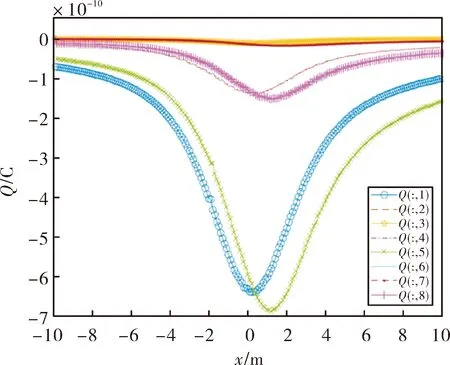
图7 感应电荷交会曲线

从计算结果可以看出，阵列分布的感应电极与目标在交会过程中，距离较近的感应电荷总量较大，在脱靶量点电荷量达到最大值；y轴方向的两对电极由于在交会过程中距离始终相等，计算获取的感应电荷量变化曲线趋于一致；由于导弹弹体(结构)的影响，目标空间静电场分布会发生改变，引起感应电极电荷总量存在差异。

4 结论

基于静电探测和静电场计算基本理论，建立弹目交会有限元数学模型，分析了目标静电场分布特性和感应电极表面电荷变化特征，指出目标静电场电荷分布与模型曲率相关，曲率越大电荷密度分布越高；感应电极获取电荷极性与目标极性相反，距离目标越近感应电荷密度越大。同时，采用参数化建模方法探讨了静电探测距离和感应电荷交会曲线，弹目距离为8.45 m时静电探测系统已具备探测目标的能力，交会过程中距离较近的感应电荷总量较大，在脱靶量点电荷量达到最大值。数值仿真计算能够验证和分析所建数学模型，同时为静电探测系统的优化设计提供理论支撑。在今后的工作中，需针对外界环境、交会轨迹以及介质材料等不同的条件，对静电探测系统开展深入的研究，为静电探测的工程化应用提供技术支持。