基于多假设解分离的CRAIM算法研究*

姚诗豪，李晓明，庞春雷

(空军工程大学信息与导航学院， 西安 710077)

0 引言

基于伪距的接收机自主完好性监测算法(RAIM)已经被广泛应用于各种场合，例如非精密进近[1]，然而由于定位精度的限制，基于伪距的定位和完好性监测无法满足III类精密进近和舰载机着舰等高精度定位的需求，此时必须采用基于载波相位的定位和完好性监测算法。

国内外很多学者对CRAIM算法进行了研究。文献[2]将扩展卡尔曼滤波推广到CRAIM算法中,可检测出超出完好性要求的故障，但无法进行故障识别。文献[3]认为载波相位测量误差并不符合高斯分布，提出了基于高斯和滤波器的CRAIM算法，降低了垂直保护水平，但是这种方法需要较大的计算量，只能应用于参考站、监控站或大型客机。文献[4-5]将历元间载波相位测量值差分构造检验统计量进行完好性监测，这种方法消除了整周模糊度，但是参考时刻的测量值需GNSS完好性通道信息进行修正，且协方差矩阵的分析比较复杂，保护水平的计算更加困难。文献[6]讨论了基于双频载波相位观测值的精密定位的完好性监测问题，并利用GLONASS 和GPS 双星座下的观测数据对算法进行了验证。文献[7]利用类似于最小二乘残差法的检验统计量对载波相位观测值中的故障进行了探测，但未考虑多故障的形式而且未给出用户保护水平的计算方法。

通过以上研究现状可知，CRAIM算法的发展处于起步阶段，对故障类型、完好性风险分配、用户保护水平计算等问题未进行深入研究。文中提出一种基于多假设解分离的多故障CRAIM算法，优化完好性风险分配和垂直保护门限，提高系统可用性。

1 多假设解分离方法

1.1 基本原理

MHSS算法是利用多元假设检验计算危险误导信息(HMI)概率的一种算法，H0表示无故障假设，Hi(i=0,1,…)表示存在故障模式i的假设[8]，若有n颗可见星，则共有N=2n种故障假设。PHi表示Hi发生的先验概率，设第j颗卫星发生故障的先验概率为Psat,j(j=1,2,…,n)，则Hi发生概率为[9]：

(1)

总的完好性风险可以表示为每种故障模式完好性风险的加权和，权重为故障发生的概率：

(2)

其中P(HMI|Hi)为故障模式i下的完好性风险，这样是为了计算定位误差保护限以使得真实位置落在误差保护限内的概率满足要求。

方法的基本思路是计算所有故障模式的定位解，对每一个解都可以计算出一个误差范围，这样最终能得到一个将所有误差范围包括在内的区间，使得真实位置位于区间外的概率小于PHMI[10]。

为满足完好性需求，对于每种故障模式，需要垂直定位误差满足：

(3)

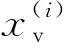
(4)

从实时VPL的定义可以看出，其值取决于实际的测量值。

一些情况下需要根据规定的连续性对无故障情况下的VPLRT进行预测，要求满足：

P(VPLRT>VPL)≤Pcont

(5)

根据VPLRT的定义可得：

(6)

连续性风险被分配到除H0假设外所有的故障假设中：

(7)

对每一种故障模式Mi满足：

(8)

VPL可定义为：

(9)

通过这样定义，同时满足了完好性和连续性，并且计算更为灵活，只要能计算每种故障的位置解和误差限就能导出VPL。

1.2 最优垂直保护级别计算

假设有n个观测量构成观测向量y，G为观测矩阵，观测量的标准差为σi，则有加权矩阵：

(10)

在实际计算过程中，可以由无故障的观测量实时计算每一个故障模式的定位解x(i)：

x(i)=Siy

(11)

Si=(GTEiCG)-1GTEiC

(12)

Ei为Hi故障假设中故障星对应的对角线元素置零的n×n阶单位矩阵。

观测值在垂直方向的方差和累积误差定义为[11]：

(13)

(14)

则Li可以定义为：

Li=KPHMI,i×σv,i+Bv,i

(15)

其中KPHMI,i由标准正态累积分布函数给出：

(16)

通过以上计算，满足了完好性风险要求。

为计算预测的VPL，需要计算Mi，定义：

(17)

(18)

(19)

那么，Mi表示为：

Mi=Kcont,i×σss,i+Bss,i

(20)

因此，垂直保护水平可以表示为：

(21)

根据式(9)可知，VPL为VPLi的最大值。

2 基于MHSS的 CRAIM算法

2.1 载波相位观测模型

短基线的用户接收机u和基准站接收机r同时跟踪卫星i，可构造单差载波相位观测方程为[12]:

φur=G·bur+e·fδtur-Nur+εur

(22)

解得单差整周模糊度后可得：

(23)

加权模型可以简写为：

Wy=WGx+Wε

(24)

权重矩阵为观测噪声均方差的倒数组成的对角阵。

2.2 改进最优VPL计算方法

将多假设解分离方法应用到加权单差载波相位观测模型。首先对VPL计算进行优化。从VPL的计算公式可以看出，可以对每种故障假设的完好性风险和连续性进行优化分配，使得VPL的值最小。用数学表达式描述为：

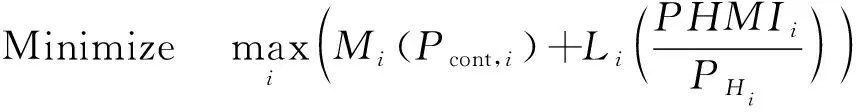
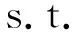
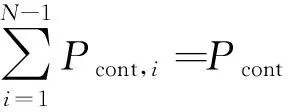
(25)

通过二维搜索和多次迭代运算进行求解，使完好性和连续性同时达到最优配置[13]。但是当故障模式较多时计算量较大，不利于用户接收机解算。考虑将式(25)转化为两个一维搜索，即对完好性风险和连续性风险分别优化分配，同时对其增加约束条件。优化完好性风险分配需满足的原则为：

(26)

将PHMI平均分配的实验结果显示，基本满足σv,i越大，Li越大的趋势，Li的最大值取决于σv,i最大的1～2种假设。由此可见，σv,i越大，KPHMI,i应越小，依据σv,i从大到小重新排序，σv,max对应的为KPHMI,min。所以可得：

2(1-Q(KPHMI,min))

(27)

可以解得：

(28)

由于

(29)

可得完好性风险的约束条件，即：

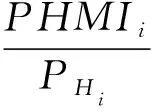
(30)

所以:

(31)

对于连续性风险，利用同样的方法求得极小极大的M值。就能得到要求的VPL值。

3 实验验证及性能分析

3.1 实验条件

为了验证单差载波相位模型下的MHSS算法的有效性，进行了GPS相对定位实验，基站和用户站均采用NovAtel板卡采集1 966个历元的载波相位数据，采样频率为1Hz。文中将分析算法计算VPL值的性能，实验过程中的各参数如表1所示：

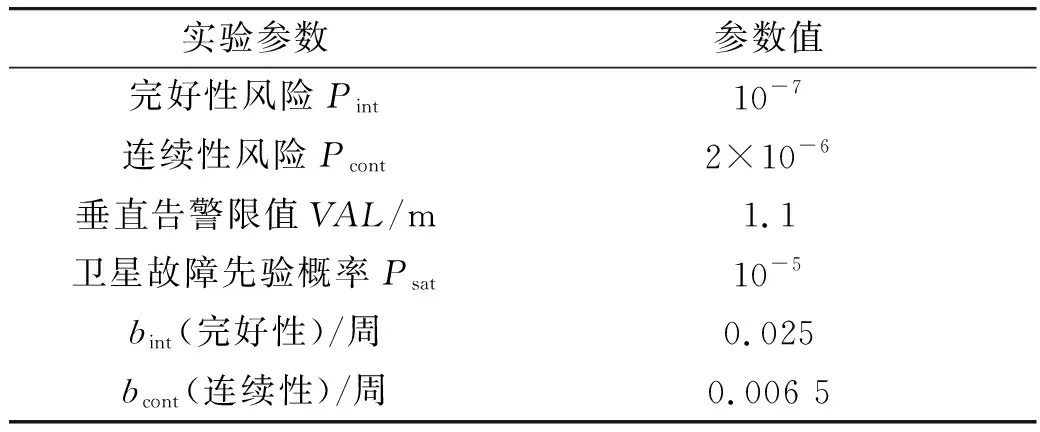
表1 实验参数设置

3.2 算法性能分析

利用设置的实验参数，计算垂直保护级别，得到图1所示VPL曲线图。

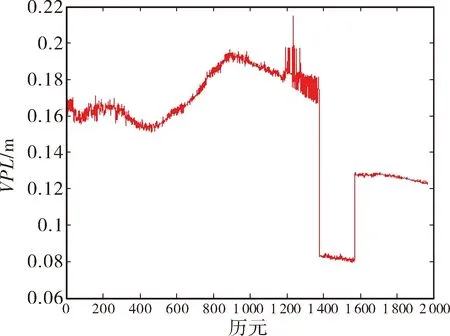
图1 VPL曲线图

由图1可以看出，VPL值小于VAL，算法满足可用性要求，卫星数目对VPL值有影响，可见星数增多，能使VPL值降低。

3.3 卫星故障先验概率对性能影响

实际过程中，卫星故障的先验概率发生变化，势必会对VPL的计算产生影响。为了评估不同卫星故障先验概率对算法的影响，文中对这一过程进行实验分析，取可见星为7颗情况下的1 375个历元的观测数据，卫星故障先验概率由10-7按等比数列的方式递增到10-3，共取5个概率值，观察对应的VPL变化情况，结果如图2所示。

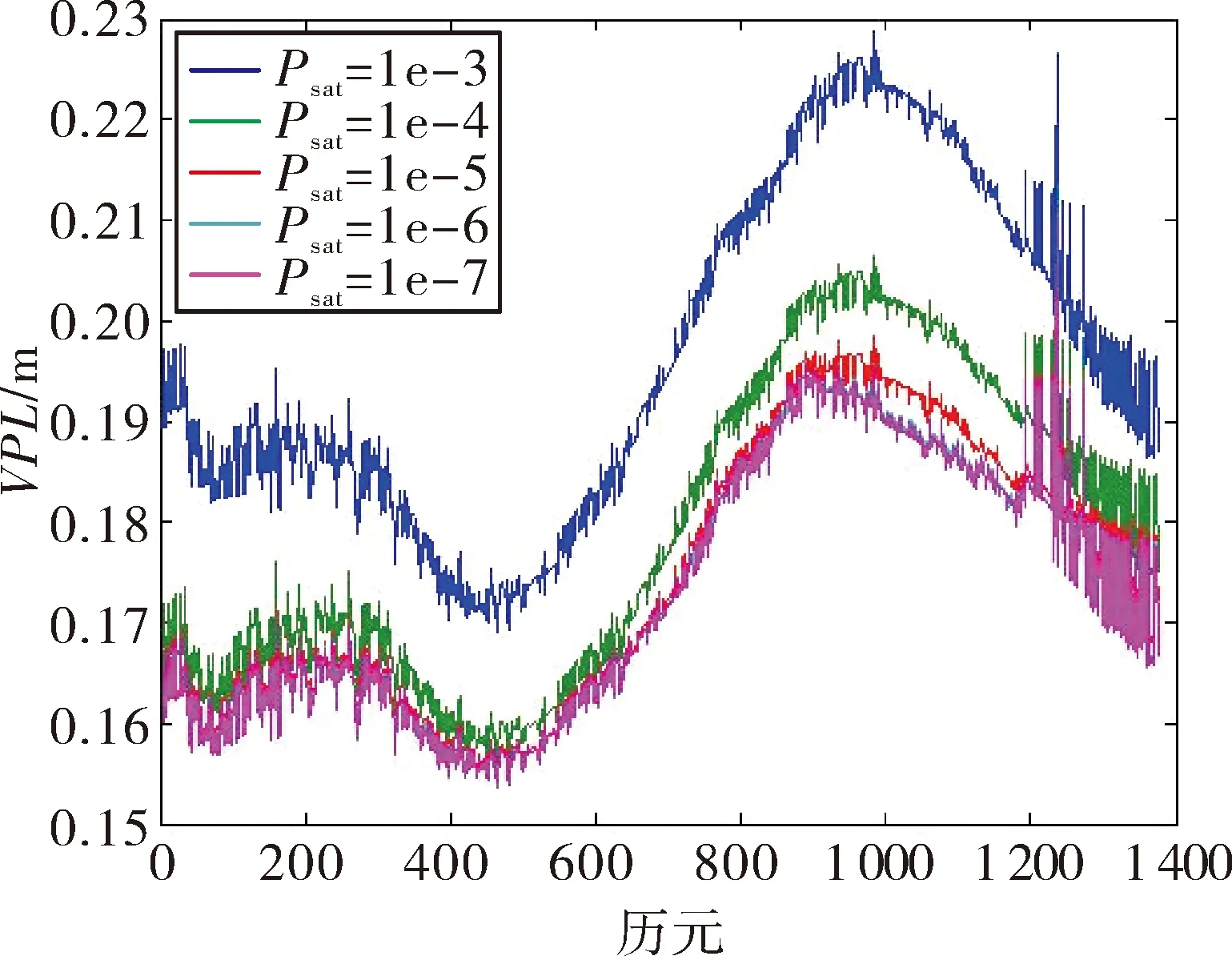
图2 卫星故障先验概率与VPL关系

由结果可以看出，卫星故障先验概率不同导致VPL值不同，卫星故障先验概率由10-7增加到10-4，相应的VPL值变化也随之增大，但是增长比较平稳，算法具有较好的稳定性。

3.4 测量偏差对性能影响

美国联邦航空管理局(FAA)定义了基于伪距的RAIM算法中距离测量偏差最大值bint和距离测量偏差标称值bcont，bint用来评估完好性，通常取值为0.75 m，bcont用来评估精度和连续性，通常取值0.1 m[14-15]。现在讨论CRAIM算法中相应参数，在单差模型中将bint定义为单差载波相位测量偏差最大值，bcont为标称值，均以周为单位。可见星为7颗，卫星故障先验概率为10-5，bcont设为0.006 5周，分别将bint设置为0.02周、0.025周、0.03周和0.035周，其结果如图3所示。接着对CRAIM算法中bcont的值对VPL的影响进行分析，可见星为7颗，卫星故障先验概率为10-5，bint设为0.025周，分别将bcont设置为0.004周、0.006 5周、0.008周和0.010周，其结果如图4所示。

图3 不同单差载波测量偏差最大值下VPL值

图4 不同单差载波测量偏差标称值下VPL值

从图3可以看出，VPL值随着bint的增大而增大，而且增长比较平稳。从图4可以看出，VPL值随着bcont的增大而增大，而且增长比较平稳，算法具有较好的稳定性。

4 结论

文中将多假设解分离算法应用于载波相位域，提出了约束条件下的改进算法，由此得到将完好性风险和连续性风险分别优化分配以计算最优VPL的CRAIM算法，实验结果表明，VPL值始终小于垂直告警限值，该方法能够满足Ⅲ类精密进近和舰载机着舰等高精度定位场合的可用性要求，并且可见星越多，可用性越高。同时，在不同卫星故障先验概率和测距偏差最大值下对算法性能进行实验分析，算法性能较为稳定。