改进ORB特征光流的飞行器室内导航方法*
2019-07-30郝志洋张虹波赵子君葛聪乐
郝志洋,张虹波,车 进,赵子君,葛聪乐
(1 宁夏大学物理与电子电气工程学院, 银川 750021;2 长春工业大学计算机科学与工程学院, 长春 130012)
0 引言
目前的飞行器应用主要集中在室外GPS环境下的定位与导航,在室内GPS缺失的环境下,飞行器的定位与导航正是近年来的研究热点。传统的视觉导航是飞行器采集图像,通过图传模块或者wifi等设备将采集的照片发送到地面终端,地面终端进行处理后再反馈给飞行器来完成导航。此类方法在无干扰或者干扰程度小的环境中使用,且反馈回的视频信息将压缩,缺失了实时性和鲁棒性。
针对于传统视觉导航方法的不足,文中提出一种基于改进ORB特征光流算法,对于传统光流算法不能获得完整光流信息和ORB算法自身缺失尺度不变性的缺点,将具有尺度不变性特点的SURF算法与ORB算法进行结合,并且通过PROSAC算法来剔除误匹配点,然后将所提取的高精度特征点的光流信息与惯导信息融合,来提高对飞行器速度的精确估计。
1 改进ORB光流的速度估计
1.1 ORB算法的特征点提取与描述
ORB是一种实时性较高的特征提取与描述算法,是将FAST特征点的检测方法与BRIEF特征描述子结合起来,并在其基础上做的改良。具体实现为:
1)建立图像高斯金字塔,对每一层图像提取FAST特征点。
2)为特征点增加方向因子。定义像素点到特征点的矩为:
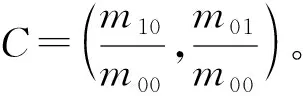
3)取一个S*S的像素块P,平滑处理后,利用二进制码串得到二值测试定义为:

式中I(p,x)是像素块P的中点x=(u,v)T的灰度值。生成的特征描述子即为n维二进制码串[3],如下:

用变换矩阵Rθ对S矩阵进行旋转,即可以得到新的描述矩阵SQ:
只要θ确定,结合S可以得到变换后的描述子:
gn(p,θ)=fn(p)|(xi,yi)∈Sθ
1.2 改进ORB算法
ORB算法是一种快速高效的特征点提取算法。当前较为成熟的关于特征点提取的算法主要有SIFT和SURF,了解到ORB算法提取特征点的速度是SIFT的两倍,SURF的一倍多[4]。而且,ORB算法本质上对于特征点提取采用的是FAST算法,而对于特征点的描述采用的是BRIEF算法,ORB算法是先将两者结合起来,然后在两者的基础上做了一些优化。
SURF算法是在SIFT算法的基础上提出的改进,提高了算法的执行效率,但其最大的优势是保持了SIFT算法的基于尺度空间的,对图像缩放、旋转、甚至仿射变换保持不变性的特点[5]。
SURF算法为了剔除重复特征点,构建了黑塞矩阵来生成兴趣点。设在尺度σ处,图像I(x,y)的Hessian矩阵定义为:
其中:Lxx(x,σ)是高斯函数二阶偏导数∂2g(σ)/∂x2与图像中的灰度值的二维卷积,Lxy(x,σ)、Lyy(x,σ)与Lnx(x,σ)的意义相似。
对上式的行列式进行近似化简可得:
Det=DxxDyy-0.9Dxy
其中Dxx、Dyy和Dxy分别是Lxx、Lyy和Lxy的近似值。由于SURF算法在极值点检测时采用了盒式滤波器来代替高斯滤波器,而盒式滤波器代替高斯二阶微分算子时,要加一定的权值,这里的0.9算是一个经验值,在实际使用中,用常量0.9表示其相对权重系数不会对结果产生较大的影响。
ORB算法虽然具备快速性的优点,但因为其本身使用FAST来检测特征点,在具备快速性特点的同时也损失了尺度不变性,为了弥补这个缺点,在后续算法步骤中,算法引入了特征方向来弥补缺点,但算法本身的特征描述子依旧不具备尺度不变性。考虑到飞行器在飞行过程中,自身传感器误差引起的抖动或者根据需求需要在飞行高度上调整,目标的大小就会发生变化,所以针对任务需要使得算法具备尺度不变性。为了解决这个问题,文中将SURF的尺度不变性特点和ORB算法快速性特点相结合,弥补了各自缺点。这样既保留了ORB算法描述子运算速度快的优点,又解决了ORB算法不具备尺度不变性的缺点[5]。将此改进的ORB算法定义为SURB算法。
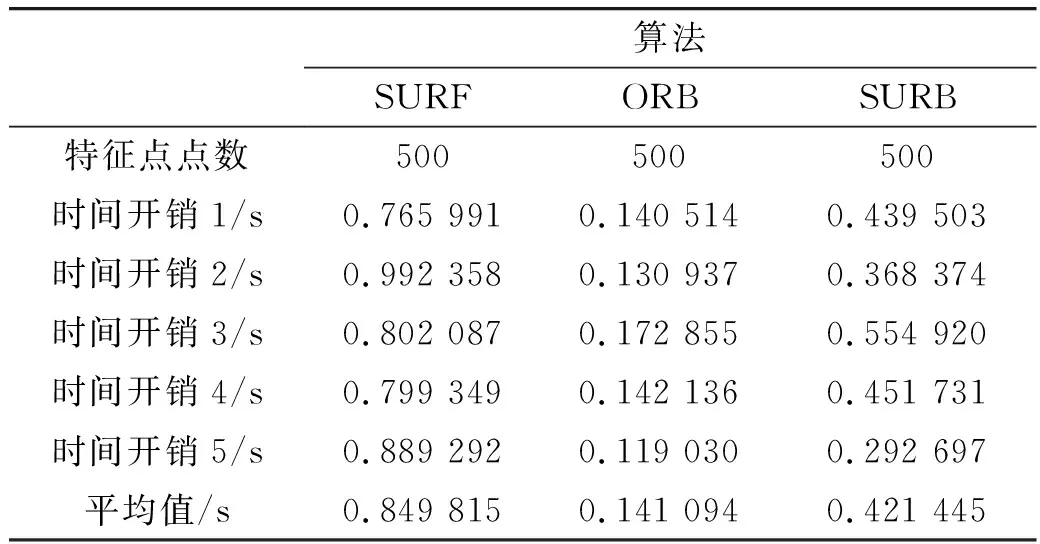
表1 各类算法时间开销
如表1所示,为了避免试验偶然性,采取多组试验验证当特征点数目为500时,ORB时间开销最短,SURB时间开销与ORB相差约280 ms,可近似视为相等,而SURF的时间与其余两种算法相差较大,有的甚至相差接近一个数量级。飞行器针对于飞行高度的变化,既要对尺度不变性有所要求,又对实时性要求较高,因此将改进的ORB算法用于稀疏光流法的特征提取上,可以减小时间开销,获得较高的实时性。
2 飞行器速度估计
2.1 通过SURB改进Lucas-Kanade光流提取
基于特征点的金字塔Lucas-Kanade算法(简称LK)是经典的光流提取算法,该算法需要基于亮度恒定,帧与帧之间运动范围小和空间一致性的假设[6]。I(u,v,t)表示t时刻像素点处图像的灰度值,基于上述假设可以得到像素点亮度的守恒方程:
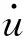
LK算法的3个假设在实际中很难满足,传统的解决方法有:1)保证足够大的图像帧速率。2)引入图像金字塔,通过不同尺度图像的光流提取来保证连续性。特征点匹配过程中,由于噪声等外界因素的影响,容易产生大量的误匹配点,经过汉明距离的匹配存在误匹配点产生匹配误差,影响匹配效果,PROSAC算法是通过多次迭代来达到去除误匹配点的目的。
PROSAC算法与RANSAC算法略有不同,PROSAC算法和RANSAC算法都是一个多次迭代来达到去除误匹配点目的的算法。但RANSAC是随机抽样的一个结果,也就是说RANSAC不能使最终的结果更准确,而PROSAC算法是先对所有匹配点的结果进行一个降序排序,不断选取最佳结果进行迭代,得到最优解,提高了精度。

图1 粗匹配

图2 PROSAC算法匹配
经过图1粗匹配和PROSAC算法(图2)双重特征点匹配后,得到的匹配点精确度有了明显提高,误匹配点也明显降低。
2.2 光流信息处理和惯导数据融合
摄像头在采集图像信息的过程中可能会受到干扰,进而产生视频不流畅或者图像出现条纹的状况,这将导致光流计算产生较大的误差[7]。应用卡尔曼滤波器,离散事件过程方程和测量方程表示如下:
Xk=AXk-1+ωk-1
Zk=HXk+ϑk
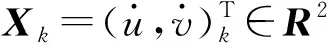
当相机没有水平移动而仅存在姿态变化时,依然会产生光流场,因此在实际由光流场解算速度时,考虑到姿态变化的影响。假设相机安装在飞机的正下方重心处,像平面与机体x-y平面平行。当机体发生如图3变化时,将惯性测量单元获得的姿态角数据与光流数据融合,可以消除光流旋转分量的影响,进一步提高对飞行器水平运动估计的精度[8]。

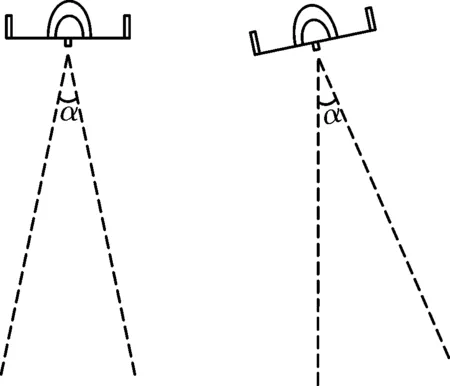
图3 飞行器姿态变化
根据针孔相机模型,知道摄像头的图像比例常数s、焦距f和飞行器的飞行高度h(这里近似飞行器的高度即为摄像头光心距离地面的高度),可以计算出飞行器实际水平位移:
式中:Δx和Δy分别是两帧图像之间x方向和y方向的飞机实际水平的位移增量;dxp,dyp是由上式计算出的光流水平分量。根据实际水平位移,矫正飞行器的姿态信息。
3 试验结果及分析
3.1 仿真试验平台搭建
四旋翼的结构简图如图4所示。飞行时,1号、3号旋翼始终和2号、4号旋翼旋转方向相反,旋转方向如图所示。4个旋翼由4个无刷电机控制,当4个电机的转速相同时,四旋翼将悬停或者做竖直方向的运动,减小一组中的一个同时增大另一组中的一个电机转速时,四旋翼将做俯仰或滚转运动。
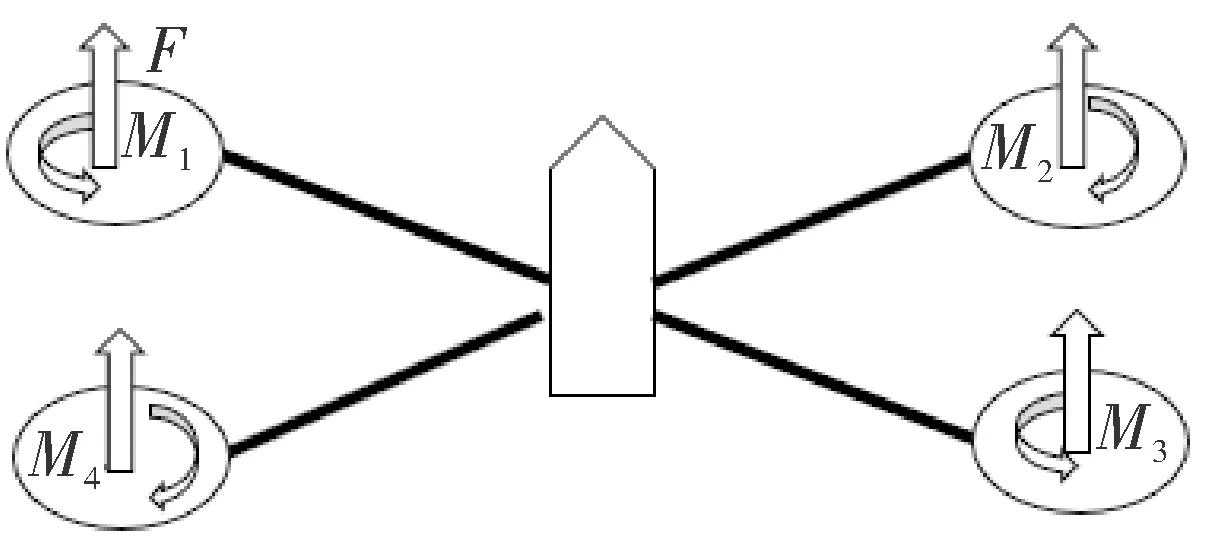
图4 四旋翼结构简图
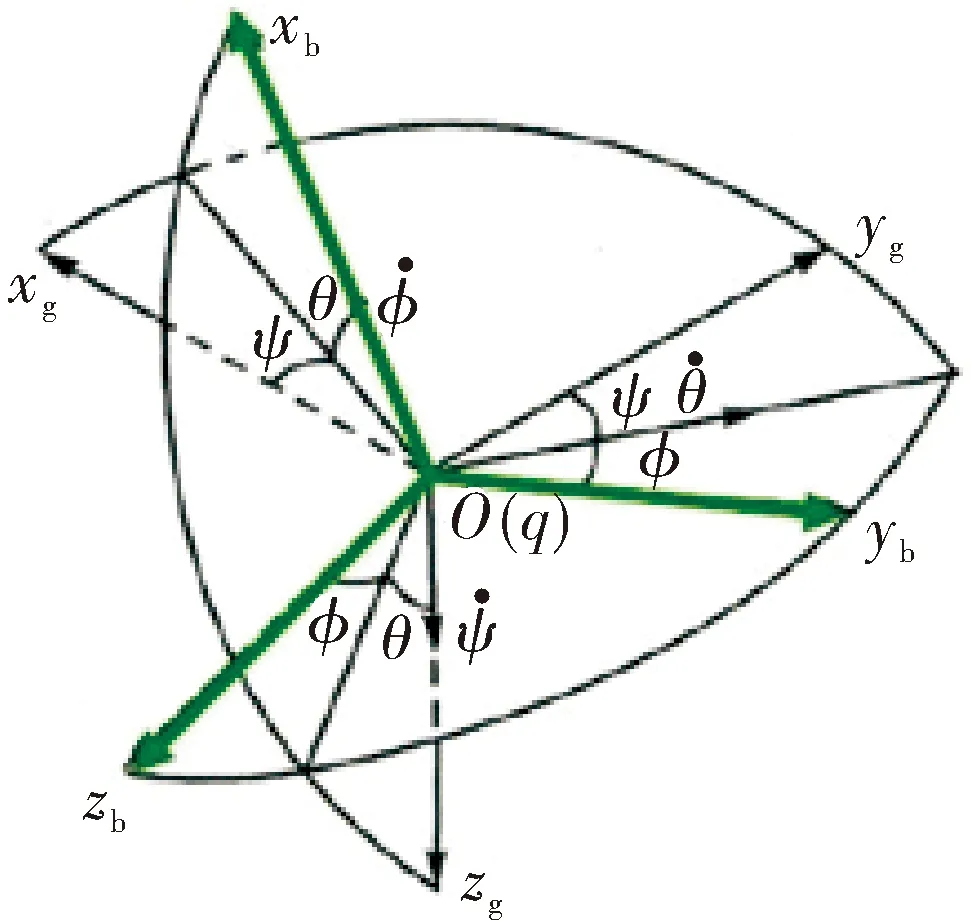
图5 坐标系
为了验证文中算法的合理性和优化算法性能,搭建了基于Matlab的仿真试验平台,利用Simulink建立模型。首先需要定义相关的坐标系(见图5)。O-xgygzg是地面惯性坐标系,即相对于地面固定的坐标系。o-xbybzb为机体坐标系,其原点o固定于机体重心,x、y轴固定于机身支架。其中θ是xb与平面O-xgyg的夹角,代表俯仰角度;ψ为机体坐标系xb轴在水平面上投影与地面坐标系xg轴(在水平面上,指向目标为正)之间的夹角,代表偏航角;φ为机体坐标系zb轴与通过机体xb轴的铅垂面间的夹角,代表滚转角。不考虑两个坐标系之间的线运动,即假设O与o相重合时,我们可以通过旋转使得两个坐标系相互重合。所以,可以获得两个坐标系的坐标转换矩阵:
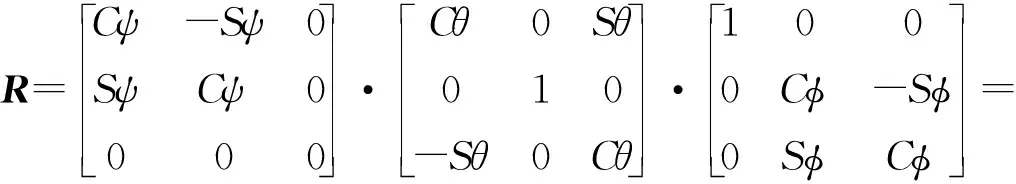
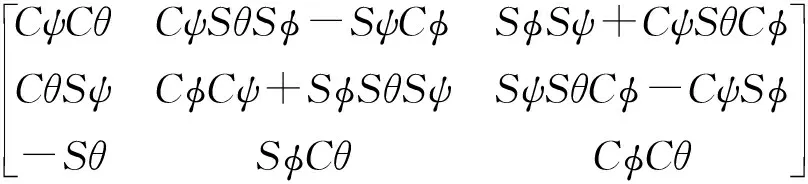
其中Sθ形式代表sinθ,其它的符号以此类推。ψ、θ、φ分别表示偏航、俯仰、滚转角度。在机体固连坐标系下,设4个旋翼的升力为Fi(i=1,2,3,4),则四旋翼受到的升力FB可表示为:
利用坐标转换矩阵R可得到地面惯性坐标系下的升力FE为:
FE=[FX,FY,FZ]T=U1[SφSψ+CψSθCφ,SψSθCφ-CψSφ,CφCθ]T
忽略四旋翼所受的空气阻力可得:
令IX、IY、IZ为四旋翼3个轴上的转动惯量,U2、U2、U4为四旋翼的滚转力矩、俯仰力矩和偏航力矩,假设四旋翼结构完全对称,忽略空气阻力和陀螺效应,四旋翼做小角度运动有:
最后得到四旋翼的简化数学模型为:
四旋翼的控制是通过调节4个旋翼的转速实现的。通过四旋翼的简化数学模型构造了两个控制器。一个是内环姿态回路控制器,用于控制四旋翼的姿态;一个是外环位置回路控制器,用于控制四旋翼的位置。得到如图6、图7、图8的仿真结果。
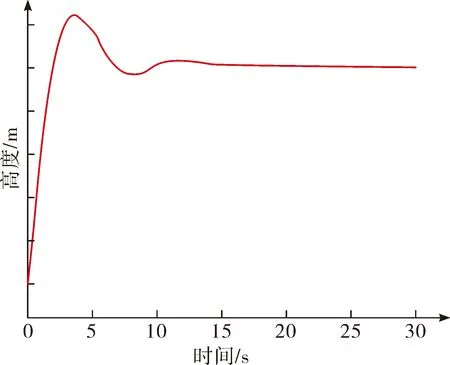
图6 Z位置曲线

图7 X变化范围曲线
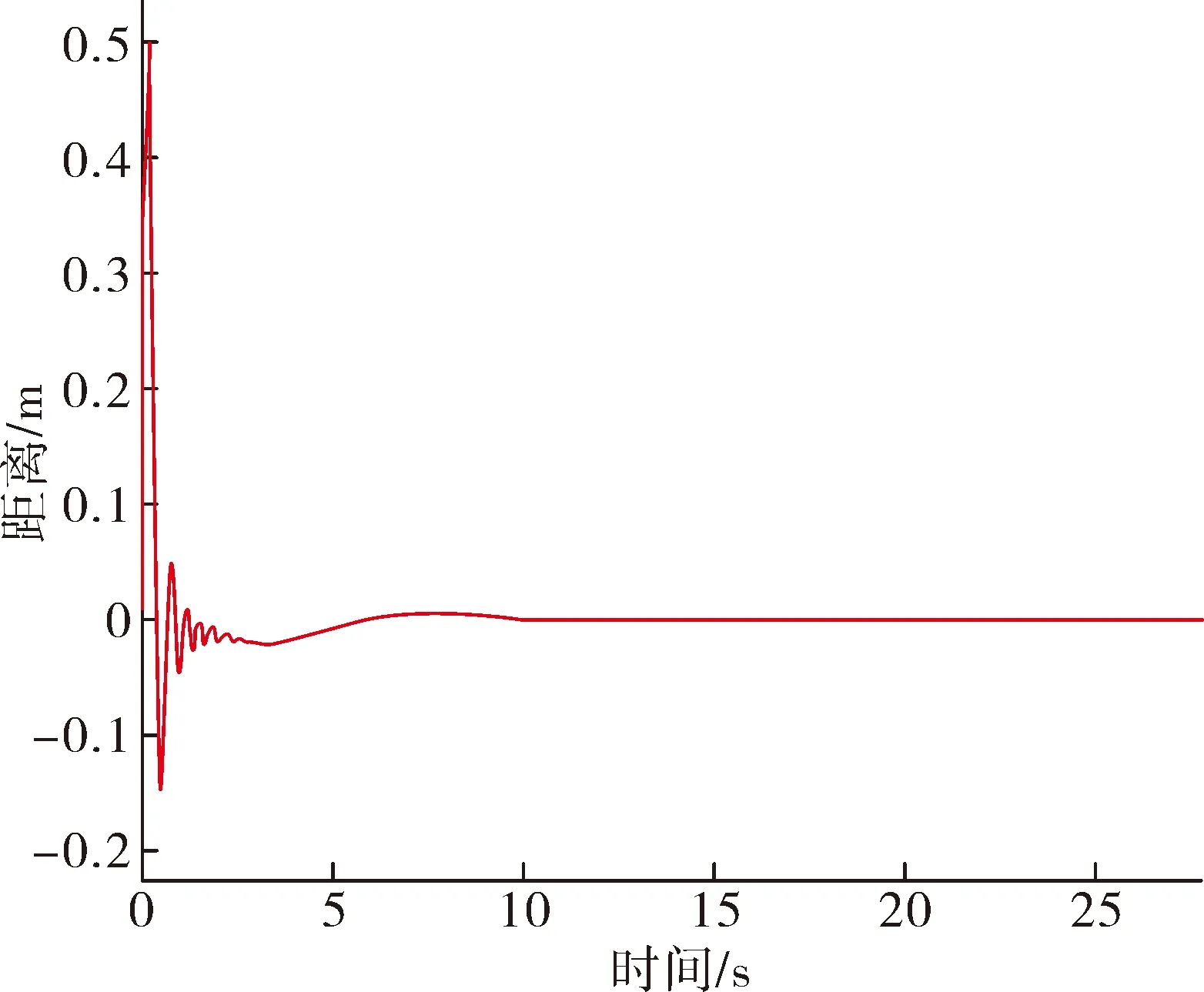
图8 Y变化范围曲线
通过观察仿真试验输出波形,Z位置的响应曲线以及X变化范围,Y变化范围曲线,可以看出本次模拟结果最终达到了稳定状态,且满足试验精度要求。
3.2 硬件试验平台
文中搭建了图9的四旋翼飞行器平台,以自动的方式操作飞行器起飞,实时记录数据,并将文中的算法用于飞行器控制中,验证飞行器的稳定性。
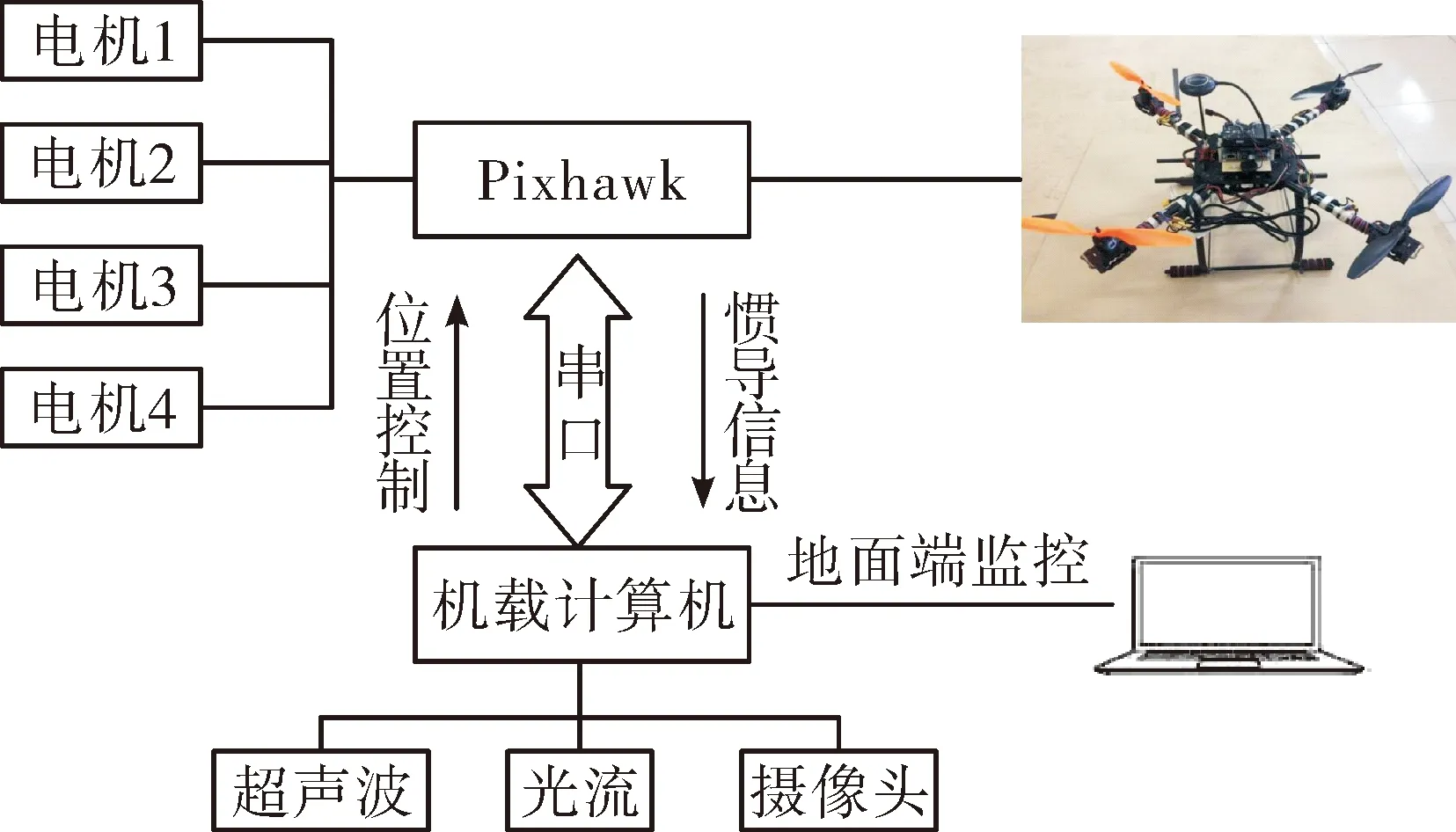
图9 试验平台框图
试验机载计算机订阅了local/position主题来获取飞行器当前的位置信息和状态信息,订阅了mavros的setpoint/local_position主题来发送目标位置,控制飞行器的起飞、悬停、降落[9]。期望高度为1 m,x、y的位置偏移量在0.3 m之内。从飞行控制板上读取的日志反映出本次试验的实际数据,飞行器高度、x方向偏移和y方向偏移的数据如图10~图12所示。
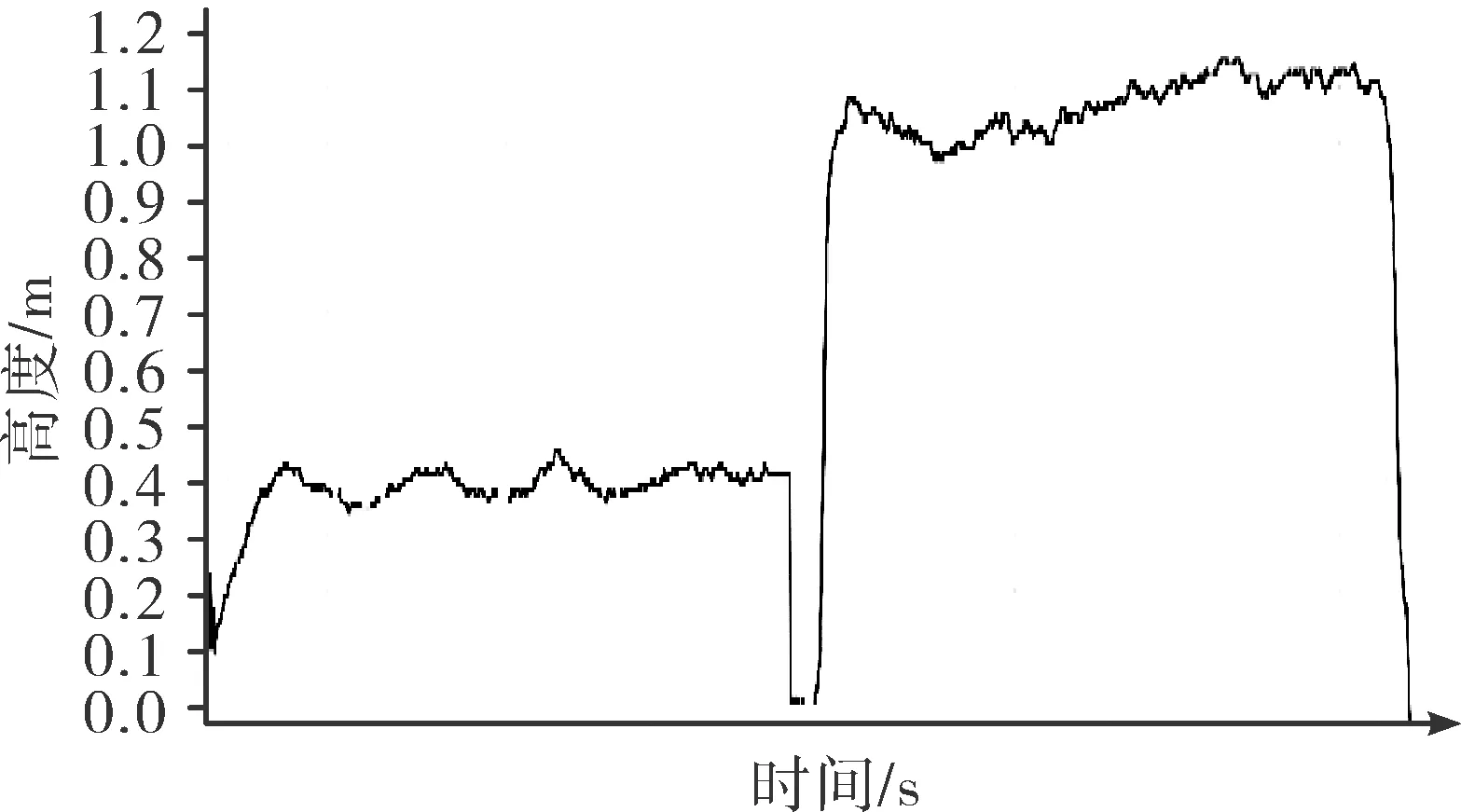
图10 飞行器高度
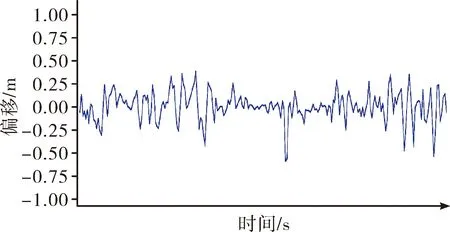
图11 飞行器x方向偏移
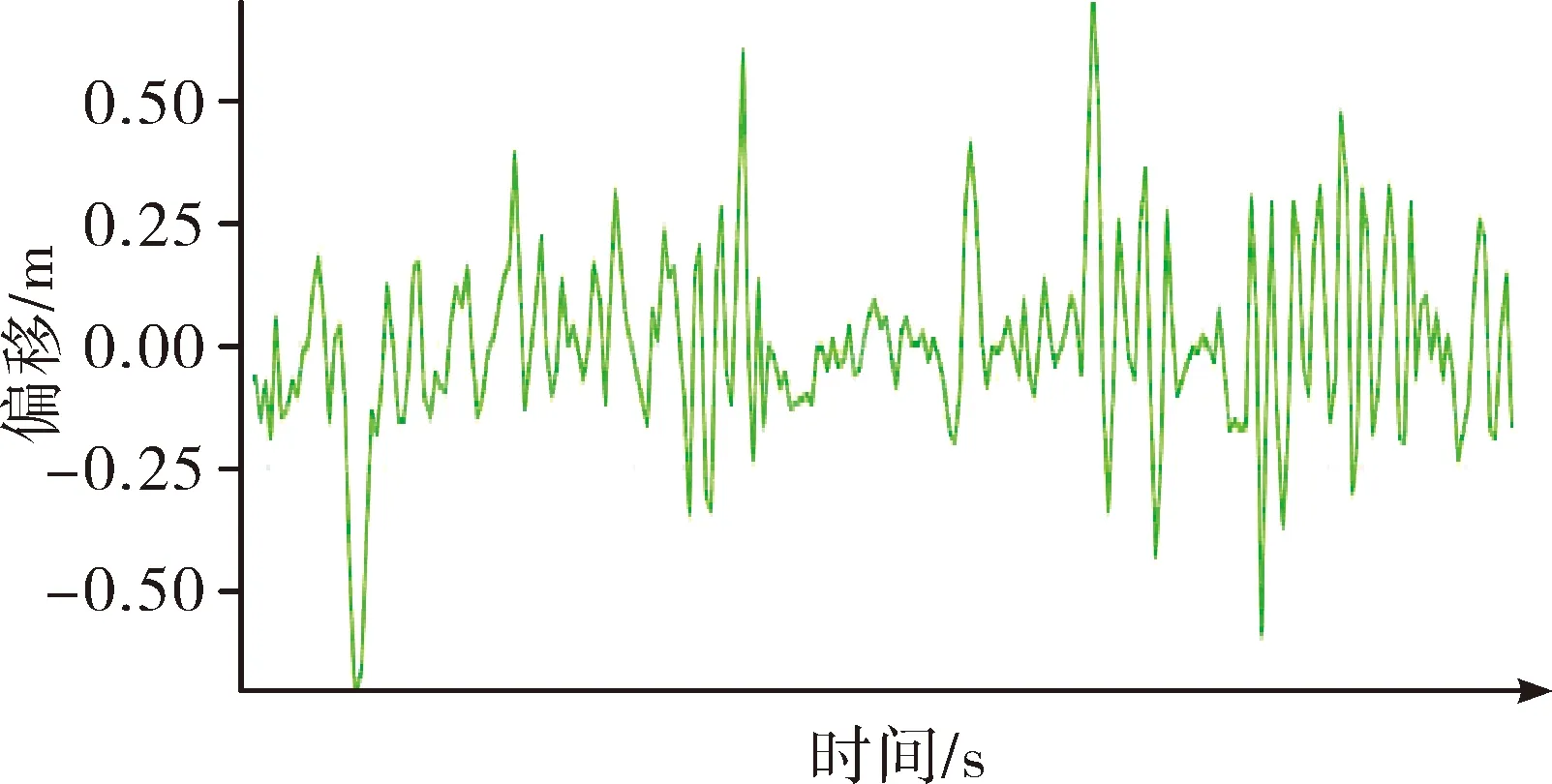
图12 飞行器y方向偏移
图11、图12分别是飞行器在x、y轴随着时间变化的曲线图,可以看出飞行器在悬停过程中,偏差范围基本满足在-0.25~0.25之间,悬停效果较好,系统姿态控制效果较为明显。且高度均保持在1 m左右,上下偏差范围0.1 m左右,满足本次试验的精度要求。从图中可以看出,系统高度控制良好,左右平移精度也基本稳定。
试验结果表明,四旋翼飞行器较为良好的实现了在室内通过机载计算机来达到起飞悬停、降落的目的,搭建的平台结构较为合理,控制算法也达到了预期要求。
4 结论
文中设计搭建了一套适用于在室内无GPS环境下的四旋翼飞行器自主起飞悬停的硬件平台,本次平台搭建采用了自行组装完成的机体,选取了odroid XU4作为上层的开发板,满足处理速度和精度的要求,并搭配了px4flow的智能光流传感器达到悬停平移校正的目的。试验结果表明:在光线良好且具有一定纹理的地面情况下,光流传感器可以计算出水平速度及位移量,并通过PID的反馈控制校正飞行器姿态,能够有效克服在室内无GPS环境下飞行器悬停飘移问题,基本满足试验的精度要求。
