岩石结构面抗剪强度MTS三轴试验方法研究

,张斌

(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059； 2.四川大学 水力学及 山区河流保护国家重点实验室，成都 610065； 3.中国华西工程设计建设有限公司，成都 610031)

1 研究背景

不规则、无充填岩石节理是岩体中一种常见的不连续面,通常多采用直剪法对不规则、无充填岩石节理进行剪切试验[1]。直剪法试验是通过每个试样的定值法向应力获得对应的剪应力，对多个试件分别进行试验，然后绘制正应力和剪应力关系曲线，最终获得抗剪强度指标。

由于实际工作中要获得同一岩石节理的多个试件十分困难，且也难以保证各试件节理面的粗糙度、起伏等特征相同，直剪法试验时也常对同一岩石节理试件进行多级试验[2-3]，即单试件直剪试验。然而，单试件直剪试验只有在低正应力条件下所获得的峰值剪切强度才比较可靠[4-6]。尽管同一试件重复进行直剪会使得余下的试验结果落在峰值强度和残余强度之间，然而受试验方法和设备的限制，目前单试件直剪试验法仍被广泛采用[7-8]。

本文尝试在电液伺服岩石试验系统(MTS)上对含不规则、无充填结构面的岩石试样进行三轴试验。与常规岩石三轴试验一样，保持试件在围压不变下逐渐增加轴向压力直至最大轴向压力，则此加载过程中作用在节理面的正应力和剪应力均在增加。而利用伺服系统控制围压和轴向加载速率，对同一试件可连续获得不同围压下的最大轴向压力。然后根据弹性力学理论可求得同一试件不同围压下结构面的正应力和剪应力，对试验结果按线性Mohr-Coulomb准则拟合即可获得内摩擦角和内聚力，最后通过比较，对试验结果进行了验证。

2 试验仪器和方法

试验仪器采用MTS815型电液伺服岩石试验系统。试验设备主要由试验主机、液压源系统和数字控制系统3部分组成。岩石节理试件三轴试验采用常规三轴试验法，即在围压不变(σ2=σ3)下逐渐进行轴向加载，直至本级围压下的最大轴压σ1。利用伺服控制系统可对同一试件连续施加多级围压，从而获得不同围压下的最大轴压。轴向加载时应变速率为0.01 mm/s。所采用的试样岩性为二长岩，天然岩石结构面已完全分离、起伏粗糙、无充填、无胶结。

试验具体过程及注意事项如下：

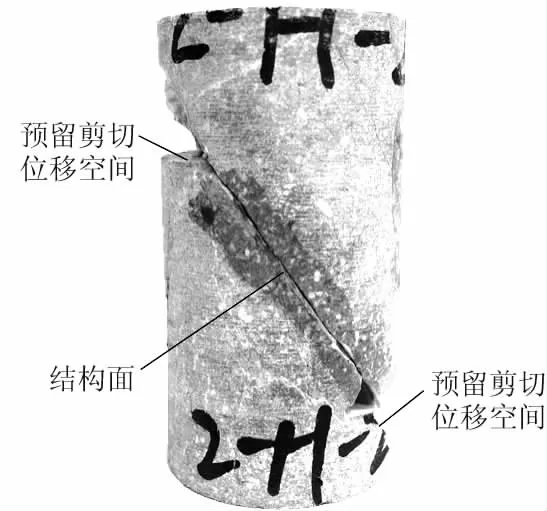
图1 典型岩石结构面试样制备Fig.1 Test specimen contai-ning typical structural plane

(1)含岩石节理的试件高度为直径的2倍。节理面上、下两端位置用金刚石锯切割预留10～20 mm的最大滑移空间，以保证在不同围压下轴向加载过程中节理面上、下块体能自由滑动(图1)。试验中以结构面上、下块体滑动位移达到预留的10～20 mm为试验终止条件。

(2)三轴试验中试件的围压是通过增加压力室内的油压来实现的。如果含岩石节理的试件直接置于液压油中，液压油将进入不连续面而无法对试件施加围压。为防止液压油进入不连续面，在试件外套上防油密封材料(图2)。试件密封过程尽可能地让节理面上、下块体完全接触。

图2 密封材料以防止液压油进入试样内部Fig.2 Wrapping to prevent hydraulic oil into rockjoint fissure

在获得围压对应的最大轴压后，根据弹性力学理论，可按式(1)—式(2)计算节理面的正应力和剪应力。

(1)

(2)

式中：σnj为节理面的正应力；τj为节理面的剪应力；σ1为轴压，即最大主应力；σ3为围压，即最小主应力，σ2=σ3；βj为节理面的倾角，即最大主应力作用面与节理面的夹角。

3 试验结果讨论与分析

3.1 试验结果

本次试验现场在钻孔岩芯中选取了13个岩石结构面试件，根据上述提出的三轴试验方法进行试验，获得的不同围压对应的最大轴向压力结果见表1，限于篇幅，仅列出部分予以展示。按式(1)和式(2)计算获得的正应力和剪应力，根据各试件的正应力和剪应力关系获得的节理面摩擦角φj和黏聚力cj也列于表1。

表1 岩石节理三轴试验成果Table 1 Triaxial test results of rock joint specimens

需要说明的是，尽管天然状态下结构面已完全分开，但因裂隙壁粗糙，剪切过程中会出现咬合摩擦，因此内聚力较小。同时，由于部分结构面壁凹凸不平(图3)，最后几级围压较大的情况下，凹凸不平的部位嵌合更为紧密，导致接近正应力增幅的条件下剪应力增加的幅度很大，最终的结果是利用Mohr-Coulomb准则拟合的曲线截距为负值，即内聚力为负值。出现这一现象的试样较少。

图3 试验后节理面的剪切压碎特征Fig.3 Fresh irregular shear parts on rock joint plane

3.2 试验结果验证

绘制所有试件的正应力和剪应力关系，见图4。图4中的(σnj,τj)散点关系表明，随着正应力的增加,剪应力也相应增加，且正应力和剪应力关系具明显的非线性特征。

图4 岩石节理正应力和剪应力关系及不同型式拟合曲线Fig.4 Fitting curves of the σnj-τj space

为了合理评估岩石结构面的正应力和剪应力关系，利用MatLab软件的曲线拟合工具分别进行Mohr-Coulomb准则线性拟合、幂函数拟合和Barton公式非线性拟合，拟合公式分别见式(3)— 式(5)。

τj=σnjtanφj+cj；

(3)

(4)

(5)

式中：a和b为幂函数拟合参数；φb为节理面的基本摩擦角(°)；JRC为节理面的粗糙系数；JCS为节理面壁的抗压强度。

幂函数拟合时先对正应力和剪应力取自然对数，则式(4)变为式(6)的线性表达形式。

lnτj=blnσnj+lna。

(6)

式(3)和式(6)可直接用最小二乘法求得未知系数。 式(5)可利用General Equation模块通过迭代求得未知系数。 General Equation模块中用户可输入任意形式的公式， 迭代求解Barton公式基本参数时， 先对各基本参数设置一个起始迭代值， 并给定各基本参数的可能上限和下限。 各基本参数起始迭代值及可能的上限和下限需满足Barton公式的物理意义。 拟合获得的各关系曲线绘制于图4中。

根据图4中不同类型拟合曲线的形态和分布特征可知：

(1)以本文方法获得的试验数据拟合的幂函数关系曲线与被工程和科研人员广泛认可及利用的Barton公式拟合的曲线几乎重合，这就能够说明岩石结构面三轴试验所获得的数据、数据序列的分布位置以及点群分布规律等都吻合国际上通用的Barton公式，表明所提出的试验方法是可行、可靠的。

(2)3种拟合关系的结果表明，用线性Mohr-Coulomb准则拟合明显比幂函数拟合和Barton公式拟合效果要差，尤其是在低正应力条件下，采用线性Mohr-Coulomb准则拟合将高估岩石结构面的剪切强度，所以本文所提出的方法不仅更加便捷，获得的计算式在体现岩石结构面真实的抗剪强度特性方面也更为精确，且总体反映了岩石节理剪切强度的非线性特征。

(3)在较高正应力下，线性Mohr-Coulomb准则、幂函数和非线性Barton公式对应的剪切强度均偏高。以Barton公式拟合的结果为例来分析。Barton公式中涉及到结构面粗糙程度参数JCS，JCS通过经验公式估算获得[9]。分别将试验获得的σnj和τj除以JCS，并绘制σnj/JCS和τj/JCS关系于图5中。根据图5中点分布与曲线形态可见，当0.01<σnj/JCS<0.3时Barton公式估计的岩石结构面剪切强度是比较可靠的，而当σnj/JCS>0.3时Barton公式估计的岩石节理剪切强度将偏高。

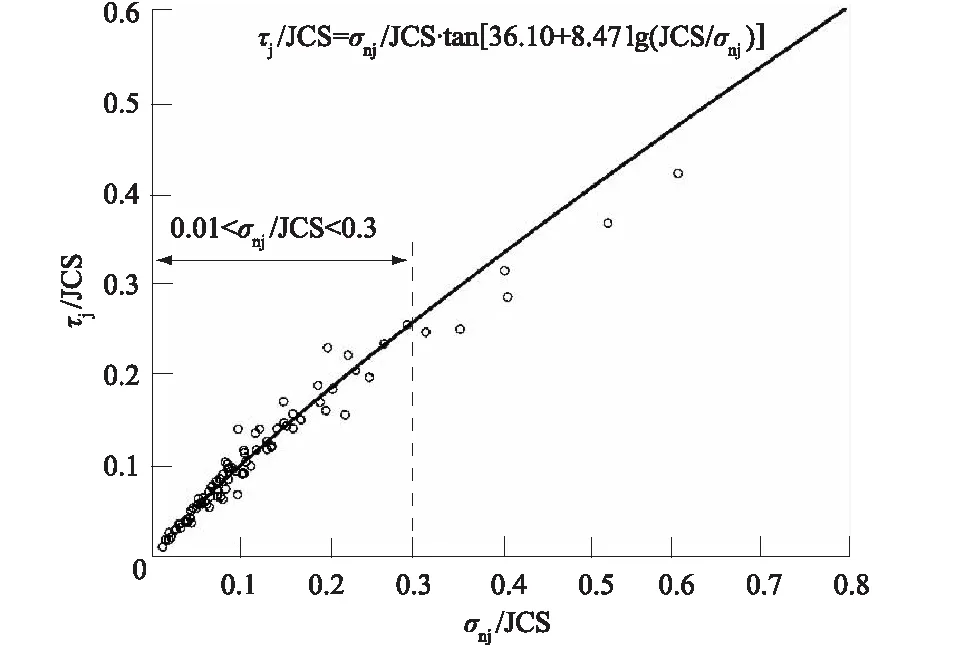
图5 岩石节理剪切强度试验及取值方法的可靠范围Fig.5 Reliable range of rock joint shear strengthobtained by test method

出现这一问题主要是由于同一试件重复进行剪切时，较高正应力下获得的剪切强度落在峰值强度和残余强度之间。尽管本文介绍的岩石节理三轴试验是在连续施加多级围压下进行的，但是在前面几级围压下节理面上、下滑动过程必然会使节理壁局部凸起部位剪切破碎，从而使得后面几级围压下对应的剪切强度偏低，这也是本文所提出方法的局限，也是目前被广泛应用的单点法以及著名的Barton公式等试验或取值方法均未能克服的问题。

4 结 论

(1)本文提出了岩石结构面MTS三轴试验方法，即通过伺服设备控制施加围压，可以获得不同围压下的正应力和剪应力，最后通过Mohr-Coulomb准则线性拟合、幂函数拟合和Barton公式非线性拟合获得节理的强度参数。

(2)试验方法原理可行，克服了多个试件直剪试验中取样困难、各试件结构面性状难以统一、试验结果离散性大等缺点，并且相对于单试件直剪试验也有了较大发展，试验方法更为简单、快速，也可获得更为丰富的试验数据。

(3) 在试验结果上，幂函数拟合和Barton公式拟合能够反映岩石节理剪切强度的非线性特征，优于Mohr-Coulomb准则拟合；当0.01<σnj/JCS <0.3时，幂函数拟合和Barton公式拟合岩石结构面剪切强度比较可靠，而当σnj/JCS>0.3时获得的剪切强度偏高。