泵站流道导流隔水墙对结构内力分布的影响分析

邱 辉， 侯继平

（中国电建集团华东勘测设计研究院有限公司，浙江 杭州 310014）

1 工程概况

大治河排涝泵站工程位于杭州市萧山区大治河和钱塘江交汇口处，泵站设计排涝流量100.0 m3/s，采用5台立式轴流泵[1]。主泵房顺水流向长35.00 m，分为2台泵一跨和3台泵一跨，共2个结构段。每台泵设独立流道，每孔净宽7.50 m，中墩厚1.80 m，左侧边墩厚1.50 m（靠水闸），右侧边墩厚2.00 m。进水流道底板顶面高程-3.10 m，底板厚1.50 m；进水流道顶板底高程-0.40 ～ 0.30 m，厚度1.42 ～ 1.79 m。工程平面布置见图1。

图 1 工程平面布置图

为改善进水流道内水流的流态和进水流道顶板与底板的受力状态，在进水流道内增设导流隔水墙。本文以3台泵一跨的结构段为例，采用ANSYS平面有限元方法分析导流隔水墙在不同厚度d的情况下，进水流道底板、顶部、闸墩和导流隔水墙受力情况的变化规律，从而结合水流要求最终确定合适的导流隔水墙尺寸。

2 计算假定和荷载

2.1 计算假定和荷载

根据泵站设计规范:进水流道由导流隔水墙分成双孔矩形断面时，可按对称框架结构进行计算[2]。本工程闸墩、底板和顶板厚度较大，在计算中考虑其厚度的影响，即考虑剪切变形及节点刚性的影响。选取距上游7.00 m的横断面为研究对象，荷载有自重、外水压力、内水压力、土压力、设备重、扬压力和桩基反力。土压力按静止土压力进行计算，取静止土压力系数K0= 0.4；桩基反力根据整体稳定计算结果和桩基计算结果，按承台扩散为均布荷载进行计算；渗透压力按阻力系数法进行计算。计算中遵循以下假定:①选取单宽平面框架计算，考虑相邻框架之间的不平衡剪力[3]；②按倒置框架结构计算流道内力[4]。

2.2 计算断面的选择

从控制结构尺寸和配筋角度考虑，选取检修门槽后、技术供水泵房的A - A剖面为计算截面。泵站流道纵剖面见图2，进水流道横剖面见图3。

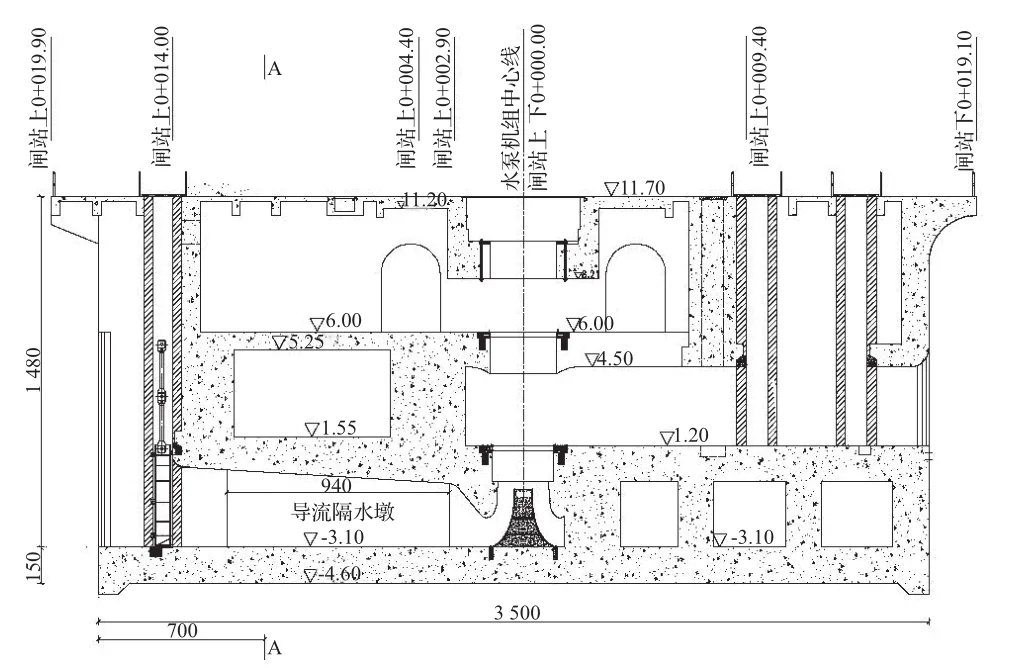
图 2 泵站流道纵剖面图

图 3 泵站进水流道横剖面图

2.3 计算工况的选择

为充分分析进水流道的内力情况，选择以下5种工况进行分析:

（1）正常运行工程（3台泵同时运行）:内河为常运行水位4.20 m，外江为最高运行水位7.90 m；

（2）完建工况:内河和外江均为无水；

（3）检修工况（3台泵同时检修）:内河为常水位4.20 m，外江为平均潮位3.80 m；

（4）检修工况（旁边2台泵同时检修）:内河为常水位4.20 m，外江为平均潮位3.80 m；

（5）最大扬程排涝工况（3台泵同时运行）:内河为最低运行水位2.50 m，外江为100 a一遇高潮位8.70 m。

3 计算模型

ANSYS分析软件已广泛应用于土木工程、水利工程等领域。本文将流道顶板、底板和墩墙按BEAM4模拟，刚性节点处弹性模量为C35混凝土弹性模量的5倍，取单宽框架结构进行分析。模型对BEAM4单元采用lesize = 0.3均匀划分，共划分单元数472个，节点数937个。模型顶部2个节点A、B采用铰支约束。有限元模型见图4。

图 4 有限元模型图

4 计算结果分析

以完建工程为例，有无导流隔水墙流道弯矩分布见图5 ～ 6。

图 5 无导流隔水墙弯矩分布图 单位:kN · m

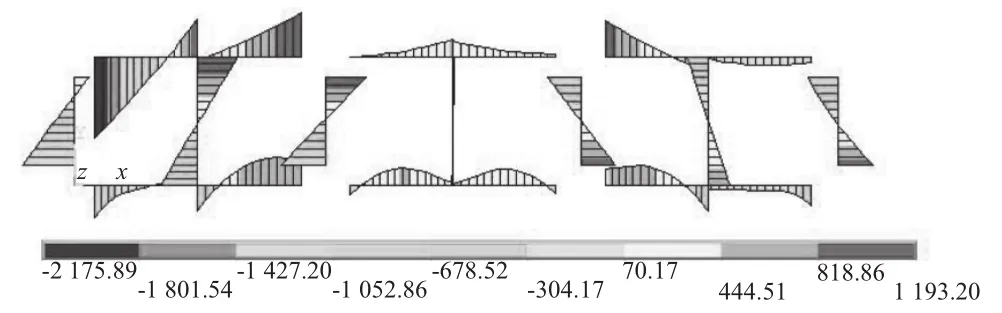
图 6 有导流隔水墙弯矩分布图 单位:kN · m

4.1 对顶板、底板和闸墩的影响

由图5、图6弯矩图形状和数值结果可知:

（1）导流隔水墙的设置改变了框架的受力特点，无导流隔水墙框架底板最大正弯矩发生在约跨中位置，设置导流隔水墙后，最大正弯矩向新框架跨中移动；

（2）未设置导流隔水墙时，底板最大负弯矩和最大正弯矩均发生在最大扬程排涝工况（3台泵同时运行），分别为-1 996.91，1 393.98 kN · m；设置导流隔水墙后，底板最大负弯矩和最大正弯矩均发生在最大扬程排涝工况（3台泵同时运行），底板最大负弯矩和最大正弯矩减小30.00% ～ 40.00%、顶板最大正弯矩减小25.00%，随着导流隔水墙厚度增加，弯矩继续减小，但底板最大负弯矩和最大正弯矩减小幅度7.30% ～ 2.46%、顶板最大正弯矩减小幅度7.00% ～ 2.00%，在导流隔水墙厚度为0.60 m以上时，各弯矩值减小幅度均在3.00%以内；

（3）未设置导流隔水墙时，顶板最大负弯矩发生在最大扬程排涝工况（3台泵同时运行），为-2 572.72 kN · m，顶板最大负弯矩在设置导流隔水墙后减小，在导流隔水墙厚度0.60 m时，顶板最大负弯矩为-2 175.89 kN · m，减小约15.00%；在导流隔水墙厚度0.80 m时，顶板最大负弯矩为-2 052.17 kN · m，减小约20.00%；随着导流隔水墙厚度增加，弯矩值减小幅度均在3.00%以内，增幅不明显；

（4）设置导流隔水墙后，闸墩最大负弯矩弯矩减小23.00% ～ 29.00%，随着导流隔水墙厚度增加，弯矩继续减小幅度不大，均在1.50%以内。

流道底板最大负弯矩结果见图7，最大正弯矩结果见图8；流道顶板最大负弯矩结果见图9，最大正弯矩结果见图10；闸墩最大弯矩结果见图11。

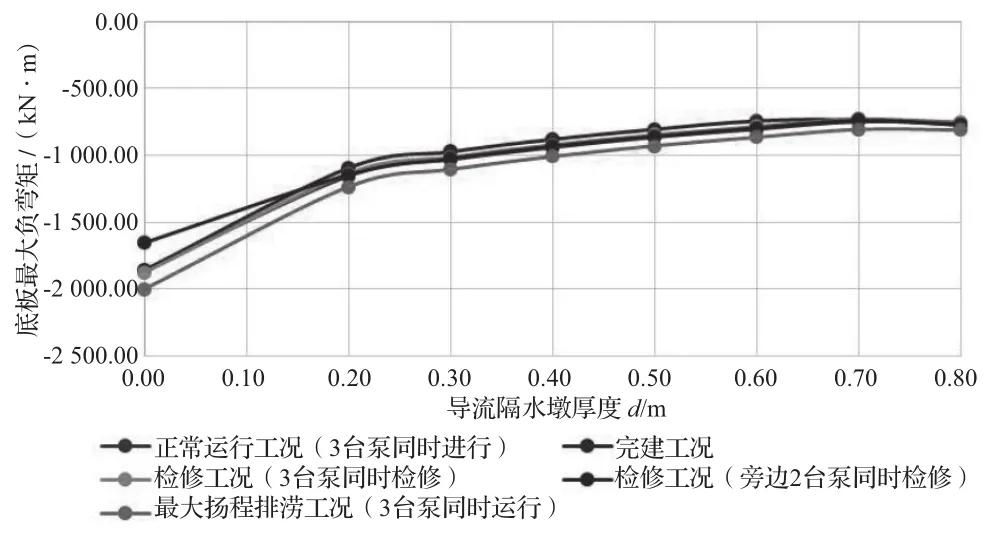
图 7 流道底板最大负弯矩结果图

图 8 流道底板最大正弯矩结果图

图 9 流道顶板最大负弯矩结果图

图 10 流道顶板最大正弯矩结果图

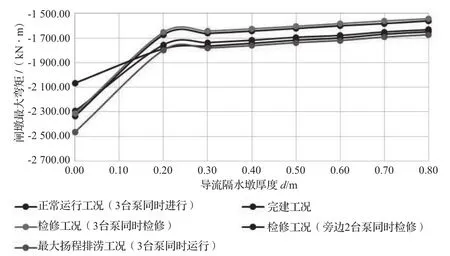
图 11 闸墩最大弯矩结果图

4.2 对导流隔水墩自身的影响

导流隔水墙自身弯矩随厚度增加而增加，依次增长幅度为33.00% ～ 5.00%。导流隔水墙最大弯矩结果见图12。

图 12 导流隔水墙最大弯矩结果图

4.3 导流隔水墙厚度的选定

根据各工况分析计算结果:在导流隔水墙厚度在0.60 m以上时，对底板、顶板弯矩减小有限，影响值趋于不明显。此时，导流隔水墙自身弯矩最大值1 093.43 kN · m，相应轴力为882.695 kN，按偏心受压构件进行配筋。

5 结 语

当流道跨度较大，为改善进水流道内水流的流态设置导流隔水墙后，减小弯矩计算跨度，流道顶板和底板的弯矩影响明显，但在导流隔水墩厚度在0.60 m以上时，弯矩影响较小；闸墩弯矩变化对导流隔水墙厚度不敏感，主要是受外荷载影响；导流隔水墙自身弯矩随厚度直线性增加，由于其为压弯构件，弯矩和轴力的增加对自身结构稳定不利。选择导流隔水墙厚度，在满足进水流道流态良好的前提下，应首先考虑满足导流隔水墙自身结构稳定要求，可选择底板和顶板弯矩随厚度增加而减小不明显的值作为最终导流隔水墙的厚度。