基于EMD算法的建筑墙体夏季室外计算逐时综合温度谐波研究

王翠红，王晓璐，鞠全勇，吴敏，周洪，杨建林

(1.金陵科技学院 机电工程学院，江苏 南京 211169；

2.南京航空航天大学 航空宇航学院，江苏 南京 211106)

0 引言

在暖通空调工程中，建筑墙体室外计算逐时综合温度是一个重要的基础参数。无论是计算建筑内部空调负荷，还是用数值方法计算墙体内部传热过程，均需要该参数作为热流场的边界条件。

虽然目前在暖通空调规范中，已经给出夏季空调标准设计日的室外计算逐时综合温度计算公式，但只是设计日一天的标准温度[1]。而我国地形条件复杂，不同地区温度差异较大，同一地区规范中的理论值与该地区建筑墙体实测温度也有一定差异[2]。为适应建筑节能墙体以及各种工业设备和管道的夏季传热负荷计算的实际需要，急需以夏季实测数据为基础，使用信号分析技术对夏季室外计算逐时综合温度谐波实时特性进行基础研究。

在建筑节能领域，由于墙体温度与热流的信号受天气及外界气象环境因素影响较大，本质上属于周期性变化、非平稳非线性信号，其中也包括大量随机变化的波动信号。传统傅里叶温度和热流谐波分析中无法揭示信号中各时段中出现的频率、波动的幅度随着时间变化情况，已经不能适应夏季墙体温度和热流谐波分析的要求，成为建筑节能研究数字化、智能化的一个短板。

经验模态分解算法(Empirical Mode Decompo‐sition，EMD)是近年来出现的一种新型的信号处理方法，是针对非线性非平稳信号的分析方法，已经被广泛的应用于多个领域[3-6]，然而在建筑节能方面的研究确很少[7][8]。针对目前研究的现状，以江苏省南京市民用建筑的墙体实测数据为基础，应用经验模态分解对节能建筑墙体夏季实测温度数据进行分解，分解出系列经验模态函数(Intrinsic Mode Function，IMF)，对其物理含义进行了分析和比较，剔除了测量信号种的随机噪声，筛选出主导模态函数。和传统的傅里叶级数相比，经验模态分解算法阶数少，拟合精度高。该研究为未来建筑围护结构传热分析的数字化、智能化提供了新型高效的分析计算方法。

1 经验模态分解算法

1.1 EMD原理及过程

对任一待分析的原始信号s(t)，首先将其所有极大值点和所有极小值点分别用两条三次样条曲线拟合起来，使两条曲线包含所有信号数据，从而得到s(t)的上、下两条包络线，取上下包络线的平均值为m(t)，则有：[9]

将 h(t)视为新的s(t)，重复(1)式，直到 h(t)满足IMF的两个条件时，此时的h(t)就是原分析信号的第一阶IMF，即c1(t)：

用原分析信号s(t)减去第一阶IMFc1(t)，得到余值序列 r(t)：

将r(t)视为新的s(t)，重复以上过程，可依次得第二阶 IMFc2(t)，第三阶 IMFc3(t)，……，直至r(t)变成了一个单调序列，EMD分解结束，得到n阶IMF。把分解出来的n阶IMF和残差r(t)叠加起来，就得到了原序列：

1.2 IMF判断准则的近似方法

对于不同的数据序列，满足以下两个条件的h(t)才是IMF。①对于一个数据序列，极值点个数和过零点的个数必须相等或最多相差一个；②在任意数据点处，由极大值点插值而成的上包络线和极小值点插值而成的下包络线两者平均值为零。

在EMD实际分解过程中，第二个条件很难满足，一般取近似条件，如式(5)，此数值控制在 0.2～0.3 之间[6]：

式中hk-1(t)——第k次分解前的数据序列；hk(t)——第k次分解后的数据序列；T0——采样时间总数。

1.3 IMF筛选的关键技术

每阶IMF都是一个具有特定幅值和频率的时变振荡模式，另外，各个IMF之间近似是正交的，第一阶IMF主要由信号中具有最高频率的成份组成，各阶IMF频率随阶数的上升而下降。

根据信号谱分析的Parseval定理[10][11]，得到各阶IMF能量定义：

式中xi，t——第i个IMF的第t个采样点值。利用能量谱计算模块进行计算后，按照数值大小自动遴选出能量谱的序列，其总和为信号的总能量：

对能量排序居前的IMF作为主导模态信号进行分析。

2 EMD在室外计算逐时综合温度谐波分析中的运用

2.1 原始信号的构成

建筑墙体外表面和室外空气之间对流换热，太阳辐射也向墙体传热，将两者的共同作用温度用空气调节室外计算逐时综合温度来表示[1]。在求解通过围护结构传热量时，无论是理论分析和数值计算，此综合温度是必需的基本参数。

在 2017年 7月 23日 23：00：00～7月 27日22：59：00使用建筑围护结构热工性能现场检测仪，测量得到南京市江宁区某小区11层小高层5楼建筑东墙面实时温度，采样时间间隔1 min。为了消除室内温度波动影响，测量期间室内空气温度保持在21°C左右。测量数据曲线见图1所示。为了比较研究EMD在东、西两个方向室外计算逐时综合温度谐波中的应用，选取了2016年7月18日 23：00：00～7 月 22 日 22：59：00 期间在南京市金陵科技学院图书馆会议室西墙外测量得到的墙面实时温度，采样时间间隔1 min，测量数据曲线见图2所示。测量期间室内空调开启，空气温度保持在23°C左右。

从图1可知，由于天气的变化，在测试周期的最后两天温度有所下降，温度中枢下移。而图2显示，测试周期的后两天，受天气影响，温度总体上升，这些都增加了实测温度研究的复杂性。

图1 小高层建筑东墙夏季实测温度曲线图

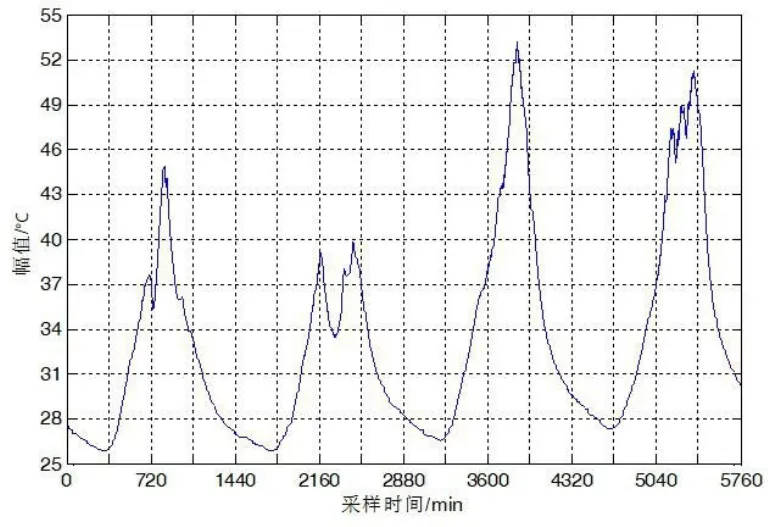
图2 图书馆西墙夏季实测温度曲线图

2.2 原始信号的经验模态分解

对原始信号进行经验模态分解，得到东向、西向实测温度波的各阶经验模态函数如图3、图4所示。

图3 小高层建筑东墙原始信号的经验模态分解

图4 图书馆西墙原始信号的经验模态分解

从总体看，温度变化是以24小时为一个周期，属于典型的低频振荡信号。从所分解的IMF1～IMF3可看出，由于天空云量、空气风速及测量仪器自身性能波动，有大量的噪声影响，活动频率集中出现在白天温度峰值时段，最高不超过0.5 HZ。

从信号的模态函数分解可知，共分解出9阶IMF和1项残差。1～4阶IMF代表所测信号中的噪声分量，具有波动幅值小、发生频率高的特点，各阶IMF幅值均在1左右，故1～4阶噪声影响可忽略不计。从5阶IMF起，IMF开始有显著的周期性的变化，这说明模态函数的主要成分开始反映温度的波动性质，特别是第8阶IMF，具有完全对称分布的波动性质，波幅值基本保持一个常数，该阶IMF即代表了墙外表面室外计算逐时综合温度谐波的主要组成部分，能反映出室外计算逐时综合温度谐波幅值大小、峰值的时间定位及每个周期的温度差异。如2016年7月21日受天气影响，图书馆西墙温度明显降低，相应的在图4中第8阶IMF中的波峰也被明显削平。同样小高层建筑东墙面的第8阶IMF的第三个波动，幅度明显小于其它的温度波形，这准确反映出26日当天室外气温稍低的情况。

残差即相当于傅里叶级数分解当中的常数项，但其是时变的，能很好地反映出温度信号整体的变化趋势。从图3显示分解后的残差项是单调上升曲线，反映了温度整体随天气变化逐渐抬升的变化规律。从图4显示分解后的残差项具有一个极值点，反映了25日的全天温度相对偏高的变化特点。

3 经验模态函数性能解析

3.1 主导IMF的筛选、验证及误差分析

按前述公式(7)，计算出小高层建筑东墙信号序列各阶IMF能量，各阶IMF能量由大到小依次为 IMF8、IMF7、IMF6、IMF9、IMF5、IMF4、IMF3、IMF2、IMF1。 第 5～9 阶 IMF 占 总 能 量 的99.92%，第6～9阶IMF占能量的99.50%，计算分布如图5所示。计算出图书馆西墙信号序列各阶IMF能量，各阶IMF能量由大到小依次为IMF8、IMF9、IMF7、IMF6、IMF5、IMF4、IMF3、IMF2、IMF1。第5～9阶IMF占总能量的99.97%，第6～9阶IMF占能量的99.37%，计算分布如图6所示。

图5 小高层建筑东墙各阶IMF能量统计

图6 图书馆西墙各阶IMF能量统计

分别将小高层建筑东墙和图书馆西墙IMF叠加，的叠加后与原始信号比较图分别如7和8所示。从图7a和8a可知，第6～9阶IMF已能较好的拟合原始信号的主体部分，但在每日极小值处有一定偏差，未能拟合出每日温度的极小值点。从图7b和8b可知，第5～9阶IMF拟合原始信号，在每日极小值点已经有很大的改善，拟合信号极小值基本与原始信号重合。

图7a 小高层东墙第6～9阶IMF和残差叠加与原始信号比较图

图7b 小高层东墙第5～9阶IMF和残差叠加与原始信号比较图

图8a 图书馆西墙第6～9阶IMF和残差叠加与原始信号比较图

图8b 图书馆西墙第5～9阶IMF和残差叠加与原始信号比较图

各阶IMF叠加与原始信号的平均绝对误差(Mean Absolute Error，MAE)见下表 1，故选择第 5～9阶IMF为主导模态函数。

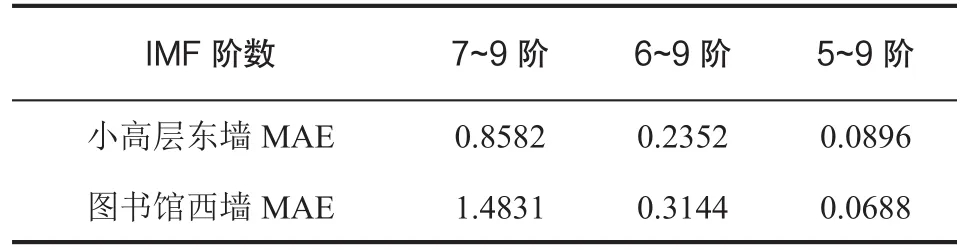
表1 IMF叠加与原始信号的MAE

3.2 主导IMF与傅里叶级数的拟合效果对比

在暖通空调领域，与周期性传热相关的温度谐波和热流谐波都是以傅里叶级数为基础进行分析和计算的[12]。因此，该文分别对小高层东墙和图书馆西墙墙体室外计算逐时综合温度实测数据进行傅里叶级数分解，分解出的12阶谐波的幅值和相位角分别如表2、表3所示。

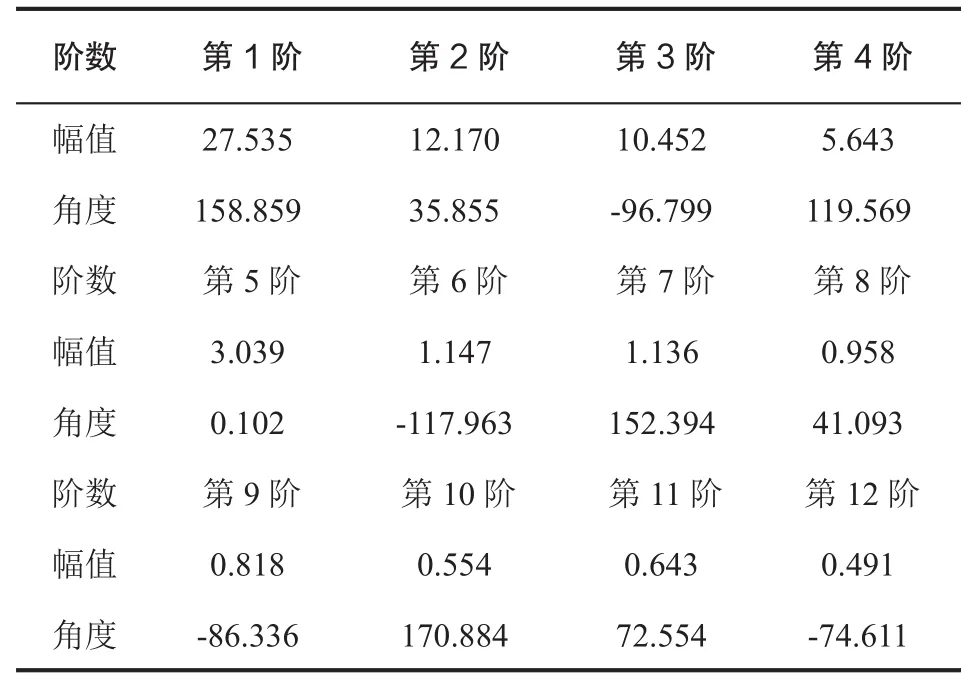
表2 小高层建筑东墙原始信号的傅里叶级数参数

表3 图书馆西墙原始信号的傅里叶级数参数

本文分别将小高层建筑东墙实测数据6阶、12阶傅里叶级数叠加，拟合出温度变化曲线与原始信号比较，结果如图9所示。图10则为对图书馆西墙进行的拟合比较。

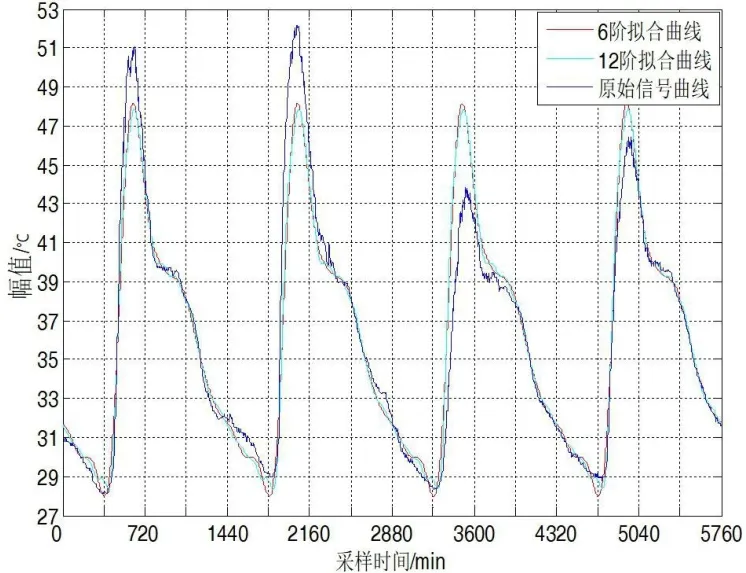
图9 小高层东墙傅里叶级数叠加与原始信号比较图

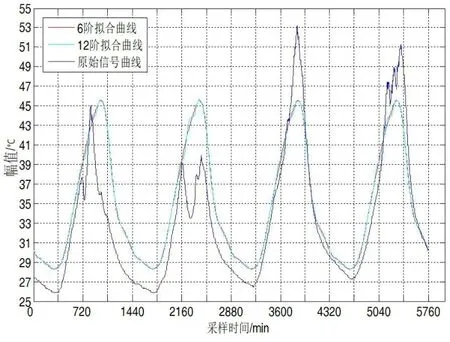
图10 图书馆西墙傅里叶级数叠加与原始信号比较图

因为室外综合温度波随着时间变化波动，是非平稳非线性的。而傅里叶级数是指定基函数和指定频率的平稳周期性时变波动。从图中可见，与实测温度波相比，在温度波峰时间段内，傅里叶级数明显低于实测值，在波谷时间段内傅里叶级数拟合值高于实测值。

傅里叶级数叠加与原始信号误差如表4所示，6阶以后，即使增加傅里叶级数，拟合精度也未有大幅提高。

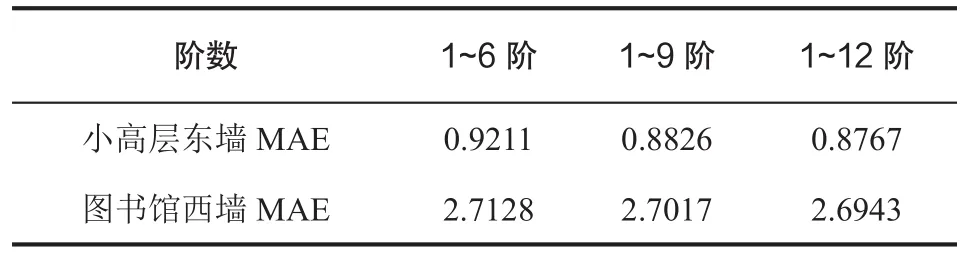
表4 傅里叶级数叠加与原始信号的MAE

与表1相比，主导模态函数拟合精度明显高于傅里叶级数拟合精度。另外，傅里叶级数拟合室外计算逐时综合温度曲线时，不能反映所测时间段内整体偏移趋势，这是因为傅里叶级数在理论上将基频设定为常数。

4 结论

虽然经验模态分解算法起源并大量应用于地震、通讯、机械震动等领域，但对建筑墙体室外综合温度这种非线性非平稳的低频信号也有很好的分析效果，筛选出的主导模态函数与傅里叶级数相比，阶数少、拟合精度高。通过对2个原始测量温度信号样本进行经验模态分解得出实际气候条件下建筑墙体室外综合温度谐波的主导模态函数为第5～9，其中第8阶模态函数能量值占绝对优势，决定了峰、谷数值及相位的位置。该研究为未来建筑围护结构传热分析的数字化、智能化提供了新型高效的分析计算方法。