一种改进光伏发电系统MPPT算法的研究与设计

2019-07-26闫智生

沈阳工程学院学报（自然科学版） 2019年3期

韩刚，闫智生

（1.沈阳工程学院电力学院，辽宁沈阳 110136；2.沈阳农业大学信息与电气工程学院，辽宁沈阳 110866）

在光伏发电系统中，光伏电池是核心部件，其输出功率受到环境中的温度和光照强度影响，光伏电池在工作过程中都存在一个最大的输出功率点。在不同环境下通过相关策略来使得光伏电池始终保持在最大功率输出点，进而提高系统的发电效率，而在最大功率点的搜寻上，通常采用最大功率点追踪法（MPPT，Maximum power point tracking）［1-2］。

1 最大功率点追踪算法研究

1.1 MPPT工作原理

在光伏发电系统中，光伏电池的输出特性除了受到光照强度和温度的影响外，与系统所连接的负载也有直接的关系。当系统所连接的负载不同时，光伏电池对应的输出电压、电流以及功率也随之发生变化。由光伏电池的输出P-U特性可知，在每个输出电压值处都对应着一个功率值，该功率值在最大时必然对应着最大的电压，此时该功率和电压对应的坐标点就是最大功率点。而在外界环境发生变化时，光伏电池的输出特性也在随时发生变化，为了使光伏电池始终保持在最大输出功率点上，必须采用相关的控制方法来对最大功率点进行追踪［3-5］。

1.2 常用MPPT算法分析

1）扰动观察法

在光伏发电系统并网过程中，扰动观察法是一种较为常见的方法。在运行过程中主要通过添加扰动电压ΔU，利用Ppv=Upv*Ipv计算出扰动后相应的光伏阵列输出功率。如果此时计算出的输出功率增加，则表示在该扰动电压的作用下，提高了光伏阵列的输出功率，那么在下一次添加扰动电压时，将会按照相同方向扰动，进而使得光伏阵列输出功率持续增加。如果在扰动电压的作用下，光伏阵列输出的功率降低，那么为了提高光伏阵列的输出功率，在下一次添加扰动电压时将会按照相反的方向进行扰动。这种方法容易控制，在我国早期光伏发电项目中被广泛应用，但是由于这种方法在搜索过程中采用了定步长进行搜索，最后系统的跟踪速度和准确度较低，为此提出了变步长的扰动观察法。在这种方法中，令步长为

式中，A1根据不同的情况进行设置，可以是恒定参数，也可以是变量。

此时的步长可以表示为

由式（1）和（2）可得：

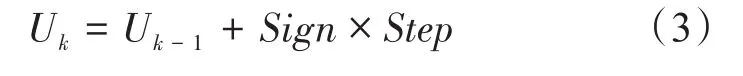
式中，Uk、Uk-1分别表示光伏阵列在此刻和上一刻输出电压值；Step_max表示步长上限值；Step_min表示步长下限值。

图1所示的是扰动观察法原理。假设在k点处光照强度突减，此时a点和b点分别表示k-1和k时刻的工作点，而Uk-1、Uk则表示相应的电压值，Pk-1、Pk是其对应的输出功率值。如果ΔU=Uk-Uk-1＞ 0，ΔP=Pk-Pk-1＞ 0，ΔP/ΔU＞ 0，此时按照扰动观察法基本原理，ΔP＞0将继续按照原来的方向调整，这将导致工作点靠近最大功率点；如果ΔU=Uk-Uk-1＜0，ΔP=Pk-Pk-1＜0，ΔP/ΔU＞ 0，此时按照扰动观察法原理，如果继续施加同方向的扰动电压，即ΔU＜0，这将导致工作点远离最大功率点。

上述分析说明，扰动观察法在运行过程中可能会出现误判的情况，进而导致系统在最大工作点附近来回振荡，使得逆变器的切换损耗增加。

为了验证扰动观察法在运行过程中会出现误判的情况，搭建了相应的仿真模型进行仿真。在仿真过程中，t=8 s时光照强度骤减，此时由图2可以看出扰动方向出现了误判情况，进而导致电压的波动幅度较大，难以快速收敛。图3是在系统误判时的功率曲线，从图中可以看出功率曲线的波动较大，难以快速收敛。

图1 扰动观察法原理

图2 扰动方向误判时光伏电池电压跟踪波形

图3 扰动方向误判时光伏电池输出功率跟踪波形

2）电导增量法

由上述分析可知，扰动观察法在运行过程中会出现误判现象，导致系统在最大功率点附近振荡，影响系统收敛速度，增加了逆变器的切换损耗。为了解决这些问题，有人提出了改进的电导增量法，这种方法采用了梯度变步长来求取电导增量。在这方法中，如果工作点远离了最大功率点后，步长将会变大；相反，如果工作点靠近最大功率点，此时步长将会减小。而步长的符号则可以根据式（4）进行判断，进而在确定了方向后，通过改变步长来实现改变电压变化量ΔU。虽然这种电导增量法相较于传统的方法有了改进，但是在实际的运行过程中还会出现符号误判的情况。图4是k时刻光照强度突然降低导致工作点转移示意图。在k时刻光照强度突然降低，此时光伏阵列的工作点将从a变成b，进而有 dI=Ik-Ik-1，dU=Uk-Uk-1，而b在系统最大功率点的右侧，按照电导增量法原理，此时dI/dU＜-Ik/Uk，但是实际的计算结果是dI/dU＞-Ik/Uk，出现了符号误判的情况。

此外，这种方法在实际计算过程中，并未考虑光照强度突变导致的系统补偿过大情况，这将会导致系统中的电压和功率严重越限，进而导致系统崩溃。为了验证电导增量法在运行过程中会出现误判情况，搭建了相应的仿真模型进行仿真。在仿真过程中，t=8 s时使光照强度突然降低，此时的电压曲线如图5所示，从图中可以看出此时的电压直接跌落为0。图6所示的相应功率曲线也随之跌落为0，系统出现崩溃现象。

图4 k时刻光照强度突然降低工作点转移情况

图5 光照强度骤减系统崩溃时的电压波形

图6 光照强度骤减系统崩溃时的功率波形

2 改进型MPPT算法

为了解决传统的扰动观察法和电导增量法在运行过程中出现的不足，本文提出了一种改进的MPPT算法。MPPT算法的具体流程如图7所示，在搜寻最大功率点时，预先设置一个参考电流Iref，通过拟合分析，设置Iref为光伏阵列峰值电流的一半，此时如果环境中的光照强度没有发生变化，即dI＜Iref，则使用变步长的扰动观察法来搜索最大功率点；如果环境中的光照强度发生变化，即dI＞Iref，则对突变前的符号进行判断，并计算出突变后步长的符号，再利用变步长的扰动观察法来设置步长的上限值和下限值。

利用改进的MPPT算法进行控制时，在光照强度由1 000 W/m2突降到800 W/m2时的电压变化波形和功率变化波形如图8、图9所示。从图8中可以看出，此时在环境快速变化时电压的波动较小，并且拥有更快的跟踪速度。从图9中可以看出，此时在环境快速变化时可以快速跟踪最大功率，同时能够快速收敛。